D. A Simple Task
题目: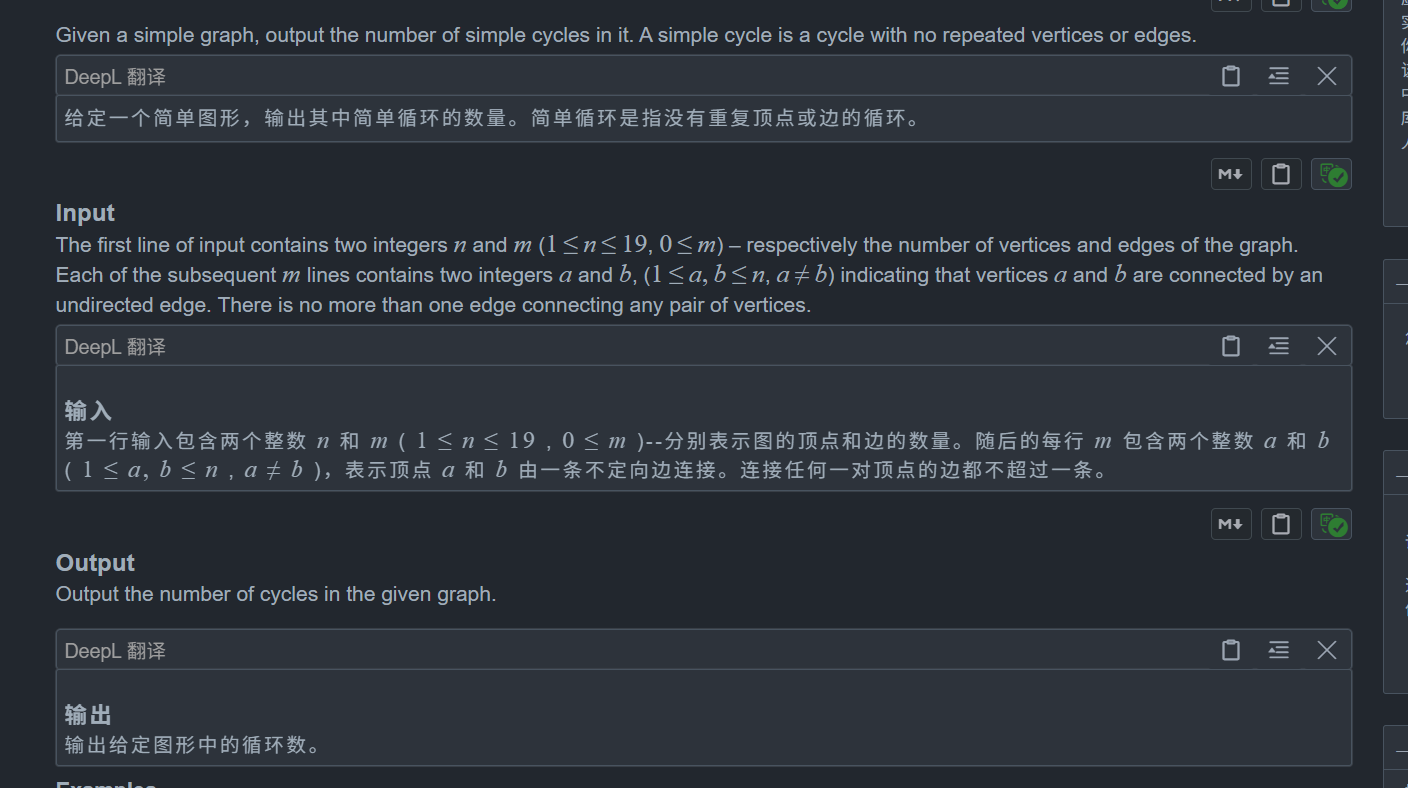
思路:
没想到图也能结合状压DP
本题注意到题目的数据给的很小,n 只有 19,所以不妨考虑状态压缩
我们如果要找到环的话,那么我们需要知道什么呢?一个是走了哪些点,一个是初始点,一个是末尾点
我们分析一下如果我们要找到环,那么肯定就是末尾点等于初始点,所以我们可以定义一个dp,就是 f[i][j] 表示当前状态为 i,终点为 j 的方案数,由于还要知道起始点,这里我们直接将 i 也利用上,最后定义变为:当前状态为 i,且起始点是 i 的最低位,终点为 j 的方案数
对于初始化,显然我们以 j 为起点,状态只走过 j 的方案数都是 1
那么转移也很简单了,看代码即可
特别要注意的就是最后的答案了,我们求出来的答案其实包含了二元环,即每条边,同时由于这个图是无向的,所以我们还需要除以二,因为每条边都可以回走一次,即走两遍
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
int n, m;
//状态为 i,且终点为 j 的方案数,其中 i 的最低位为出发点
int f[1 << 20][20];
vector<vector<int>> g(20);
int ans = 0;
int lowbit(int x)
{
return x & (-x);
}
void solve()
{
cin >> n >> m;
for (int i = 0; i < m; i++)
{
int u, v;
cin >> u >> v;
u--, v--;
g[u].push_back(v);
g[v].push_back(u);
}
for (int i = 0; i < n; i++)
{
f[1 << i][i] = 1;//初始化
}
for (int state = 1; state < 1 << n; state++)
{
for (int i = 0; i < n; i++)
{
//跳过非法状态
if(!f[state][i]) continue;
for(auto & son : g[i])
{
int son_w = 1 << son;
//如果下一个走到点比起始值小的话,那么显然不行,这样就不符合定义了
if(lowbit(state) > son_w)
{
continue;
}
//如果之前走过
if(state & son_w)
{
//并且还是出发点
if(lowbit(state) == son_w)
{
//累加答案
ans += f[state][i];
}
}
else
{
//否则转移
f[state | son_w][son] += f[state][i];
}
}
}
}
// 删除二元环,同时由于无向图同一条边会走两边,所以还要除以 2
cout << (ans - m) / 2 << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
while (t--)
{
solve();
}
return 0;
}C. Almost All Multiples
题目:
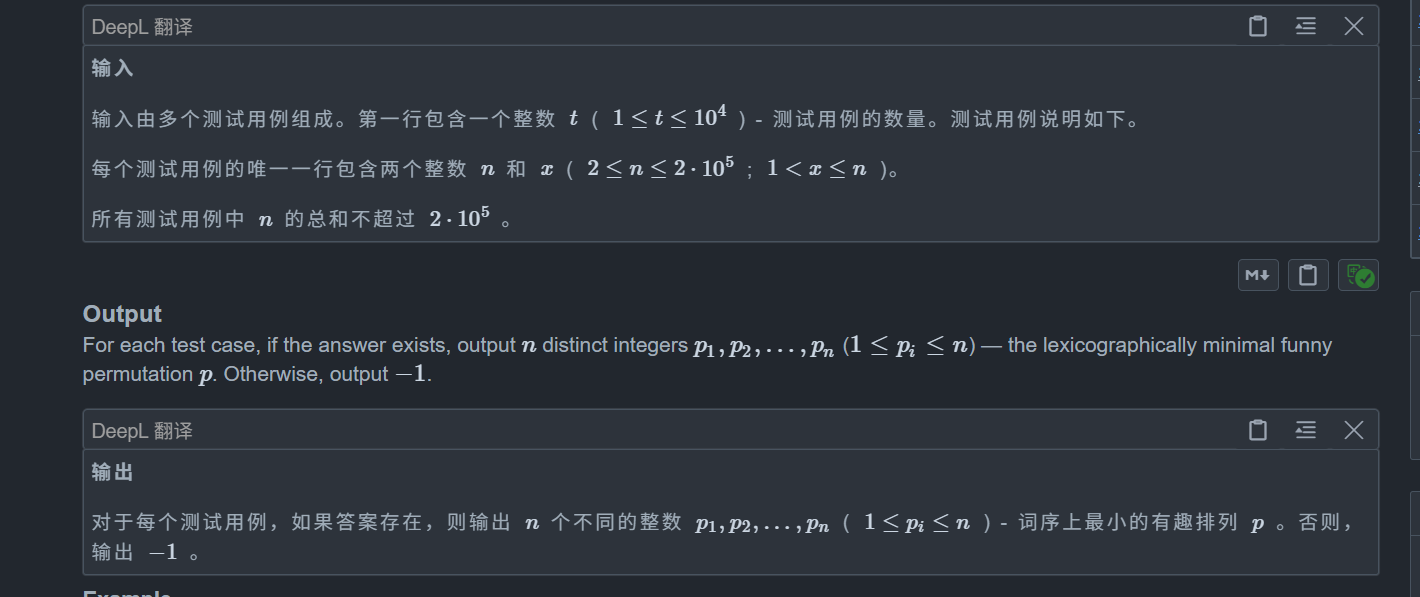 思路:
思路:
本题关键点在于找到无解的性质,同时推出之后的条件
我们先来看看什么情况下无解好了,首先如果我们选走了 x,那么原来的 p[x] = x 的位置就会空出来,所以说就有以下情况:假如我们一共有 c 个 x 的倍数,那么就说明有 c 个位置是给我们填的,但是由于现在我们 p[x] = x 的位置空了,且 c 的倍数少了一个,那么现在就变成了 c-1 个 x 的倍数去填 c 个位置了,同时 p[n] = 1,即 p[n] 这个位置可以不考虑,那么显然我们可以往这方面想,如果 n 是 x 的倍数,那么显然现在 p[n] 位置没了,而 x 没了,那么显然就刚好平衡了
所以结论就是:当 x 不是 n 的因数时无解
随后考虑构造,显然要字典序最小,那么我们就可以每个 p[i] = i,而 p[x] = n 即可
但是某些情况下是无法通过的,为什么呢?因为我们可以将 n 往后移动,这样显然更优,那么什么时候可以将 n 往后移动呢?
如果在 x 后头存在一个位置 p[i],其数字满足 p[i] % x == 0,说明这个数是 x 的倍数,即 i 能放在 p[x] 位置,满足 i = k*x,同时不要忘了,如果 n % i 不等于 0 的话,那么也是不行的,因为我们其实是在将 n 往后移动,如果这个 i 都不是 n 的因子,那么 n 放到 p[i] 上显然是不满足 n = k*i 的
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
void solve()
{
int n, x;
cin >> n >> x;
// 如果 x 不是是 n 的因数,那么无解
if (n % x != 0)
{
cout << "-1\n";
return;
}
vector<int> p(n + 1);
p[1] = x, p[x] = n, p[n] = 1;
for (int i = 2; i < n; i++)
{
if (i != x)
p[i] = i;
}
for (int i = x + 1; i < n; i++)
{
if (!(p[i] % x) && !(n % i))
{
swap(p[i], p[x]);
x = i;
}
}
for (int i = 1; i <= n; i++)
{
cout << p[i] << " ";
}
cout << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}A2. Make Nonzero Sum (hard version)
题目:
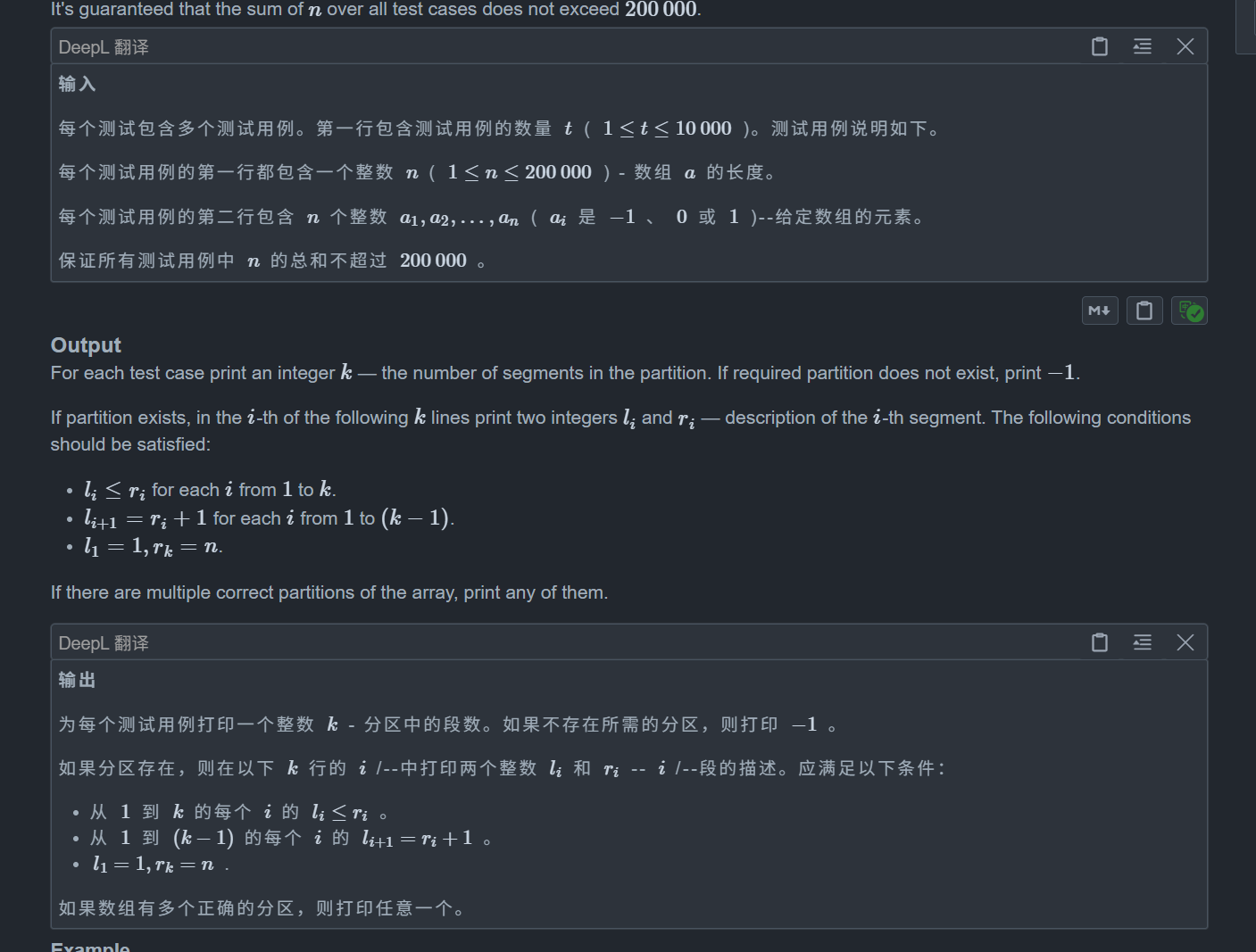 思路:
思路:
没想到直接贪,不过感觉好像做过这种直接贪的题目
我们不难发现一个性质,就是我们每次改变显然都是缩减 2,如 -1 如果变成了 1,那么 -1 的数量减一,而 1 的数量加一,此时二者数量差距显然就增加了 2
所以我们其实可以根据二者初始差距来判断是否有解,但是可以不判断
我们直接模拟过程,我们可以发现其实这个过程相当于在 i 处插上标记,同时不能连续插标记,插上标记的数就相当于添加了负号
所以我们直接贪心,如果当前数插上标记后会缩小二者差距,那么就插,否则不插
贪心也很好证明:如果当前不插,那么就算到后面再插也是改变 2,所以不如提前插
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
void solve()
{
int n;
cin >> n;
vector<int> a(n);
int sum = 0;
int cnt = n;
for (int i = 0; i < n; i++)
{
cin >> a[i];
sum += a[i];
}
vector<int> pass(n+1, 0);
for (int i = 1; i < n; i++)
{
if (abs(sum - 2 * a[i]) < abs(sum) && !pass[i - 1])
{
pass[i] = 1;
cnt--;
sum -= 2 * a[i];
}
}
if (sum)
{
cout << "-1\n";
}
else
{
cout << cnt << endl;
for (int i = 0; i < n; i++)
{
if (pass[i])
continue;
if (pass[i + 1])
{
cout << i+1 << " " << i + 2 << endl;
}
else
{
cout << i + 1 << " " << i + 1 << endl;
}
}
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}C. Complementary XOR
题目:

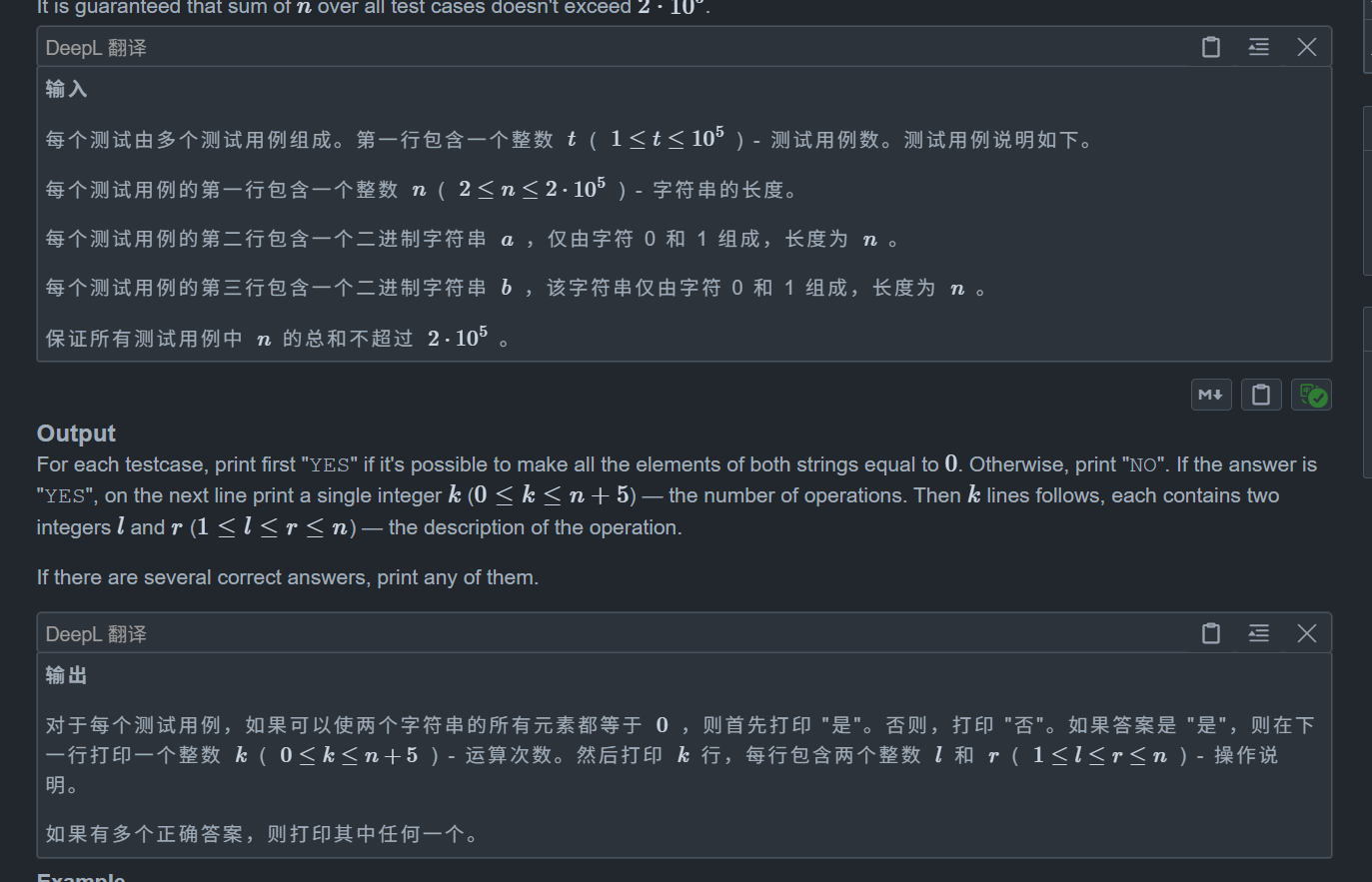 思路:
思路:
题目标题其实给出来了提示
本题关键是找出无解条件,剩下手完一下即可
我们发现题目的条件相当于将 a 的 [l,r] 异或上 1,而 b 的其余地方异或上 1,那么我们结合一下,对于 c = a ^ b,其实就相当于将 c 的所有位异或上了 1,而如果 a b 都为 0,那么就是 c = 0
所以有解的条件就是 a ^ b = 00000.... 或者 a ^ b = 11111...
即所有的 a[i] = b[i] 或所有的 a[i] != b[i]
然后模拟即可,手玩一下可以发现我们只需要将 a[i] = 1 的操作一下即可,最后的局面一定是
00000 111111 或 111111 111111
特判一下即可
代码:
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define yes cout << "YES\n"
#define no cout << "NO\n"
mt19937 rnd(chrono::steady_clock::now().time_since_epoch().count());
void solve()
{
int n;
cin >> n;
string a, b;
cin >> a >> b;
vector<int> cnta(2, 0), cntb(2, 0);
int flag = 0, flag2 = 0;
for (int i = 0; i < n; i++)
{
cnta[a[i] - '0']++;
cntb[b[i] - '0']++;
if (a[i] == b[i])
{
flag = 1;
}
else
{
flag2 = 1;
}
}
if (flag && flag2)
{
no;
return;
}
if (cnta[0] == n && cntb[0] == n)
{
yes;
cout << "0\n";
return;
}
yes;
vector<pair<int, int>> ans;
for (int i = 0; i < n; i++)
{
if (a[i] == '1')
{
ans.push_back({i + 1, i + 1});
}
}
if ((flag && (ans.size() % 2)) || (flag2 && !(ans.size() % 2)))
{
ans.push_back({1, n});
ans.push_back({1, 1});
ans.push_back({2, n});
}
cout << ans.size() << endl;
for (auto &[l, r] : ans)
{
cout << l << " " << r << endl;
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t = 1;
cin >> t;
while (t--)
{
solve();
}
return 0;
}