文章目录
A.守护者之战

这题题意有点不太清楚,但是答案上应该就是直接判断当任意一个人(无论敌我)生命值降低到 0 以下时,他会立即引爆体内的能量核心。,是否成立,只要有一个1就成立
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
const int N=1e6+6;
int a[N];
int b[N];
signed main()
{
int n,m;
cin>>n>>m;
int x=1;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i]==1)
{
x=0;
}
}
for(int i=1;i<=m;i++)
{
cin>>b[i];
}
if(x)
{
cout<<"NO";
}
else
{
cout<<"YES";
}
return 0;
}E.数字支配
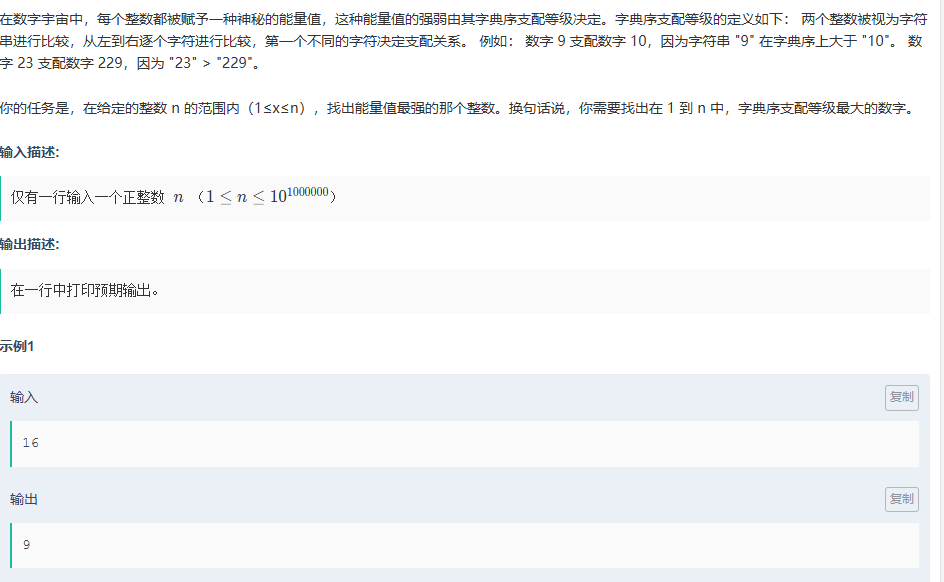
这题就是在1到n内找一个数字使其字典序等级最大,用字符串处理更加简单明了,如果用正常数组的话,可能容易写错
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
signed main()
{
string s;
cin>>s;
if(s.size()==1)
{
cout<<s;
}
else
{
bool vis=1;
for(int i=0;i<s.size()-1;i++)
{
if(s[i]!='9')
{
vis=0;
break;
}
}
if(vis)
{
cout<<s;
}
else
{
for(int i=0;i<s.size()-1;i++)
{
cout<<"9";
}
}
}
return 0;
}I.外卖大战
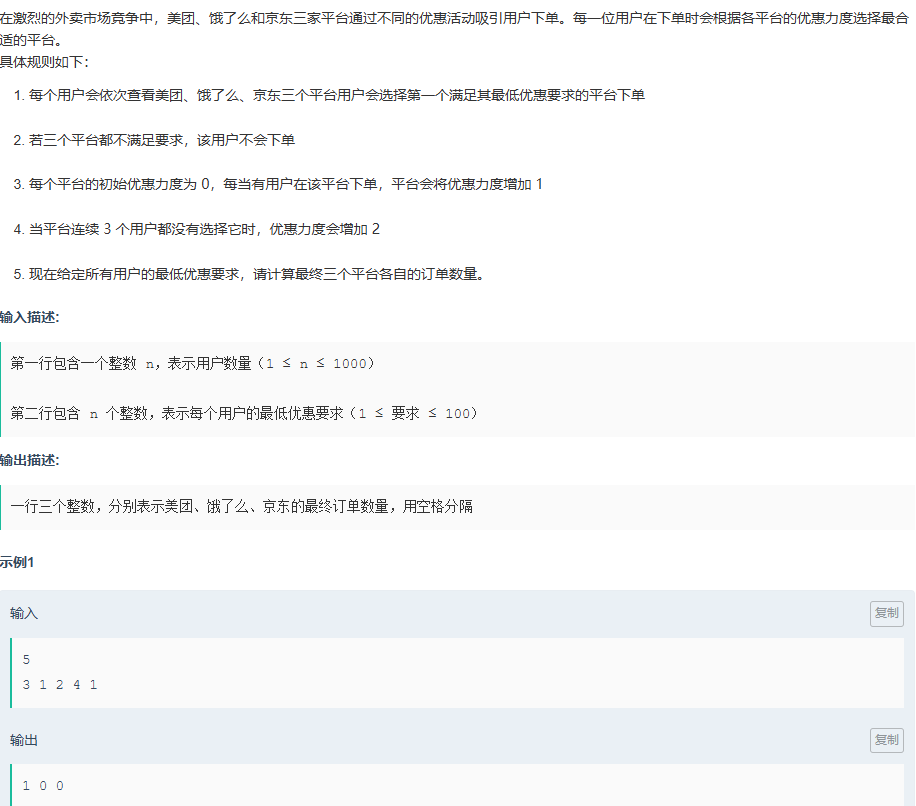
这题就是根据题意模拟就行了
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
int a[1006];//用户
int b[4]={0};//平台优惠力度
int c[4]={0};//模拟第三个规则
int sl[4]={0};//订单数量
signed main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
{
int x=INT_MIN;
for(int j=1;j<=3;j++)
{
if(b[j]>=a[i])
{
b[j]++;
sl[j]++;
c[j]=0;
x=j;
break;
}
}
for(int j=1;j<=3;j++)
{
if(j==x)
{
x=INT_MIN;
continue;
}
else
{
c[j]++;
if(c[j]==3)
{
b[j]+=2;
c[j]=0;
}
}
}
}
for(int i=1;i<=3;i++)
{
cout<<sl[i]<<" ";
}
return 0;
}L.整数商店的购物之旅
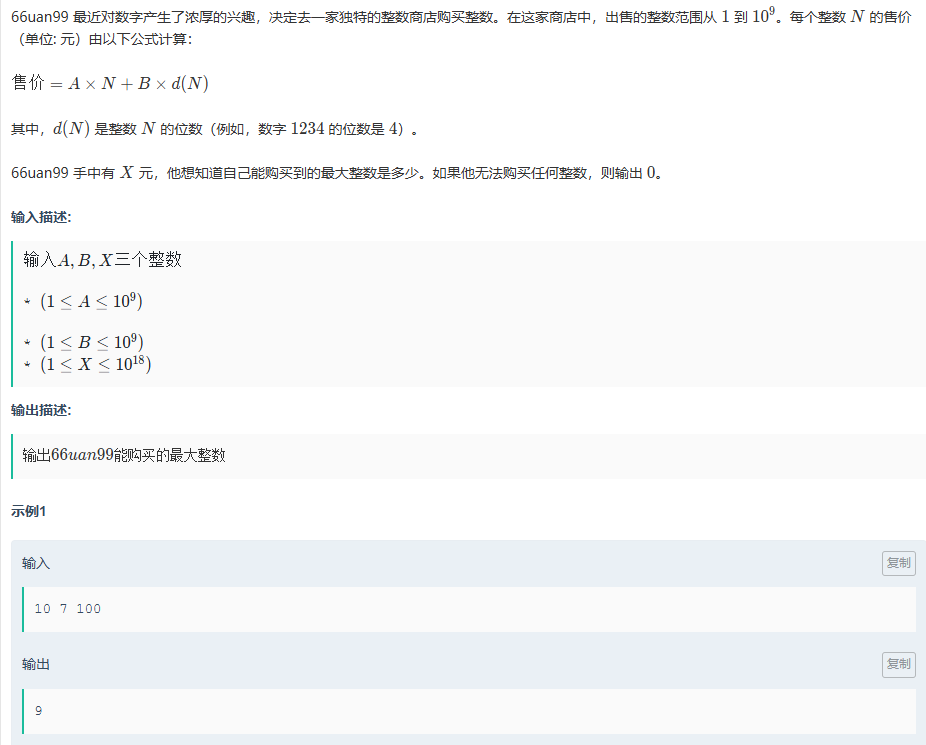
这题其实就是一个简单的二分答案求最大值的题,注意千万不要记错模板,多加1就可能进入死循环
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
int a,b,c;
bool check(int mid)//将mid作为答案代入,看是否符合题意
{
int x=mid;
int y=0;
while(x>0)
{
x=x/10;
y++;
}
int z;
z=a*mid+b*y;
if(z<=c)
{
return true;
}
else
{
return false;
}
}
signed main()
{
cin>>a>>b>>c;
int l=0;
int r=1e9;
int sum;
while(l<r)//模板
{
int mid=(l+r+1)/2;
if(check(mid))
{
l=mid;
sum=l;
}
else
{
r=mid-1;
}
}
cout<<sum;
return 0;
}K.还在分糖果!
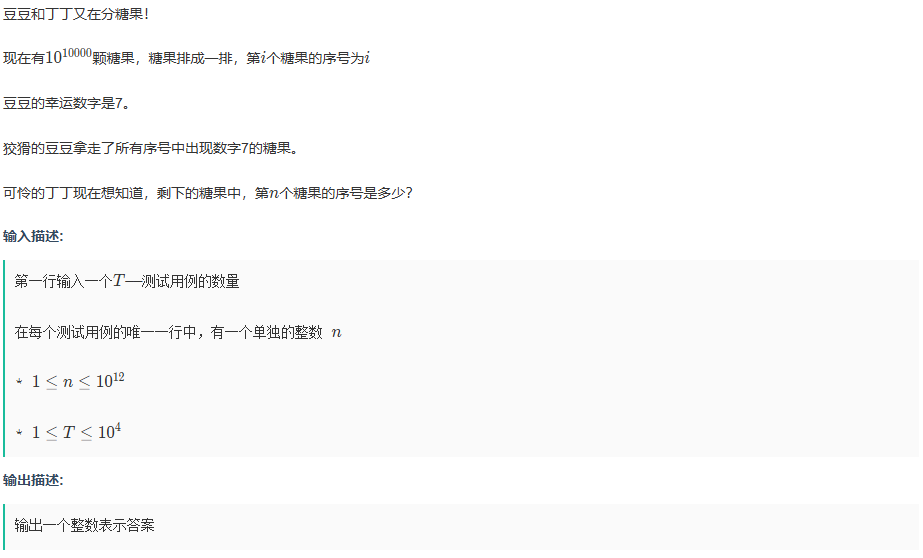

由题意可知,每十个数中就会有一个被去掉,所以可以将n转化为九进制,但是转化后根据样例我们会发现,本来是9变成了8,本来是8变成了7,所以最后要稍作修改
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
signed main()
{
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
int a[15];
int i=0;
vector<int>ve;
while(n>0)//进制转化过程
{
int x=n%9;
if(x>=7)
{
x++;
}
ve.push_back(x);
n=n/9;
}
for(int i=ve.size()-1;i>=0;i--)
{
cout<<ve[i];
}
cout<<endl;
}
return 0;
}D.穿过哈气之门
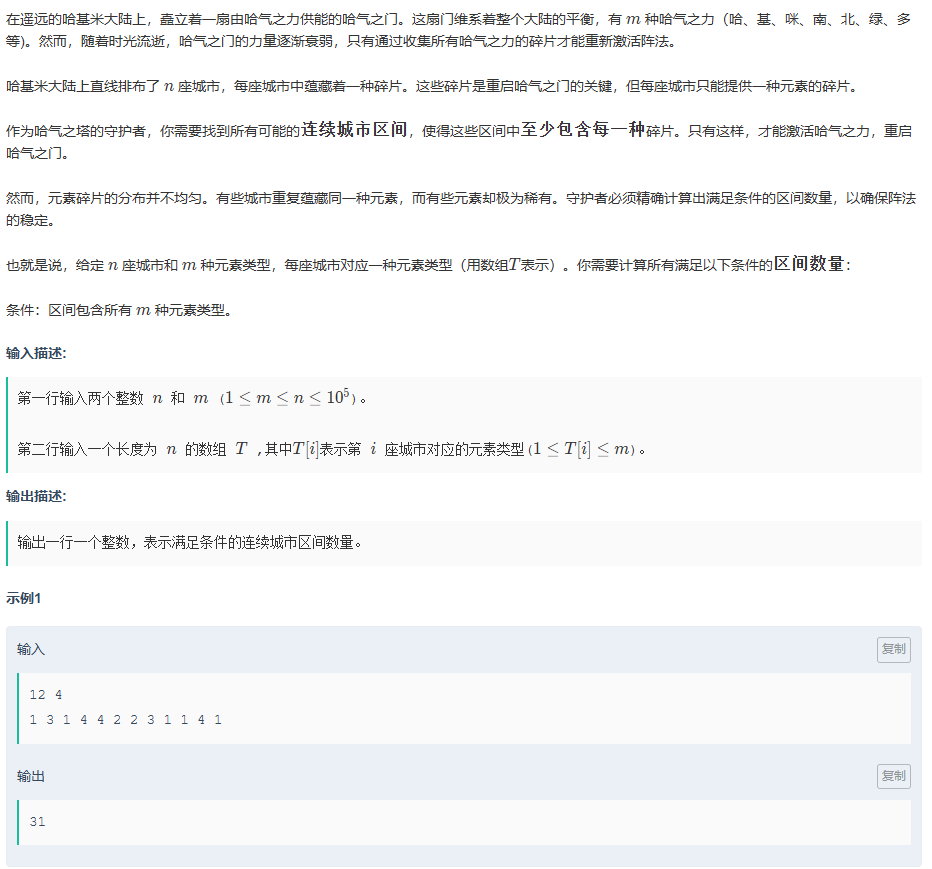
这题题意很明显就是计算每一种包含全部种类元素的区间,对数组我们可以这样操作,遍历数组,每次只从i后面来寻找包含的数组,这样就不会导致所找到全部数组中有重复数组
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
const int N=1e5+6;
int a[N];
signed main()
{
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
map<int,int>mp;
int l=1;//每次从l往后找
int r=0;//记录包含全部种类元素区间的尾节点,那么后面有几个数就是有几种情况(包含区间本身)
int c=0;//记录当前区间内元素种类数
int sum=0;//记录总区间种类数
while(r<n)//限制条件
{
while(r<n&&c<m)//限制条件
{
r++;
if(mp[a[r]]==0)
{
c++;
}
mp[a[r]]++;
}
if(c==m)//一定要注意,如果上面遍历完后c不一定等于m
{
sum+=n-r+1;
while(c==m)
{
mp[a[l]]--;//l不断向右,所以之前经过的节点会出数组
if(mp[a[l]]==0)
{
c--;
}
l++;
if(c!=m)
{
break;
}
sum+=n-r+1;
}
}
else
{
break;
}
}
cout<<sum;
return 0;
}J.凹包
这个之前从来没接触过,也是涨知识了
- 凸包的定义 :
凸包是包含所有原始点的最小凸多边形 ,其顶点一定是原始点的子集 (凸包顶点只能从原始点中选择,不会凭空生成新点)。因此,凸包顶点数 ≤ 原始点数 是必然结论(不可能出现 "凸包顶点数超过原始点数" 的情况,原代码中else分支实际永远不会触发)。- 凸多边形 vs 凹多边形的本质区别 :
- 若一个多边形是凸多边形 :其所有顶点都在自身的凸包上(因为凸多边形的最小凸包就是它本身),此时 "凸包顶点数 = 原始点数"。
- 若一个多边形是凹多边形 :其至少有一个顶点(或内部点)不在自身的凸包上(凹多边形的凸包会 "跳过" 凹陷处的顶点,用更外侧的顶点构成凸边界),此时 "凸包顶点数 < 原始点数"。
判断凹多边形:
1.只有当凸包顶点数 < 原始点数时,才存在点不在凸包上,进而说明是凹多边形。
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
const int N=2e5+6;
pii ve[N];//存储输入的点坐标
pii pa[N]; //存储凸包上的点
bool cmp(pii p,pii q)//对各个坐标排序
{
if(p.fi==q.fi)
{
return p.se<q.se;
}
return p.fi<q.fi;
}
int mc(int x1,int y1,int x2,int y2,int x3,int y3)//叉积计算
{
return x1*y2+x3*y1+x2*y3-x3*y2-x2*y1-x1*y3;
//结果为正:逆时针方向
//结果为负:顺时针方向
//结果为 0:共线
}
signed main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>ve[i].fi>>ve[i].se;
}
if(n==3)//特殊判断
{
cout<<"No";
}
else
{
sort(ve+1,ve+n+1,cmp);
int c=0;
for(int i=1;i<=n;i++)//构建下凸包
{// 当至少有2个点且新点导致凹形时,删除前一个点
while(c>1&&mc(pa[c].fi,pa[c].se,pa[c-1].fi,pa[c-1].se,ve[i].fi,ve[i].se)>0)
{
c--;
}
pa[++c]=ve[i];
}
int d=c;
for(int i=n-1;i>=1;i--)//构建上凸包,这里的n-1是由于
{// 当至少有下凸包+1个点且新点导致凹形时,删除前一个点
while(c>d&&mc(pa[c].fi,pa[c].se,pa[c-1].fi,pa[c-1].se,ve[i].fi,ve[i].se)>0)
{
c--;
}
pa[++c]=ve[i];
}
c--;//起始点会被计入两次
if(c<=n)
{
cout<<"YES";
}
else
{
cout<<"NO";
}
}
return 0;
}2.判断 "按已知顺序(如顺时针 / 逆时针)输入的多边形是否为凹多边形
如果发现任何一个顶点处的转向与其他顶点不一致(出现负的叉积),说明这是凹多边形
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios;;sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
const int N=2e5+6;
pii a[N];
int mc(pii p1, pii p2, pii p3) {//计算叉积
return (p2.fi - p1.fi) * (p3.se - p2.se) - (p2.se - p1.se) * (p3.fi - p2.fi);
}
signed main()
{
int n;
cin>>n;
for(int i=0;i<n;i++)
{
cin>>a[i].fi>>a[i].se;
}
if(n==3)//特殊判断
{
cout<<"No";
}
else
{
int vis=1;//标记作用
for(int i=0;i<n;i++)
{
pii p2=a[(i+1)%n];//取余n是为了最后两个会超出的情况,a[n]就相当于a[0],a[n+1]就相当于a[1]
pii p3=a[(i+2)%n];
if(mc(a[i],p2,p3)<0)//此时其就是一个凹多边形
{
cout<<"Yes";
vis=0;
break;
}
}
if(vis)
{
cout<<"No";
}
}
return 0;
}F.迷宫穿越
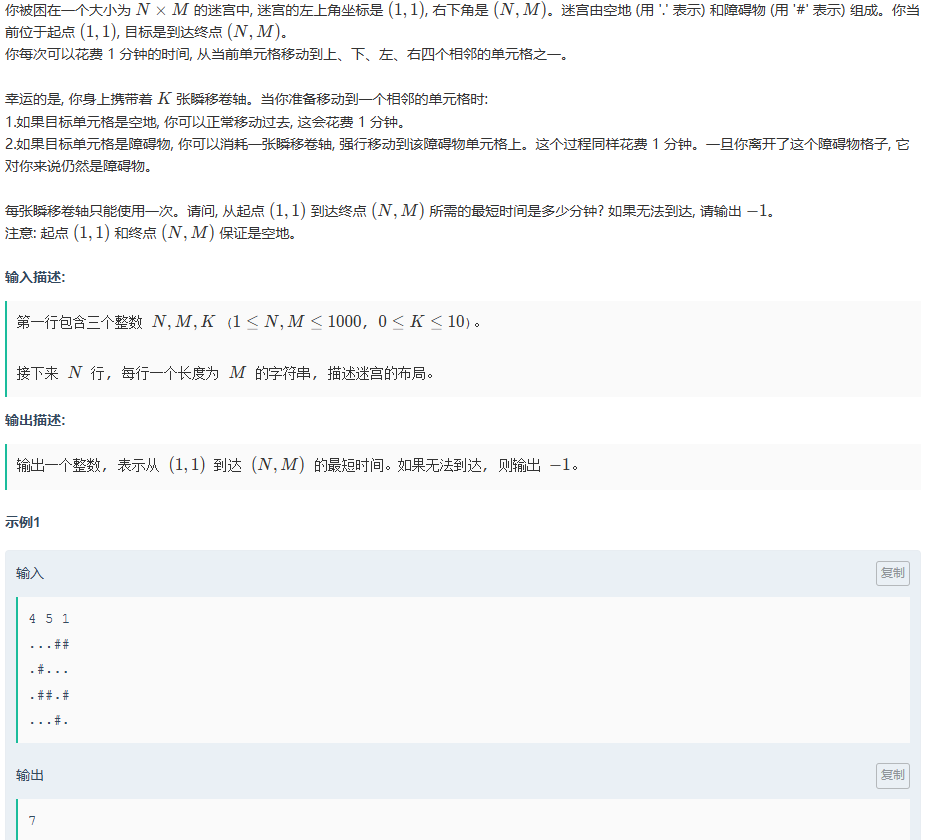
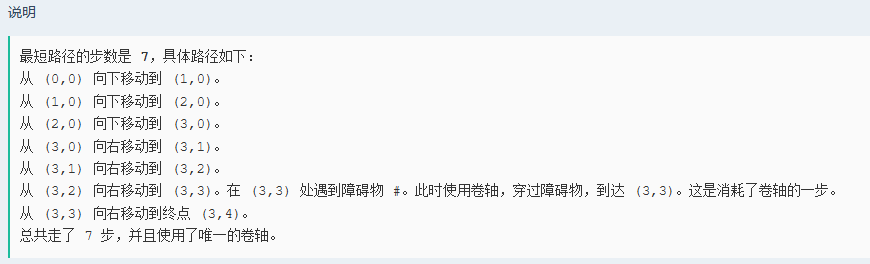
这题虽然题面与其说明不太一样,但是其实就是就从左上角走到右下角的最短路问题,比正常求最短路多了一个可以穿过障碍的条件,此时在写的时候一定要注意,每条路有可能会经过一个相同的点,所以此时要分别记录每个点的各种情况,此时就可以用到一个三维数组,来记录情况
cpp
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define pii pair<int,int>
#define fi first
#define se second
#define int long long
#define endl '\n'
const int INF=0x3f3f3f3f;
char ch[1006][1006];//原数组
bool vis[1006][1006];//标记数组
int d[1006][1006][11];//表示到达(x,y)且剩余k次破坏能力时的最短距离
int dx[]={1,0,-1,0};//四个方向的偏移
int dy[]={0,1,0,-1};
priority_queue<pair<pii,pii>,vector<pair<pii,pii>>,greater<pair<pii,pii>>>pq;
//存储{ {距离, 剩余破坏次数}, {x坐标, y坐标} },由于本人之前写的是用pair二元组,这里可以改成结构体
signed main()
{
int n,m,k;
cin>>n>>m>>k;
memset(vis,0,sizeof(vis));
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
cin>>ch[i][j];
if(ch[i][j]=='#')
{
vis[i][j]=1;
}
}
}
memset(d,INF,sizeof(d));
d[0][0][k]=0;
pq.push({{0,k},{0,0}});
bool bl=1;
while(!pq.empty())
{
pair<pii,pii>x=pq.top();
pq.pop();
if(x.se.fi==n-1&&x.se.se==m-1)//表示到达目标点
{
bl=0;
cout<<x.fi.fi;
break;
}
for(int i=0;i<4;i++)//遍历四种方向情况
{
int x1=x.se.fi+dx[i];
int y1=x.se.se+dy[i];
if(x1>=0&&x1<n&&y1>=0&&y1<m)//表示没有越界
{
if(!vis[x1][y1])//不是障碍物
{
if(d[x1][y1][x.fi.se]>x.fi.fi+1)//比较最短路
{
d[x1][y1][x.fi.se]=x.fi.fi+1;
pq.push({{x.fi.fi+1,x.fi.se},{x1,y1}});
}
}
else//是障碍物
{
if(x.fi.se>0&&d[x1][y1][x.fi.se-1]>x.fi.fi+1)//此时判断是否还有瞬移卷轴与比较最短路
//注意这里是d[x1][y1][x.fi.se-1],而不是d[x1][y1][x.fi.se]
{
d[x1][y1][x.fi.se-1]=x.fi.fi+1;
pq.push({{x.fi.fi+1,x.fi.se-1},{x1,y1}});
}
}
}
}
}
if(bl)
{
cout<<"-1";
}
return 0;
}这题本人写的比较繁杂
如果有错误,烦请指出