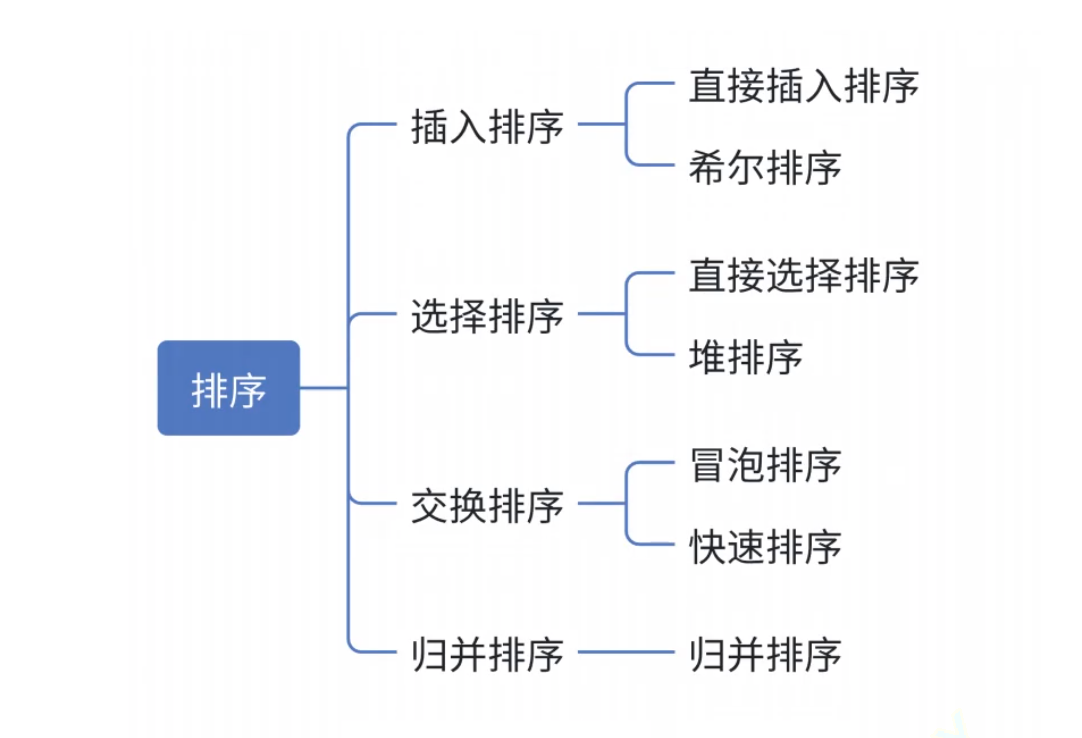
归并排序
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。画图理解归并排序核心步骤:
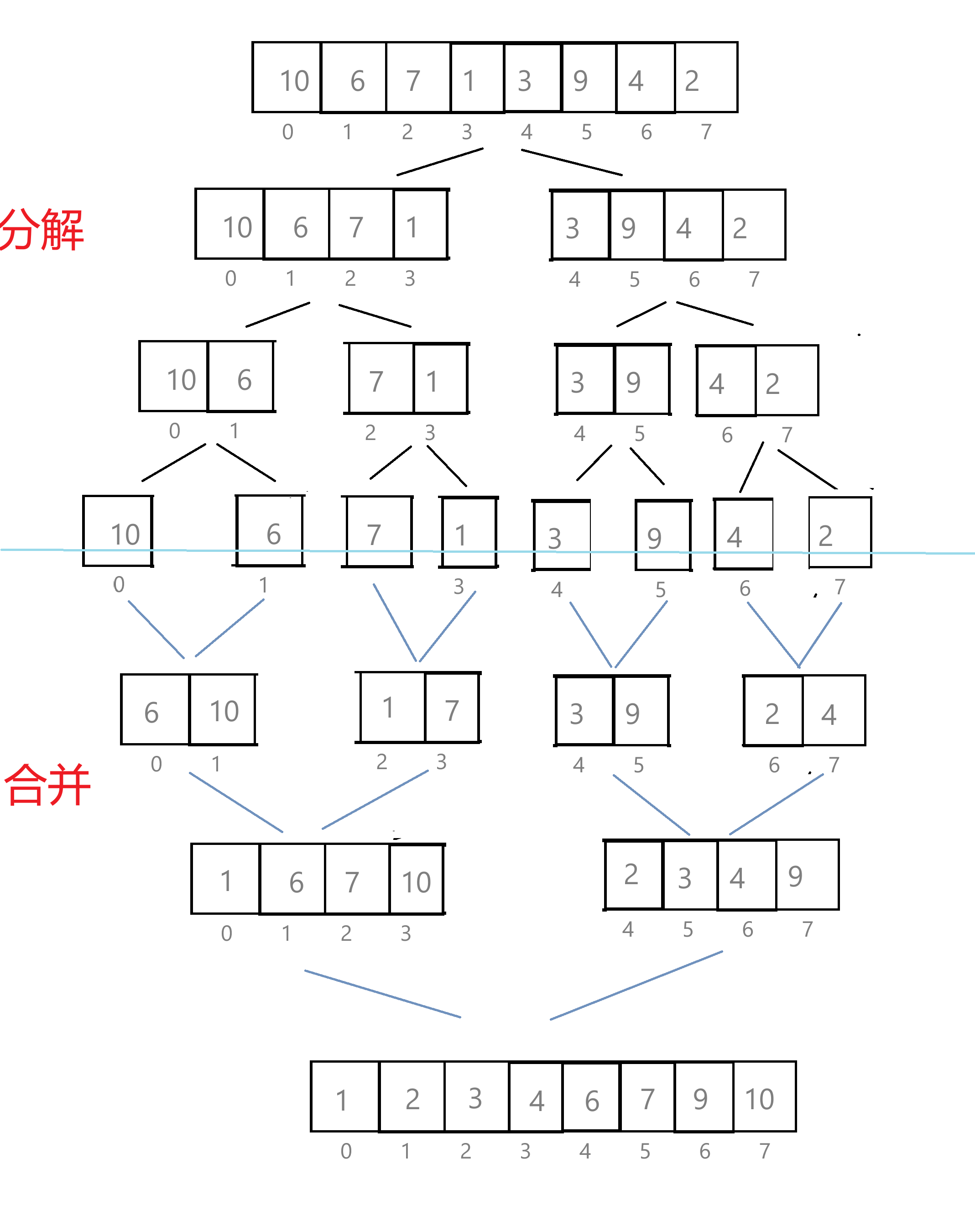
我们先来写一下代码:
void _MergeSort(int* arr, int left, int right, int* tmp)
{
//分解
//if条件:实际上,只会出现left==right的状况,此时表示序列中只含有一个元素,
//之所以写成left>=right可以增强代码的健壮性,你当然也可以直接写成left==right
if (left >= right)
{
return;
}
//如果序列中不止一个元素,那就将它从中间分隔开
int mid = (left + right) / 2;
//所得到的两个序列:[ left ,mid] [mid+1,right]
//继续将左序列和右序列分隔开
_MergeSort(arr, left, mid,tmp);
_MergeSort(arr, mid + 1, right,tmp);
//合并
//定义左序列的起始坐标和末尾坐标
int begin1 = left, end1 = mid;
//定义右序列的起始坐标和末尾坐标
int begin2 = mid + 1, end2 = right;
//定义应该存放在tmp数组中起始位置的坐标
int index = left;
//合并两个序列
while (begin1 <= end1 && begin2 <= end2)
{
//谁小谁就先放到tmp数组中
if (arr[begin1] < arr[begin2])
{
tmp[index++] = arr[begin1++];
}
else
{
tmp[index++] = arr[begin2++];
}
}
//将未放到tmp中的元素循环放入tmp中
while (begin1 <= end1)
{
tmp[index++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = arr[begin2++];
}
//将tmp中的元素放入arr中
for (int i = left; i <=right ; i++)
{
arr[i] = tmp[i];
}
}
//归并排序
void MergeSort(int* arr, int n)
{
//创建一个等大的数组用于存放排好序的序列
int* tmp = (int*)malloc(sizeof(int) * n);
int left = 0, right = n - 1;
_MergeSort(arr, left, right, tmp);
free(tmp);
tmp = NULL;
}可能光看代码和注释还是不太容易理解,小编结合实例来演示一遍,假设我们现在要对数组{10,6,7,1,3,9,4,2}进行排序,在MergeSort函数中,我们创建了数组tmp,大小是8,并将4个参数传给了_MergeSort函数,数组开始了递归之旅。
接下来我们将_MergeSort()函数的栈桢抽象为下图,小编将通过画图来模拟递归过程:

第一次调用_MergeSort()时,left=0,right=7,mid=3,接着就要递归调用_MergeSort()函数分割左序列,如图

于是在第二次递归调用的函数栈桢中,又要递归调用分割左序列的函数:
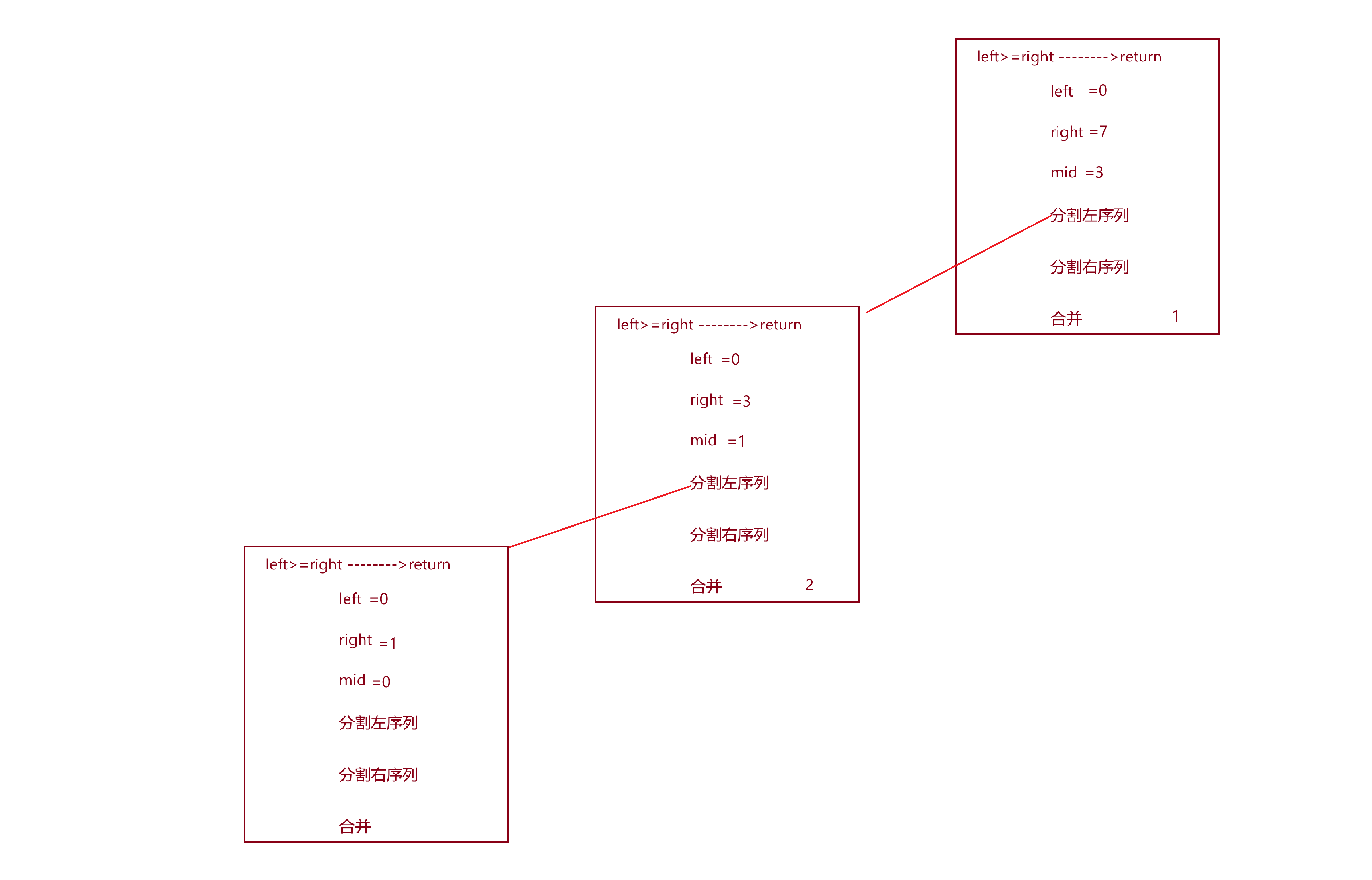
于是又要继续调用分割左序列的函数
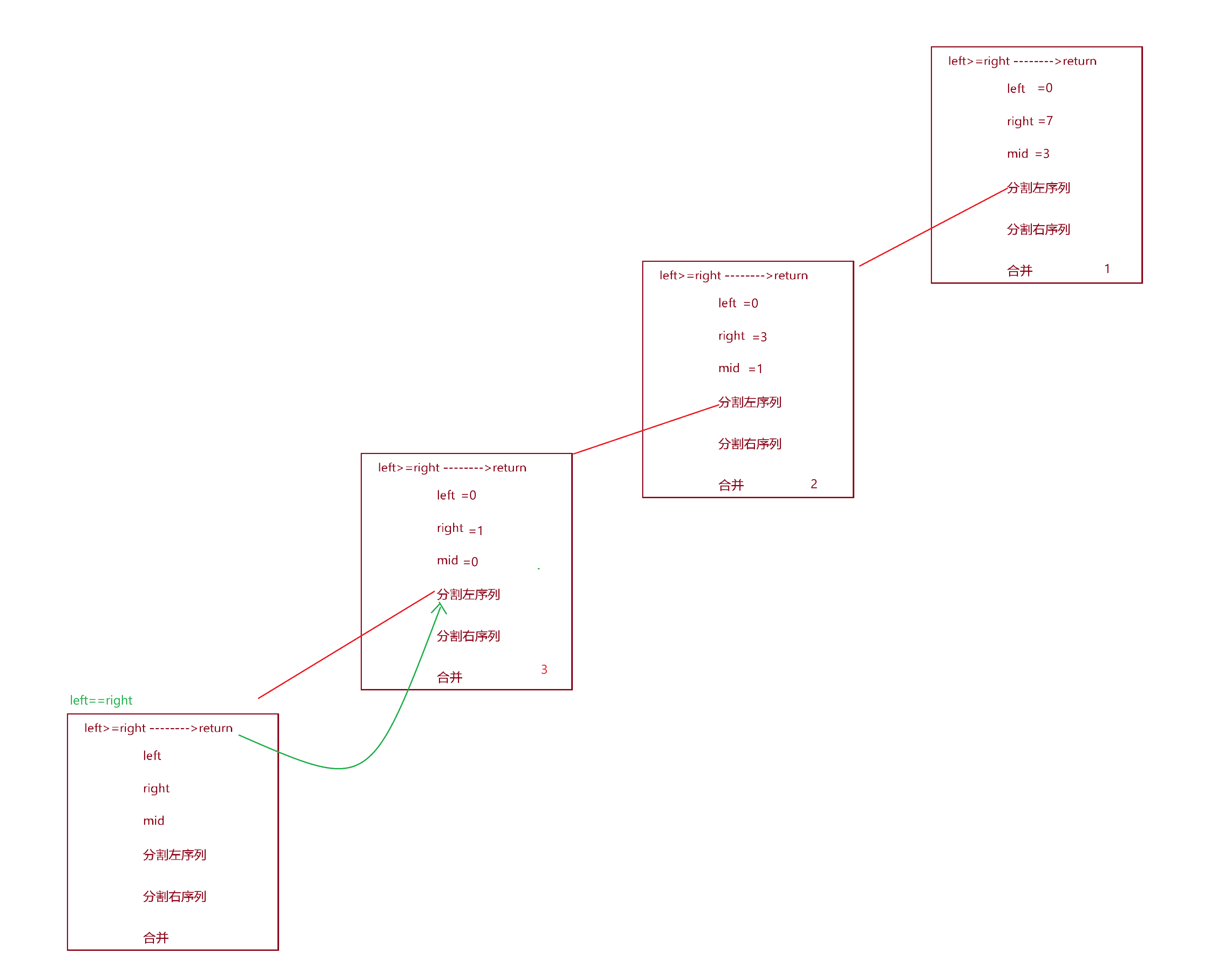
此时由于命中if条件,直接返回。
接下来我们就直接画出所有的递归过程,调用原理与上面的步骤是一样的:
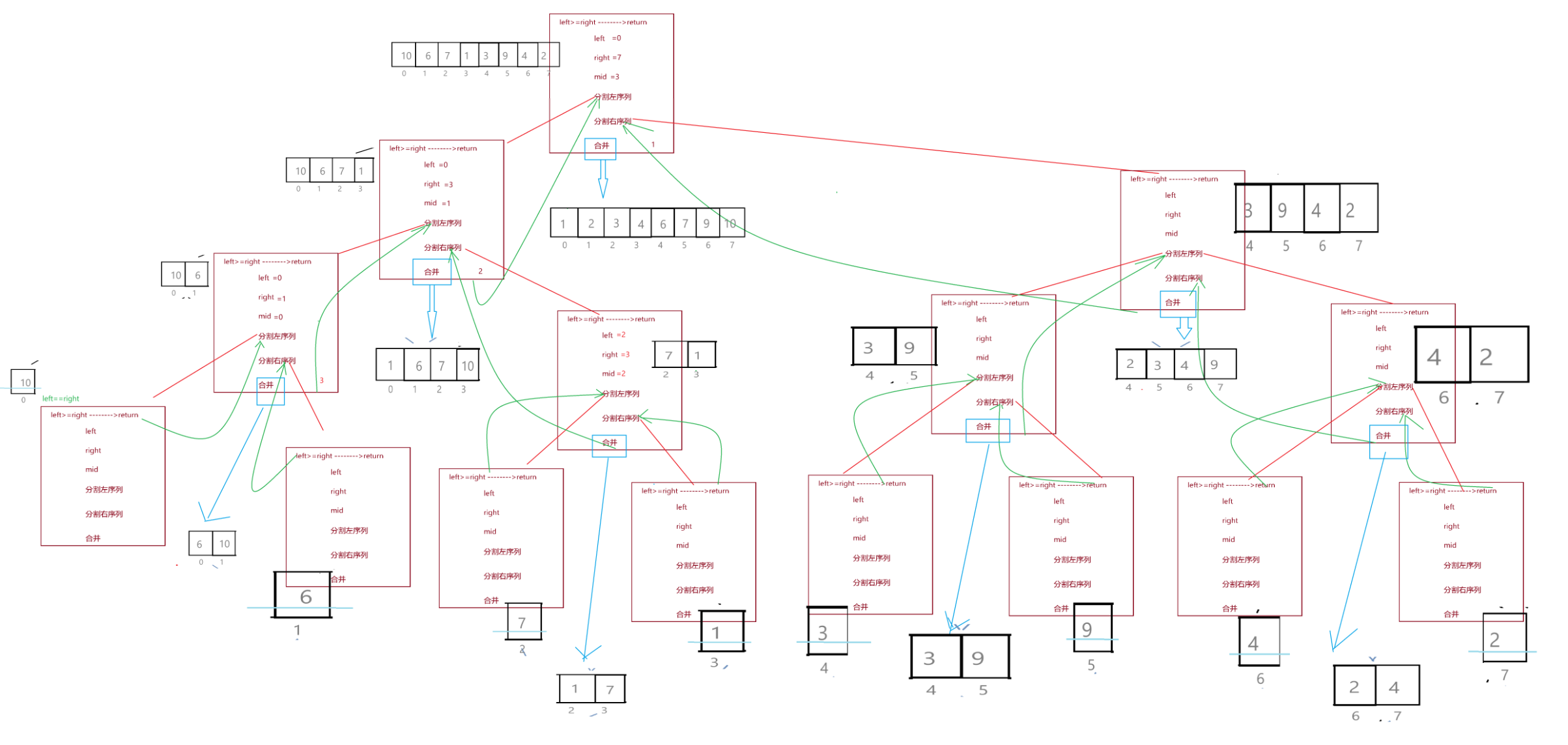
如图就是整个过程中的函数栈桢创建销毁图,红色表示函数栈桢的创建,绿色表示函数返回,返回后函数栈桢要销毁。
合并两个序列的算法是比较简单的,兄弟们简单看一下就好。
时间复杂度分析:
这是一个递归算法,递归算法的时间复杂度=递归次数*单次递归的时间复杂度。单次递归的时间复杂度取决于合并两个序列的那部分代码,合并序列需要我们遍历两个序列,然后将值放到tmp数组中,时间复杂为O(N),递归次数就取决于需要将序列划分多少次,从图中我们可以看到,这是一个二叉树形状的递归过程,所以递归次数就是二叉树的高度logN,所以该算法的时间复杂度就是O(N*logN).
我们在实现算法的过程中额外创建了一个原数组大小的空间,空间复杂度就是O(N)。
非比较排序------计数排序
计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。操作步骤:
1)统计相同元素出现次数
2)根据统计的结果将序列回收到原来的序列中
我们先来简单理解一下计数排序的做法:
假设我们有一个数组{6,1,2,9,4,2,4,1,4},我们先来统计一下每个元素在数组中出现的次数:
|------|------|
| 数组元素 | 出现次数 |
| 6 | 1 |
| 1 | 2 |
| 2 | 2 |
| 9 | 1 |
| 4 | 3 |
我们再来创建一个数组count,arr数组中最大的元素是9,所以我们给定count数组的大小是9+1=10,确保数组的下标范围是在0~9,那么count数组里面的值应该如何给定呢?
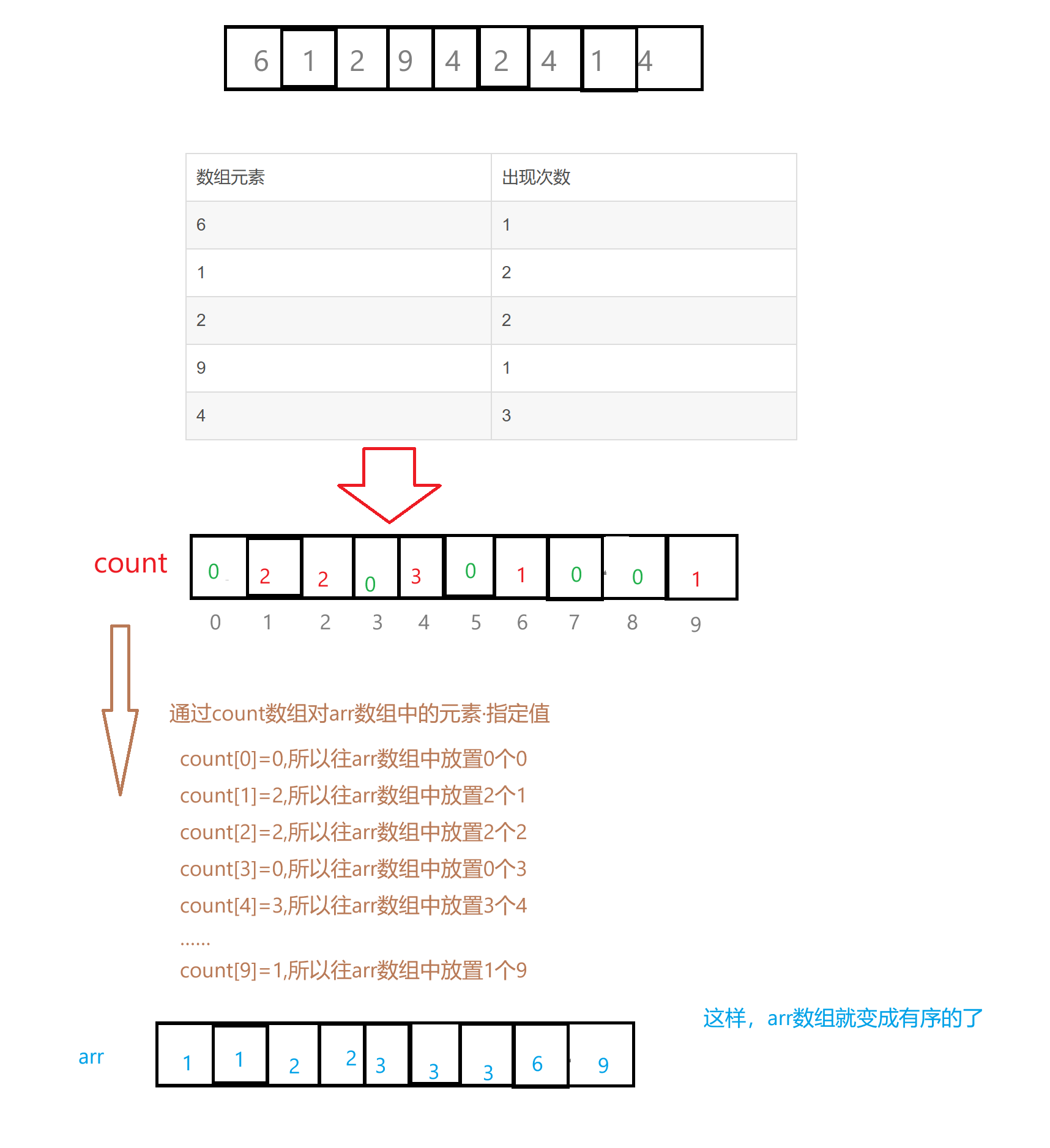
上面我们通过对arr数组中的每个元素统计它们出现的次数,再通过一定的算法将数组排成有序的了,以下为上面排序思想的基本思路:
- 首先统计待排序数组中每个元素出现的次数,构建一个计数数组(如示例中的
count数组),计数数组的下标对应待排序数组中的元素值,数组元素值对应该下标元素出现的次数。 - 然后根据计数数组的统计结果,依次将元素按照出现次数回放到原数组(或新数组)中,从而实现对原数组的排序。通过这种方式,无需进行元素之间的比较,就能完成排序操作。
上面就是计数排序的思想,但是,想一下,如果我们的arr数组中存放的是{101,106,103,106,109,107,104,103},数组中最大的元素是109,难道我们需要给count数组开辟109+1个空间吗?如果是这样的话,按照上面的方法count数组中只有下标为101~109之间的部分位置有非0值,这样会导致空间大大浪费。
我们可以发现,arr数组中的内容集中在101~109,那我们是否可以考虑一种映射方式,将arr数组中的元素通过一种映射变成count数组的下标?
可以的,既然arr数组的元素范围在101~109,我们就只需要创建一个数组,使这个数组的大小为最大值-最小值+1,这样这个数组就能放下101~109间所有数字出现的次数。
那么如何确定count数组下标与arr数组中元素的对应关系呢,我们就以上面的数组为例子:
|-----------|--------------|------------------------|------------------------------|
| arr数组中的元素 | 对应count数组的下标 | 根据count数组的下标i还原arr中的元素 | arr数组中元素的出现次数(count数组对应位置的值) |
| data | data-min | data=i+min | |
| 101 | 101-101=0 | 101 | 1 |
| 106 | 106-101=5 | 106 | 2 |
| 103 | 103-101=2 | 103 | 2 |
| 109 | 109-101=8 | 109 | 1 |
| 104 | 104-101=3 | 104 | 1 |
| 107 | 107-101=6 | 107 | 1 |
这样映射以后,就可以沿用上面的思想对arr数组进行计数排序了:
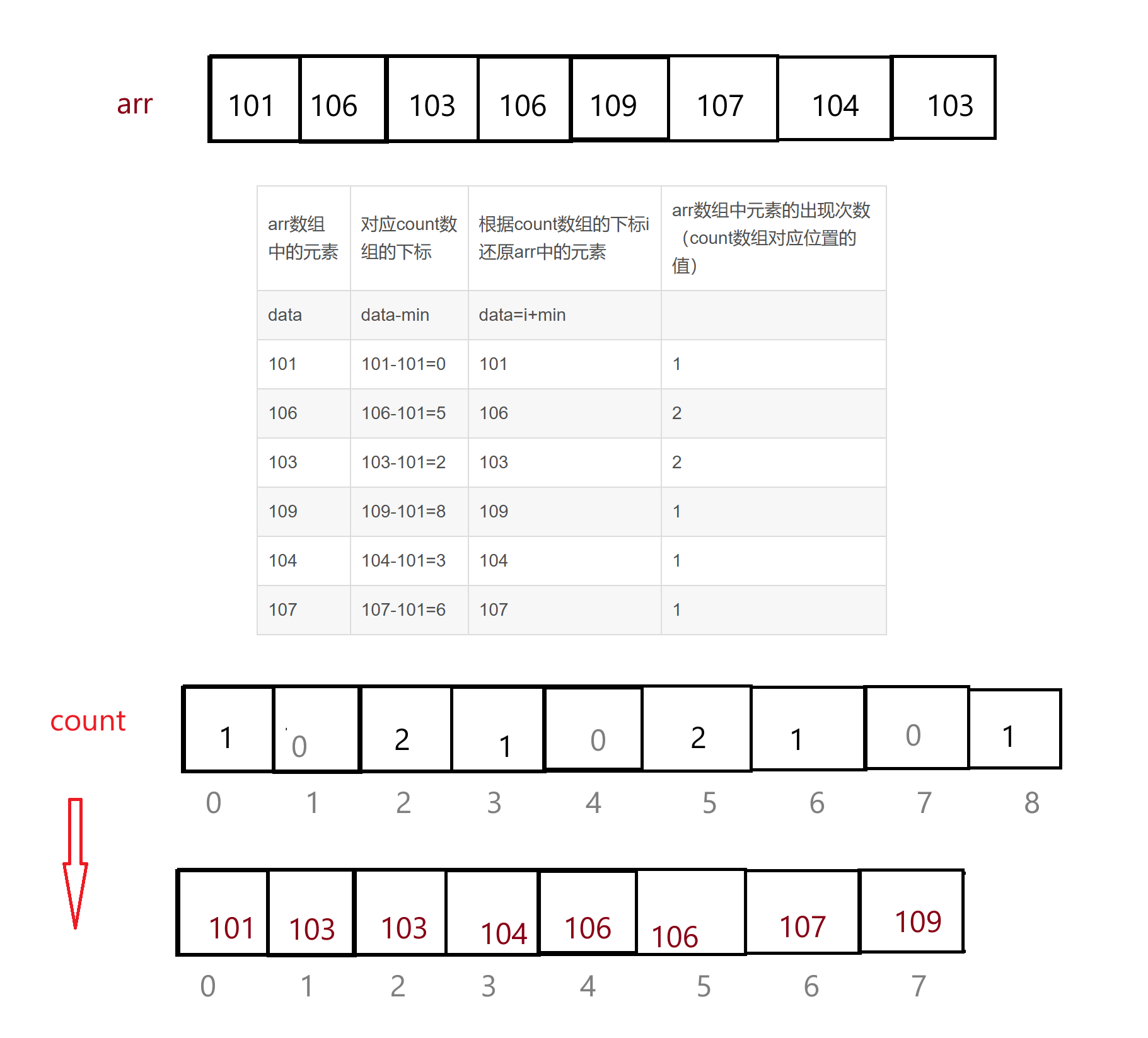
我们再来写一下代码:
//计数排序
#include<stdlib.h>
#include<string.h>
void CountSort(int* arr, int n)
{
//先找到数组中的最小值和最大值,用来计算count数组的大小
int min = arr[0], max = arr[0];
for (int i = 1; i < n; i++)
{
if (arr[i] > max)
{
max = arr[i];
}
if (arr[i] < min)
{
min = arr[i];
}
}
//计算count数组的大小
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range);
//设置count数组中的元素全为0
memset(count, 0, sizeof(int) * range);
//为count数组填充值
for (int i = 0; i < n; i++)
{
count[arr[i] - min]++;
}
//根据count数组为arr数组排序
int index = 0;
for (int i = 0; i < range; i++)
{
while (count[i]--)
{
arr[index++] = i + min;
}
}
}我们可以很容易计算出上面代码的时间复杂度为O(n+range),空间复杂度为O(range)
这样看来计数排序是比较高效的,但是,如果我们要对这样一个数组进行排序{10000,0},难道我们要创建一个大小为10000-0+1的数组吗?如果你要是用计数排序,是这样的,但是这样的话就不太划算了。
所以计数排序也是有它的使用场景的:
计数排序适用场景特征:
-
数据范围小 (值域范围
K不大) -
整数类型(或可映射为整数的数据)
-
数据量较大 (
n远大于K)
小结:本节内容我们讲解了归并排序和计数排序的实现,个人认为归并排序还是比较难以理解的,小伙伴们要好好画一下归并排序的递归调用过程,以便更好地理解代码哦!!
喜欢小编的兄弟们欢迎三连哦,小编会继续更新编程方面的内容的。对于本节内容有任何问题的朋友欢迎在评论区留言哦!!!