【算法精练】 哈夫曼编码

目录

什么是哈夫曼编码？

怎么进行哈夫曼编码？

算法考察

问题一：求编码后的长度

问题二：求各字符编码集合

---

什么是哈夫曼编码？

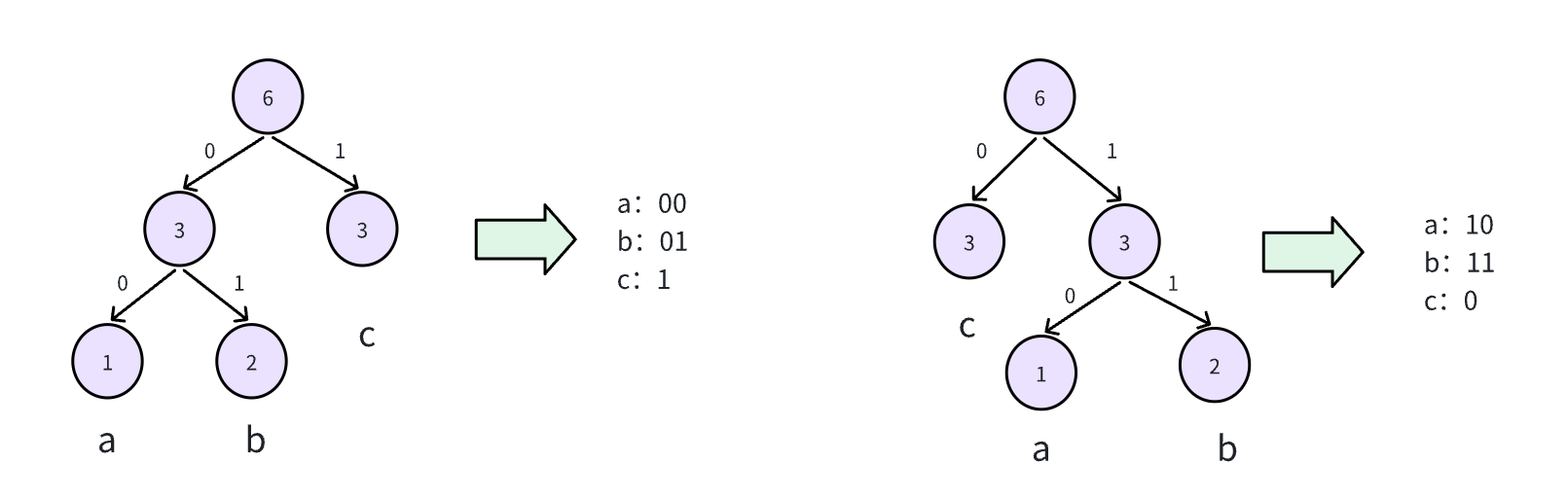
简单来说他是一种压缩算法，核心思想就是：​​用更短的二进制编码表示高频字符，用较长的编码表示低频字符；

用二进制表示字符：

假设有这么一个字符串：a b b c c c，现在需要使用二进制编码对其进行压缩；

可以这样表示每个字符：

a: 0  // 二进制0
b: 01 // 二进制 01
c: 10 // 二进制 10
    ...

但是这样的编码表示似乎并不是最优的，c的占比最多，而c所占编码bit位也最多，这显然并不是最优的；并且还会有解码的问题，比如： 010

此时怎么解码？ac还是ba？

针对这些问题，此时就可以依据哈夫曼编码的思想进行编码：

怎么进行哈夫曼编码？

核心步骤：​​

1. 频率统计​ ：统计待编码数据中每个字符的出现频率。
2. 构建哈夫曼树​ ：根据频次构建最优二叉树
3. 分配编码： 根据最优二叉树进行编码​

还是 a bb ccc 这个字符串，a：1次，b：2次，c：3次；

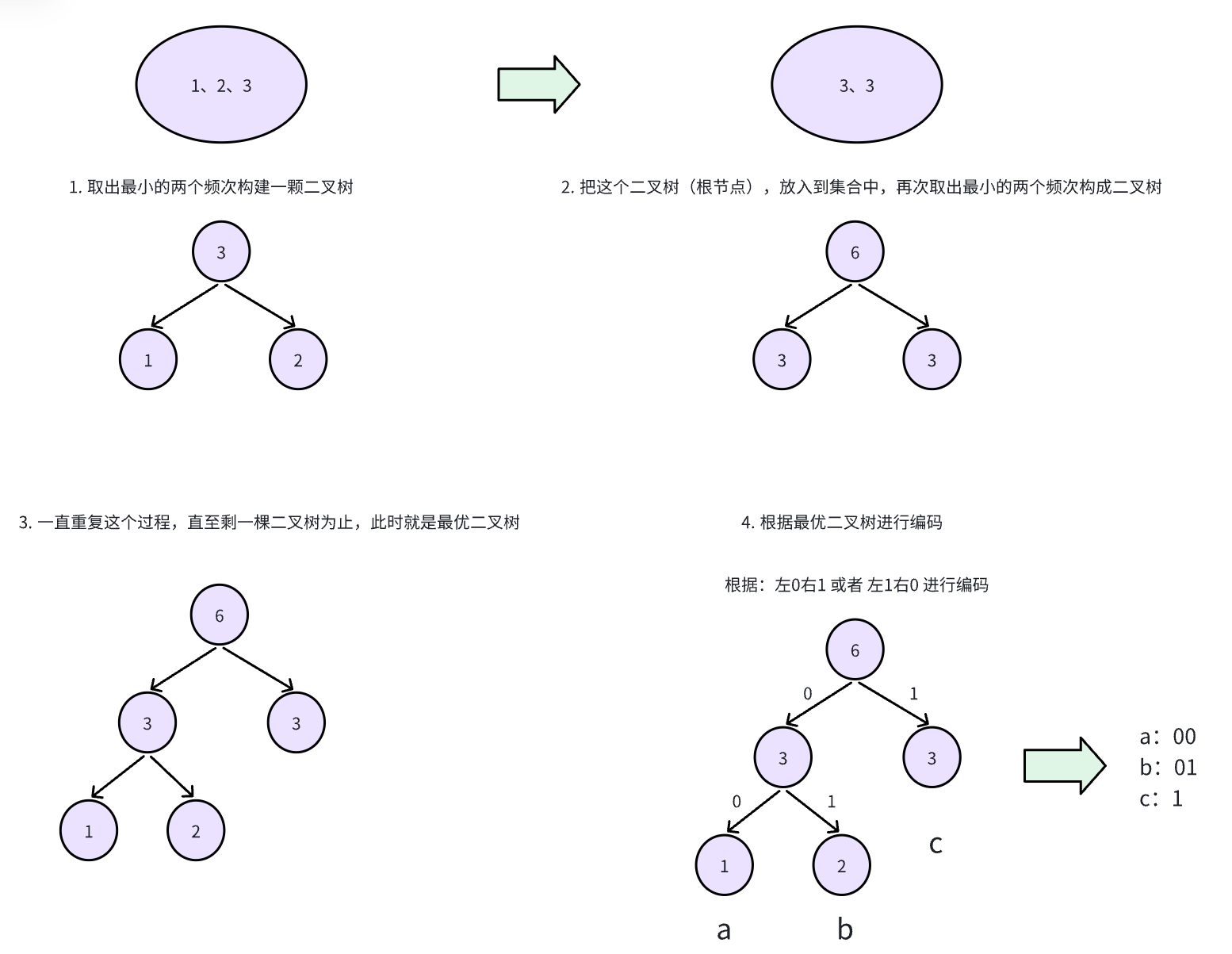
1. 把所有字符的频次放到一个集合中，每次取出最小的两个频次构建一颗二叉树；
2. 把这个二叉树（根节点），放入到集合中，再次取出最小的两个频次构成二叉树
3. 一直重复这个过程，直至剩一棵二叉树为止，此时就是最优二叉树
4. 根据最优二叉树进行编码（根据路径、以及字符频次进行编码）

算法考察

针对哈夫曼编码，主要考察两个问题：

1. 哈夫曼编码后的长度
2. 最终每个字符的编码集

问题一：求编码后的长度

哈夫曼编码_牛客题霸_牛客网

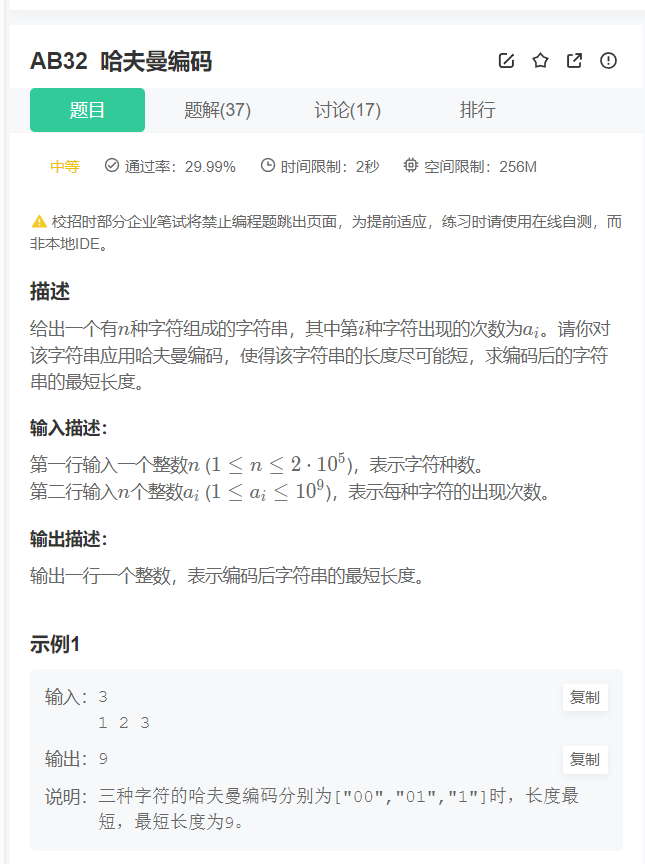
题目中给出了字符种类，以及各字符的频次；根据哈夫曼编码构建二叉树；

每次取出最小频次的两个值，可以借助堆（优先级队列）数据结构；

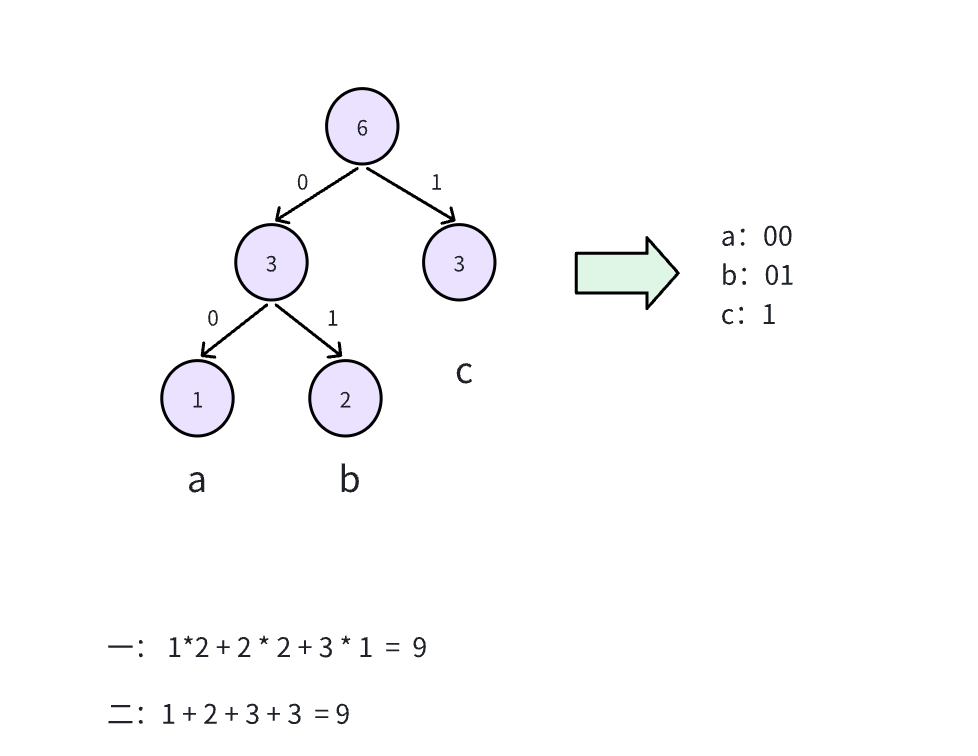
计算编码后的长度方式右两种：

1. 权重值 * 叶子节点到根节点的步数
2. 每次取出两个频次最小的节点构建新树时进行累加；

代码实现：

选用第二种方式进行计算（边构建边计算）

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
typedef long long LL;

int main() {
    LL ret= 0, n = 0;
    cin >> n;
    priority_queue<LL, vector<LL>, greater<LL>> heap;
    for(int i = 0; i < n; i++){
        LL x;
        cin >> x;
        heap.push(x);
    }

    while (heap.size() > 1) {
        LL t1 = heap.top(); heap.pop();
        LL t2 = heap.top(); heap.pop();
        heap.push(t1 + t2);
        ret += t1 + t2;
    }
    cout << ret;
}

问题二：求各字符编码集合

暂时没有找到相似的题目，但是可以依据哈夫曼编码_牛客题霸_牛客网 这道题来改编一下测试输出；

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
typedef long long LL;

// 声明二叉树的node节点
struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode() : val(0), left(nullptr), right(nullptr) {}
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left),
        right(right) {}
};

// 记录编码集合（根节点到叶子节点的所有路径）
vector<string> ret;
void dfs(TreeNode* root, string path) {

    if (!root->left && !root->right) {
        ret.push_back(path);
        return;
    }

    if (root->left) dfs(root->left, path + '0');
    if (root->right) dfs(root->right, path + '1');
}
vector<string> binaryTreePaths(TreeNode* root) {
    string path = "";
    if (root == nullptr) return ret;
    dfs(root, path);
    return ret;
}



int main() {
    LL n = 0;
    cin >> n;
    priority_queue<TreeNode*, vector<TreeNode*>, greater<TreeNode*>> heap;
    for (int i = 0; i < n; i++) {
        LL x;
        cin >> x;
        TreeNode* node = new TreeNode();
        heap.push(node);
    }
    // 构建最优二叉树
    while (heap.size() > 1) {
        auto t1 = heap.top();
        heap.pop();
        auto t2 = heap.top();
        heap.pop();
        TreeNode* node = new TreeNode(t1->val + t2->val, t2, t1);
        heap.push(node);

    }
    auto root = heap.top();
    // 输出结果
    for(auto s: binaryTreePaths(root)){
        cout << s << endl;
    }

}

测试输出：

题目示例：

输入: 
3
1 2 3

输出：9

说明：
三种字符的哈夫曼编码分别为["00","01","1"]时，长度最短，最短长度为9。

注意哈夫曼编码并不是唯一的，在构建最优二叉树时，左右子树节点不同，编码结果也会不同；