目录
[check_sys() 函数详解](#check_sys() 函数详解)
[1. 变量声明和初始化](#1. 变量声明和初始化)
[2. 初始化时的赋值](#2. 初始化时的赋值)
[3. printf 输出](#3. printf 输出)
[4. 具体每个变量的提升和输出](#4. 具体每个变量的提升和输出)
[5. 最终输出](#5. 最终输出)
[注意:char 的符号性](#注意:char 的符号性)
[1. 变量 a 的声明和初始化](#1. 变量 a 的声明和初始化)
[2. printf 格式化输出](#2. printf 格式化输出)
[3. 不匹配的格式说明符](#3. 不匹配的格式说明符)
[4. 实际输出(在常见的二进制补码系统中)](#4. 实际输出(在常见的二进制补码系统中))
[5. 另一种理解(直接从char到unsigned int的转换)(了解即可)](#5. 另一种理解(直接从char到unsigned int的转换)(了解即可))
[6. 总结输出](#6. 总结输出)
[7. 最终答案](#7. 最终答案)
[1. 变量 a 的声明和初始化](#1. 变量 a 的声明和初始化)
[2. 有符号char的溢出行为](#2. 有符号char的溢出行为)
[3. printf 格式化输出](#3. printf 格式化输出)
[4. 类型不匹配的后果](#4. 类型不匹配的后果)
[5. 实际输出计算(在32位系统,二进制补码)](#5. 实际输出计算(在32位系统,二进制补码))
[6. 另一种理解方式](#6. 另一种理解方式)
[7. 如果char是无符号的?](#7. 如果char是无符号的?)
[8. 最终输出](#8. 最终输出)
[1. ptr1[-1] 的值](#1. ptr1[-1] 的值)
[2. *ptr2 的值(小端序假设)](#2. *ptr2 的值(小端序假设))
一、回顾与引入:整数在内存中的存储方式
在介绍strlen操作符时,我们已经提到过以下内容:
整数的二进制表示方法有三种,分别是原码、反码和补码。
对于有符号整数,三种表示方法都包含符号位和数值位两个部分。符号位以"0"表示正数,"1"表示负数,通常位于最高位,其余部分为数值位。
-
正整数的原码、反码和补码完全相同。
-
负整数的原码、反码和补码则各不相同。
具体转换方式如下:
-
原码:直接根据数值的正负形式翻译成二进制表示。
-
反码:在原码的基础上,保持符号位不变,其余各位按位取反。
-
补码:在反码的基础上加 1 得到。
对于整型数据,其在内存中实际存储的是二进制补码形式。
为什么要采用补码存储?
在计算机系统中,数值一律采用补码来表示和存储,主要原因包括:
-
使用补码可以统一处理符号位与数值部分,简化硬件设计;
-
补码能够将加法和减法运算统一为加法操作(CPU 通常只内置加法器);
-
补码与原码之间的转换过程一致,无需额外的硬件电路支持,提高了计算效率并降低了系统复杂度。
二、大小端字节序及其判断方法
在我们了解整数在内存中的存储方式后,通过以下代码调试可以观察到一个现象:
cpp
#include <stdio.h>
int main()
{
int a = 0x11223344;
return 0;
}调试时会发现,变量 a 中的值 0x11223344 在内存中是以字节为单位倒序存储的。为什么会这样呢?
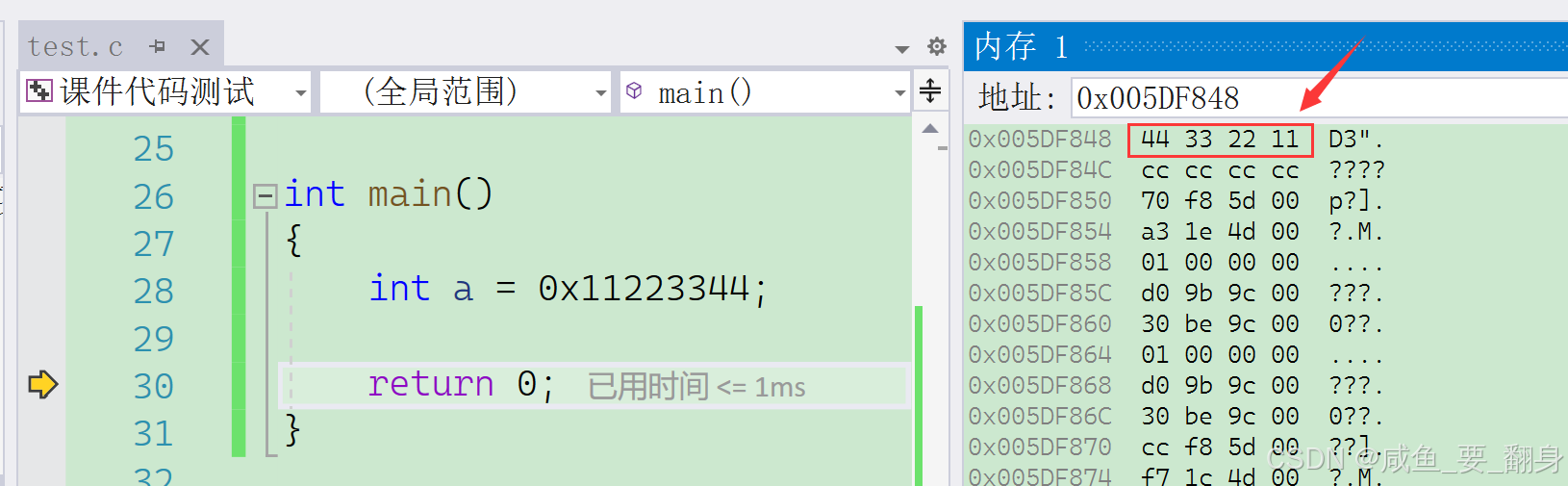
1、什么是大小端?
**当一个数据超过一个字节时,在内存中的存储顺序就涉及字节序的问题。根据不同的存储顺序,可分为大端字节序(Big-Endian)和小端字节序(Little-Endian)。**其具体定义为:
-
大端模式:数据的低位字节(即权值较小的字节)保存在内存的高地址处,而数据的高位字节保存在内存的低地址处。
-
小端模式:数据的低位字节保存在内存的低地址处,而数据的高位字节保存在内存的高地址处。
理解并记住这两种模式有助于我们在不同平台或网络传输中正确处理多字节数据。
2、为什么存在大小端?
计算机系统中以字节为单位编址,每个地址对应一个字节(8 bit)。但在C语言中,除了 char(8 bit)外,还有 short(16 bit)、int 和 long(32 bit 或更长,取决于编译器和架构)等类型。对于寄存器宽度大于8位的处理器(如16位或32位CPU),如何排列多个字节就成为一个必须解决的问题,因此出现了大端和小端两种存储模式。
举例来说,一个16位的变量 short x,其地址为 0x0010,值为 0x1122。其中 0x11 是高字节,0x22 是低字节。在大端模式下,0x11 存放在 0x0010(低地址),0x22 存放在 0x0011(高地址);小端模式则相反。常见的x86架构为小端模式,而KEIL C51通常为大端模式。许多ARM和DSP处理器默认为小端模式,部分ARM处理器还支持通过硬件配置选择字节序。
3、练习
练习1:简述大小端概念并设计判断程序(百度面试题)
要求:简述大端和小端字节序的概念,并编写程序判断当前机器的字节序。
参考代码1:
cpp
#include <stdio.h>
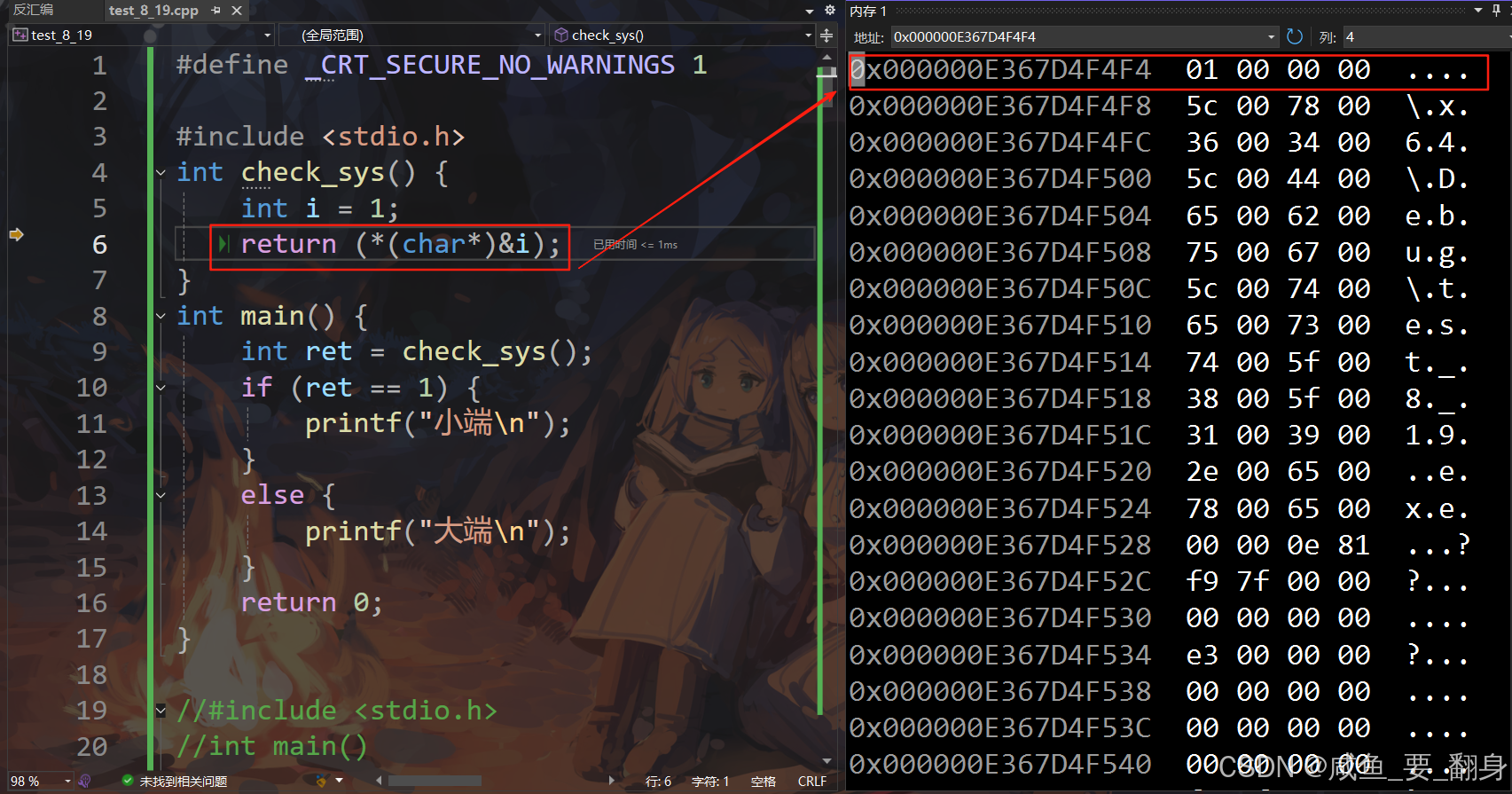
int check_sys() {
int i = 1;
return (*(char *)&i);
}
int main() {
int ret = check_sys();
if(ret == 1) {
printf("小端\n");
} else {
printf("大端\n");
}
return 0;
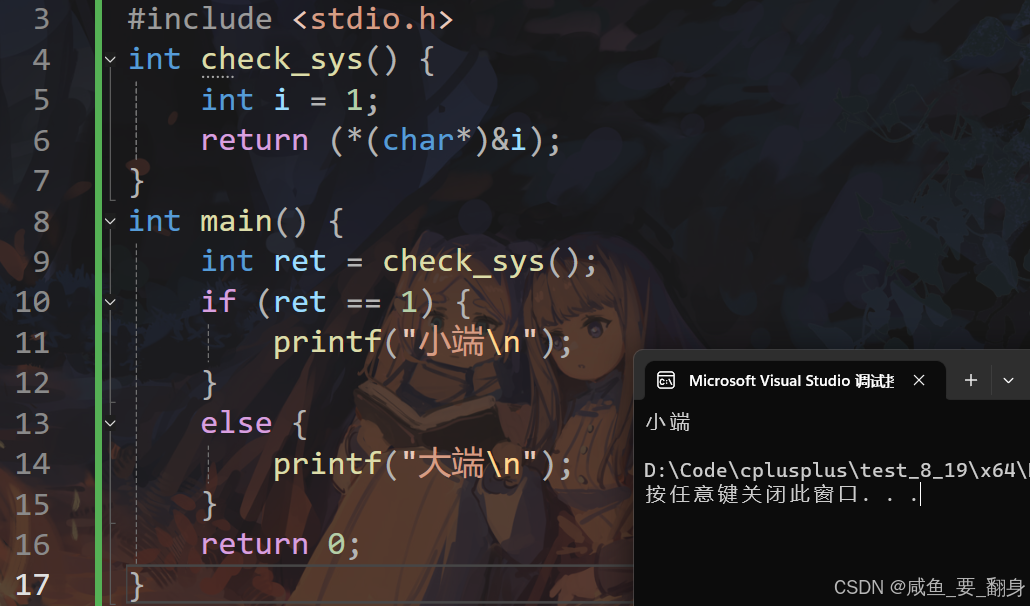
}关键原理:字节序(Endianness)
小端模式(Little-endian)
-
低位字节存储在低地址
-
对于整数
1(0x00000001):- 内存布局(地址从低到高):
01 00 00 00
- 内存布局(地址从低到高):
大端模式(Big-endian)
-
高位字节存储在低地址
-
对于整数
1(0x00000001):- 内存布局(地址从低到高):
00 00 00 01
- 内存布局(地址从低到高):
check_sys() 函数详解
-
int i = 1;在内存中分配4字节空间存储整数1 -
&i获取变量i的起始地址(最低字节的地址) -
(char *)&i-
将int指针强制转换为char指针
-
char指针指向内存的第一个字节
-
-
*(char *)&i解引用char指针,获取第一个字节的值
结果分析
-
小端系统 :第一个字节是
0x01,返回1 -
大端系统 :第一个字节是
0x00,返回0
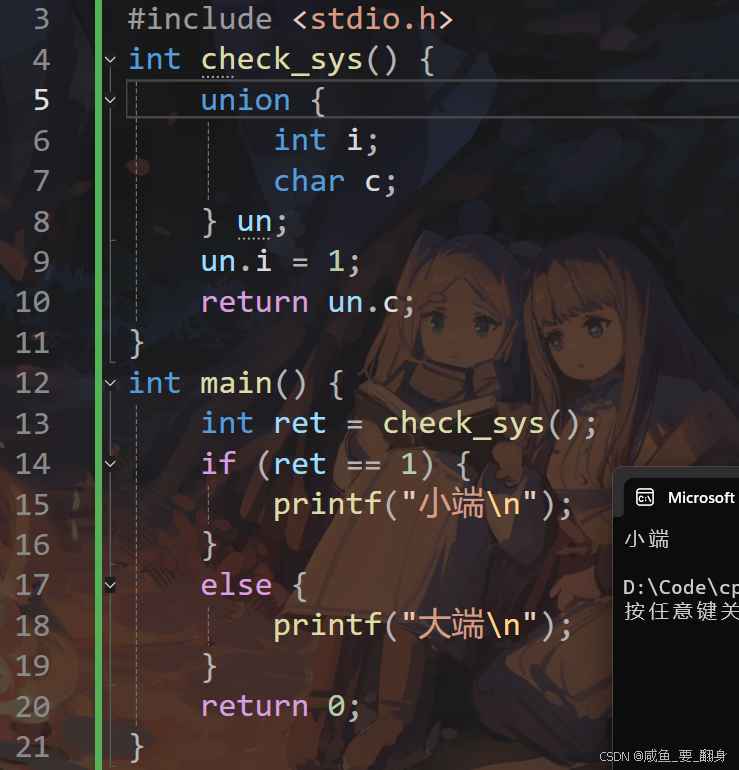
参考代码2(使用联合体):
cpp
int check_sys() {
union {
int i;
char c;
} un;
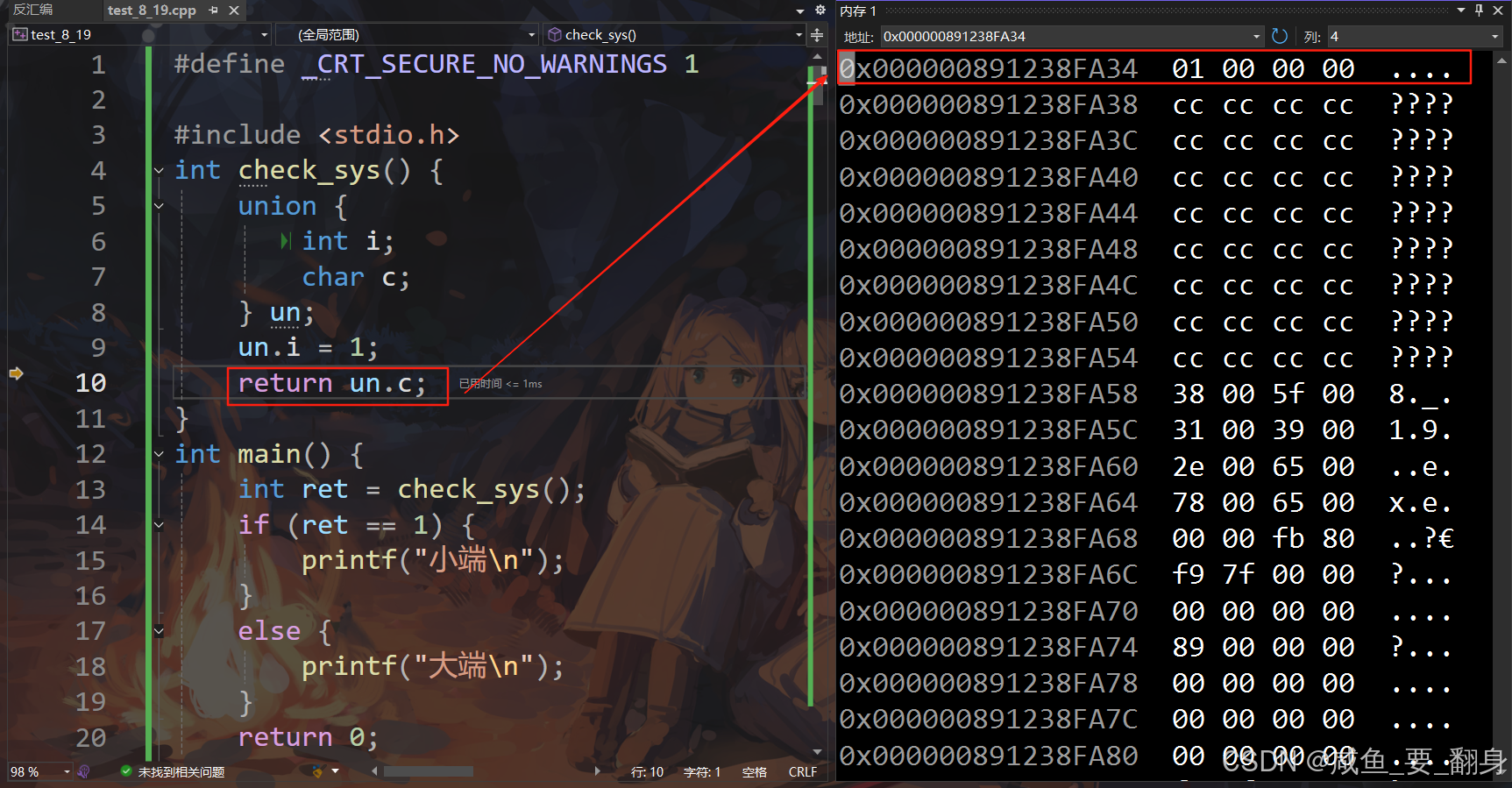
un.i = 1;
return un.c;
}联合体(union)的特性
-
联合体的所有成员共享同一块内存空间
-
大小由最大的成员决定(这里int通常是4字节,char是1字节)
-
对任何一个成员的修改都会影响其他成员的值
内存布局分析
当 un.i = 1 时:
-
整数
1的十六进制表示为:0x00000001 -
在联合体的共享内存中存储这个值
小端模式
cpp
内存地址(低→高): 0x00 0x01 0x02 0x03
存储数据: 0x01 0x00 0x00 0x00
↑ 最低地址存储最低有效字节大端模式
cpp
内存地址(低→高): 0x00 0x01 0x02 0x03
存储数据: 0x00 0x00 0x00 0x01
↑ 最低地址存储最高有效字节工作原理
-
un.i = 1:将整数1存入联合体的4字节空间 -
un.c:访问联合体的第一个字节(最低地址)-
小端 :第一个字节是
0x01→ 返回1 -
大端 :第一个字节是
0x00→ 返回0
-
练习2:有符号与无符号字符型的输出
cpp
#include <stdio.h>
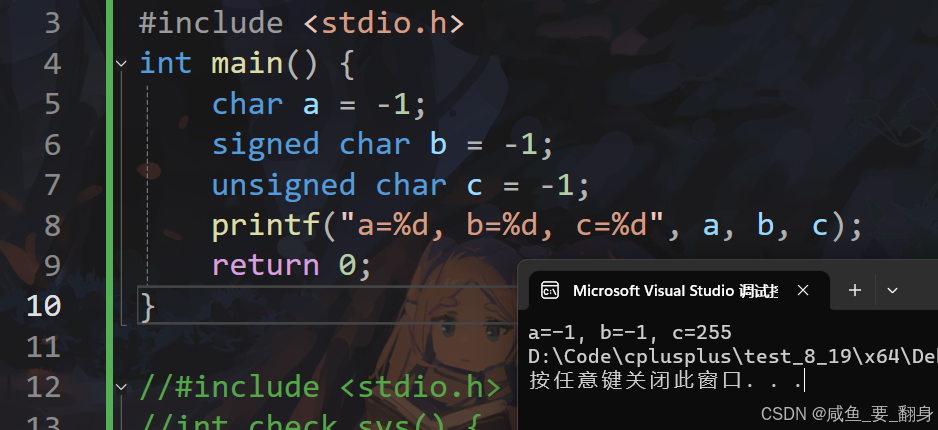
int main() {
char a = -1;
signed char b = -1;
unsigned char c = -1;
printf("a=%d, b=%d, c=%d", a, b, c);
return 0;
}1. 变量声明和初始化
-
char a = -1;在大多数系统中,char默认是有符号的(相当于signed char),但这一点取决于编译器和平台。通常,char可以是有符号或无符号的,但常见的是有符号的。这里我们假设char是有符号的(如大多数x86系统)。 -
signed char b = -1;明确声明为有符号字符,初始化为 -1。 -
unsigned char c = -1;无符号字符类型,初始化为 -1。
2. 初始化时的赋值
-
对于有符号类型(
a和b),-1 可以直接表示(二进制补码形式)。 -
对于无符号类型(
c),初始化赋值为 -1。由于无符号类型不能表示负数,所以会发生转换:-1 会被转换为无符号类型所允许的最大值(因为无符号类型是模运算)。具体来说,对于
unsigned char(通常是8位),范围是 0 到 255。-1 的二进制补码表示是
11111111(所有位为1),当解释为无符号时,就是 255。
3. printf 输出
-
printf使用%d格式化输出,它期望的是int类型参数。所以
a,b,c都会先被提升为int类型(整数提升),然后传递给printf。 -
整数提升规则:
-
对于有符号类型(如
signed char),提升时进行符号扩展(即高位填充符号位)。 -
对于无符号类型(如
unsigned char),提升时高位填充0。
-
4. 具体每个变量的提升和输出
-
a(假设是有符号 char):-
初始值:-1(二进制
11111111) -
提升为
int:符号扩展,高位全填1(即11111111 11111111 11111111 11111111),这仍然是 -1。 -
输出:
a=-1
-
-
b(signed char):-
与
a相同:-1(二进制11111111) -
提升为
int:符号扩展,得到 -1。 -
输出:
b=-1
-
-
c(unsigned char):-
初始值:-1 被转换为无符号值 255(二进制
11111111)。 -
提升为
int:因为是无符号,高位填充0(即00000000 00000000 00000000 11111111),所以是 255。 -
输出:
c=255
-
5. 最终输出
因此,输出为:a=-1, b=-1, c=255
注意:char 的符号性
如果系统默认将 char 定义为无符号(如某些ARM编译器),那么 a 的行为会与 c 相同(输出255)。但常见情况下(如GCC在x86上),char 是有符号的,所以输出为 -1。
练习3:字符型变量以无符号格式输出
cpp
#include <stdio.h>
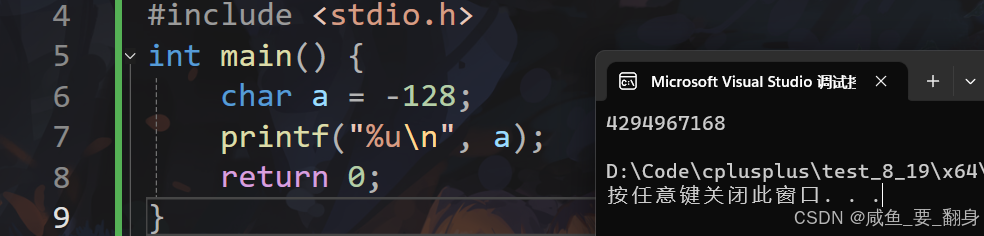
int main() {
char a = -128;
printf("%u\n", a);
return 0;
}1. 变量 a 的声明和初始化
-
char a = -128;:这里声明了一个char类型的变量a,并初始化为-128。 -
在大多数系统中,
char默认是有符号 的(signed char),其范围通常是-128到127(假设是8位二进制补码表示)。 -
-128正好是char类型能表示的最小值(二进制表示为10000000)。
2. printf 格式化输出
-
printf("%u\n", a);:这里使用%u格式说明符来输出a的值。%u用于输出无符号十进制整数。 -
但注意:
a是char类型(本质上是一个整数类型),当传递给printf时,由于可变参数函数的默认参数提升规则(default argument promotion),a会被提升为int类型(因为char是比int更小的整数类型)。-
具体来说:
char(无论是signed char还是unsigned char)在传递给可变参数函数(如printf)时,会被提升为int(如果int可以表示所有char的值)或unsigned int(但通常int可以表示)。 -
对于有符号的
char a = -128,提升为int后仍然是-128(因为int可以表示-128)。
-
3. 不匹配的格式说明符
-
%u期望一个unsigned int类型的参数,但实际传递的是int类型的-128(由于提升)。 -
这会导致未定义行为(undefined behavior),因为C标准规定:如果格式说明符和实际参数类型不匹配,行为是未定义的。
-
然而,在大多数实现中,会直接按位解释(即:将传递的
int类型的二进制表示直接当作unsigned int来解读)。
4. 实际输出(在常见的二进制补码系统中)
-
a的原始值(char类型)是-128,其二进制表示(8位)是:10000000。 -
当提升为
int时(假设32位int),由于符号扩展,-128的int表示是:二进制:11111111 11111111 11111111 10000000(即全1填充到最高位,直到第8位为1,其余低位为0)。 -
当用
%u解释这个int值时(即把相同的二进制位模式当作无符号整数),得到的无符号整数值是:-
11111111 11111111 11111111 10000000(二进制) =4294967168(十进制)。 -
计算:最高位是1,所以这是一个很大的正数(2^32 - 128 = 4294967168)。
-
5. 另一种理解(直接从char到unsigned int的转换)(了解即可)
-
实际上,在传递过程中,
char先被提升为int(值为-128),然后被printf用%u解读(即强制转换为unsigned int)。 -
有符号整数到无符号整数的转换规则:C标准规定,如果源值是负数,则转换结果为"该值加上无符号类型最大值加1"(即模运算)。
-
所以,
(unsigned int)(-128)=-128 + UINT_MAX + 1=UINT_MAX - 127。 -
在32位系统中,
UINT_MAX是4294967295,所以结果是4294967295 - 127 = 4294967168。
-
6. 总结输出
-
因此,在常见的系统(32位,二进制补码)上,输出将是
4294967168。 -
注意:如果
char是无符号的(某些系统可能定义char为unsigned char),那么a = -128实际上会赋值128(因为无符号char的范围是0-255),但这里我们假设char是有符号的(这是大多数系统的默认行为)。
7. 最终答案
所以,这段代码的输出是:
cpp
#include <stdio.h>
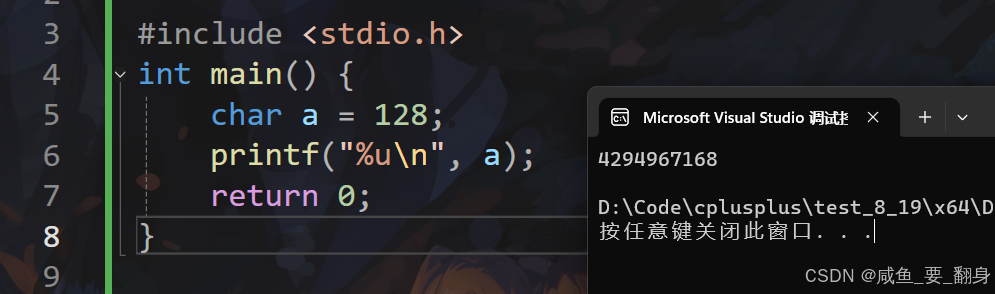
int main() {
char a = 128;
printf("%u\n", a);
return 0;
}1. 变量 a 的声明和初始化
-
char a = 128;:声明了一个char类型的变量a,并初始化为128。 -
在大多数系统中,
char默认是有符号 的(signed char),其范围是-128到127(8位二进制补码表示)。 -
128超出了signed char的正数范围(127是最大值),所以这里会发生整数溢出。
2. 有符号char的溢出行为
-
在C语言中,有符号整数溢出是未定义行为(undefined behavior)。
-
但在大多数实现(使用二进制补码)中,数值会"环绕"(wrap around):
-
127(01111111) + 1 =-128(10000000) -
所以
128会被解释为-128(因为128 = 127 + 1)
-
3. printf 格式化输出
-
printf("%u\n", a);:使用%u格式说明符输出a的值。 -
由于可变参数函数的默认参数提升规则,
char类型的a会被提升为int类型。 -
%u期望一个unsigned int类型的参数,但实际传递的是提升后的int类型值(-128)。
4. 类型不匹配的后果
-
这是未定义行为 ,因为格式说明符
%u与实际参数类型(int)不匹配。 -
但在大多数系统中,会直接按位解释(将
int的二进制表示当作unsigned int来解读)。
5. 实际输出计算(在32位系统,二进制补码)
-
a的实际值:由于溢出,a = 128被存储为-128(二进制:10000000) -
提升为
int:-128的32位二进制补码表示是:11111111 11111111 11111111 10000000 -
当用
%u解释这个位模式时,被当作无符号整数:-
二进制:
11111111 11111111 11111111 10000000 -
十进制值:2³² - 128 = 4294967296 - 128 = 4294967168
-
6. 另一种理解方式
-
从有符号到无符号的转换规则:
(unsigned int)(-128) = -128 + UINT_MAX + 1 -
在32位系统中,
UINT_MAX = 4294967295 -
所以:
4294967295 + 1 - 128 = 4294967168
7. 如果char是无符号的?
-
如果系统默认
char是unsigned char(范围0-255),那么:-
a = 128是有效的 -
提升为
int时是128(正数) -
用
%u输出:128
-
-
但大多数系统(如x86)默认
char是有符号的。
8. 最终输出
在常见的系统(32位,二进制补码,char有符号)上,输出为:
练习4:字符数组与strlen
cpp
#include <stdio.h>
#include <string.h>
int main() {
char a[1000];
int i;
for(i = 0; i < 1000; i++) {
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}-
数组
a的初始化:-
a是一个长度为1000的字符数组(char类型,在大多数系统中是有符号的,范围是-128到127)。 -
循环中,
a[i] = -1 - i对每个元素赋值。-
当
i=0:a[0] = -1 - 0 = -1 -
当
i=1:a[1] = -1 - 1 = -2 -
...
-
当
i=127:a[127] = -1 - 127 = -128(这是char能表示的最小值) -
当
i=128:a[128] = -1 - 128 = -129,但char只能表示-128到127,所以会发生溢出。-
在补码表示中,-129的二进制是(假设8位char):-129的补码是(超出8位范围),实际会截断为8位。
-
计算:-129的二进制(16位表示)是
1111111101111111,截取低8位是01111111(即127)。 -
类似地,-130截断为126,依此类推。
-
-
实际上,我们可以用取模的方式来计算溢出后的值(因为C标准规定有符号整数溢出是未定义行为,但通常实现是环绕的):
-
对于有符号char,值会以256为模环绕(因为8位有符号数的表示范围是-128~127,共256个值)。
-
所以,
-1 - i的实际值可以通过(-1 - i) % 256来得到(但需要调整到在-128~127之间)。
更直接的方式是考虑序列:
-
i=0: -1
-
i=1: -2
-
...
-
i=127: -128
-
i=128: -129 -> 由于溢出,实际为127(因为-129 + 256 = 127)
-
i=129: -130 -> 126
-
...
-
i=255: -256 -> 0
-
i=256: -257 -> -1(因为-257 + 256*2 = 255?不对,实际上应该模256,但注意有符号数的表示)
实际上,我们可以写出前几个值:
i: 0 1 2 ... 127 128 129 130 ... 255 256 ...
a[i]: -1, -2, -3 ... -128,127,126,125 ... 0, -1, ...
注意,当i=255时:-1-255 = -256,模256后是0(因为-256正好是256的倍数,所以余0)。
当i=256时:-1-256=-257,模256:-257 % 256 = -1(因为-257 = -256*1 -1,所以余-1?但实际在8位中,它表示成-1)。
但这里我们不需要所有值,我们只需要知道第一个0出现在哪里?因为
strlen计算的是从开始到第一个'\0'(即0)的字符数。 -
-
strlen的工作 :strlen(a)从a[0]开始扫描,直到遇到第一个值为0的字节(即'\0'),然后返回之前的字符个数(不包括0本身)。 -
寻找第一个0:
-
我们需要找到最小的
i,使得a[i] == 0。 -
根据上面的赋值:
a[i] = -1 - i。 -
设
a[i] == 0,即-1 - i == 0?但这样i=-1,显然不对(因为i从0开始)。 -
实际上,由于溢出,我们需要解方程:
(-1 - i) mod 256 = 0(即-1-i是256的倍数)。 -
即
-1 - i = 256 * k(k为整数),因为值在0时停止。 -
取k=-1(因为i非负,所以k应为负):
-1 - i = -256=>i = 255。所以当i=255时,
a[255] = -1-255 = -256,模256后为0(因为-256是256的整数倍,所以余0)。
因此,第一个0出现在索引255处。
-
-
验证:
-
i=255时:
a[255] = -1-255 = -256。在8位有符号表示中,-256的二进制(补码)本需要9位(100000000),截断低8位后是00000000(即0)。 -
所以
a[255] = 0。
-
-
strlen(a)的返回值 :strlen从a[0]开始计数,直到a[254](因为a[255]是0,不计入),所以总共255个字符。
因此,程序输出的是255。
练习5:无符号变量的循环
cpp
#include <stdio.h>
unsigned char i = 0;
int main() {
for(i = 0; i <= 255; i++) {
printf("hello world\n");
}
return 0;
}问题原因
-
unsigned char i的范围是 0 到 255(8位无符号字符) -
当
i增加到 255 后,执行i++会导致整数溢出 -
在无符号整型中,溢出会回绕:255 + 1 = 0
-
因此条件
i <= 255永远为真,循环永远不会结束
cpp
#include <stdio.h>
int main() {
unsigned int i;
for(i = 9; i >= 0; i--) {
printf("%u\n", i);
}
return 0;
}问题原因
-
unsigned int i是无符号整型,范围是0到UINT_MAX(通常是 0 到 4,294,967,295) -
当
i = 0时,执行i--会导致下溢 -
在无符号整型中,下溢会回绕:0 - 1 = UINT_MAX(非常大的正数)
-
因此条件
i >= 0永远为真(因为无符号数永远 ≥ 0),循环永远不会结束
练习6:指针运算与字节序(x86小端模式)
cpp
#include <stdio.h>
int main() {
int a[4] = {1, 2, 3, 4};
int *ptr1 = (int *)(&a + 1);
int *ptr2 = (int *)((int)a + 1);
printf("%x, %x", ptr1[-1], *ptr2);
return 0;
}这段代码涉及指针运算和类型转换,行为是未定义的(UB),但在小端序机器上可能有特定输出。我们来分析:
代码分析
cpp
int a[4] = {1, 2, 3, 4};
int *ptr1 = (int *)(&a + 1); // 指向数组末尾之后
int *ptr2 = (int *)((int)a + 1); // 将地址转为整数加1再转回指针
printf("%x, %x", ptr1[-1], *ptr2); // 输出1. ptr1[-1] 的值
-
&a是「指向整个数组的指针」,类型是int (*)[4] -
&a + 1会跳过整个数组(16字节),指向数组末尾之后 -
(int *)强制转换为int*,现在ptr1指向a[4](不存在) -
ptr1[-1]等价于*(ptr1 - 1),即从末尾回退一个int,指向a[3] -
所以
ptr1[-1]是4
2. *ptr2 的值(小端序假设)
-
a是数组首地址(假设为0x1000) -
(int)a将地址转为整数(假设0x1000) -
(int)a + 1得到0x1001 -
(int *)再转回指针,现在ptr2指向0x1001(非对齐访问,UB!)
在小端机器上,数组 a 在内存中的布局(每个int占4字节):
cpp
地址 数据(字节序,小端)
0x1000: 01 00 00 00 // a[0] = 1
0x1004: 02 00 00 00 // a[1] = 2
0x1008: 03 00 00 00 // a[2] = 3
0x100C: 04 00 00 00 // a[3] = 4ptr2 指向 0x1001,会读取从 0x1001 开始的4字节:
-
取
0x1001、0x1002、0x1003、0x1004这4个字节 -
字节数据:
00 00 00 02(小端序) -
解释为int:
0x02000000(十进制 33554432)
输出
所以输出可能是:4, 2000000(%x输出十六进制)
注意
-
未定义行为 :
(int)a + 1破坏了对齐要求,可能崩溃或得到意外值 -
依赖字节序:仅在小端机器得到上述结果,大端会不同
-
依赖编译器/平台:实际结果因实现而异
总结
在小端序x86系统上,输出可能是:
但这段代码不应该在实际中使用,因为它包含了多个未定义行为和对齐问题。