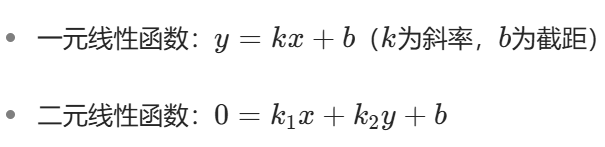深度学习入门详解：从神经网络到实践应用

一、引言：深度学习的崛起与意义

二、深度学习的基础概念：从机器学习到神经网络

[2.1 深度学习与机器学习的关系](#2.1 深度学习与机器学习的关系)

[2.2 神经网络：深度学习的核心载体](#2.2 神经网络：深度学习的核心载体)

三、神经网络的基本构成：神经元与激活函数

[3.1 神经元的数学表达](#3.1 神经元的数学表达)

[3.1.1 从线性函数到神经元模型](#3.1.1 从线性函数到神经元模型)

[3.1.2 偏置的特殊处理](#3.1.2 偏置的特殊处理)

[3.2 激活函数：引入非线性的关键](#3.2 激活函数：引入非线性的关键)

[3.2.1 常用激活函数：sigmoid函数](#3.2.1 常用激活函数：sigmoid函数)

[3.2.2 激活函数的作用](#3.2.2 激活函数的作用)

四、感知器：最简单的神经网络

[4.1 感知器的结构](#4.1 感知器的结构)

[4.1.1 感知器的数学表达](#4.1.1 感知器的数学表达)

[4.1.2 感知器的局限性](#4.1.2 感知器的局限性)

[4.2 感知器的训练过程](#4.2 感知器的训练过程)

五、多层感知器：突破线性限制的神经网络

[5.1 隐藏层的引入](#5.1 隐藏层的引入)

[5.1.1 隐藏层的作用](#5.1.1 隐藏层的作用)

[5.1.2 多层感知器的数学表达](#5.1.2 多层感知器的数学表达)

[5.2 偏置节点的作用](#5.2 偏置节点的作用)

[5.3 中间层节点数的设计](#5.3 中间层节点数的设计)

六、模型训练的核心：损失函数与正则化

[6.1 损失函数：衡量预测误差的指标](#6.1 损失函数：衡量预测误差的指标)

[6.1.1 0-1损失函数](#6.1.1 0-1损失函数)

[6.1.2 均方差损失（MSE）](#6.1.2 均方差损失（MSE）)

[6.1.3 交叉熵损失](#6.1.3 交叉熵损失)

[6.2 多分类任务的损失计算](#6.2 多分类任务的损失计算)

[6.3 正则化：防止过拟合的关键](#6.3 正则化：防止过拟合的关键)

[6.3.1 L1正则化](#6.3.1 L1正则化)

[6.3.2 L2正则化](#6.3.2 L2正则化)

[6.3.3 正则化的作用示例](#6.3.3 正则化的作用示例)

七、优化算法：梯度下降与反向传播

[7.1 梯度下降：寻找最优参数的方法](#7.1 梯度下降：寻找最优参数的方法)

[7.1.1 梯度的概念](#7.1.1 梯度的概念)

[7.1.2 梯度下降的步骤](#7.1.2 梯度下降的步骤)

[7.1.3 学习率的选择](#7.1.3 学习率的选择)

[7.2 BP神经网络：误差反向传播算法](#7.2 BP神经网络：误差反向传播算法)

[7.2.1 BP算法的步骤](#7.2.1 BP算法的步骤)

[7.2.2 链式法则的应用](#7.2.2 链式法则的应用)

八、深度神经网络：从理论到实践

[8.1 深度神经网络的特点](#8.1 深度神经网络的特点)

[8.2 典型案例：ChatGPT的背后](#8.2 典型案例：ChatGPT的背后)

[8.3 深度学习框架的选择](#8.3 深度学习框架的选择)

九、总结与学习路径

[9.1 核心知识点回顾](#9.1 核心知识点回顾)

[9.2 学习建议](#9.2 学习建议)

一、引言：深度学习的崛起与意义

在人工智能的浪潮中，深度学习无疑是最耀眼的明星。从AlphaGo击败世界围棋冠军，到ChatGPT实现自然语言的流畅交互，再到自动驾驶、医疗影像诊断等领域的突破，深度学习正以惊人的速度重塑着我们的世界。作为机器学习的一个重要分支，深度学习通过模拟人类大脑的神经网络结构，让计算机具备了从海量数据中自主学习规律的能力。

本文将以通俗易懂的方式，带大家从零开始走进深度学习的世界。我们将从最基础的神经网络概念讲起，逐步深入到感知器、多层感知器、模型训练方法等核心内容，最终结合实际案例理解深度学习的应用原理。无论你是计算机专业的学生、刚入行的程序员，还是对AI感兴趣的爱好者，掌握这些基础知识都将为你打开深度学习的大门。

二、深度学习的基础概念：从机器学习到神经网络

2.1 深度学习与机器学习的关系

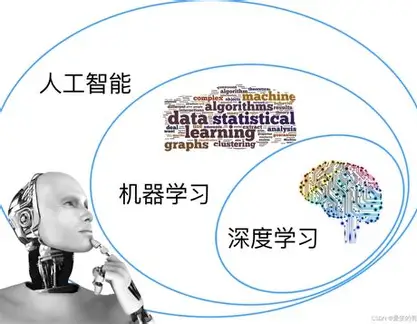
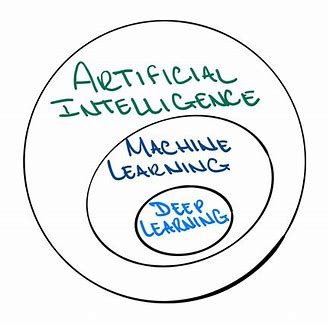
深度学习（Deep Learning，DL）是机器学习（Machine Learning，ML）领域的一个重要研究方向。如果将人工智能比作一座大厦，那么机器学习就是大厦的基石，而深度学习则是大厦中最璀璨的高层建筑。

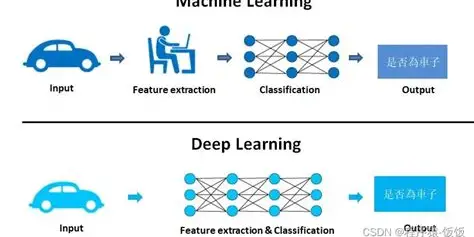
机器学习：通过算法让计算机从数据中学习规律，完成分类、回归等任务。传统机器学习需要人工设计特征，例如在图像识别中手动提取边缘、纹理等特征。
深度学习：无需人工设计特征，而是通过多层神经网络自动学习数据的特征表示。例如，在图像识别中，浅层网络学习边缘特征，中层网络学习部件特征，深层网络学习整体特征。

简单来说，深度学习是"端到端"的学习，它将特征提取和模型训练融为一体，极大地提升了复杂任务的处理能力。

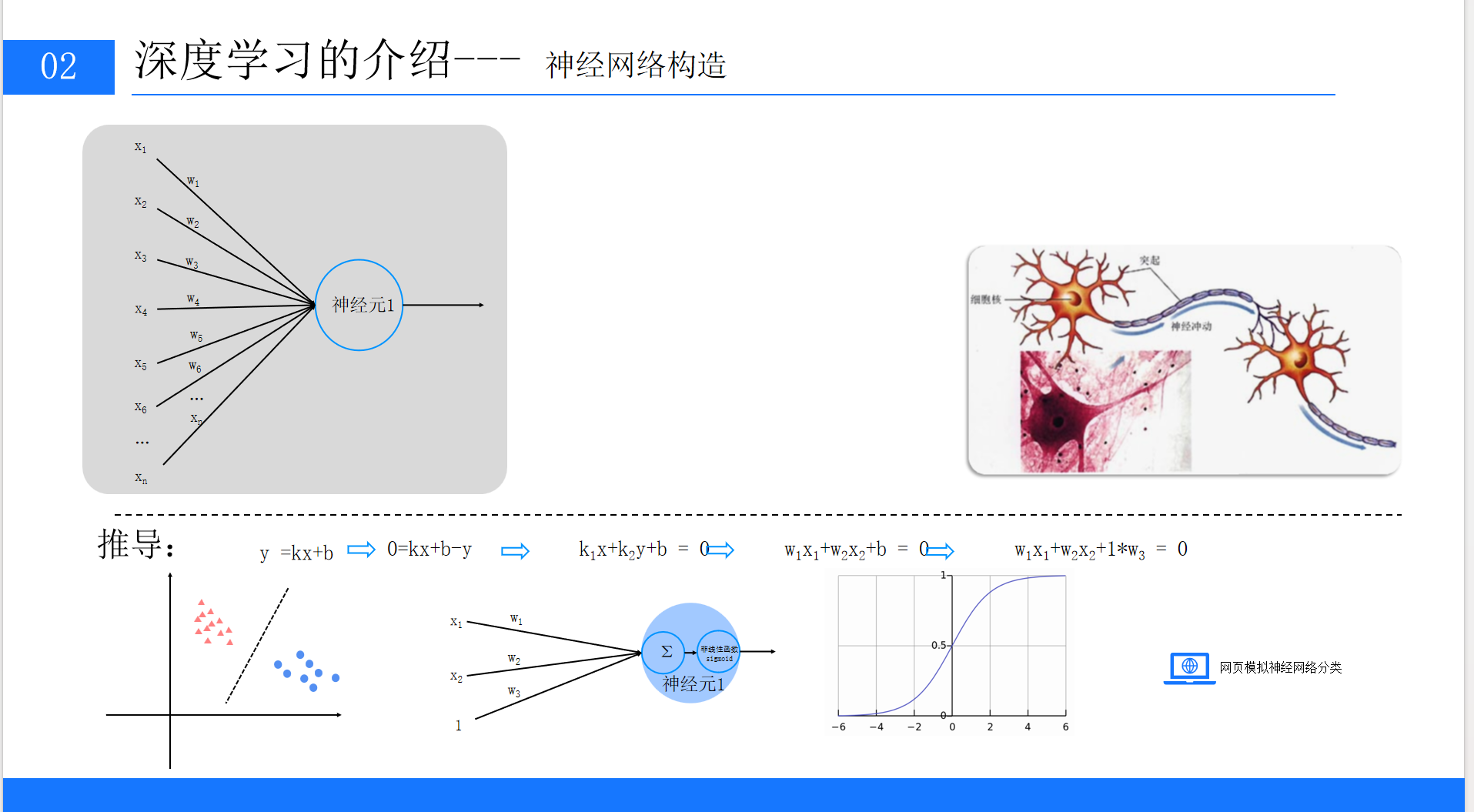
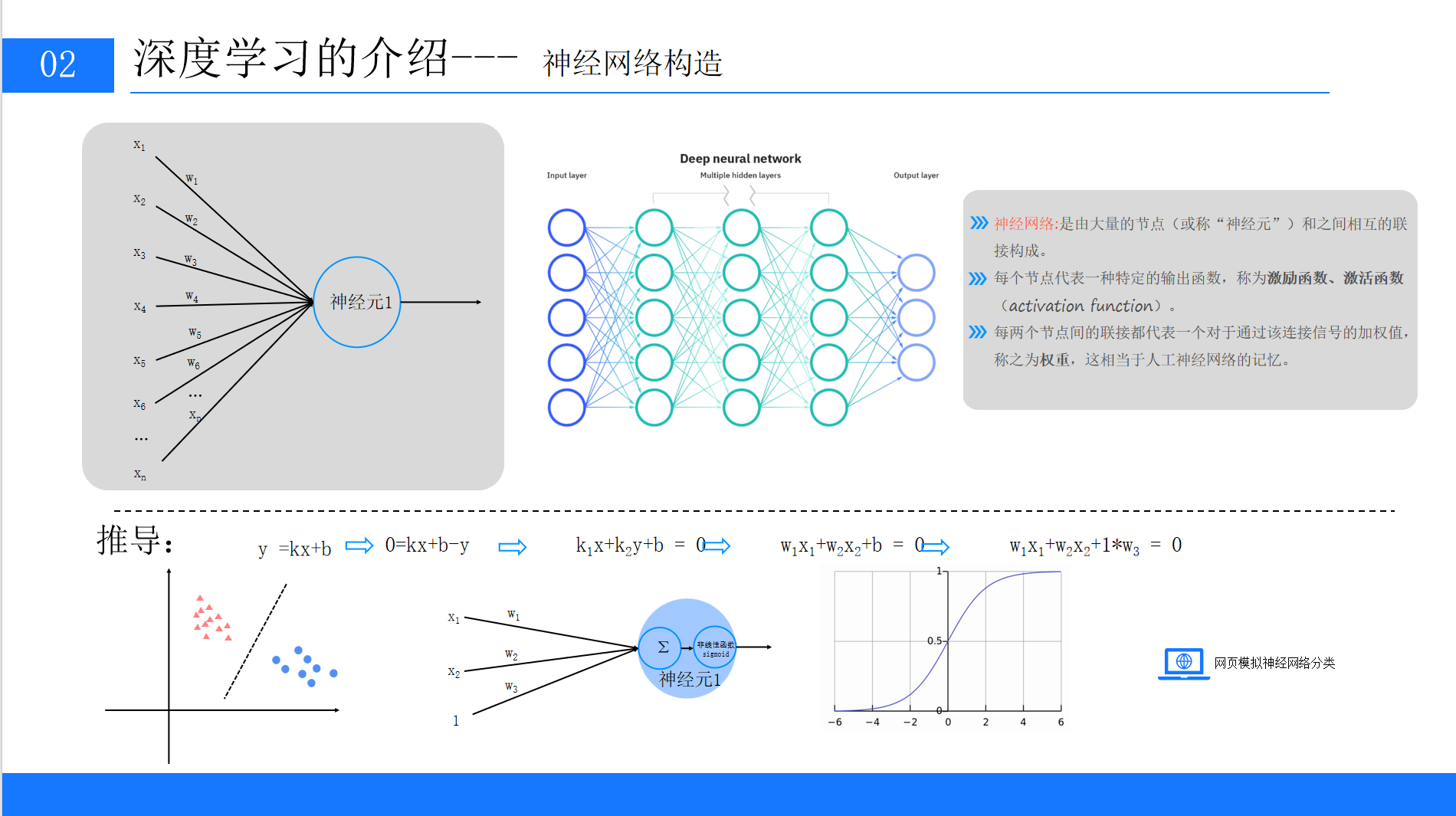
2.2 神经网络：深度学习的核心载体

神经网络是深度学习的核心模型，其灵感来源于人类大脑中神经元的连接方式。神经网络由大量节点（神经元）和节点之间的连接构成 ，每个节点代表一个输出函数（激活函数），每个连接代表一个权重（相当于模型的"记忆"）。

我们可以用一个形象的比喻理解神经网络：如果将数据处理过程比作工厂的流水线，那么每个神经元就是一个加工站，权重就是加工站之间的传送带强度，激活函数则决定了加工后的产品是否合格。数据从输入层进入，经过多层加工后从输出层输出，最终得到预测结果。

三、神经网络的基本构成：神经元与激活函数

3.1 神经元的数学表达

神经元是神经网络的基本单元，其结构可以追溯到最简单的线性函数。

3.1.1 从线性函数到神经元模型

我们先从初中数学中的线性函数说起：

将其扩展到多变量场景，神经元的输入输出关系可以表示为：

复制代码

其中：

x1,x2,...,xn是输入特征（如图像的像素值、文本的词向量）
w1,w2,...,wn是权重（表示每个输入特征的重要程度）
b是偏置（调整函数的基准值，类似线性函数中的截距）
z是神经元的线性输出

3.1.2 偏置的特殊处理

为了方便计算，通常将偏置b视为一个固定输入为1的权重项，即：

复制代码

这里的wn+1就是偏置b，输入xn+1=1。这种处理让权重和偏置可以统一用矩阵运算表示，简化了计算过程。

3.2 激活函数：引入非线性的关键

线性函数的组合仍然是线性函数，无法处理复杂的非线性问题（如异或问题）。因此，神经元需要通过激活函数对线性输出z进行非线性转换，得到最终输出a：

复制代码

a=g(z)

其中g(⋅)为激活函数。

3.2.1 常用激活函数：sigmoid函数

sigmoid函数是早期神经网络中常用的激活函数，其表达式为：

复制代码

g(z)=1+e−z1

它的特点是将输出压缩到(0,1)区间，适合表示概率值。但缺点是当z过大或过小时，函数梯度接近0，容易导致训练停滞（梯度消失问题）。

3.2.2 激活函数的作用

激活函数的核心作用是为神经网络引入非线性，让模型能够拟合任意复杂的函数关系。没有激活函数的神经网络本质上是一个线性回归模型，无法处理图像、语言等非线性数据。

四、感知器：最简单的神经网络

4.1 感知器的结构

感知器是由两层神经元组成的简单神经网络，包括输入层和输出层（无隐藏层）。它是神经网络的雏形，由Frank Rosenblatt于1957年提出。

4.1.1 感知器的数学表达

假设输入特征为x=[x1,x2,x3]，权重矩阵为W（每行对应一个输出神经元的权重），则感知器的输出为：

复制代码

用矩阵表示为：

复制代码

其中W是2×3的权重矩阵，x是3×1的输入向量，g(⋅)是激活函数。

4.1.2 感知器的局限性

感知器只能解决线性可分问题（如AND、OR逻辑运算），无法解决非线性可分问题（如XOR逻辑运算）。例如，XOR问题中，"0,0"和"1,1"输出0，"0,1"和"1,0"输出1，这些点无法用一条直线分割，因此感知器无法拟合。

4.2 感知器的训练过程

感知器的训练目标是找到合适的权重W，使预测值尽可能接近真实标签。训练步骤如下：

随机初始化权重W；
输入样本x，计算预测值z=g(W×x)；
计算预测值与真实标签的误差；
根据误差调整权重（例如使用感知器学习规则：）；
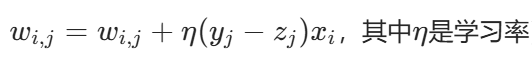重复步骤2-4，直到误差小于阈值或达到最大迭代次数。

五、多层感知器：突破线性限制的神经网络

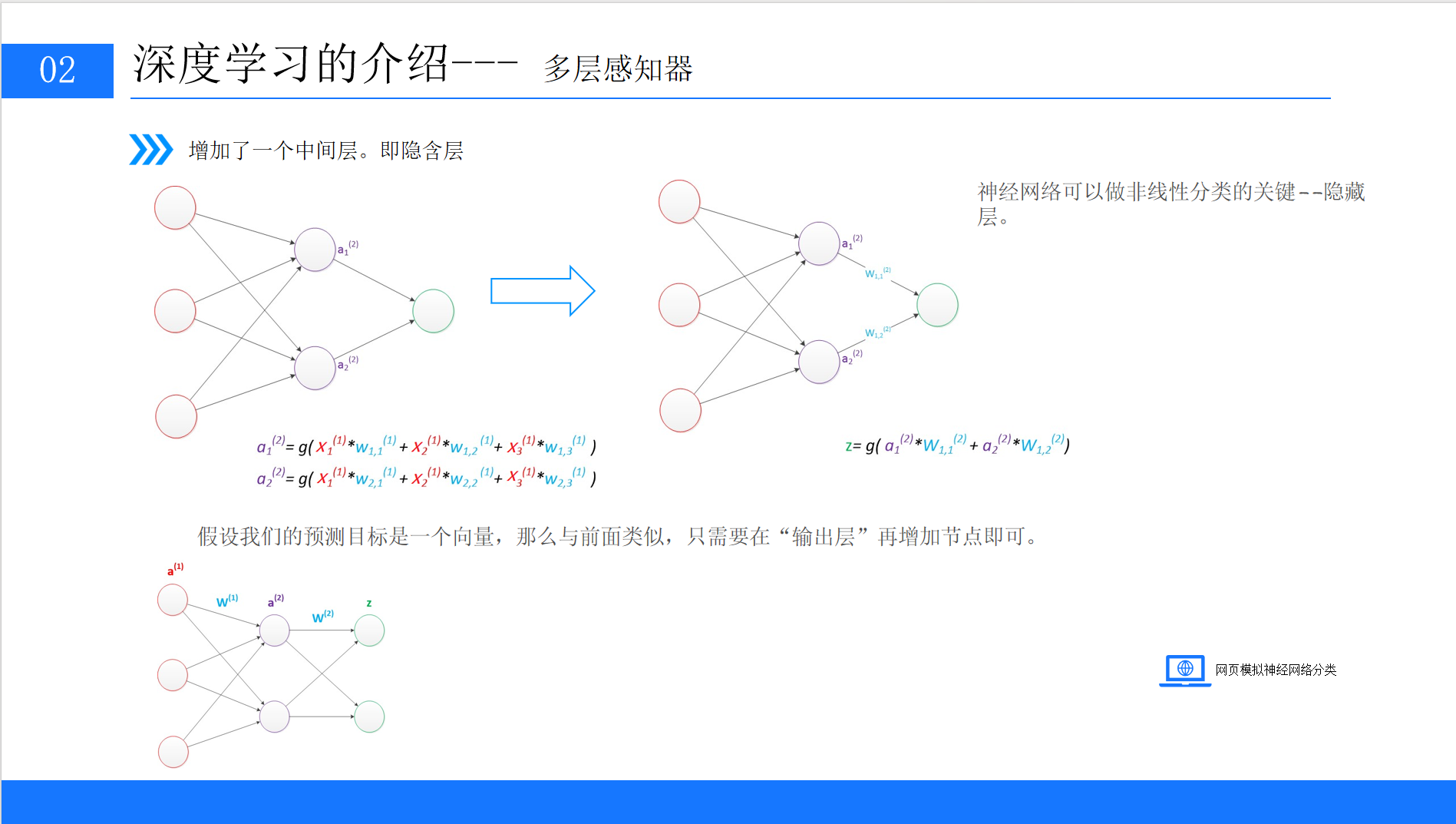
5.1 隐藏层的引入

为了解决感知器无法处理非线性问题的局限，科学家们引入了隐藏层，形成了多层感知器（Multi-Layer Perceptron，MLP）。多层感知器至少包含三层：输入层、隐藏层、输出层。

5.1.1 隐藏层的作用

隐藏层可以对输入特征进行多次非线性转换，从而拟合复杂的函数关系。例如，XOR问题可以通过一个包含2个神经元的隐藏层解决：

隐藏层将输入特征转换为线性可分的新特征；
输出层基于新特征进行分类。

可以说，隐藏层是神经网络实现非线性分类的核心。

5.1.2 多层感知器的数学表达

假设输入层为x=[x1,x2]，隐藏层有2个神经元，输出层有1个神经元，则：

隐藏层输出：
复制代码
输出层输出：
复制代码
其中上标表示层数，w(l)表示第l层的权重，b(l)表示第l层的偏置。

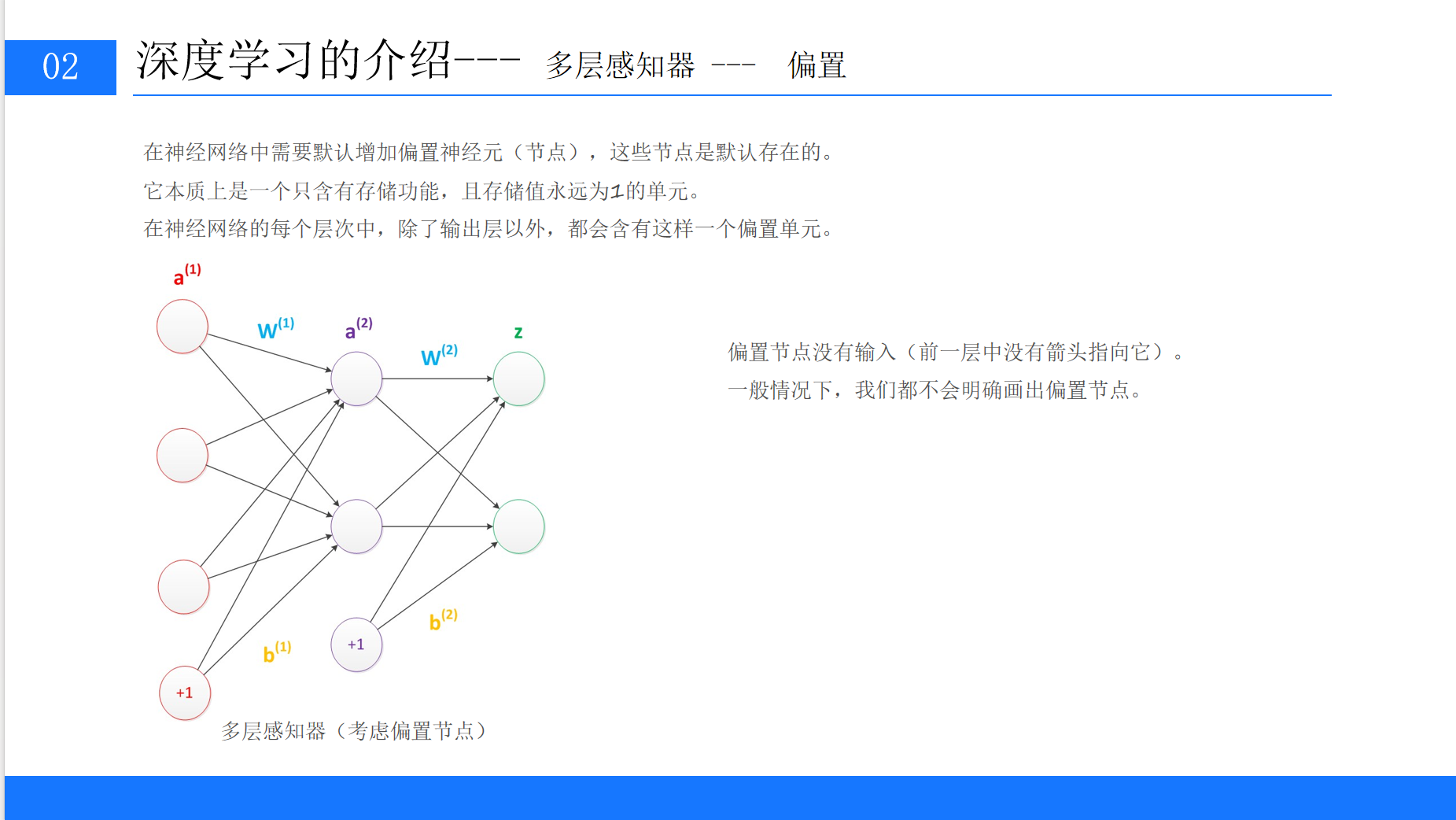
5.2 偏置节点的作用

在神经网络中，除输出层外，每个层都默认包含一个偏置节点，其输出恒为1。偏置节点的作用是：

为每个神经元的线性输出提供一个基准偏移，类似线性函数中的b；
增强模型的灵活性，让函数可以上下平移，更好地拟合数据。

偏置节点没有输入（即前一层没有连接到它的权重），其值固定为1，在计算时通常不单独画出，但必须纳入公式计算。

5.3 中间层节点数的设计

输入层和输出层的节点数由任务决定（输入层节点数=特征维度，输出层节点数=目标维度），但中间层（隐藏层）的节点数没有统一的理论指导，通常根据经验设计：

经验法：隐藏层节点数介于输入层和输出层之间，例如取输入层节点数的2/3或1.5倍；
实验法：预先设定多个候选值（如32、64、128），通过实验对比模型性能，选择最优值；
参考类似任务：借鉴同类型问题的经典模型结构，例如图像分类任务常用128、256等节点数。

节点数过少可能导致模型欠拟合（无法捕捉数据规律），过多则可能导致过拟合（过度拟合训练数据，泛化能力差），需要结合正则化等方法平衡。

六、模型训练的核心：损失函数与正则化

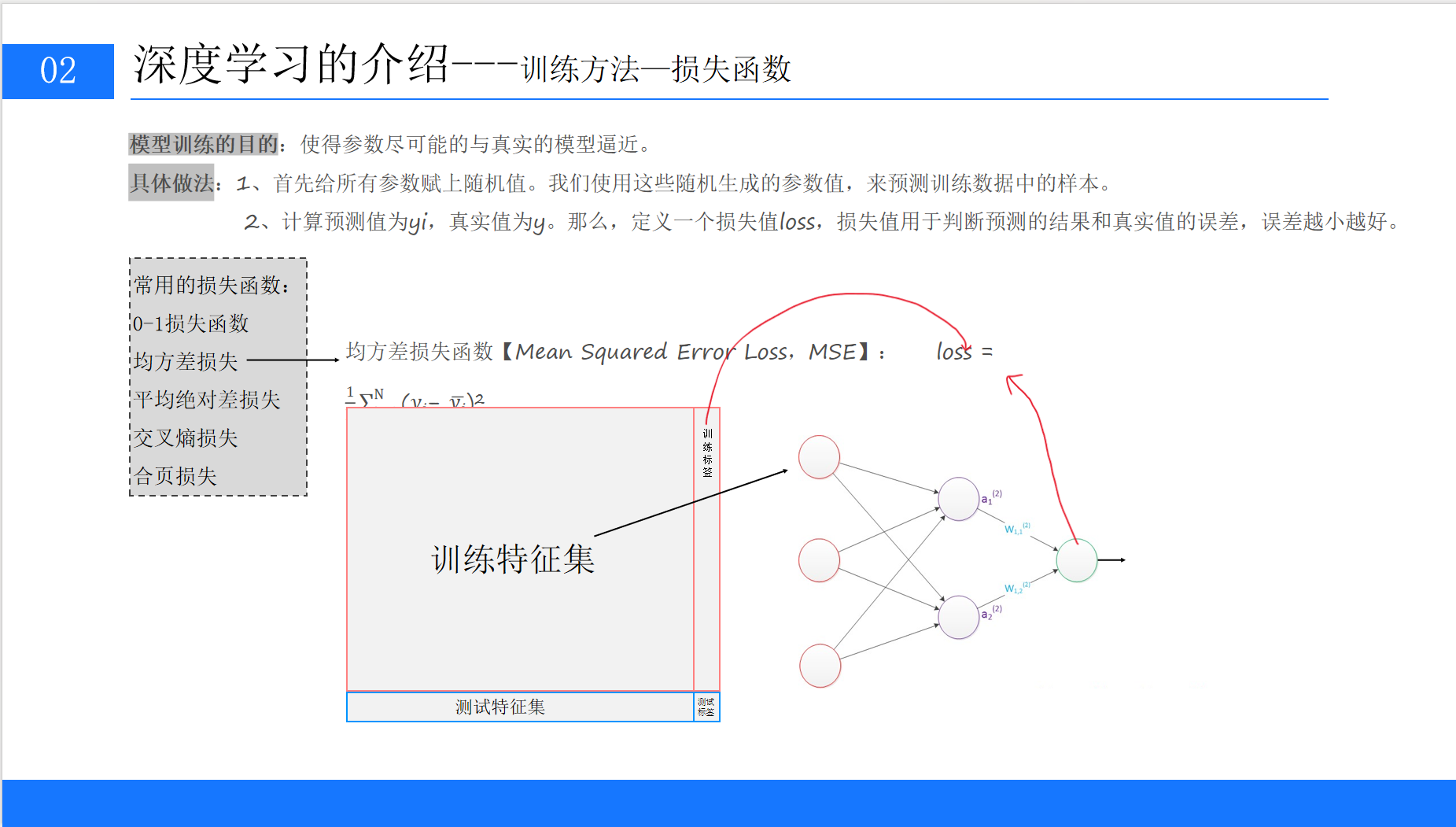
6.1 损失函数：衡量预测误差的指标

模型训练的目标是最小化预测值与真实值的误差，损失函数（Loss Function）就是衡量误差的指标。常用的损失函数包括：

6.1.1 0-1损失函数

复制代码

直接判断预测是否正确，适合分类任务，但因不连续、不可导，很少用于训练。

6.1.2 均方差损失（MSE）

复制代码

计算预测值与真实值的平方差均值，适合回归任务（如房价预测、温度预测）。

6.1.3 交叉熵损失

复制代码

适合分类任务，尤其在多分类中表现优异。它通过衡量两个概率分布（真实标签的分布和预测概率的分布）的差异来计算损失。

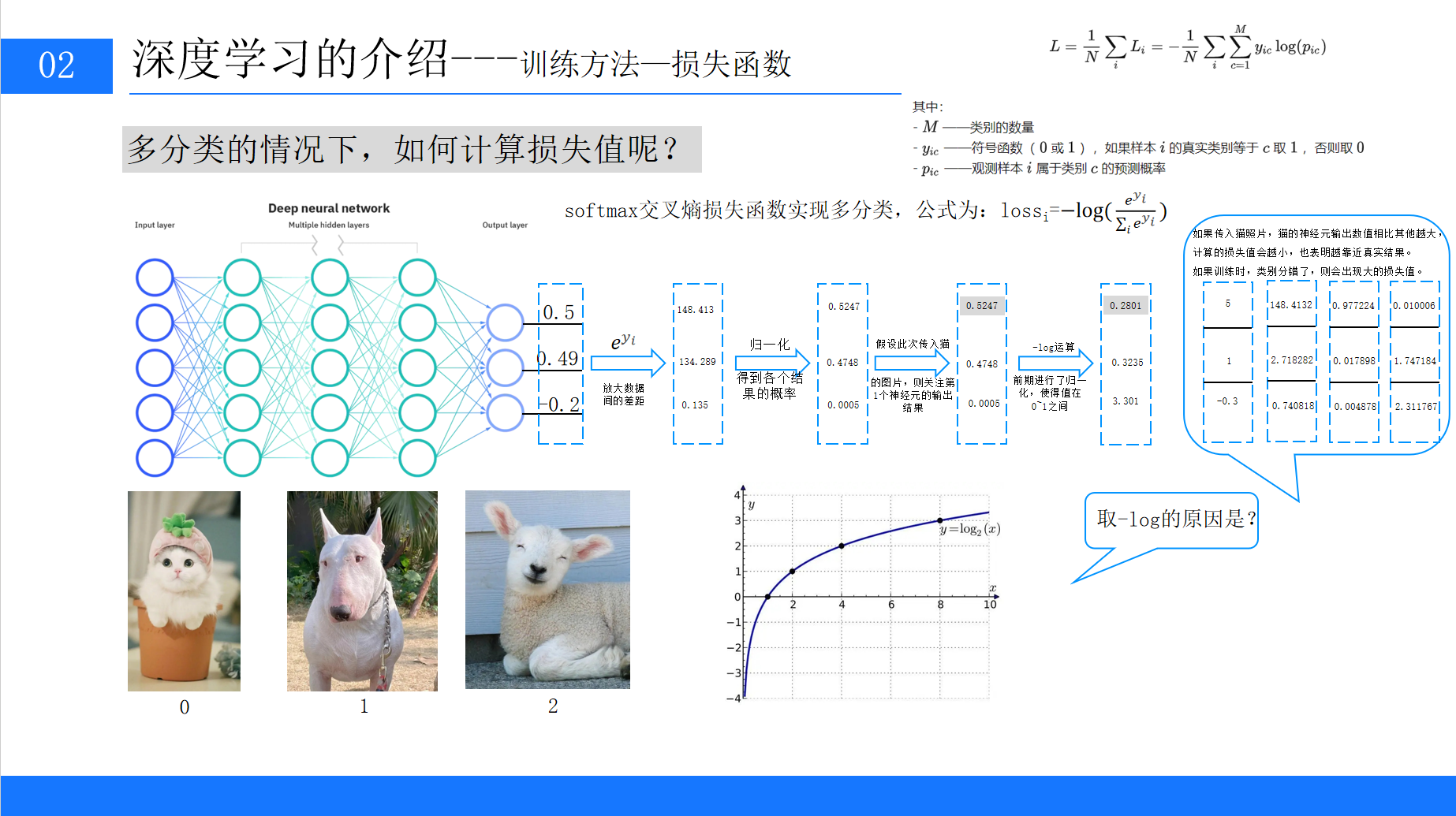
6.2 多分类任务的损失计算

在多分类任务中（如识别猫、狗、鸟），输出层节点数等于类别数，每个节点输出对应类别的概率（通过softmax函数归一化）。

例如，输入一张猫的图片，模型输出概率为[0.4748,0.5247,0.0005]（分别对应狗、猫、鸟），真实标签为[0,1,0]（猫为1，其他为0），则交叉熵损失为：

复制代码

损失值越小，说明预测越接近真实标签。

6.3 正则化：防止过拟合的关键

过拟合是指模型在训练数据上表现优异，但在新数据（测试数据）上表现差的现象。正则化通过惩罚过大的权重，防止模型过度依赖训练数据中的噪声，从而提高泛化能力。

6.3.1 L1正则化

复制代码

对权重的绝对值求和，会使部分权重变为0，实现特征选择（保留重要特征，忽略次要特征）。

6.3.2 L2正则化

复制代码

对权重的平方求和，会使权重普遍变小但不为0，让模型"雨露均沾"地利用所有特征，避免过度依赖某几个特征。

6.3.3 正则化的作用示例

假设输入x=[1,1,1,1]，有两组权重：

w1=[1,0,0,0]：仅依赖第一个特征，容易过拟合；
w2=[0.25,0.25,0.25,0.25]：均衡利用所有特征，泛化能力更好。

L2正则化会惩罚w1（平方和为1），而w2的平方和为0.252×4=0.25，惩罚更小，因此模型会倾向选择w2。

七、优化算法：梯度下降与反向传播

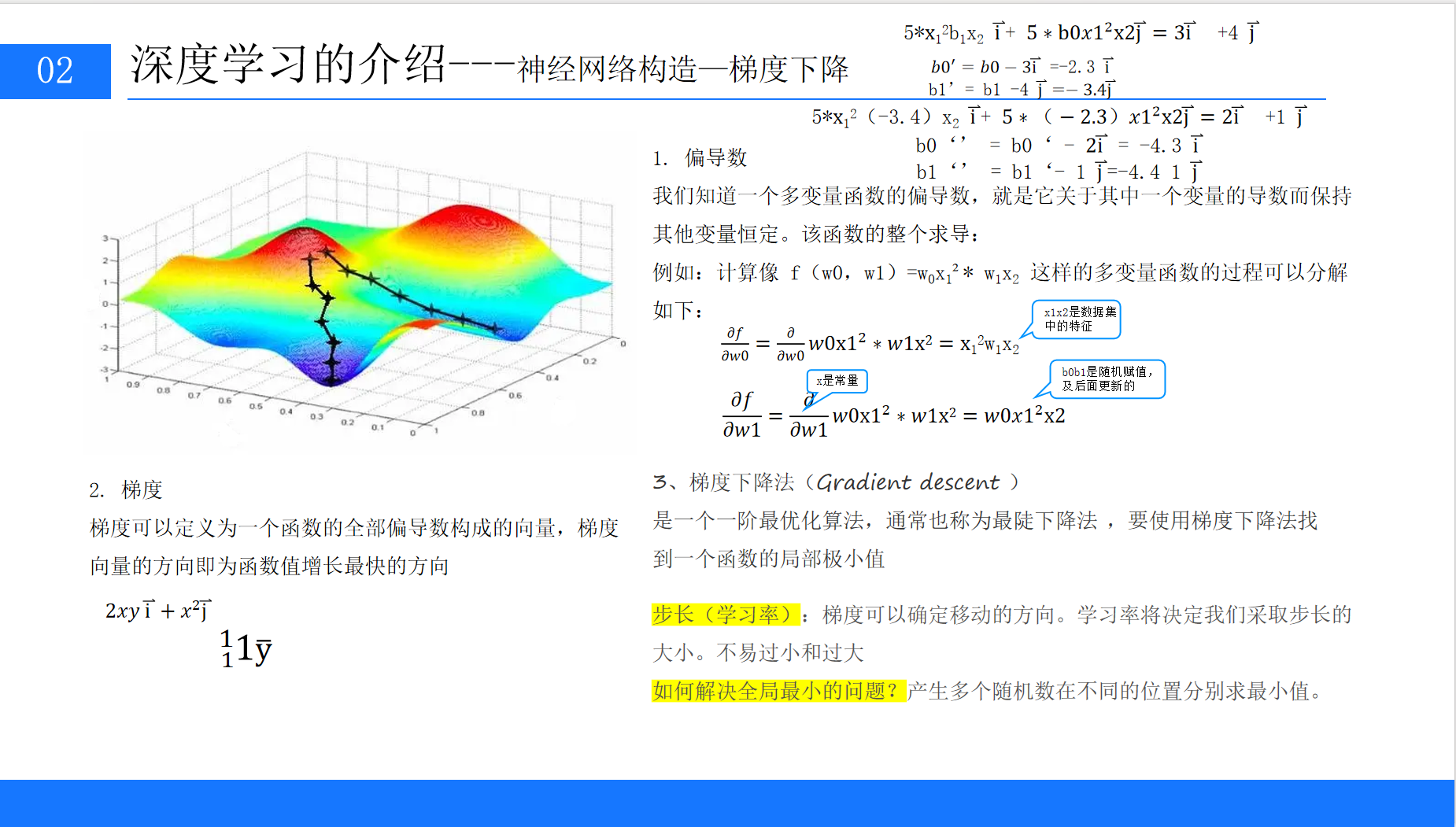
7.1 梯度下降：寻找最优参数的方法

梯度下降是训练神经网络的核心优化算法，其目标是找到使损失函数最小的权重参数。

7.1.1 梯度的概念

梯度是函数所有偏导数构成的向量，其方向是函数值增长最快的方向，反方向则是函数值下降最快的方向。例如，对于函数f(w0,w1)，梯度为：

复制代码

7.1.2 梯度下降的步骤

随机初始化权重w；
计算损失函数关于w的梯度∇L(w)；
沿梯度反方向更新权重：w=w−η∇L(w)（η为学习率，即步长）；
重复步骤2-3，直到损失函数收敛（变化小于阈值）。

7.1.3 学习率的选择

学习率η是关键超参数：

过小：收敛速度慢，需要更多迭代次数；
过大：可能跳过最优解，导致损失函数震荡甚至发散。

实际应用中，通常采用动态学习率（如初始较大，随迭代逐渐减小）。

7.2 BP神经网络：误差反向传播算法

多层感知器的训练需要通过反向传播（Back Propagation，BP） 算法实现，其核心是利用链式法则计算损失函数对各层权重的梯度。

7.2.1 BP算法的步骤

正向传播：输入样本，计算各层输出，得到最终预测值yp；
计算损失：根据预测值yp和真实标签y，计算损失函数L；
反向传播：从输出层开始，逐层计算损失函数对权重的梯度（利用链式法则）；
更新权重：根据梯度和学习率，更新所有层的权重；
循环迭代：重复步骤1-4，直到损失函数达到预设阈值。

7.2.2 链式法则的应用

以两层神经网络为例，输出层权重w(2)的梯度计算为：

复制代码

其中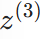是输出层的线性输出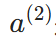，是隐藏层的输出。通过链式法则，将高层的误差"反向传播"到低层，实现所有权重的更新。

八、深度神经网络：从理论到实践

8.1 深度神经网络的特点

当神经网络包含多个隐藏层时，就称为深度神经网络。与浅层网络相比，深度网络的优势在于：

自动特征提取：通过多层非线性转换，自动学习从低级到高级的特征（如从像素→边缘→部件→物体）；
更强的拟合能力：理论上，足够深的网络可以拟合任意复杂的函数；
数据驱动：随着数据量的增加，深度网络的性能会持续提升。

8.2 典型案例：ChatGPT的背后

以ChatGPT为例，它基于1750亿参数的深度神经网络，训练数据包含8000亿个单词（45TB文本）。其强大性能来源于：

超大参数规模：1750亿个权重参数(即w)，能够捕捉语言中的细微规律；
海量训练数据：覆盖互联网文本、书籍、论文等，让模型学习到丰富的知识；
优化的网络结构：基于Transformer架构，通过自注意力机制捕捉长距离依赖关系。

这表明，深度神经网络的性能不仅依赖于结构设计，还与数据量和计算资源密切相关。

8.3 深度学习框架的选择

实际开发中，我们通常使用成熟的深度学习框架搭建模型，常用框架包括：

TensorFlow：Google推出，生态完善，适合生产环境；
PyTorch：Facebook推出，动态图机制，适合科研和快速迭代；
Keras：基于TensorFlow的高层API，简洁易用，适合入门。

这些框架封装了底层的矩阵运算和梯度计算，让开发者可以专注于模型结构设计。

九、总结与学习路径

9.1 核心知识点回顾

本文从基础概念出发，介绍了深度学习的核心内容：

深度学习是机器学习的分支，通过神经网络自动学习特征；
神经元由线性组合和激活函数构成，引入非线性转换；
感知器是简单的两层网络，多层感知器通过隐藏层解决非线性问题；
损失函数衡量误差，正则化防止过拟合，梯度下降和反向传播实现参数优化。

9.2 学习建议

打好数学基础：线性代数（矩阵运算）、微积分（梯度、链式法则）、概率论（损失函数）是深度学习的基石；
动手实践：通过PyTorch或TensorFlow实现简单模型（如MNIST手写数字识别），理解训练过程；
研究经典论文：从LeNet、AlexNet等经典网络入手，逐步深入到Transformer等前沿模型；
关注应用场景：结合具体领域（如计算机视觉、自然语言处理）学习，明确学习目标。

深度学习是一个快速发展的领域，新模型、新算法层出不穷，但核心原理始终围绕神经网络的构建与训练。希望本文能帮助你迈出深度学习的第一步，在实践中不断探索和进步！