2025-08-24：吃披萨。用go语言，给出一个长度为 n 的整数数组 pizzas，pizzas[i] 表示第 i 个披萨的重量。每一天必须恰好取出 4 个

2025-08-24：吃披萨。用go语言，给出一个长度为 n 的整数数组 pizzas，pizzas[i] 表示第 i 个披萨的重量。每一天必须恰好取出 4 个披萨来食用，并把这 4 个披萨按重量从小到大排成 a ≤ b ≤ c ≤ d：

若是第 1、3、5... 天（奇数天），当天的体重增加值为 d（这四个中最重的那块）。
若是第 2、4、6... 天（偶数天），当天的体重增加值为 c（这四个中第二重的）。要求将所有披萨分成 n/4 组四个为一组（每个披萨只能用一次），并确定各组的食用顺序，使得累计的体重增加值最大化。已知 n 为 4 的倍数。求这个最大可能的总增加量。

4 <= n == pizzas.length <= 2 * 100000。

1 <= pizzas[i] <= 100000。

n 是 4 的倍数。

输入： pizzas = [1,2,3,4,5,6,7,8]。

输出： 14。

解释：

第 1 天，你吃掉下标为 [1, 2, 4, 7] = [2, 3, 5, 8] 的披萨。你增加的重量为 8。

第 2 天，你吃掉下标为 [0, 3, 5, 6] = [1, 4, 6, 7] 的披萨。你增加的重量为 6。

吃掉所有披萨后，你增加的总重量为 8 + 6 = 14。

题目来自力扣3457。

解决思路

排序披萨：首先将披萨按重量从大到小排序。这样我们可以优先考虑重量大的披萨，因为它们可能贡献更多的增加值。
分组策略 ：总共有 days = n/4 天（即组数）。为了最大化总增加量，我们需要让奇数天分配到尽可能大的最大值（d），偶数天分配到尽可能大的次大值（c）。
奇数天和偶数天的分配 ：
- 奇数天（第1、3、5...天）直接取最大的那些值作为d（即每组最大值）。因为奇数天直接取最大值，所以我们可以直接取排序后最大的前 odd = (days+1)/2 个披萨（这些将作为奇数天的最大值）。
- 偶数天（第2、4、6...天）需要取次大值（c）。但次大值不能直接取最大的那些（因为最大值已经被奇数天占用了），而是需要从剩余的披萨中挑选较大的次大值。
具体分配方法 ：
- 排序后，最大的前 odd 个披萨（即排序后的前 odd 个）被分配给奇数天作为最大值（d）。
- 对于偶数天，我们需要为每组分配一个次大值（c）。这些次大值应该尽可能大，但必须避免与奇数天冲突（即不能重复使用披萨）。
- 实际上，我们可以通过间隔选取的方式：从排序后的数组中，在跳过前 odd 个之后，每隔一个取一个披萨（即取索引为 odd+1, odd+3, odd+5... 的披萨），共取 days/2 个。这些被选取的披萨将作为偶数天的次大值（c）。
为什么这样分配？ ：
- 奇数天直接取最大的前 odd 个披萨，这显然是最优的（因为奇数天直接取最大值，所以最大的几个必须分配给奇数天）。
- 对于偶数天，我们需要次大值（c）尽可能大。但每组由4个披萨组成，最大值（d）已经很大（通常比c大），所以c不能太大（否则会浪费成为d的机会）。实际上，我们希望c尽可能大，但又不能占用那些可能成为更大d的披萨（即前odd个）。
- 排序后，数组从大到小排列。前odd个已经被用作奇数天的d。接下来，我们考虑剩余披萨中较大的那些作为偶数天的c。但如果我们直接取剩余最大的（即索引odd处的披萨），那么它可能应该作为某个组的d（但奇数天已经用完d名额），所以它只能作为c？但注意：实际上，每个组需要4个披萨，而且d和c来自同一组。
- 更深入的解释：为了最大化总增加量，我们应该让奇数天的d尽可能大（所以取前odd个最大的），然后让偶数天的c尽可能大（但不能影响奇数天的d）。实际上，偶数天的c应该从排序后的数组中"间隔"选取：因为如果我们取索引odd（即第odd+1大的披萨）作为某个偶数天的c，那么它所在的组必须有一个比它更大的d（但这个d已经被奇数天占用了，所以这个组不能是偶数天？）。实际上，我们需要为偶数天构造组，使得c尽可能大，同时d更大（但d已经被奇数天占用了，所以偶数天的d必须比c大，但可能小于奇数天的d）。
- 实际上，算法中偶数天取的c是排序后数组中的索引为 odd+1, odd+3, odd+5... 的元素。这样做的原因是：这些位置的值足够大（因为数组已排序），而且通过间隔选取，可以确保每个偶数天组有一个更大的d（这个d来自前odd个中的某个，但前odd个已经分配给奇数天了？）------这里需要更仔细的构造。
- 实际上，分组是隐含的：我们并不显式构造每组4个披萨，而是直接计算总和。因为问题只要求总和最大化，并不需要输出分组方案。所以算法直接选取了贡献值（奇数天的d和偶数天的c）并求和。

详细步骤（以输入[1,2,3,4,5,6,7,8]为例）

排序披萨：从大到小排序后得到 [8,7,6,5,4,3,2,1]。
计算天数：days = 8/4 = 2。
- 奇数天个数：odd = (2+1)/2 = 1（即第1天是奇数天）。
- 偶数天个数：days/2 = 1（即第2天是偶数天）。
选取奇数天的d：取前odd=1个最大的披萨，即8。
选取偶数天的c：从索引odd=1开始（即跳过前1个），每隔一个取一个，共取days/2=1个：
- 起始索引：odd=1（即第2个元素，值为7）。
- 但算法中取的是 odd + i*2 + 1？实际上，代码中循环是 for i in range(days/2)，取索引为 odd + i*2 + 1。
- 对于i=0：索引 = 1 + 0*2 + 1 = 2（即第3个元素，值为6）。
- 所以取的是6（而不是7）。
总增加量 = 8 + 6 = 14。

为什么取索引2（值为6）而不是索引1（值为7）？

因为如果取索引1（7）作为偶数天的c，那么它所在的组需要有一个比7更大的d（至少为8）。但最大的d（8）已经被奇数天占用了，所以这个组不能是偶数天？实际上，我们需要避免冲突。
更一般地，这种间隔选取方式确保了每个偶数天的c对应的组有一个更大的d（这个d来自前odd个），并且不会重复使用披萨。

总结

算法通过排序和贪心策略，直接选取贡献值（奇数天的最大值和偶数天的次大值）求和，得到最大总增加量。
时间复杂度：排序时间复杂度为 O(n log n)，后续的遍历为 O(n)，因此总时间复杂度为 O(n log n)。
空间复杂度：排序可能使用 O(log n) 的额外空间（如快速排序的递归栈），因此总额外空间复杂度为 O(log n)。

注意

该算法不需要显式构造分组方案，而是通过数学推导直接计算最优和。这种方法的正确性基于贪心选择：让奇数天分配最大的那些值作为d，偶数天分配尽可能大（但又不与奇数天冲突）的值作为c。间隔选取（跳过一些值）是为了确保分组可行（即每个组有4个披萨且不重复使用）。

Go完整代码如下：

go 复制代码

package main

import (
	"fmt"
	"slices"
)

func maxWeight(pizzas []int) (ans int64) {
	slices.SortFunc(pizzas, func(a, b int) int { return b - a })
	days := len(pizzas) / 4
	odd := (days + 1) / 2
	for _, x := range pizzas[:odd] {
		ans += int64(x)
	}
	for i := range days / 2 {
		ans += int64(pizzas[odd+i*2+1])
	}
	return
}

func main() {
	pizzas := []int{1,2,3,4,5,6,7,8}
	result := maxWeight(pizzas)
	fmt.Println(result)
}

Python完整代码如下：

python 复制代码

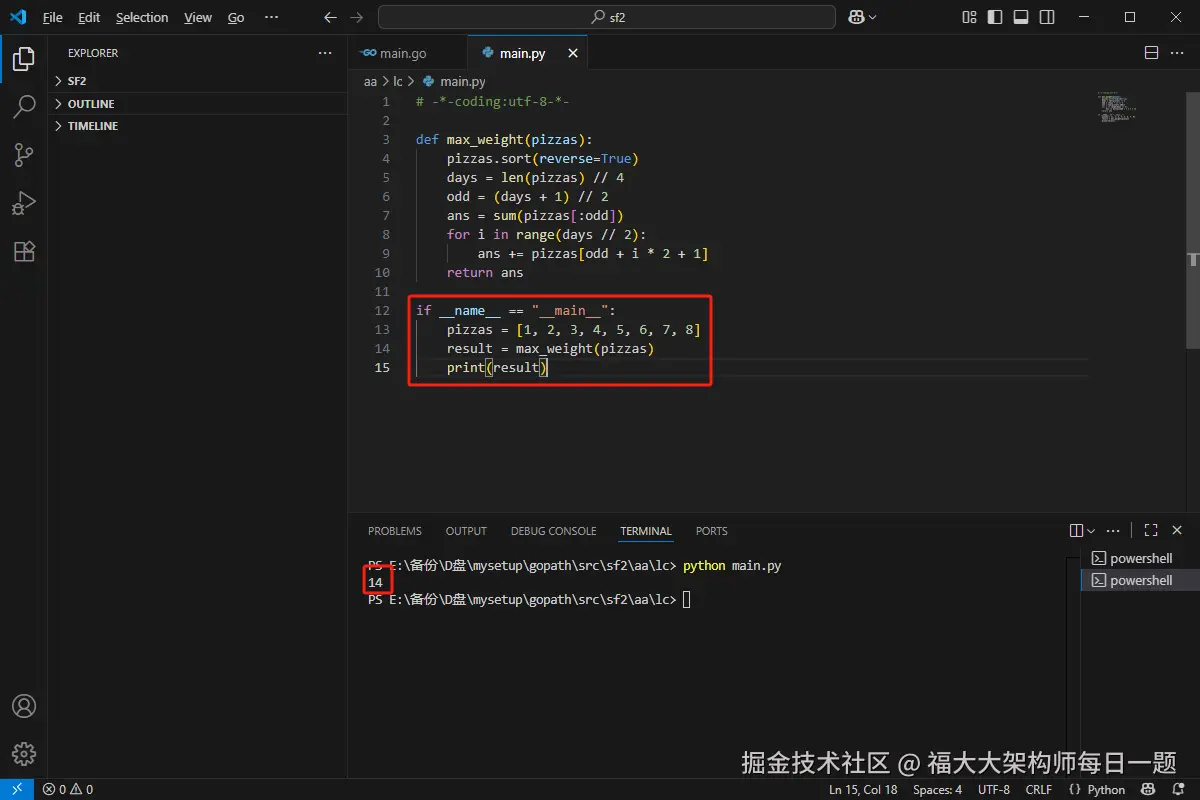
# -*-coding:utf-8-*-

def max_weight(pizzas):
    pizzas.sort(reverse=True)
    days = len(pizzas) // 4
    odd = (days + 1) // 2
    ans = sum(pizzas[:odd])
    for i in range(days // 2):
        ans += pizzas[odd + i * 2 + 1]
    return ans

if __name__ == "__main__":
    pizzas = [1, 2, 3, 4, 5, 6, 7, 8]
    result = max_weight(pizzas)
    print(result)