时间序列分析的集成学习方法

1. 引入.

在本专栏的前两个文章，叙述了如何使用经典统计模型ARIMA来对时间序列进行分解预测，并加入STI分解增加可解释性。在第二篇中，我们列举了ARIMA模型的一些缺点，对于ARIMA的模型参数难以确定一点，我们引入了网格搜索寻优的方式来改进，并介绍了pmdarima库来自动寻参。ARIMA的第二个缺点：要求时间序列平稳，并且不能预测长期的时间数据，灵活性较差，对此，我们可以采用机器学习的方法来改善。

1.1 机器学习方法对于ARIMA的优势

• 特征工程灵活性

机器学习模型允许更复杂的特征工程，并且可以自由设定可能影响的特征，例如通过滞后特征、移动平均特征等捕捉时间序列的动态特性。这种灵活性使得模型能更精准地适应数据中的非线性关系和复杂模式。

• 长期依赖处理能力

LSTM 等深度学习模型通过门控机制（如遗忘门、输入门）有效缓解了长序列中的梯度消失问题，能够捕捉更长的历史依赖关系。而ARIMA模型受限于差分操作，对长期趋势的建模能力相对较弱。

• 复杂场景适应性

机器学习模型（如XGBoost、LightGBM）在处理非平稳时间序列时更具优势。它们能通过梯度提升算法动态调整模型参数，适应数据中的季节性波动、突变点等复杂特性。相比之下，ARIMA模型需通过差分操作将非平稳数据转化为平稳序列，可能丢失部分信息。

• 模型优化效率

机器学习模型支持更高效的参数优化策略（如梯度下降、随机梯度下降），在训练速度和资源消耗上通常优于ARIMA的迭代计算方式。此外，机器学习模型可通过交叉验证等手段提升模型泛化能力。

• 预测精度提升

在处理高维时间序列数据时，机器学习模型能自动提取高阶特征（如周期性、趋势性），而ARIMA依赖人工设定差分阶数和参数。实验表明，在金融、气象等场景中，机器学习模型的预测精度普遍优于传统统计模型。

2. 集成学习模型简介.

集成学习（Ensemble Learning）是一种通过结合多个基学习器的预测结果来提高模型性能的机器学习方法。其核心思想是通过组合多个弱学习器（Weak Learner）的预测结果，生成一个更强大、更稳定的模型。集成学习通常能显著降低模型的方差（Variance）或偏差（Bias），从而提升泛化能力。集成学习主要分为：Bagging、Boosting和Stacking三类，本文主要使用bagging和boosting方法来演示，其每个模型的详细原理将在后续专栏中讲解。

2.1随机森林原理概述

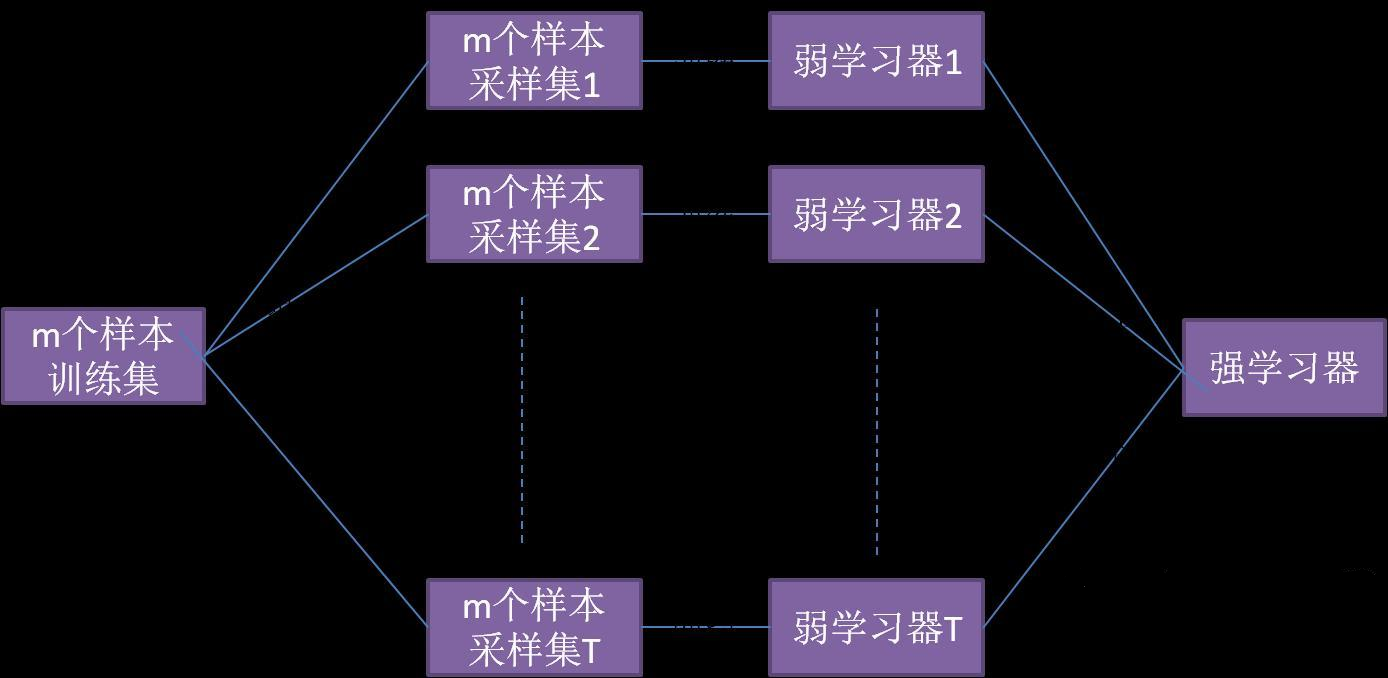
图1：随机森林算法演示图

随机森林是一种基于决策树的集成学习模型，它通过构建多个决策树并综合其结果来提高预测性能。其核心思想是利用 bootstrap 抽样技术从原始数据集中抽取多个样本集，为每个样本集构建一棵决策树，在构建过程中，每个节点分裂时仅从随机选择的部分特征中选取最优特征，最后通过投票（分类问题）或平均（回归问题）的方式得到最终结果。

损失函数 ：随机森林在分类问题中常用的损失函数为分类误差，即错分样本数占总样本数的比例；在回归问题中常用均方误差（MSE），公式为，其中为真实值，为预测值，为样本数量。

迭代公式 ：随机森林不存在显式的迭代公式，它是通过并行构建多棵独立的决策树，最终综合各树结果，即（回归问题），其中为决策树数量，为第棵决策树的预测函数。

算法步骤：

1. 从原始数据集中，通过 bootstrap 抽样方法随机抽取个样本集。
2. 对于每个样本集，构建一棵决策树，在构建过程中，每个节点分裂时随机选择部分特征，从这些特征中选择最优分裂点。
3. 重复步骤 2，构建棵决策树。
4. 对于新的输入样本，将其输入到每棵决策树中得到预测结果，通过投票（分类）或平均（回归）得到最终预测结果。

2.2 Adaboost 原理概述

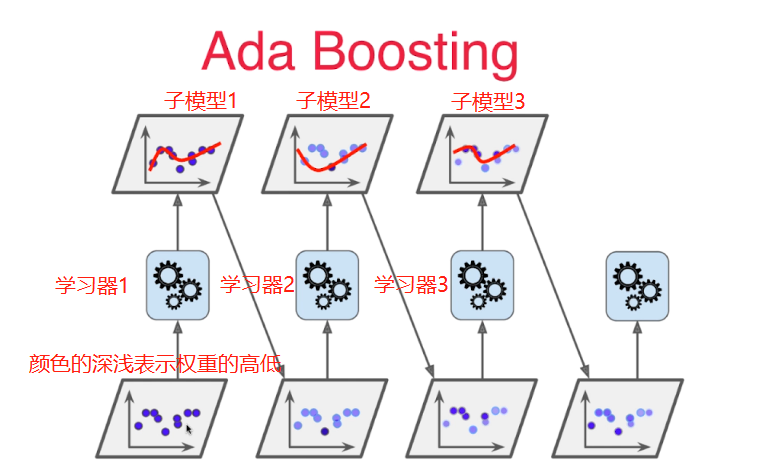
图2：Adaboost演示图

Adaboost（自适应增强）是一种迭代式的集成学习算法，它通过不断调整样本权重，聚焦于难以分类的样本，最终将多个弱分类器组合成一个强分类器。

损失函数 ：Adaboost 在二分类问题中常用指数损失函数，公式为，其中为真实标签，为分类器的预测值。

迭代公式：

• 样本权重更新：，其中为第轮中第个样本的权重，为第个弱分类器的权重，为第个弱分类器对第个样本的预测结果，为归一化因子，。

• 弱分类器权重：，其中为第个弱分类器的分类误差率，，为指示函数。

• 最终分类器：，其中为弱分类器数量。

算法步骤：

1. 初始化样本权重，令，其中为样本数量，。
2. 对于)到（弱分类器数量）：

• 根据当前样本权重训练一个弱分类器。
• 计算的分类误差率。
• 计算的权重。
• 更新样本权重。

3.构建最终的强分类器。

2.3 GBDT 原理概述

GBDT（梯度提升决策树）是一种基于梯度下降的集成学习算法，它通过迭代地构建决策树，每一棵新的树都用来拟合前序模型的残差（梯度），从而不断减小损失函数。

损失函数 ：GBDT 可根据具体问题选择不同的损失函数，回归问题常用均方误差；分类问题常用对数损失函数，二分类时为，其中为预测概率。

迭代公式：

• 负梯度（残差）：，对于均方误差损失，。

• 模型更新：，其中为步长（学习率），通过线性搜索确定，为第棵决策树。

算法步骤：

1. 初始化模型。
2. 对于到（树的数量）：

• 对每个样本，计算负梯度，将其作为残差的近似。
• 利用样本训练一棵决策树，得到叶子节点区域，其中为叶子节点数量。
• 对于每个叶子节点区域，计算最优步。
• 更新模型。

3. 得到最终模型。

2.4 XGBoost 原理概述

XGBoost（极端梯度提升树）是 GBDT 的一种高效实现，它在 GBDT 的基础上进行了诸多优化，如引入正则化项、支持并行计算等，具有更快的训练速度和更好的泛化性能。

损失函数 ：XGBoost 的损失函数由两部分组成，即训练损失和正则化项，公式为，其中为训练损失函数（如均方误差、对数损失等），为正则化项，为决策树的叶子节点数量，为第个叶子节点的权重，和为正则化参数。

迭代公式：

• 泰勒二阶展开近似损失：，其中，。

• 树结构评分：对于一棵结构为的树，其评分，最优权重，代入后得。

• 模型更新：。

算法步骤：

1. 初始化模型。
2. 对于到（树的数量）：

• 计算每个样本的一阶导数和二阶导数。
• 基于和，使用贪心算法构建决策树，通过计算分裂前后的评分增益选择最优分裂点。
• 计算叶子节点的最优权重。
• 更新模型。

3. 得到最终模型。

2.5 各模型对比表格

|----------|---------------------|------------------------|--------------------|--------------|----------------------|-----------------|
| 模型 | 核心思想 | 损失函数 | 迭代特点 | 并行性 | 正则化 | 对异常值敏感性 |
| 随机森林 | 集成多棵独立决策树，综合结果 | 分类：分类误差；回归：均方误差 | 无显式迭代，并行构建树 | 强，树之间独立 | 通过树的数量和特征抽样实现 | 较低，多棵树综合降低影响 |
| Adaboost | 迭代调整样本权重，聚焦难分样本 | 二分类：指数损失函数 | 串行迭代，每棵树基于前序结果调整权重 | 弱，需按顺序构建树 | 无专门正则化项，通过控制弱分类器数量实现 | 较高，异常值易被赋予高权重 |
| GBDT | 迭代拟合前序模型残差（梯度） | 回归：均方误差；分类：对数损失等 | 串行迭代，每棵树拟合前序残差 | 弱，需按顺序构建树 | 较弱，可通过树深度等控制 | 较高，残差计算易受异常值影响 |
| XGBoost | GBDT 的优化，引入正则化和二阶导数 | 训练损失 + 正则化项（含叶子节点数和权重） | 串行迭代，利用二阶导数优化 | 较强，可并行处理特征分裂 | 强，正则化项控制树复杂度 | 较低，正则化和二阶导数缓解影响 |

3. 演示集成学习在时间序列分析上的应用-基于sklearn

3.1 数据集说明

为了演示集成学习在复杂时间序列场景下的优势，本文将使用2013年的电网负荷数据，其时间颗粒度为天，范围覆盖两年。下面是数据集的时间序列图。

3.2 数据特征挖掘

为了找到该时间序列的特征，我们将会对数据进行分组聚合等操作，并将其可视化以发现可以作为特征的数据。

对于当前小时的电力负荷数据，它可能受所属月份影响（1-12月有用电高峰期和用电低峰期）、可能受所属时段影响（白天用电可能比晚上用电多）、可能受节假日影响（不同节假日用电量不同）、也可能受从它开始往前三个小时时段的电力负荷影响。因此，我们一一进行拆解分析，并作出图像来观察是否有显著区别，其代码如下：

3.2.1导包代码

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

from sklearn.model_selection import train_test_split, GridSearchCV, KFold
from sklearn.preprocessing import StandardScaler

from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, AdaBoostRegressor, GradientBoostingRegressor
import joblib

from sklearn.metrics import mean_squared_error, mean_absolute_error, root_mean_squared_error, mean_absolute_percentage_error

import xgboost as xgb
from sklearn.model_selection import StratifiedKFold

import chinese_calendar as calendar  # 查看中国节假日库
from datetime import datetime
# 设置显示中文.
plt.rcParams['font.sans-serif'] = ['SimHei']
# 显示负号
plt.rcParams['axes.unicode_minus'] = False

3.2.2 读取数据并转换为datetime格式

df_train = pd.read_csv('./data/train.csv')
df_test  = pd.read_csv('./data/test.csv')
df_train.head()

df_train.time = pd.to_datetime(df_train.time,format='%Y/%m/%d %H:%M')
df_train.head()

3.2.3 数据可视化观察

# 查看df_train和df_test时间列节假日名称.
def get_holiday_name(x: datetime) -> str:
    # 如果是节假日, 返回节假日名称.
    if calendar.get_holiday_detail(x)[0]:
        # 如果是普通周末, 返回普通周末.
        if calendar.get_holiday_detail(x)[1] is None:
            return 'weekend'
        else:
            return calendar.get_holiday_detail(x)[1]
    else:
        return 'work day'

# 复制一份数据, 避免修改原数据
data = df_train.copy(deep=True)

# 创建画布
fig = plt.figure(figsize=(20, 32))
# 1.负荷整体的分布情况
ax1 = fig.add_subplot(411)
ax1.hist(data['power_load'], bins=50)
ax1.set_title('负荷分布直方图')

# 2.各个小时的平均负荷趋势，看一下负荷在一天中的变化情况
ax2 = fig.add_subplot(412)
data['hour'] = data['time'].dt.hour
data_hour_avg = data.groupby(by='hour', as_index=False)['power_load'].mean()
ax2.plot(data_hour_avg['hour'], data_hour_avg['power_load'], color='b', linewidth=2)
ax2.set_title('各小时的平均负荷趋势图')
ax2.set_xlabel('小时')
ax2.set_ylabel('负荷')
ax2.grid(True,alpha=0.5)

# 3.各个月份的平均负荷趋势，看一下负荷在一年中的变化情况
ax3 = fig.add_subplot(413)
data['month'] = data['time'].dt.month
data_month_avg = data.groupby('month', as_index=False)['power_load'].mean()
ax3.plot(data_month_avg['month'], data_month_avg['power_load'], color='r', linewidth=2)
ax3.set_title('各月份平均负荷')
ax3.set_xlabel('月份')
ax3.set_ylabel('平均负荷')
ax3.grid(True,alpha=0.5)

# 4. 查看各个节假日的平均负荷情况.
ax5 = fig.add_subplot(414)
data['holiday_name'] = data['time'].apply(get_holiday_name)
power_load_holiday_avg = data.groupby('holiday_name')['power_load'].mean()
ax5.plot(power_load_holiday_avg.index, power_load_holiday_avg.values,color='y',linewidth=2)
ax5.set_title('节假日平均负荷对比')
ax5.set_xlabel('节假日名称')
ax5.set_ylabel('平均负荷')
ax5.grid(True, alpha=0.5)

plt.savefig('./data/负荷分析图.png')
plt.show()

可视化结果如图3：

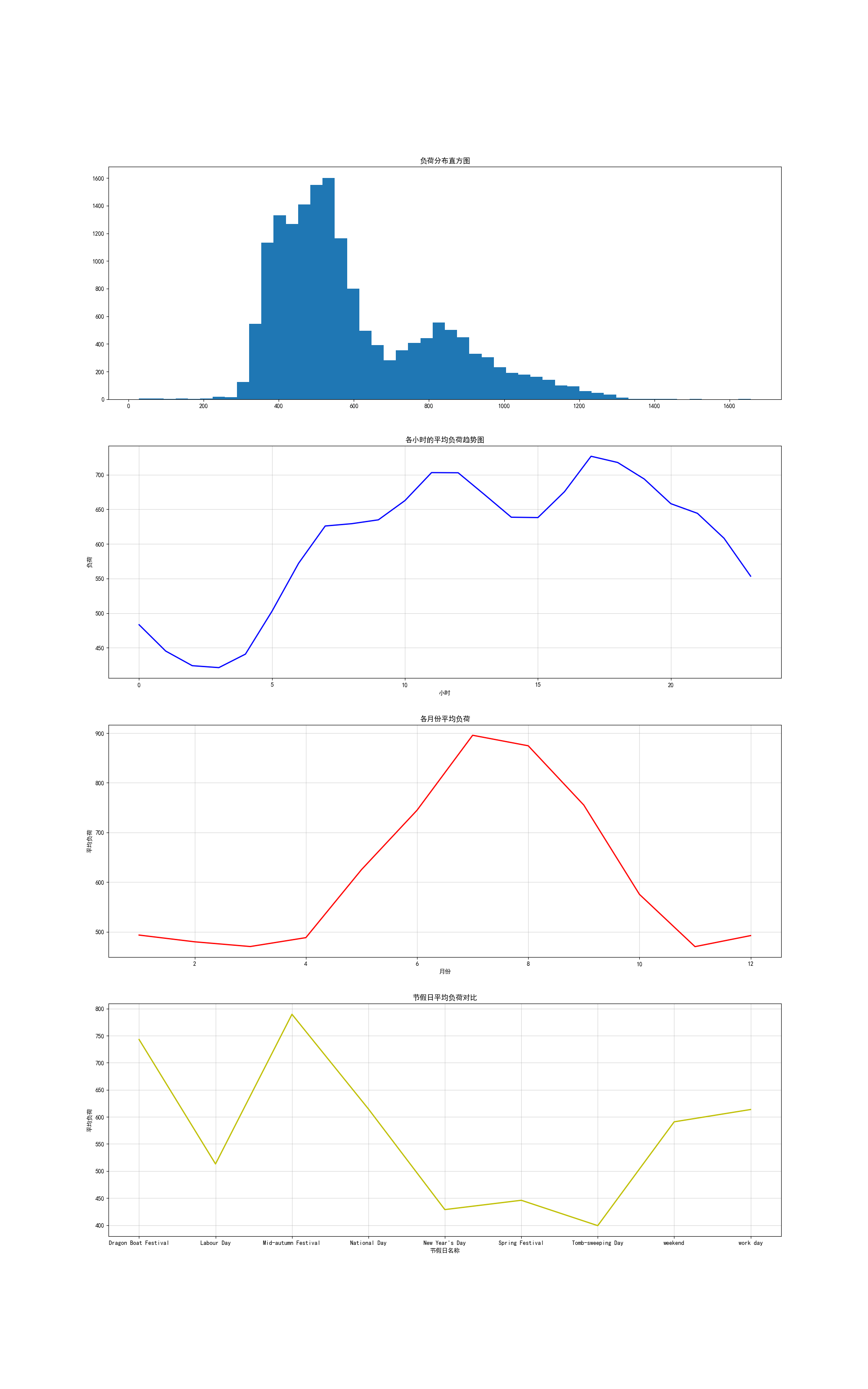
图3：时间序列特征拆解可视化

从可视化结果来看，大部分时段的用电负荷都处于400-600区间；并且与月份有着较强的关系：在6-8月是用电高峰期，而在11-12月是用电低峰期（可能是夏天用空调较多的缘故...）；从一天24小时的时段分布来看，10-14，16-18这个时间段用电较多，而凌晨0-5点用电较少；从节假日时段来看，端午、中秋等节日用电量较多，工作日和寻常周末用电量接近。

从图形可视化结果来看，月份、小时和节假日似乎都是影响较大的指标，可以作为特征列，于是我们进行特征工程部分。

3.3 特征工程

# 1. 分解出以月,周为周期的时间序列以及节假日时间序列.
df_train['month'] = df_train.time.dt.month
df_train['hour']  = df_train.time.dt.hour
df_train['holiday'] = df_train.time.apply(get_holiday_name)

month = pd.get_dummies(df_train['month'])
month_columns = [f'month_{i+1}' for i in range(12)]
month.columns = month_columns

# 2. 分解出以小时为周期的时间序列.
hour = pd.get_dummies(df_train['hour'])
hour_columns = [f'hour_{i}' for i in range(24)]
hour.columns = hour_columns

# 3. 分解出前一个小时、前两个小时和前三个小时的时间序列.
df_train['last_1h'] = df_train['power_load'].shift(1)
df_train['last_2h'] = df_train['power_load'].shift(2)
df_train['last_3h'] = df_train['power_load'].shift(3)

# 4. 分解出前一天同一时间的时间序列.
df_train['last_day'] = df_train['power_load'].shift(24)

# 5. 分解出节假日
holiday = pd.get_dummies(df_train['holiday'])

# 5. 拼接df_train, month, hour, holiday.
df_train = pd.concat([df_train, month, hour, holiday], axis=1)
# 5. 删除空值列.
df_train = df_train.dropna()
df_train.head()

# 对df_test做同样的处理.
# 1. 分解出以月为周期的时间序列.
df_test.time = pd.to_datetime(df_test.time,format='%Y/%m/%d %H:%M')
df_test['hour']  = df_test.time.dt.hour
df_test['month'] = df_test.time.dt.month

row = df_test.shape[0]
month = pd.DataFrame(np.zeros((row, 12)), columns=[f'month_{i+1}' for i in range(12)])
for i in range(row):
    month.iloc[i, df_test.iloc[i]['month']-1] = 1       # 将month列转换为one-hot编码


# 2. 分解出以小时为周期的时间序列.
hour = pd.get_dummies(df_test['hour'])
hour_columns = [f'hour_{i}' for i in hour.columns]
hour.columns = hour_columns

# 3. 分解出前一个小时、前两个小时和前三个小时的时间序列.
df_test['last_1h'] = df_test['power_load'].shift(1)
df_test['last_2h'] = df_test['power_load'].shift(2)
df_test['last_3h'] = df_test['power_load'].shift(3)

# 4. 分解出前一天同一时间的时间序列.
df_test['last_day'] = df_test['power_load'].shift(24)

# 5. 分解出节假日
holiday = pd.DataFrame(np.zeros((row,df_train['holiday'].nunique())), columns=df_train.columns[-9:])
for i in range(row):
    test_holiday_name = get_holiday_name(df_test.iloc[i]['time'])
    holiday.loc[i,test_holiday_name] = 1

# 6. 拼接df_test, month, hour, holiday.
df_test = pd.concat([df_test, month, hour, holiday], axis=1)

# 7. 删除空值列.
df_test = df_test.dropna()
df_test.head()

处理后的特征DataFrame部分展示如图4：

图4：特征工程部分图

处理完之后，剩下就是使用各种集成学习来训练和测试，对比模型的性能。

3.4 模型训练

3.4.1 RandomForest

x_train = df_train.iloc[:, 5:].values   # 注意df_train相比于df_test多了holiday列, 因此要从列号5开始取.
y_train = df_train.iloc[:, 1].values

x_test = df_test.iloc[:, 4:].values
y_test = df_test.iloc[:, 1].values

print(f'训练集的行数: {x_train.shape[0]}')
print(f'训练集的列数: {x_train.shape[1]}')
print(f'测试集的行数: {x_test.shape[0]}')
print(f'测试集的列数: {x_test.shape[1]}')

# 创建 随机森林对象, 并加入网格搜索寻找最优参数
estimator3 = RandomForestRegressor()
# 参数准备.
params = {'n_estimators': [300,325,350], 'max_depth': [7, 9, 11, 12]}
# 创建网格搜索对象 结合 交叉验证.
estimator3_grid = GridSearchCV(estimator3, param_grid=params, cv=5)
# 模型训练.
estimator3_grid.fit(x_train, y_train)
# 模型预测.
y_pred = estimator3_grid.predict(x_test)
# 模型评估.
print('-'*50)
print(f'经网格搜索后的随机森林均方误差: {mean_squared_error(y_test, y_pred)}')
print(f'经网格搜索后的随机森林均方根误差: {np.sqrt(mean_squared_error(y_test, y_pred))}')
print(f'经网格搜索后的随机森林平均绝对误差: {mean_absolute_error(y_test, y_pred)}')
print(f'经网格搜索后的随机森林平均绝对百分比误差: {mean_absolute_percentage_error(y_test, y_pred)}')
print(f'最佳参数为: {estimator3_grid.best_params_}')

# 将训练好的随机森林模型保存在model文件夹下, 命名为RF_model
joblib.dump(estimator3_grid, './model/RF_model.pkl')


# 画出真实图和预测图形.
plt.figure(figsize=(20, 8), dpi=100)

plt.plot(df_test.time, y_test, color='b', label='真实值')      # 画出真实图像.
plt.plot(df_test.time, y_pred, color='y', label='预测值')      # 画出预测图像.

plt.grid(True, alpha=0.5)       # 显示网格
plt.legend()                    # 显示图例
plt.xticks(df_test.time[::24])   # 每隔一天显示一个标签
plt.xticks(rotation=45)         # 旋转45度
plt.xlabel('时间')
plt.ylabel('负荷')
plt.title('随机森林预测结果')
plt.show()

随机森林测试集上真实与预测图如图5：

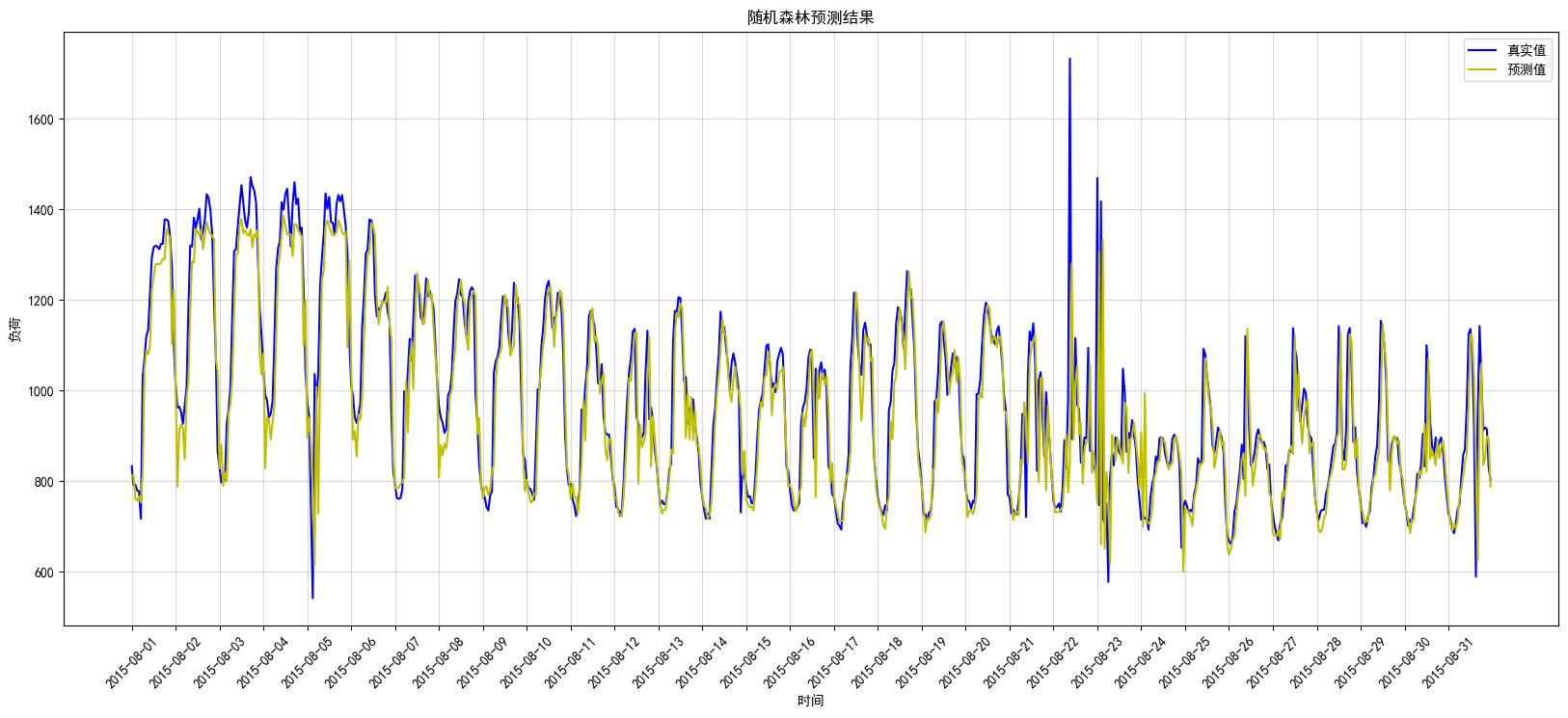
图5：随机森林测试图

从图中可以看出，除了部分突变数据没能拟合上之外，大部分数据都几乎一致，其MSE等指标统一在模型评估上展示。从指标对比上来看，随机森林是比较好的模型。

3.4.2 AdaBoost

# 创建模型对象
# 参1: 弱分类器(决策树对象)
estimator2 = AdaBoostRegressor(estimator=DecisionTreeRegressor(max_depth=np.random.randint(1,10)))

# 设置超参数范围字典.
param_dict = {'n_estimators': [30, 50, 100], 'learning_rate': [0.01,0.05,0.1]}

estimator2_grid = GridSearchCV(estimator2, param_grid=param_dict, cv=5)
# 训练模型
estimator2_grid.fit(x_train, y_train)
# 模型预测
y_pred2 = estimator2_grid.predict(x_test)
# 模型评估
print(f'Adaboost的均方误差: {mean_squared_error(y_test, y_pred2)}')
print(f'Adaboost的均方根误差: {np.sqrt(mean_squared_error(y_test, y_pred2))}')
print(f'Adaboost的平均绝对误差: {mean_absolute_error(y_test, y_pred2)}')
print(f'Adaboost的平均绝对百分比误差: {mean_absolute_percentage_error(y_test, y_pred2)}')
print(f'最佳参数为: {estimator2_grid.best_params_}')
# 保存模型为AdaBoost_model.pkl
joblib.dump(estimator2_grid, './model/AdaBoost_model.pkl')

# 可视化AdaBoost结果.
plt.figure(figsize=(20, 8), dpi=100)
# 真实值图像
plt.plot(df_test.time, y_test, color='b', label='真实值')
# 预测值图像
plt.plot(df_test.time, y_pred2, color='y', label='预测值')

# 设置网格、图例、x轴显示范围
plt.grid(True, alpha=0.5)
plt.legend()
plt.xticks(df_test.time[::24])
plt.xticks(rotation=45)  # 旋转45度

# 添加x轴、y轴和标题
plt.xlabel('时间')
plt.ylabel('负荷')
plt.title('AdaBoost预测结果')
# 显示图像
plt.show()

AdaBoost测试集上真实值与预测值效果图见图6：

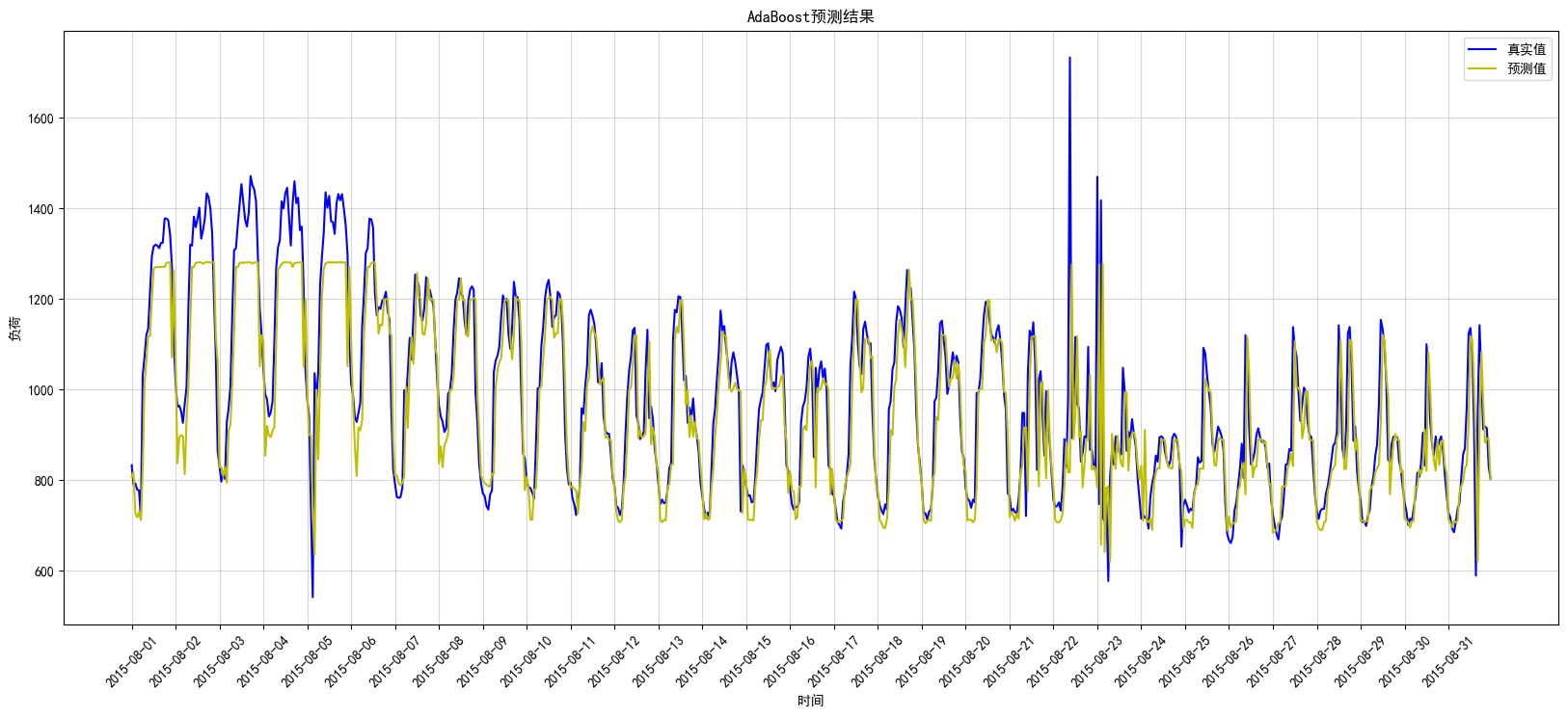图6：AdaBoost测试图

3.4.3 GBDT

# 创建模型对象
estimator1 = GradientBoostingRegressor()

# 设置超参数范围字典.
param_dict = {'n_estimators': [100], 'learning_rate': [0.1], 'max_depth': [7]}    # 这里我是先用了XGBoost来遍历, 选了XGBoost的最优参当作GBDT的参数

# 创建网格搜索对象.
estimator1_grid = GridSearchCV(estimator1, param_grid=param_dict, cv=5)

# 训练模型.
estimator1_grid.fit(x_train, y_train)

# 模型预测.
y_pred3 = estimator1_grid.predict(x_test)

# 模型评估.
print(f'GBDT的均方误差: {mean_squared_error(y_test, y_pred3)}')
print(f'GBDT的均方根误差: {np.sqrt(mean_squared_error(y_test, y_pred3))}')
print(f'GBDT的平均绝对误差: {mean_absolute_error(y_test, y_pred3)}')
print(f'GBDT的平均绝对百分比误差: {mean_absolute_percentage_error(y_test, y_pred3)}')
print(f'最佳参数为: {estimator1_grid.best_params_}')

# 保存模型为GBDT_model.pkl
joblib.dump(estimator1_grid, './model/GBDT_model.pkl')

# 可视化GBDT结果.
plt.figure(figsize=(20, 8), dpi=100)
# 真实值图像
plt.plot(df_test.time, y_test, color='b', label='真实值')
# 预测值图像
plt.plot(df_test.time, y_pred3, color='y', label='预测值')

# 设置网格、图例、x轴显示范围
plt.grid(True, alpha=0.5)
plt.legend()
plt.xticks(df_test.time[::24])
plt.xticks(rotation=45)  # 旋转45度

# 添加x轴、y轴和标题
plt.xlabel('时间')
plt.ylabel('负荷')
plt.title('GBDT预测结果')
# 显示图像
plt.show()

GBDT在测试集上的真实值与预测值比对图见图7：

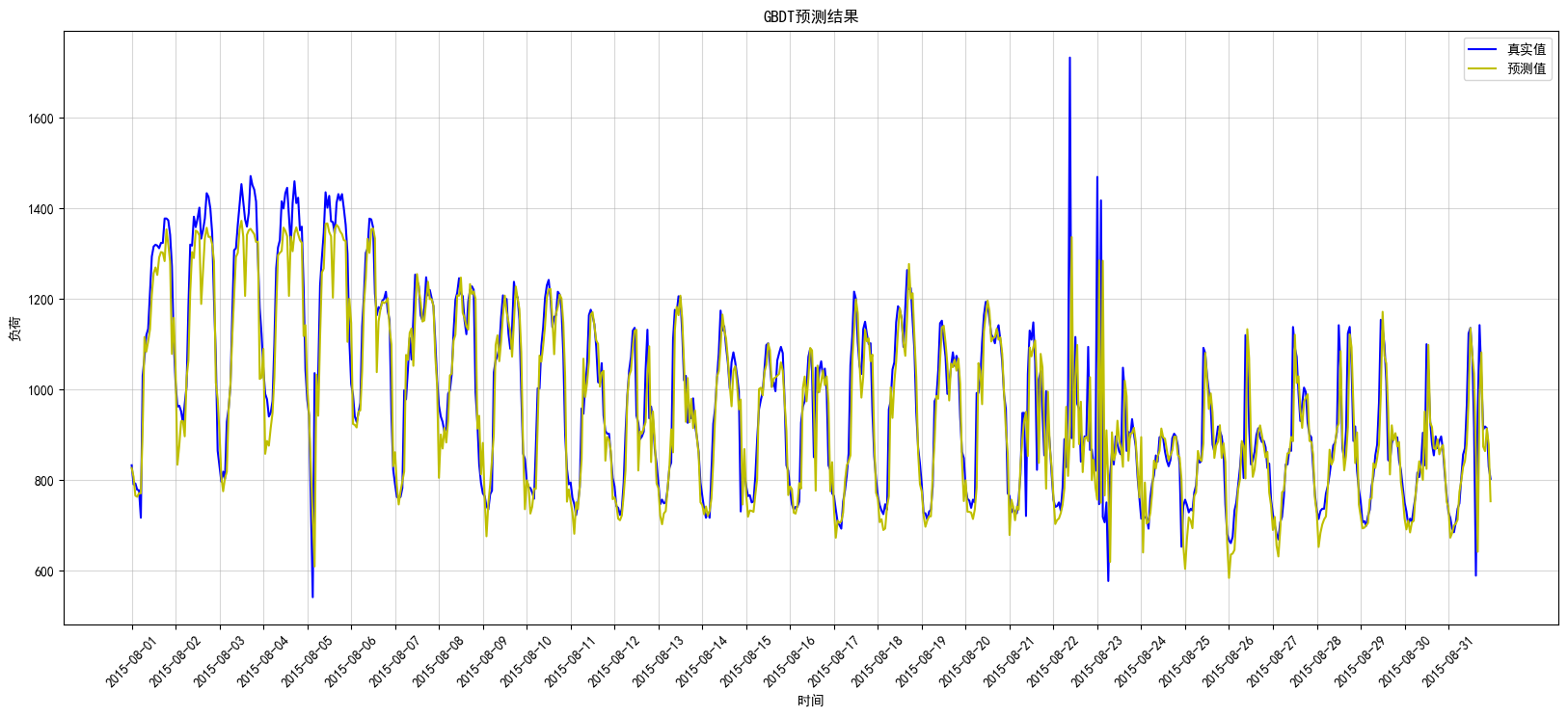
图7：GBDT测试图

从图中可以看出，GBDT对大部分数据拟合效果也较好，但除去可能的突变值之外，对于8月5号之前的数据拟合效果较之随机森林较差。

3.4.4 XGBoost

# 创建XGBoost模型对象.
estimator4 = xgb.XGBRegressor()

param_dict = {
    'max_depth': [1, 3, 5, 7, 9, 11],
    'n_estimators': [30, 50, 100, 150, 200, 250, 300],
    'learning_rate': [0.05, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0]
}
# 创建分层采样对象.
# 参1: 折数, 参2: 是否打乱(数据), 参3: 随机种子
kFold =KFold(n_splits=5, shuffle=True, random_state=64)
# 创建 网格搜索 + 交叉验证 对象.
gs_XGBoost = GridSearchCV(estimator4, param_dict,cv=kFold)

# 模型训练.
gs_XGBoost.fit(x_train, y_train)

# 模型预测.
y_pred4 = gs_XGBoost.predict(x_test)

# 模型评估.
print(f'XGBoost的MSE: {mean_squared_error(y_test, y_pred4)}')
print(f'XGBoost的RMSE: {np.sqrt(mean_squared_error(y_test, y_pred4))}')
print(f'XGBoost的MAE: {mean_absolute_error(y_test, y_pred4)}')
print(f'XGBoost的MAPE: {mean_absolute_percentage_error(y_test, y_pred4)}')
print(f'最佳参数为: {gs_XGBoost.best_params_}')

# 保存模型.
joblib.dump(estimator4, './model/XGBoost.pkl')

# 可视化XGBoost结果.
plt.figure(figsize=(20, 8), dpi=100)
plt.plot(df_test.time, y_test, color='b', label='真实值')
plt.plot(df_test.time, y_pred4, color='y', label='预测值')

# 创建网格.
plt.grid(True, alpha=0.5)
# 设置x轴显示格式.
plt.xticks(df_test.time[::24], rotation=45)

# 设置x轴, y轴, 标题
plt.xlabel('时间')
plt.ylabel('负荷')
plt.title('XGBoost预测结果')

# 显示图例
plt.legend()

# 显示图片
plt.show()

XGBoost在测试集上真实值与预测值的比对图见图8：

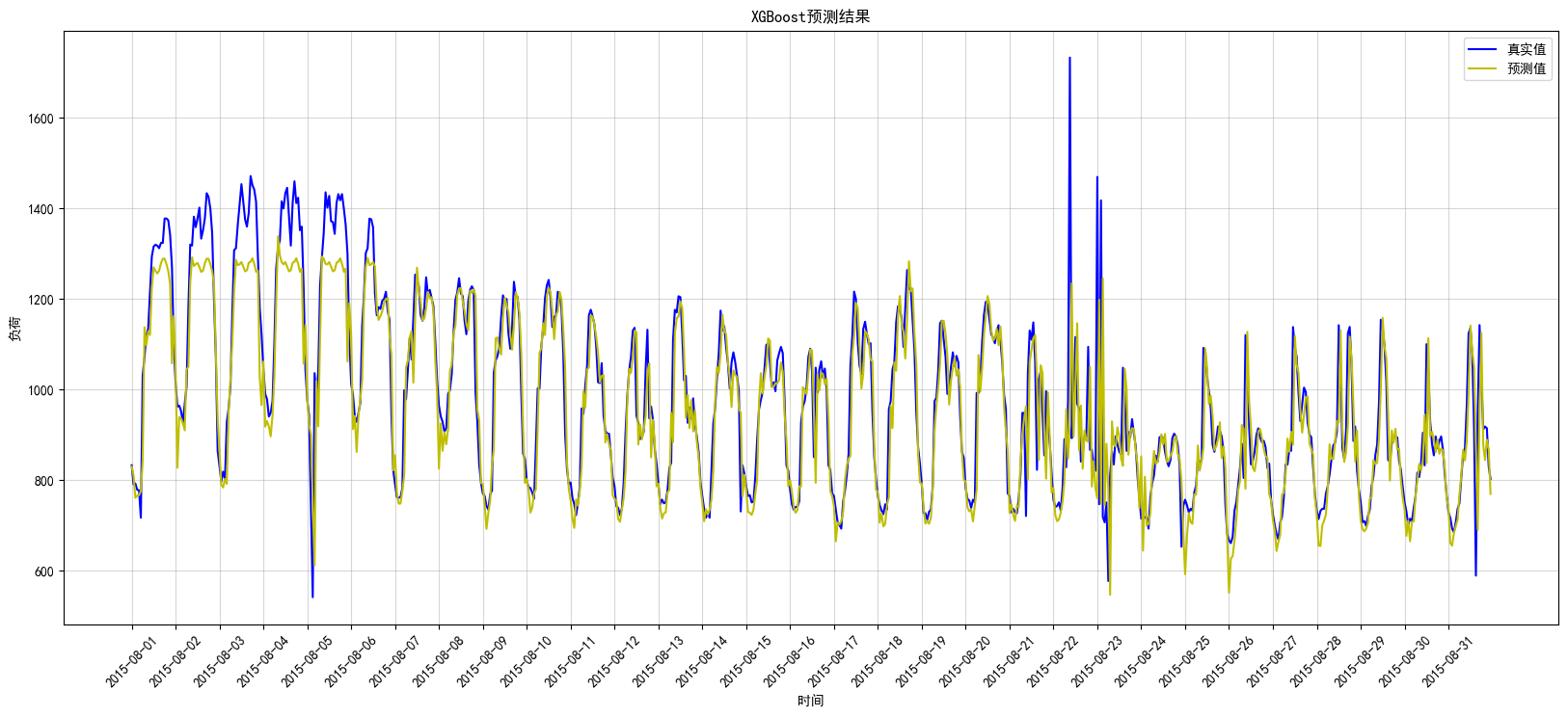
图8：XGBoost测试图

XGBoost同样拟合较好，除了异常值外，也出现了和GBDT的情况，即8月5日之前的数据拟合较差。

3.5 模型评估

各模型在测试集上的指标如下表：

表1：集成学习模型评估

|---------------|-------------|------------|-----------|----------|
| | MSE | RMSE | MAE | MAPE |
| Random_Forest | 9519.148092 | 97.566122 | 56.166173 | 0.056885 |
| AdaBoost | 10796.80613 | 103.907681 | 65.698295 | 0.065206 |
| GBDT | 8601.311736 | 92.743257 | 55.017936 | 0.056299 |
| XGBoost | 8891.217555 | 94.293253 | 57.498289 | 0.057488 |

从上表来看， 各性能表现最好的是GBDT，其次是XGBoost，最后是AdaBoost，但是这几者最坏的情况，误差范围亦不超过0.07，说明每个模型的拟合结果都较好。值得注意的是，虽然GBDT取得了较好的结果，但是由于其训练时间太长（1h43min），而XGBoost由于其可并行化，用时5min43s，因此综合考虑XGBoost会更好一些，另外两个模型训练时间均在16min左右。注意此处只是进行了简单地对比，由于模型会受到参数影响，并不能严格说明各自的性能差异。

4. 总结

从上述案例，我们可以看到机器学习的灵活性和对于复杂非线性数据的拟合优势，这是ARIMA模型所没有的，这在一定程度上改善了ARIMA模型对于时间序列要求平稳，以及灵活性较差的问题。在本专栏下一章节，将演示使用深度学习来进行时间序列分析，并说明其优势和缺点。