深度学习(Deep Learning, DL)是机器学习(Machine Learning, ML)的一个重要分支,核心是通过模拟人类大脑神经元的连接方式,构建多层神经网络来自动学习数据中的特征和规律,最终实现预测、分类、生成等任务。它摆脱了传统机器学习对 "人工设计特征" 的依赖,能直接从原始数据(如图像、文本、音频)中挖掘深层信息,是当前人工智能(AI)技术爆发的核心驱动力。
一、深度学习的核心思想:"多层" 与 "自动特征学习"
要理解深度学习,首先需要对比它与传统机器学习的核心差异:

举个直观例子:
- 用传统机器学习识别猫:需手动设计 "是否有胡须""是否有尖耳朵""毛色分布" 等特征,再喂给模型训练;
- 用深度学习识别猫:直接输入原始猫的图片,模型会自动从 "像素点→边缘→纹理→五官→完整猫轮廓" 逐层学习特征,无需人工干预。
二、深度学习的基础组件:神经网络的核心单元
深度学习的模型本质是多层神经网络,其最小组成单元和结构如下:
1. 基本单元:人工神经元(Artificial Neuron)
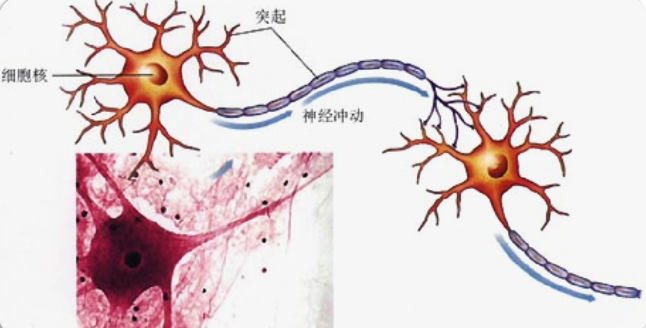
模拟生物神经元的 "接收信号→处理信号→输出信号" 过程,是神经网络的基础:
• 输入(Input):接收来自前一层的信号(如数据特征、前一层神经元的输出);
• 权重(Weight):每个输入对应一个权重(表示该输入的重要性,模型训练的核心就是优化权重);
• 偏置(Bias):调整神经元激活的 "基准线",避免仅由输入和权重决定输出;
• 激活函数(Activation Function):对 "输入 × 权重 + 偏置" 的结果进行非线性变换,让模型能学习复杂的非线性关系(如图像、语言中的复杂规律)。
常见激活函数:
- ReLU:最常用,公式
f(x) = max(0, x),解决 "梯度消失" 问题,计算高效; - Sigmoid:将输出压缩到 [0,1],适用于二分类任务的输出层;
- Tanh:将输出压缩到 [-1,1],比 Sigmoid 更对称,常用于早期模型的隐藏层。
- 这是生物上的神经元
- 这是计算机上的神经网络、
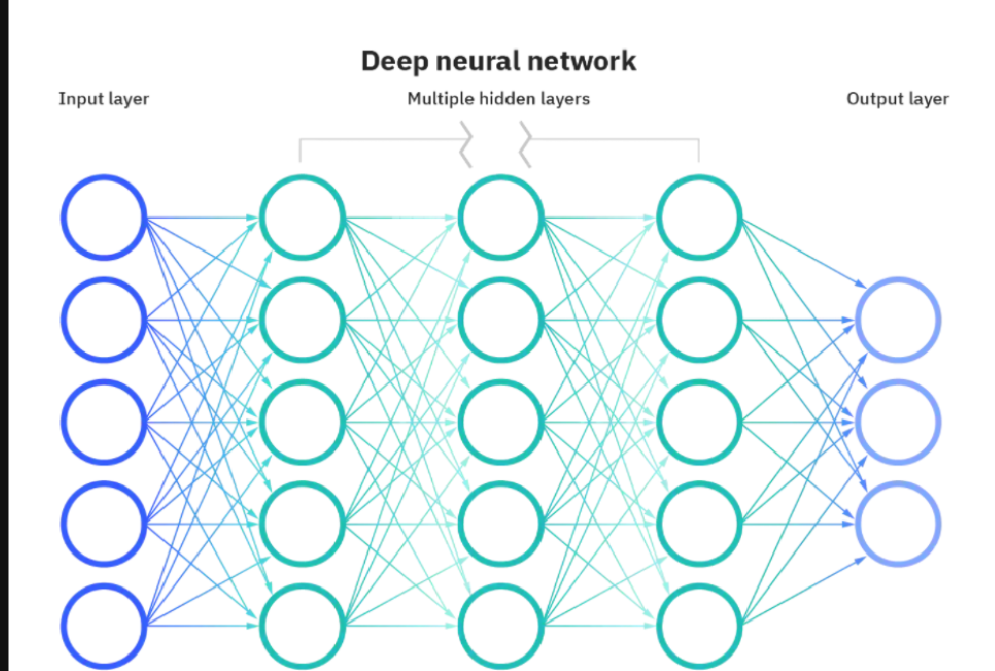
- 神经网络是由大量的节点(或称"神经元")和之间相互的联接构成。
- 每个节点代表一种特定的输出函数,称为激励函数、激活函数(activation function)。
- 每两个节点间的联接都代表一个对于通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。
2. 神经网络的层结构
多个人工神经元按 "层" 组织,形成神经网络,核心层包括:
• 输入层(Input Layer):接收原始数据(如图片的像素值、文本的向量),仅传递数据,不做计算;
• 隐藏层(Hidden Layer):对输入层的信号进行逐层加工、提取特征,"深度" 即指隐藏层的数量(通常≥2 层即可称为 "深度网络");
• 输出层(Output Layer):输出模型的最终结果,根据任务类型选择不同的激活函数:
◦ 分类任务:用 Softmax(多分类,输出各类别概率之和为 1);
◦ 回归任务:无激活函数(直接输出连续值);
◦ 二分类任务:用 Sigmoid(输出单个概率值)。
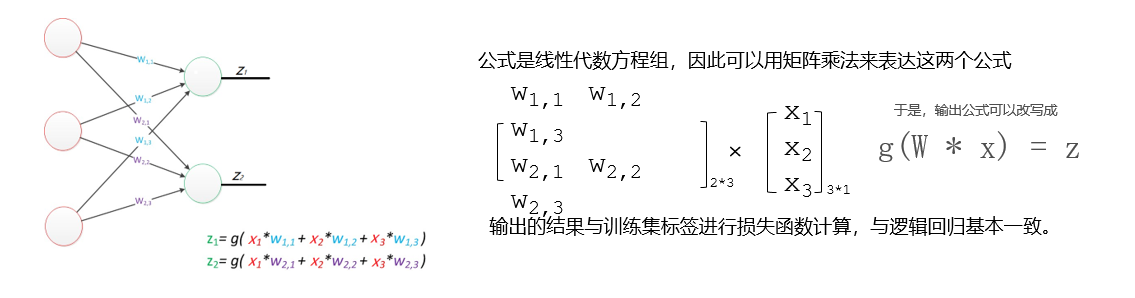
三、推导
- 以下是推导过程:
- 传入特征,按照不同的权重传入神经元进行求和
- 然后将结果放入sigmod函数进行非线性映射
- 最后得出分类结果

四、感知器与多层感知器
1.感知器
- 由两层神经元组成的神经网络--"感知器"(Perceptron),感知器只能线性划分数据。
- 因为只能通过一个线性函数(即加权和)将输入数据映射到输出类别
- 感知器图示
- 右下角是计算规则
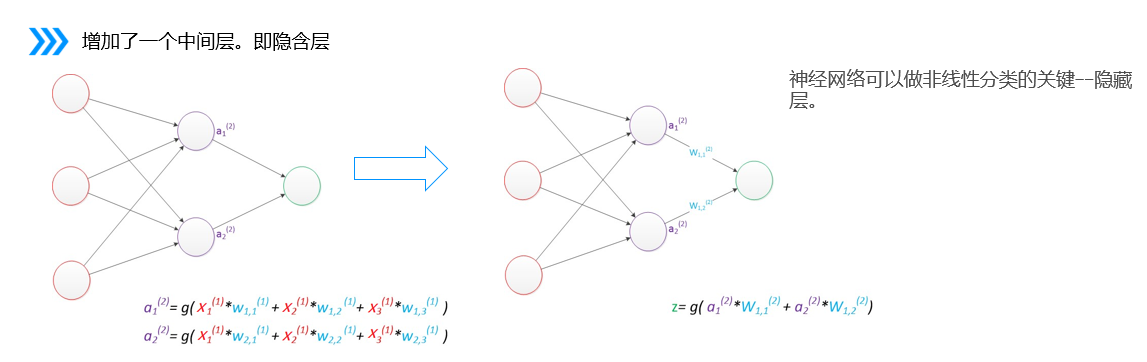
2.多层感知器
多层感知器(MLP)是深度学习中一种重要的神经网络结构,由多个层次的神经元组成,通常包括以下部分:
输入层:接收数据特征。
隐藏层:一个或多个,进行复杂的非线性变换。每层的神经元通过激活函数(如ReLU、Sigmoid)处理输入。
输出层:生成最终的预测结果或分类标签。
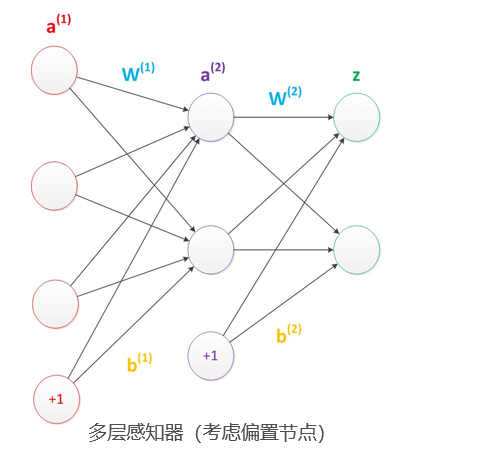
3.偏置
在神经网络中需要默认增加偏置神经元(节点),这些节点是默认存在的
它本质上是一个只含有存储功能,且存储值永远为1的单元
在神经网络的每个层次中,除了输出层以外,都会含有这样一个偏置单元
偏置节点没有输入(前一层中没有箭头指向它)
一般情况下,我们都不会明确画出偏置节点
调整决策边界:偏置项允许决策边界在特征空间中进行平移,而不仅仅是通过原点。
提高模型灵活性:使得神经网络能够捕捉到更多的数据模式和复杂性,即使在没有输入特征的情况下也能进行调整。
五、如何确定输入层和输出层个数
- 输入层的节点数:与特征的维度匹配
- 输出层的节点数:与目标的维度匹配。
- 中间层的节点数:目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值,通过切换这几个值来看整个模型的预测效果,选择效果最好的值作为最终选择。
六、损失函数
模型训练的目的:使得参数尽可能的与真实的模型逼近。
具体做法:
1、首先给所有参数赋上随机值。我们使用这些随机生成的参数值,来预测训练数据中的样本。
2、计算预测值为yi,真实值为y。那么,定义一个损失值loss,损失值用于判断预测的结果和真实值的误差,误差越小越好
常用的损失函数: 0-1损失函数 均方差损失 平均绝对差损失 交叉熵损失 合页损失
多分类的情况下,如何计算损失值
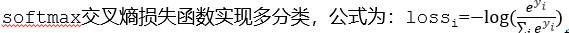
七、正则化惩罚
输入为[1,0,0,0]现有2种不同的权重值
w1 = [1,0,0,0]
w2 = [0.25,0.25,0.25,0.25]
w1和w2与输入的乘积都为1,但w2 与每一个输入数据进行计算后都有数据,使得w2会学习到每一个特征信息。而w1只和第1个输入信息有关系,容易出现过拟合现象,因此w2的效果会比w1 好
正则化惩罚的功能:主要用于惩罚权重参数w,一般有L1和L2正则化。
八、梯度下降
1. 偏导数
我们知道一个多变量函数的偏导数,就是它关于其中一个变量的导数而保持其他变量恒定。该函数的整个求导: 例如:计算像 f(b0,b1)=b0x1²* b1x2 这样的多变量函数的过程可以分解如下:

2. 梯度
梯度可以定义为一个函数的全部偏导数构成的向量,梯度向量的方向即为函数值增长最快的方向
3、梯度下降法
一个一阶最优化算法,通常也称为最陡下降法 ,要使用梯度下降法找到一个函数的局部极小值
步长(学习率):梯度可以确定移动的方向。学习率将决定我们采取步长的大小。不易过小和过大 如何解决全局最小的问题?产生多个随机数在不同的位置分别求最小值。
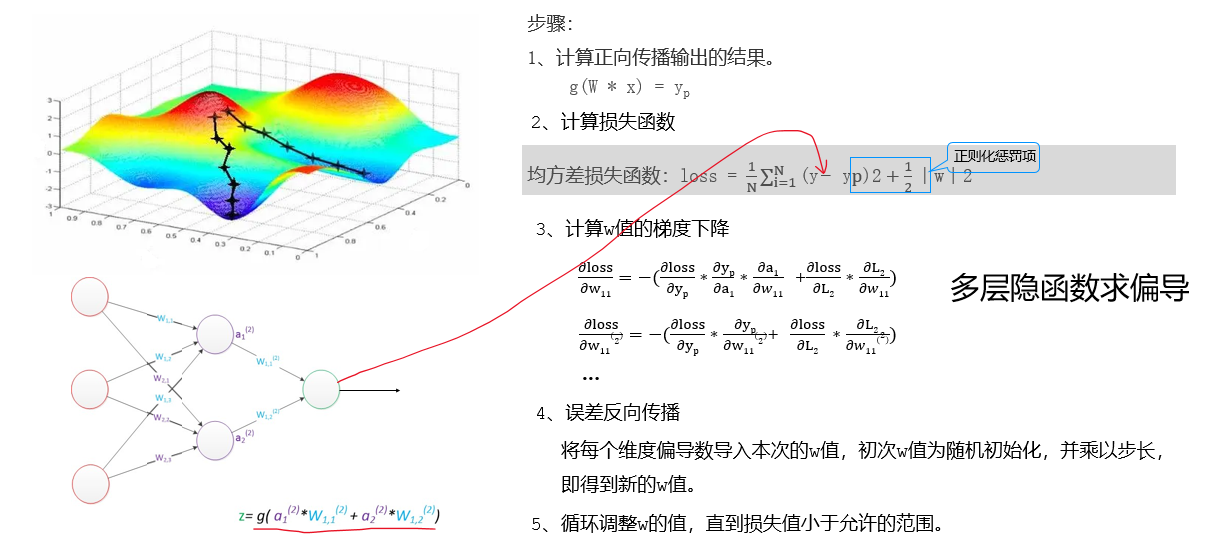
九、BP神经网络
BP(Back-propagation,反向传播)前向传播得到误差,反向传播调整误差,再前向传播,再反向传播一轮一轮得到最优解的。