【LeetCode】85. 最大矩形 (暴力枚举)

85. 最大矩形 - 力扣（LeetCode）

题目：

思路：

单调栈的运用

相似题：1504. 统计全 1 子矩形 - 力扣（LeetCode）

解法有两种，一种是暴力枚举，一种是单调栈优化

暴力做法很简单，我们同样枚举上界下界，然后枚举列数即可，同时这里我们可以使用一个简单的思路来计算连读h段的长度，可以先去写一下连续0段这题

代码很简单，但是时间复杂度很大，所以不妨考虑优化

我们发现我们题目其实可以变成一个柱形图，什么意思呢？

假设我们枚举到了第 i 行，那么对于每一个 sum[i][j]，我们定义为 i 位置往上的最长连读 1 的数量，那么这样一转换就变成了一个柱形图，如

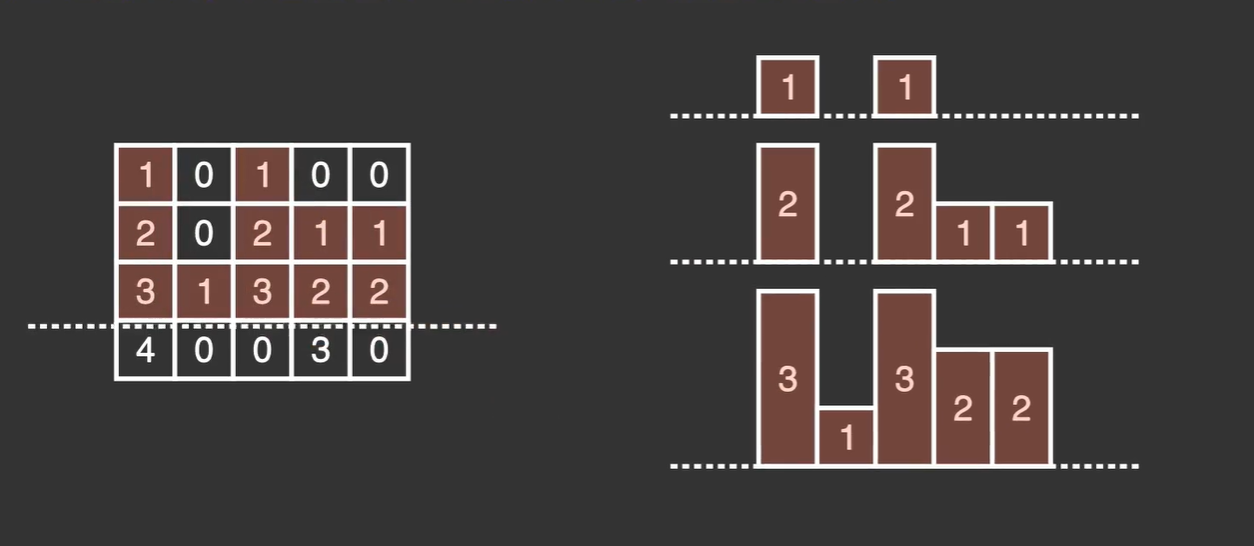
那么这样一直枚举行就相当于每次都求一个矩形图的最大矩形，这样以来我们就优化成了 O(N*M) 的复杂度，大大加快了速率

具体的，我们提前预处理出 sum[i][j]，然后暴力枚举 i，对每个 i 都做一个单调栈的操作，同时不要忘了哨兵

参考视频：LeetCode-85 最大矩形最近太忙啦！水一个视频～_哔哩哔哩_bilibili

代码：

cpp 复制代码

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int n = matrix.size();
        int m = matrix[0].size();
        int ans = 0;
        for(int i = 0;i < n;i++)
        {
            vector<int> sum(m,0);
            for(int j = i;j < n;j++)
            {
                int last = -1;
                int h = j - i + 1;
                for(int z =0;z < m;z++)
                {
                    sum[z] += matrix[j][z] - '0';
                    if(sum[z] == h) ans = max(ans,h * (z - last));
                    else last = z;
                }
            }
        }
        return ans;
    }
};

cpp 复制代码

class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int n = matrix.size();
        int m = matrix[0].size();
        vector<vector<int>> sum(n,vector<int>(m+2,0));
        for(int i = 0;i < n;i++)
        {
            for(int j = 0;j < m;j++)
            {
                if(matrix[i][j] == '0') 
                continue;
                if(i) 
                sum[i][j+1] = sum[i-1][j+1];
                sum[i][j+1]++;
            }
        }
        int ans = 0;
        for(int i = 0;i < n;i++)
        {
            stack<int> st;
            for(int j = 0;j < sum[i].size();j++)
            {
                while(!st.empty() && sum[i][st.top()] > sum[i][j])
                {
                    int h = sum[i][st.top()];
                    st.pop();
                    int w = j - st.top() - 1;
                    ans = max(ans,h*w);
                }
                st.push(j);
            }
        }
        return ans;
    }
};