目录
一、行列式
1.1二阶三阶行列式
1.2排列与逆序

1.3n阶行列式


1.4行列式的性质

1.5行列式按一行(列)展开

1.6行列式按多行展开


1.7行列式的计算


1.8克莱姆法则


二、矩阵
2.1矩阵的概念


2.2矩阵的加法、减法、数乘

2.3矩阵的乘法

2.4方阵的幂


2.5矩阵的转置

2.6方阵的行列式

2.7方阵的伴随矩阵


2.8逆矩阵




2.9矩阵的初等变换


2.10初等矩阵


2.11矩阵的等价

2.12初等行变换法求逆矩阵

2.13分块矩阵



2.14矩阵的秩



三、向量
3.1向量的概念与线性运算
3.2向量的线性组合与线性表示

3.3向量的线性相关性



3.4向量组的等价

3.5极大线性无关组


3.6向量组的秩

四、线性方程组
4.1线性方程组的表示法

4.2线性方程组解的判定


4.3线性方程组解的性质

4.4齐次线性方程组的基础解系


4.5方程组解的结构和求解


五、特征值与特征向量
5.1特征值和特征向量的定义

5.2特征值和特征向量的求法



5.3特征值和特征向量的性质


5.4相似矩阵的概念与性质


5.5矩阵的对角化

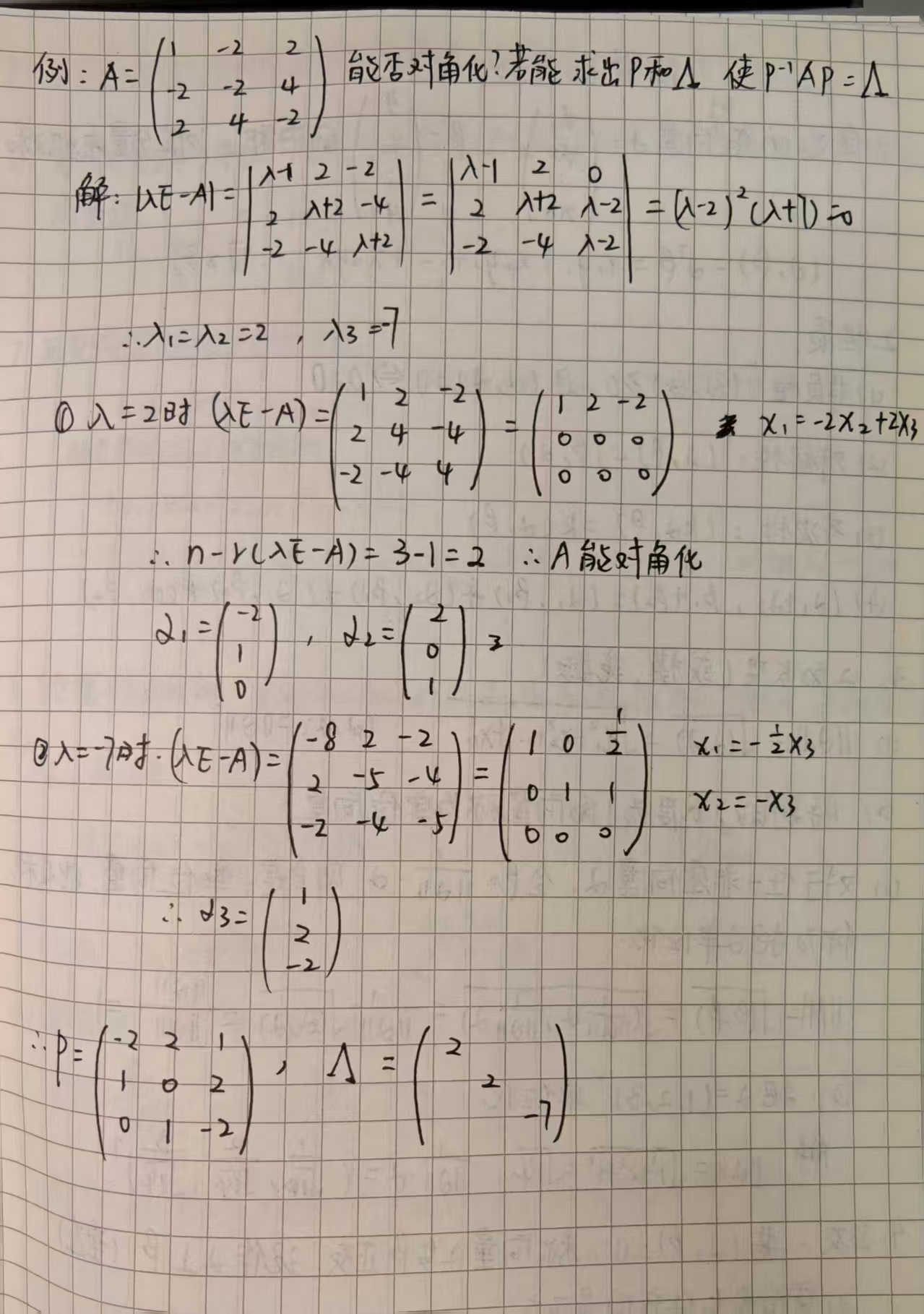
5.6内积与正交



5.7实对称矩阵的相似对角化

六、二次型
6.1二次型及矩阵表示




6.2化二次型为标准形


