注:
- 能力有限，敬请斧正
- 源码出自两个版本，因为有些特殊情况，笔者有空统一一下
Redis Scan 命令使用了一种独特的遍历算法------高位进位加法（Reverse Binary Iteration），这是一种巧妙的位运算技巧，确保了在哈希表扩容或缩容过程中能够安全、完整地遍历所有键值对，同时避免重复访问和遗漏。
Redis SCAN 为什么使用高位进位加法
1. 哈希表动态扩容的挑战
Redis 的哈希表会根据负载因子动态调整大小：
- 扩容：当负载因子过高时，哈希表大小翻倍
- 缩容：当负载因子过低时，哈希表大小减半
在传统遍历方式下，扩容或缩容会导致：
- 某些桶被重复访问
- 某些桶被遗漏
- 游标失效
2. 高位进位加法的优势
高位进位加法完美解决了这些问题：
优势一：扩容时的一致性当哈希表从大小
2^n 扩容到 2^(n+1) 时：
- 原来的桶
i会分裂成两个桶：i和i + 2^n - 高位进位加法确保这两个桶会在相邻的迭代中被访问
优势二：缩容时的安全性
当哈希表从大小 2^(n+1) 缩容到 2^n 时：
- 桶
i和i + 2^n会合并成一个桶i - 高位进位加法确保不会遗漏任何桶
优势三：游标的向前兼容性
无论哈希表如何变化，当前游标总是指向一个有效的位置，不会因为表大小变化而失效。
什么是高位进位加法
高位进位加法是一种特殊的二进制计数方式，与传统的低位进位不同，它从最高位开始进位。这种机制的核心思想是：在二进制表示中，从左到右（高位到低位）进行加法运算。
代码出自: github.com/redis/redis...
c
/* Redis 源码中的高位进位加法实现 */
static unsigned long rev(unsigned long v) {
/* bit size; must be power of 2 */
unsigned long s = CHAR_BIT * sizeof(v);
unsigned long mask = ~0UL;
while ((s >>= 1) > 0) {
mask ^= (mask << s);
v = ((v >> s) & mask) | ((v << s) & ~mask);
}
return v;
}
/* 注意⚠️：Redis8.0不存在该函数，我是把dictScanDefrag函数中相关内容摘出来了 */
unsigned long scan_cursor_next(unsigned long cursor, int bits) {
/* 将游标反转 */
cursor = rev(cursor, bits);
/* 加1 */
cursor++;
/* 再次反转得到下一个游标 */
return rev(cursor, bits);
}看不懂也没关系，我们转换为熟悉的知识，高位进位算法等效于下列操作：
- 将原数字所有位翻转(记做X)
- X+1(记做Y)
- 然后再将数字Y所有位翻转
如果还没理解，如表所示：假设我们有一个 4 位的哈希表（16 个桶），让我们看看高位进位加法的完整遍历序列：
yaml
步骤 游标(二进制) 游标(十进制) 反转后 +1后 再反转
1 0000 0 0000 0001 1000
2 1000 8 0001 0010 0100
3 0100 4 0010 0011 1100
4 1100 12 0011 0100 0010
5 0010 2 0100 0101 1010
6 1010 10 0101 0110 0110
7 0110 6 0110 0111 1110
8 1110 14 0111 1000 0001
9 0001 1 1000 1001 1001
10 1001 9 1001 1010 0101
11 0101 5 1010 1011 1101
12 1101 13 1011 1100 0011
13 0011 3 1100 1101 1011
14 1011 11 1101 1110 0111
15 0111 7 1110 1111 1111
16 1111 15 1111 10000 0000 (回到起点)高位进位怎么解决问题
举个例子：假设Hash的容量是8，那么Redis Scan的顺序是：
scss
0(000)
↓
4(100) ← 高位进位：0000 + 1 = 1000 (反转后)
↓
2(010) ← 高位进位：0100 + 1 = 1100 → 0010 (反转后)
↓
6(110)
↓
1(001)
↓
5(101)
↓
3(011)
↓
7(111)
↓
0(000) ← 回到起点1.考虑一个扩容的场景，扩容前容量为8，扩容后容量16
rust
原哈希表 (8个桶, 3位):
┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │
│000 │001 │010 │011 │100 │101 │110 │111 │
└─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘
扩容后 (16个桶, 4位):
┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │ 8 │ 9 │ 10 │ 11 │ 12 │ 13 │ 14 │ 15 │
│0000 │0001 │0010 │0011 │0100 │0101 │0110 │0111 │1000 │1001 │1010 │1011 │1100 │1101 │1110 │1111 │
└─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘
桶的分裂关系:
桶0(000) -> 桶0(0000) + 桶8(1000)
桶1(001) -> 桶1(0001) + 桶9(1001)
桶2(010) -> 桶2(0010) + 桶10(1010)
桶3(011) -> 桶3(0011) + 桶11(1011)
桶4(100) -> 桶4(0100) + 桶12(1100)
...如果SCAN每次只获取一个Buckt，执行SCAN 0 COUNT 1命令后会提示你下一次需要遍历的桶位是4；
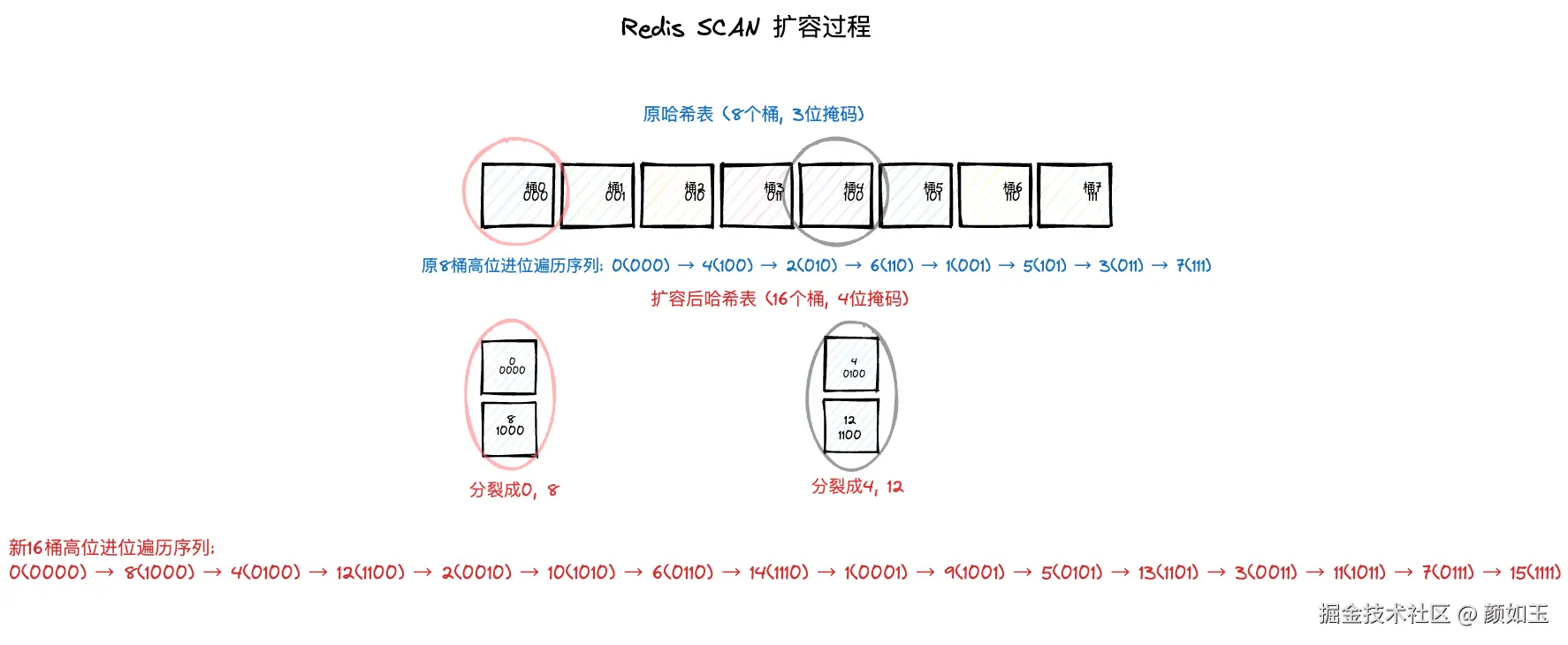在第一次,第二次SCAN之间，该Hash发生了一次扩容，那么我们可以注意到：
- 4依然是有效的桶位，
- 桶8直接会被跳过，因为之前的桶0被分裂为0，8，这样的话就不用重复遍历
- 剩下的(4,12)对应桶4，(2,10)对应桶2，(6，14)对应桶6，(1,9)对应桶1，(5,13)对应桶5，(3,11)对应桶3，(7,15)对应桶7，所有的桶也不会遗漏
2.考虑一个缩容的场景，缩容前容量为8，缩容后容量4
rust
原哈希表 (8个桶, 3位):
┌─────┬─────┬─────┬─────┬─────┬─────┬─────┬─────┐
│ 0 │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │
│000 │001 │010 │011 │100 │101 │110 │111 │
└─────┴─────┴─────┴─────┴─────┴─────┴─────┴─────┘
扩容后 (4个桶, 2位):
┌─────┬─────┬─────┬─────┐
│ 0 │ 1 │ 2 │ 3 │
│ 00 │ 01 │ 10 │ 11 │
└─────┴─────┴─────┴─────┘
桶的合并关系:
桶0(000) + 桶4(100) -> 桶0(00)
桶1(001) + 桶5(101) -> 桶1(01)
桶2(010) + 桶6(110) -> 桶2(10)
桶3(011) + 桶7(111) -> 桶3(11)
...同理如果SCAN每次只获取一个Buckt，执行SCAN 0 COUNT 1命令后会提示你下一次需要遍历的桶位是4。可是经过缩容之后仅仅只有0-3号桶，4号根本不存在，这样不是会有问题吗？显然缩容比扩容要麻烦一点
c
unsigned long dictScan(dict *d, unsigned long v, dictScanFunction *fn, void *privdata) {
dictht *t0, *t1;
const dictEntry *de;
unsigned long m0, m1;
/* 跳过空字典 */
if (dictSize(d) == 0) return 0;
/* 迭代只有一个哈希表的字典，查看字典是否正在 rehash */
if (!dictIsRehashing(d)) {
/* 这里直接省略 */
} else {
/* 迭代有两个哈希表的字典；指向两个哈希表 */
t0 = &d->ht[0];
t1 = &d->ht[1];
/* Make sure t0 is the smaller and t1 is the bigger table；确保 t0 比 t1 要小 */
if (t0->size > t1->size) {
t0 = &d->ht[1];
t1 = &d->ht[0];
}
/* 记录掩码 */
m0 = t0->sizemask;//11
m1 = t1->sizemask;//111
/* Emit entries at cursor；指向桶，并迭代桶中的所有节点*/
de = t0->table[v & m0];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Iterate over indices in larger table that are the expansion
* of the index pointed to by the cursor in the smaller table
* Iterate over indices in larger table 迭代大表中的桶
* that are the expansion of the index pointed to 这些桶被索引的 expansion 所指向
* by the cursor in the smaller table
*/
do {
/* Emit entries at cursor 指向桶，并迭代桶中的所有节点 */
de = t1->table[v & m1];
while (de) {
fn(privdata, de);
de = de->next;
}
/* Increment bits not covered by the smaller mask */
v = (((v | m0) + 1) & ~m0) | (v & m0);
/* Continue while bits covered by mask difference is non-zero */
} while (v & (m0 ^ m1));
}
}这段代码大致意思是:
首先交换两个掩码，永远保证m0 < m1，结合例子就是m0 = 11，m1 = 111，同时交换过t0，t1结合本例前者表示缩容之后的Hash，后者表示原Hash； t0->table[v & m0]的含义是就是新Hash的[11 & 100]0号桶。
紧接着，do-while 循环开始扫描旧表(大表t1)中"相关的桶"。目的就是寻找那些还未被迁移、仍然留在旧家(大表)的元素。
"相关的桶"是指在缩容时，大表中的多个桶会被合并到小表的一个桶里。例如，从size=8缩到size=4，旧表（大表）中的桶0和桶4的元素，都会被迁移到新表(小表)的桶0中。
最后返回2，表示下次扫描2号桶。
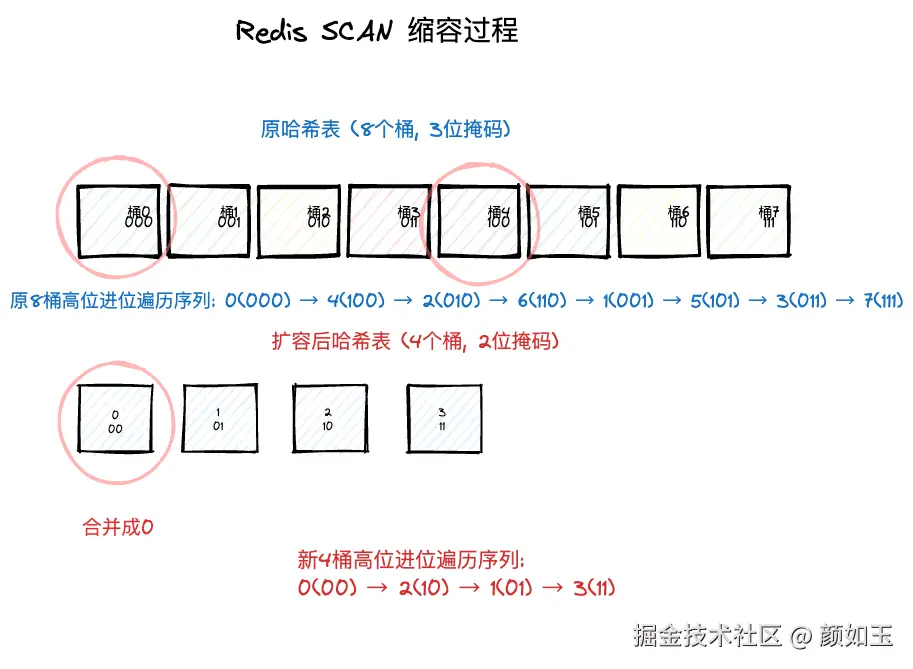假如是在第二次,第三次SCAN之间，该Hash发生了一次缩容，那么更加简单，我们可以注意到：
- 2依然是有效的桶位，
- 旧Hash的0，4号桶已经遍历完毕，直接跳过
- 剩下的(2,6)对应桶2，(1,5)对应桶1，(3，7)对应桶3，所有的桶也不会遗漏
Redis SCAN 的高位进位加法机制是一个精妙的算法设计，它完美解决了在动态哈希表中进行安全遍历的难题(但是可能会重复，对扫描过的桶中新加入的元素也会遗漏)。