题⽬描述
输⼊⼀颗⼆叉树的根节点和⼀个整数,按字典序打印出⼆叉树中结点值的和为输⼊整数的所有路径。路径定义为从树的根结点开始往下⼀直到叶结点所经过的结点形成⼀条路径。
- 该题路径定义为从树的根结点开始往下⼀直到叶⼦结点所经过的结点
- 叶⼦节点是指没有⼦节点的节点
- 路径只能从⽗节点到⼦节点,不能从⼦节点到⽗节点
- 总节点数⽬为 n
例如:给出如下二叉树,sum=22
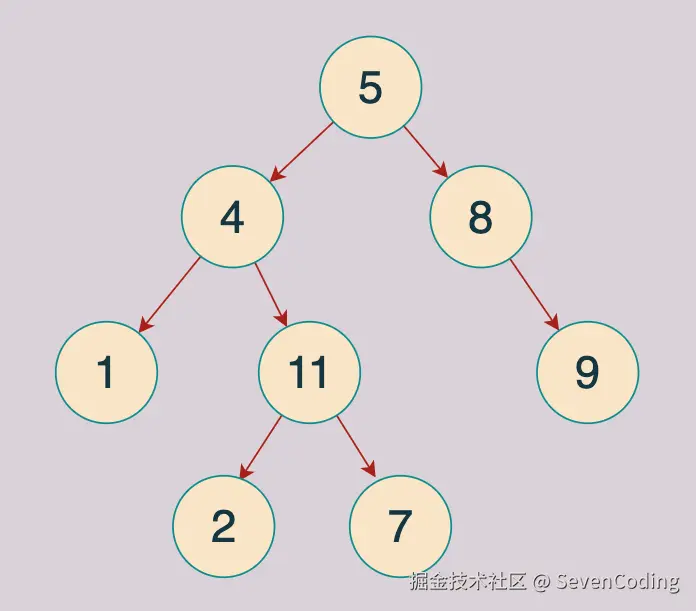
返回true ,因为存在⼀条路径 5 -> 4 -> 11 -> 2 的节点值之和为 22
思路及解答
递归回溯法(推荐)
递归回溯法是解决这类问题的经典方法:
- 前序遍历:从根节点开始,先访问当前节点,再递归访问左右子节点
- 路径记录:使用一个列表记录当前路径上的节点值
- 目标值递减:每次递归时将目标值减去当前节点值
- 叶子节点检查:到达叶子节点时检查剩余目标值是否为0
- 回溯处理:在递归返回前需要移除当前节点,以便尝试其他路径
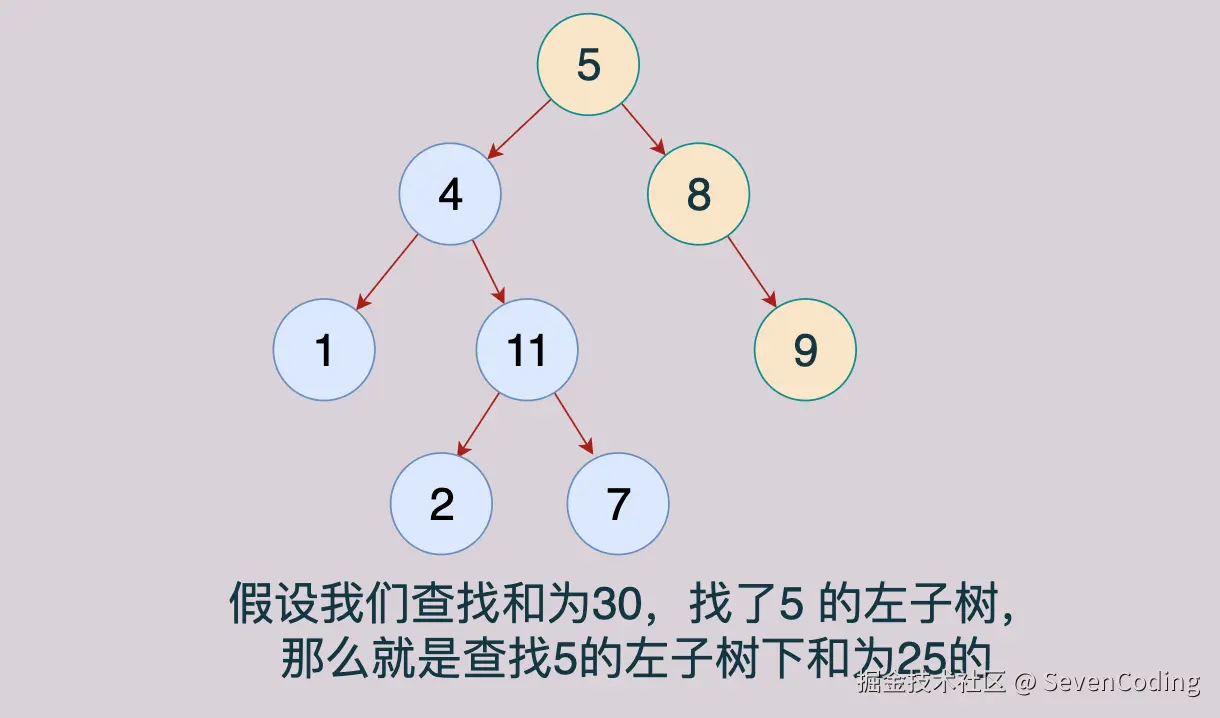
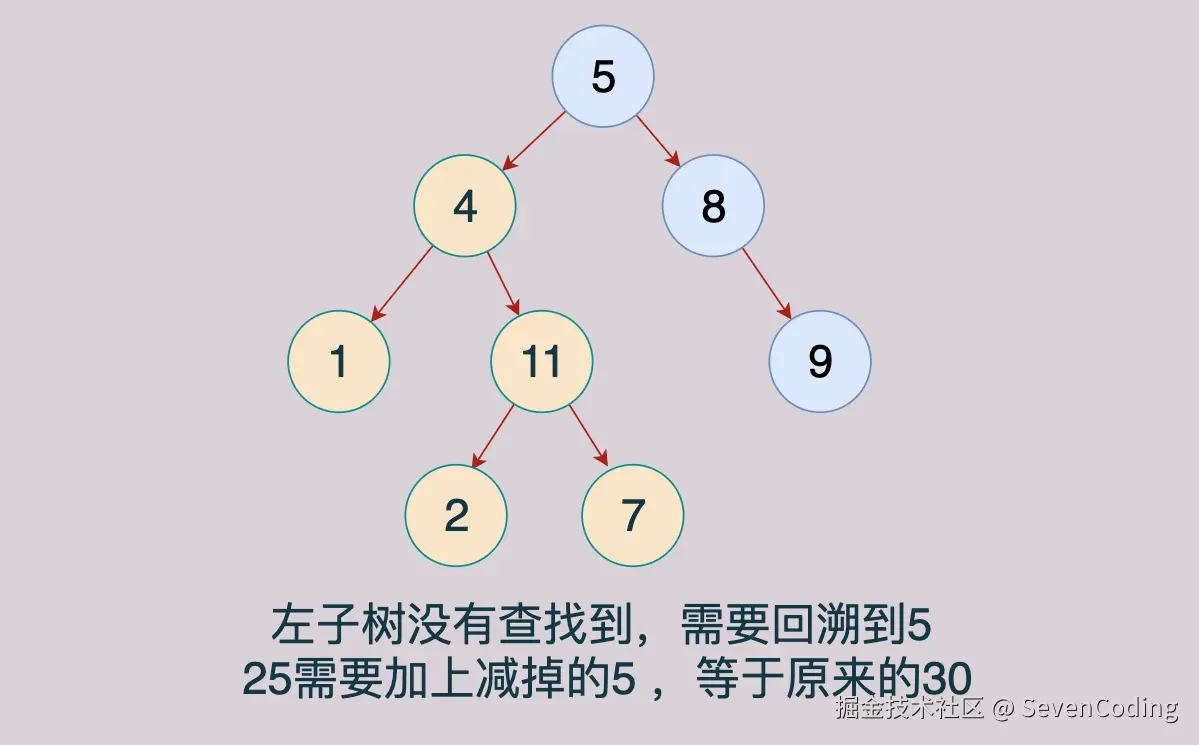
java
public class Solution {
// 存储所有符合条件的路径
List<List<Integer>> result = new ArrayList<>();
// 存储当前路径
List<Integer> path = new ArrayList<>();
public List<List<Integer>> FindPath(TreeNode root, int targetSum) {
if (root == null) {
return result;
}
dfs(root, targetSum);
return result;
}
private void dfs(TreeNode node, int remainingSum) {
if (node == null) {
return;
}
// 将当前节点加入路径
path.add(node.val);
remainingSum -= node.val;
// 检查是否为叶子节点且路径和等于目标值
if (node.left == null && node.right == null && remainingSum == 0) {
result.add(new ArrayList<>(path)); // 必须新建一个ArrayList
}
// 递归处理左右子树
dfs(node.left, remainingSum);
dfs(node.right, remainingSum);
// 回溯,移除当前节点
path.remove(path.size() - 1);
}
}- 时间复杂度:O(n),n 为⼆叉树的节点个数,遍历完所有的节点
- 空间复杂度:O(n),借助了额外的空间
迭代法(使用栈模拟递归)
使用栈来模拟递归过程,避免递归带来的栈溢出风险:
- 双栈结构:一个栈存储节点,一个栈存储剩余目标值
- 路径记录:使用链表记录当前路径,方便回溯
- 后进先出:按照前序遍历的顺序处理节点
java
public class Solution {
public List<List<Integer>> FindPath(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Deque<TreeNode> nodeStack = new LinkedList<>();
Deque<Integer> sumStack = new LinkedList<>();
Deque<List<Integer>> pathStack = new LinkedList<>();
nodeStack.push(root);
sumStack.push(targetSum);
pathStack.push(new ArrayList<>(Arrays.asList(root.val)));
while (!nodeStack.isEmpty()) {
TreeNode node = nodeStack.pop();
int remainingSum = sumStack.pop();
List<Integer> currentPath = pathStack.pop();
// 检查是否为叶子节点且路径和等于目标值
if (node.left == null && node.right == null && remainingSum == node.val) {
result.add(new ArrayList<>(currentPath));
}
// 右子节点先入栈,保证左子节点先处理
if (node.right != null) {
nodeStack.push(node.right);
sumStack.push(remainingSum - node.val);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(node.right.val);
pathStack.push(newPath);
}
if (node.left != null) {
nodeStack.push(node.left);
sumStack.push(remainingSum - node.val);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(node.left.val);
pathStack.push(newPath);
}
}
return result;
}
}- 时间复杂度:O(n)
- 空间复杂度:O(n),需要存储节点和路径信息
BFS层序遍历
使用队列进行广度优先搜索,同时记录路径和:
- 节点队列:存储待处理的节点
- 路径队列:存储从根节点到当前节点的路径
- 和队列:存储从根节点到当前节点的路径和
java
public class Solution {
public List<List<Integer>> FindPath(TreeNode root, int targetSum) {
List<List<Integer>> result = new ArrayList<>();
if (root == null) {
return result;
}
Queue<TreeNode> nodeQueue = new LinkedList<>();
Queue<List<Integer>> pathQueue = new LinkedList<>();
Queue<Integer> sumQueue = new LinkedList<>();
nodeQueue.offer(root);
pathQueue.offer(new ArrayList<>(Arrays.asList(root.val)));
sumQueue.offer(root.val);
while (!nodeQueue.isEmpty()) {
TreeNode node = nodeQueue.poll();
List<Integer> currentPath = pathQueue.poll();
int currentSum = sumQueue.poll();
// 检查是否为叶子节点且路径和等于目标值
if (node.left == null && node.right == null && currentSum == targetSum) {
result.add(new ArrayList<>(currentPath));
}
if (node.left != null) {
nodeQueue.offer(node.left);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(node.left.val);
pathQueue.offer(newPath);
sumQueue.offer(currentSum + node.left.val);
}
if (node.right != null) {
nodeQueue.offer(node.right);
List<Integer> newPath = new ArrayList<>(currentPath);
newPath.add(node.right.val);
pathQueue.offer(newPath);
sumQueue.offer(currentSum + node.right.val);
}
}
return result;
}
}- 时间复杂度:O(n)
- 空间复杂度:O(n),队列存储节点的空间