2025-08-26：最长 V 形对角线段的长度。用go语言，给定一个 n × m 的整型矩阵，每个格子的值为 0、1 或 2。需要找出一种沿对角方向移动的连续

2025-08-26：最长 V 形对角线段的长度。用go语言，给定一个 n × m 的整型矩阵，每个格子的值为 0、1 或 2。需要找出一种沿对角方向移动的连续格子路径，其规则如下：

路径的第一个格子必须为 1；
之后每一步沿某一对角方向前进（四个对角方向之一），且相邻格子必须紧邻（不能跳格）；
格子的值从第 2 个开始按 2、0、2、0... 交替出现（即第一个是 1，第二个必须是 2，第三个是 0，以此类推）；
在整个路径中，允许最多在某一位置改变一次移动方向，并且该改变必须是向右旋转 90 度（即改变为另一个对角方向）；转向前后都必须继续满足值的交替要求。

要求返回满足上述条件的路径的最大长度（格子数量）。如果不存在任何符合条件的路径，则返回 0。

n == grid.length。

m == grid[i].length。

1 <= n, m <= 500。

grid[i][j] 的值为 0、1 或 2。

输入： grid = [[2,2,1,2,2],[2,0,2,2,0],[2,0,1,1,0],[1,0,2,2,2],[2,0,0,2,2]]。

输出： 5。

解释：

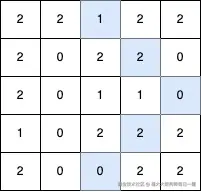
最长的 V 形对角线段长度为 5，路径如下：(0,2) → (1,3) → (2,4)，在 (2,4) 处进行顺时针 90 度转向，继续路径为 (3,3) → (4,2)。

题目来自力扣3459。

分步骤描述过程

问题分析 ：

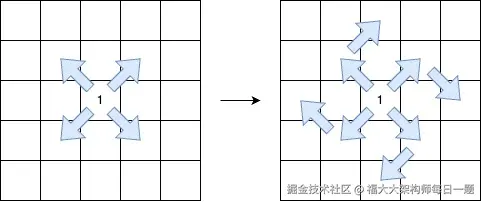
我们需要在网格中寻找最长的V形对角路径。路径起始于值为1的格子，后续格子值必须交替为2和0（即1之后是2，然后是0，再是2，以此类推）。路径沿四个对角方向（东北、西北、西南、东南）移动，且最多允许一次90度转向（顺时针或逆时针？但题目要求是向右旋转90度，即顺时针）。路径必须是连续的（相邻格子）。
记忆化DFS（动态规划）设置：
- 定义四个对角方向的方向向量：dirs = [4][2]int{{1,1}, {1,-1}, {-1,-1}, {-1,1}}，分别对应东南、西南、西北、东北。
- 创建一个四维记忆数组memo，维度为[m][n][4][2]。其中：
  - memo[i][j][d][t]表示从位置(i,j)出发，当前方向为d（0到3），且是否已经使用过转向（t=0表示未使用，t=1表示已使用）时，能获得的最大路径长度（包括当前格子）。
- 初始化memo所有值为-1，表示未计算。
DFS函数设计：
- 函数签名：dfs(cx, cy, direction int, turn bool, target int) int
  - (cx,cy)：当前格子坐标。
  - direction：当前移动方向（0到3）。
  - turn：布尔值，表示是否已经使用过转向（true表示还可以转向，false表示已使用过？但注意：在调用中，初始时turn=true表示允许转向，而递归时若已转向则传入false）。
  - target：下一个格子期望的值（根据交替规则：当前格子是1则下一个应为2；当前是2则下一个应为0；当前是0则下一个应为2）。
- 步骤： a. 计算下一个格子坐标(nx, ny)。 b. 检查边界：如果(nx,ny)越界或值不等于target，返回0（无法继续）。 c. 检查记忆数组：如果已计算过，直接返回结果。 d. 递归计算： - 不转向：继续沿原方向移动，递归调用dfs(nx, ny, direction, turn, next_target)（其中next_target为2-target，因为0和2交替）。 - 如果允许转向（turn==true），则尝试顺时针旋转90度（即方向变为(direction+1)%4），并递归调用（传入turn=false表示已使用转向）。 e. 取两种选择的最大值，加1（当前格子）后存入记忆数组并返回。
主循环：
- 遍历每个格子(i,j)，如果值为1，则作为路径起点。
- 对于每个起点，尝试四个初始方向，调用dfs(i, j, direction, true, 2)（因为起点是1，下一个期望值是2）。
- 取所有结果的最大值（并加1，因为起点本身也算），作为最终答案。
示例路径验证 ：

对于示例网格，路径(0,2)→(1,3)→(2,4)→(3,3)→(4,2)： - (0,2)=1（起点）。 - (1,3)=2（符合期望）。 - (2,4)=0（符合期望）。 - 在(2,4)处转向（顺时针90度：原方向是东南[1,1]？但实际从(1,3)到(2,4)是东南，转向后应为西南[1,-1]？但西南方向到(3,3)是合理的）。 - (3,3)=2（符合期望）。 - (4,2)=0（符合期望）。路径长度为5。
终止条件：
- 当下一步越界或值不满足期望时，返回0。
- 记忆化避免重复计算。

时间复杂度和额外空间复杂度

时间复杂度 ：

每个状态由(i, j, direction, turn)定义，共有m * n * 4 * 2 = 8*m*n个状态。每个状态计算时最多进行两次递归调用（不转向和转向），但实际由于记忆化，每个状态只计算一次。因此总时间复杂度为O(m*n)（因为常数因子8，但通常忽略），即与网格大小成线性。
额外空间复杂度 ：

记忆数组memo大小为m * n * 4 * 2，即8mn 。递归深度最多为路径长度（但路径长度不会超过max(m,n)，因此递归栈空间可忽略）。总额外空间为O(m*n)。

总结：该算法通过记忆化DFS有效避免了重复计算，在网格问题上实现了线性时间复杂度和线性空间复杂度。

Go完整代码如下：

go 复制代码

package main

import (
	"fmt"
)

func lenOfVDiagonal(grid [][]int) int {
	dirs := [4][2]int{{1, 1}, {1, -1}, {-1, -1}, {-1, 1}}
	m, n := len(grid), len(grid[0])
	memo := make([][][4][2]int, m)
	for i := range memo {
		memo[i] = make([][4][2]int, n)
		for j := range memo[i] {
			for k := range memo[i][j] {
				for l := range memo[i][j][k] {
					memo[i][j][k][l] = -1
				}
			}
		}
	}

	var dfs func(cx, cy, direction int, turn bool, target int) int
	dfs = func(cx, cy, direction int, turn bool, target int) int {
		nx, ny := cx+dirs[direction][0], cy+dirs[direction][1]
		/* 如果超出边界或者下一个节点值不是目标值，则返回 */
		if nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] != target {
			return 0
		}

		turnInt := 0
		if turn {
			turnInt = 1
		}
		if memo[nx][ny][direction][turnInt] != -1 {
			return memo[nx][ny][direction][turnInt]
		}

		/* 按照原来的方向继续行走 */
		maxStep := dfs(nx, ny, direction, turn, 2-target)
		if turn {
			/* 顺时针旋转 90 度转向 */
			maxStep = max(maxStep, dfs(nx, ny, (direction+1)%4, false, 2-target))
		}
		memo[nx][ny][direction][turnInt] = maxStep + 1
		return maxStep + 1
	}

	res := 0
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			if grid[i][j] == 1 {
				for direction := 0; direction < 4; direction++ {
					res = max(res, dfs(i, j, direction, true, 2)+1)
				}
			}
		}
	}
	return res
}

func main() {
	grid := [][]int{{2, 2, 1, 2, 2}, {2, 0, 2, 2, 0}, {2, 0, 1, 1, 0}, {1, 0, 2, 2, 2}, {2, 0, 0, 2, 2}}
	result := lenOfVDiagonal(grid)
	fmt.Println(result)
}

Python完整代码如下：

python 复制代码

# -*-coding:utf-8-*-

import sys

sys.setrecursionlimit(10**6)

def lenOfVDiagonal(grid):
    if not grid or not grid[0]:
        return 0

    m, n = len(grid), len(grid[0])
    dirs = [(1, 1), (1, -1), (-1, -1), (-1, 1)]
    # memo[x][y][direction][turnInt]，turnInt: 1 表示还可以转，0 表示已经转过
    memo = [[[[ -1 for _ in range(2)] for _ in range(4)] for _ in range(n)] for _ in range(m)]

    def dfs(cx, cy, direction, turn, target):
        nx = cx + dirs[direction][0]
        ny = cy + dirs[direction][1]
        # 越界或值不符合目标
        if nx < 0 or ny < 0 or nx >= m or ny >= n or grid[nx][ny] != target:
            return 0

        turnInt = 1 if turn else 0
        if memo[nx][ny][direction][turnInt] != -1:
            return memo[nx][ny][direction][turnInt]

        # 继续沿原方向走
        maxStep = dfs(nx, ny, direction, turn, 2 - target)
        # 如果还可以转，则尝试顺时针转 90 度（direction+1）
        if turn:
            maxStep = max(maxStep, dfs(nx, ny, (direction + 1) % 4, False, 2 - target))

        memo[nx][ny][direction][turnInt] = maxStep + 1
        return memo[nx][ny][direction][turnInt]

    res = 0
    for i in range(m):
        for j in range(n):
            if grid[i][j] == 1:
                for direction in range(4):
                    # dfs 从下一个格子开始计数，+1 把起点的 1 也算上
                    res = max(res, dfs(i, j, direction, True, 2) + 1)
    return res

if __name__ == "__main__":
    grid = [
        [2, 2, 1, 2, 2],
        [2, 0, 2, 2, 0],
        [2, 0, 1, 1, 0],
        [1, 0, 2, 2, 2],
        [2, 0, 0, 2, 2],
    ]
    print(lenOfVDiagonal(grid))