用 PyTorch 从零实现 MNIST 手写数字识别

dlraba8022025-08-27 20:22

在深度学习入门阶段，MNIST 手写数字识别是经典的 "Hello World" 项目。它不仅能帮助我们熟悉深度学习的核心流程，还能直观理解神经网络如何从数据中学习规律。本文将基于 PyTorch 框架，从零拆解 MNIST 识别模型的实现过程，涵盖数据准备、模型构建、训练优化到性能评估的全流程，并深入讲解每一步背后的原理。

一、环境准备与核心库导入

在开始前，需确保已安装 PyTorch 环境（建议搭配torchvision用于加载数据集）。首先导入所需库，这是构建深度学习模型的基础。

python 复制代码 
# 导入PyTorch核心库并验证版本
import torch
print(torch.__version__)  # 打印版本号，确保环境配置正确（本文基于2.0+版本测试）

# 导入神经网络与数据处理相关模块
from torch import nn  # 神经网络核心层（如Linear、Flatten）
from torch.utils.data import DataLoader  # 数据批量加载工具
from torchvision import datasets  # 计算机视觉常用数据集（含MNIST）
from torchvision.transforms import ToTensor  # 图像格式转换工具

核心库作用解析

  • torch：PyTorch 的主库，提供张量计算、自动微分等核心功能，是所有操作的基础。
  • torch.nn：封装了神经网络的常用组件（如全连接层、激活函数、损失函数），简化模型定义流程。
  • torch.utils.data.DataLoader：将数据集按批次拆分，支持多线程加载，是高效训练的关键工具。
  • torchvision.datasets：提供经典视觉数据集（如 MNIST、CIFAR），支持自动下载，无需手动处理数据文件。
  • torchvision.transforms.ToTensor ：将图像从 PIL 格式（或 numpy 数组）转换为 PyTorch 的Tensor格式，并将像素值从0-255归一化到0-1，符合神经网络的输入要求。

二、数据加载与预处理

深度学习的效果依赖高质量数据，MNIST 数据集是手写数字识别的标准数据集，包含 60000 张训练图像和 10000 张测试图像，每张图像为 28×28 像素的灰度图，标签对应 0-9 的数字类别。

1. 加载 MNIST 数据集

python 复制代码 
# 加载训练集
training_data = datasets.MNIST(
    root='data',  # 数据存储路径（本地不存在时自动创建）
    train=True,   # True表示加载训练集，False表示加载测试集
    download=True,  # 本地无数据时自动从官网下载（约10MB）
    transform=ToTensor(),  # 数据转换：PIL→Tensor+归一化
)

# 加载测试集
test_data = datasets.MNIST(
    root='data',
    train=False,  # 加载测试集（用于评估模型泛化能力）
    download=True,
    transform=ToTensor(),
)

# 验证数据加载效果：打印训练集样本数量
print(f"训练集样本数：{len(training_data)}")  # 输出：60000
print(f"测试集样本数：{len(test_data)}")      # 输出：10000

2. 创建 DataLoader：批量加载数据

直接遍历原始数据集效率低，DataLoader可将数据按批次（batch_size）拆分，同时支持随机打乱（shuffle=True）和多线程加载，大幅提升训练效率。

python 复制代码 
# 训练集DataLoader：batch_size=64（每次处理64张图像）
train_dataloader = DataLoader(training_data, batch_size=64, shuffle=True)
# 测试集DataLoader：无需打乱（评估时只需按序计算）
test_dataloader = DataLoader(test_data, batch_size=64, shuffle=False)

# 验证DataLoader输出格式
for X, y in test_dataloader:
    print(f"输入图像X的形状：[N, C, H, W] = {X.shape}")  # 输出：[64, 1, 28, 28]
    print(f"标签y的形状：[N] = {y.shape}")              # 输出：[64]
    print(f"标签y的数据类型：{y.dtype}")                # 输出：torch.int64
    break
维度含义解析
  • X.shape = [64, 1, 28, 28] ：N=64（批次大小）、C=1（通道数，灰度图为 1，彩色图为 3）、H=28（图像高度）、W=28（图像宽度）。
  • y.shape = [64]：每个样本对应 1 个标签（0-9 的整数），与批次大小一致。

三、选择计算设备（CPU/GPU）

神经网络训练依赖大量矩阵运算，GPU（尤其是 NVIDIA GPU）能大幅加速计算。PyTorch 支持自动检测并选择最优设备，代码如下：

python 复制代码 
# 优先级：NVIDIA GPU (cuda) → Apple M系列GPU (mps) → CPU
device = (
    "cuda"
    if torch.cuda.is_available()
    else "mps"
    if torch.backends.mps.is_available()
    else "cpu"
)
print(f"使用计算设备：{device}")
  • cuda：适用于 NVIDIA 显卡（需安装 CUDA Toolkit），训练速度比 CPU 快 10-100 倍。
  • mps：适用于 Apple M1/M2 系列芯片，利用苹果自研 GPU 加速。
  • cpu：无专用 GPU 时使用，训练速度较慢）。

四、定义神经网络模型

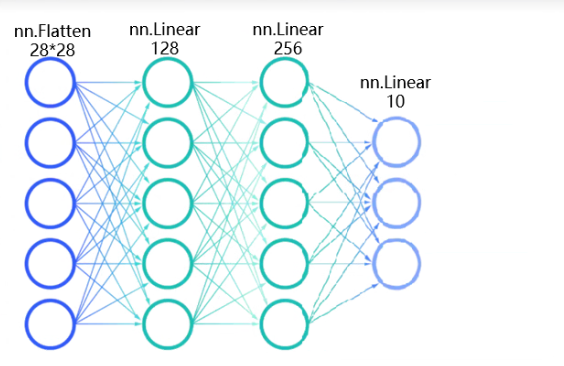
本文设计一个简单的三层全连接神经网络 ，结构为：输入层→隐藏层 1→隐藏层 2→输出层。全连接层（nn.Linear）的核心是矩阵乘法，将前一层的特征映射到后一层。

1.模型定义代码

python 复制代码 
class NeuralNetwork(nn.Module):
    def __init__(self):
        super().__init__()
        self.flatten = nn.Flatten()
        self.hidden1 = nn.Linear(28 * 28, 128)
        self.hidden2 = nn.Linear(128, 256)
        self.out = nn.Linear(256, 10)

    # 前向传播：定义数据在模型中的流动路径
    def forward(self, x):
        x = self.flatten(x)
        x = self.hidden1(x)
        x = torch.sigmoid(x)
        x = self.hidden2(x)
        x = torch.sigmoid(x)
        x = self.out(x)
        return x

# 创建模型实例并移动到指定设备
model = NeuralNetwork().to(device)
print(model)

2.模型结构输出与解析

运行后会打印模型结构：

python 复制代码 
NeuralNetwork(
  (flatten): Flatten(start_dim=1, end_dim=-1)
  (hidden1): Linear(in_features=784, out_features=128, bias=True)
  (hidden2): Linear(in_features=128, out_features=256, bias=True)
  (out): Linear(in_features=256, out_features=10, bias=True)
)
关键组件解析
  1. nn.Flatten ：将输入从[N, C, H, W]展平为[N, C×H×W]，消除空间维度，适配全连接层的一维输入要求。
  2. nn.Linear(in_features, out_features) ：全连接层，本质是矩阵乘法：output = x × weight + bias，其中weight（权重）和bias（偏置）是模型需要学习的参数。
    • 例如隐藏层 1：输入 784 维，输出 128 维，对应权重矩阵形状为[784, 128]，偏置向量形状为[128]。
  3. torch.sigmoid(x) ：激活函数，将输入值压缩到0-1区间，为模型引入非线性（若没有激活函数，多层全连接等价于单层，无法学习复杂规律）。
  4. 输出层：输出 10 维向量，对应每个数字类别的 "原始分数"（未归一化的概率），后续通过损失函数自动转换为概率。

3. 定义训练与测试函数

训练函数负责 "教模型学习"，测试函数负责 "检验学习效果"：

python 复制代码 
def train(dataloader, model, loss_fn, optimizer):
    model.train()  #告诉模型开始训练，pytorch提供2种房市来切换训练和测试模式
                    #训练 model.train()   测试model.eval()
    batch_count = 1  # 记录批次号

        for X,y in dataloader:
        X,y = X.to(device),y.to(device)
        pre = model.forward(X)
        loss = loss_fn(pre,y)
        optimizer.zero_grad()  #清空梯度
        loss.backward()        #反向传播计算梯度
        optimizer.step()       #更新模型参数

        loss_value = loss.item()     #获取损失值的python数值
        if batch_size_num%100 == 0:  #每100个批次打印一次损失值
            print(f"loss:{loss_value:>7f} [number:{batch_size_num}]")
        batch_size_num+=1

def test(dataloader, model, loss_fn):
    model.eval()  # 切换到评估模式
    size = len(dataloader.dataset)  # 获取测试集总样本数
    num_batches = len(dataloader)  # 获取批次数量
    test_loss, correct = 0, 0  # 初始化总损失和正确预测数

    with torch.no_grad():  # 禁用梯度计算，节省内存和计算资源
        for X, y in dataloader:
            X, y = X.to(device), y.to(device)  # 将数据移动到设备
            pred = model(X)  # 前向传播获取预测值
            test_loss += loss_fn(pred, y).item()  # 累加损失值
            correct += (pred.argmax(1) == y).type(torch.float).sum().item()  # 统计正确预测数

    test_loss /= num_batches  # 计算平均损失
    correct /= size  # 计算正确率
    print(f"Test Error: \n Accuracy: {(100 * correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")

4. 配置训练参数并执行

python 复制代码 
loss_fn = nn.CrossEntropyLoss()  #nn.CrossEntropyLoss(): 定义交叉熵损失函数（适用于分类问题）
optimizer = torch.optim.SGD(model.parameters(),lr=0.01)   #torch.optim.SGD: 使用随机梯度下降优化器
train(train_dataloader,model,loss_fn,optimizer)


epochs = 10
for t in range(epochs):
    print(f'Epoch{t+1}\n')
    train(train_dataloader,model,loss_fn,optimizer)
print('Done')
test(test_dataloader,model,loss_fn)

原代码预期结果：使用 Sigmoid 激活函数，100轮训练后准确率约98%，但训练后期损失下降缓慢 ------ 这正是 Sigmoid 的缺陷导致的，我们将在下文分析。

五、梯度消失与梯度爆炸：原理与解决方案

在原代码中，Sigmoid 激活函数导致训练后期损失下降缓慢，本质是梯度消失------ 这是深度学习中阻碍模型训练的核心问题之一。我们从原理、现象、解决方案三方面展开。

1. 梯度消失（Vanishing Gradient）

（1）原理：链式法则的 "乘积衰减"

神经网络的梯度通过链式法则反向传播，即：

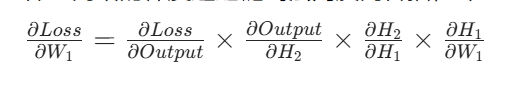
其中，H1、H2是隐藏层输出，W1是输入层到隐藏层 1 的权重。

以 Sigmoid 为例 Sigmoid 的导数最大值仅为0.25（当 x=0 时）。若网络有 5 层隐藏层，每层导数取 0.25，则梯度经过 5 层传播后：0.25^5 = 0.00097656 梯度已衰减到原来的 1/1000 以下 ------ 这就是梯度消失：浅层网络（靠近输入层）的梯度几乎为 0，参数无法更新，模型停止学习。

2. 梯度爆炸（Exploding Gradient）

（1）原理：链式法则的 "乘积放大"

与梯度消失相反，若各层梯度的乘积大于 1，则梯度会指数级增长：

  • 例如，权重初始化过大（如 W 的均值为 2），激活函数导数为 1，则 5 层后梯度为2^5=32，10 层后为2^10=1024；
  • 梯度值过大，会导致参数更新时 "一步跨度过大"，甚至出现 NaN（数值溢出）。

3. 解决方案

替换激活函数为RELU激活函数

ReLU 的数学定义与导数特性
1. ReLU 的数学公式

ReLU 是一个极其简单的分段函数，定义为： ReLU(x)=max(0,x)

  • 当输入x>=0时，y = x;
  • 当输入x < 0 时，y = 0

导数为：

  • 当输入x>0时，y '= 1;
  • 当输入x < 0 时，y '= 0
（1）x > 0 时，导数恒为1------避免梯度消失

当隐藏层神经元的输入 x > 0 时，ReLU的导数为1。此时，梯度在反向传播过程中：

  • 各层激活函数导数的乘积为 1*1*1*1....*1=1；
  • 梯度不会因为"多层传播"而衰减，浅层参数（如输入层→第1隐藏层的权重）能获得有效的梯度更新。
（2）导数范围被限制在{0, 1}------避免梯度爆炸

梯度爆炸的核心是"梯度乘积大于1，导致指数级增长",而ReLU的导数只有两个可能值：0或1。无论网络有多少层，各层导数的乘积最大为1， 而ReLU的导数只有两个可能值：0或1。无论网络有多少层，各层导数的乘积最大为1。

代码示例：

python 复制代码 
    def forward(self,x):
        x = self.flatten(x)
        x = self.hidden1(x)
        x = torch.relu(x)
        x = self.hidden2(x)
        x = torch.relu(x)
        x = self.out(x)
        return x

relu激活函数可能在比较少的网络层中作用不大，但是当网络层数量大的时候，relu函数可以体现出较为重要的作用。

热门推荐
01UV安装并设置国内源02KGG转MP3工具|非KGM文件|解密音频03不再让Windows更新！&Edge游戏助手卸载及关闭自动更新04Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code05【2025.08.06最新版】Android Studio下载、安装及配置记录（自动下载sdk）06Claude Code VSCode集成开发指南：AI编程助手完整配置07突破百度网盘的下载限速，两种方法教会你【超详细】08jdk21下载、安装（Windows、Linux、macOS）09Linux下V2Ray安装配置指南10如何在Windows/Linux系统上安装adb