A. Painting With Two Colors

思路:题意是说有n个单元格,然后让你先涂连续的x个红色,然后再涂y个蓝色,然后问你能否让n个单元格处于一种对称的状态,我们通过分析可知,如果n的奇偶性和x和y的奇偶性一样的话,那么肯定是可以对称的,如果n的奇偶性和x的奇偶性不同和y的奇偶性一样,如果y可以覆盖x,可以直接用y来覆盖x也是可以对称的别的就是没法对称了
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n,a,b;
void solve()
{
cin >> n >> a >> b;
if(n%2==a%2&&a%2==b%2)
{
cout << "YES\n";
}
else if(n%2!=a%2)
{
if(b>a&&b%2==n%2)
{
cout << "YES\n";
}
else
{
cout << "NO\n";
}
}
else
{
cout << "NO\n";
}
}
signed main()
{
cin >> t;
while(t--)
{
solve();
}
return 0;
}B. Add 0 or K

思路:题意种已经说了给定一个k,然后每次都可以给a[i]这个位置的树选择加k或者0,然后最多加k次,那我们首先对于k是奇数肯定很好想,直接给所有奇数都加成为偶数,但是对于k是偶数的情况,我们就要考虑上面那个东西了,最多加k次,我们能否猜想最后的结果与k有关,我们可以选择加0~k次的k,也就是说明我们的模数应该为(k+1),如果取模(k+1)的数为x,我们就要加x次k即可,然后最终输出最终的结果即可
cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n, k;
int a[2000005];
void solve()
{
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
if(k%2==1)
{
for (int i = 1; i <= n; i++)
{
if(a[i]%2==1)
{
a[i] += k;
}
}
for (int i = 1; i <= n; i++)
{
cout << a[i] << " ";
}
cout << "\n";
}
else
{
int flag[n + 1];
for (int i = 1; i <= n;i++)
{
flag[i] = a[i] % (k+1);
}
for (int i = 1; i <= n;i++)
{
a[i]+=flag[i]*k;
}
for (int i = 1; i <= n; i++)
{
cout << a[i] << " ";
}
cout << "\n";
}
}
signed main()
{
int t;
cin >> t;
while(t--)
{
solve();
}
}C. Even Larger

思路:题意的意思说不论任何的字段都不能出现偶数位上的和小于奇数位上的和,因此我们可以将段数划分一下,可以拆分成x个长度为2的段和y个长度为3的段,因此我们只需要去处理2和3的小段就可以了
1.处理2的小段,我们去遍历偶数下标,其左右的奇数下标只能为值只能为min(a[奇数],a[偶数])
2.处理3的小段,我们还是去遍历偶数下标,但是要处理一个条件i+1<n这个条件,然后去判断左右奇数下表之和是否大于这个偶数下标的数,如果大于,就先去减去右边的奇数
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
int n;
int a[2000005];
void solve()
{
cin >> n;
for (int i = 1; i <= n; i++)
{
cin >> a[i];
}
int ans = 0;
for (int i = 2; i <= n; i += 2)
{
if (a[i - 1] > a[i] && i - 1 >= 1)
{
ans += a[i - 1] - a[i];
a[i - 1] = a[i];
}
if (a[i + 1] > a[i] && i + 1 <= n)
{
ans += a[i + 1] - a[i];
a[i + 1] = a[i];
}
}
for (int i = 2; i <= n; i += 2)
{
if (a[i - 1] + a[i + 1] >= a[i] && a[i - 1] >= 1 &&i + 1 <= n)
{
int cha = a[i - 1] + a[i + 1] - a[i];
if (a[i + 1] >= cha)
{
a[i + 1] -= cha;
ans += cha;
}
else
{
a[i + 1] = 0;
cha -= a[i + 1];
a[i - 1] -= cha;
ans += cha;
}
}
}
cout << ans << "\n";
}
signed main()
{
int t;
cin >> t;
while (t--)
{
solve();
}
return 0;
}D. Sliding Tree
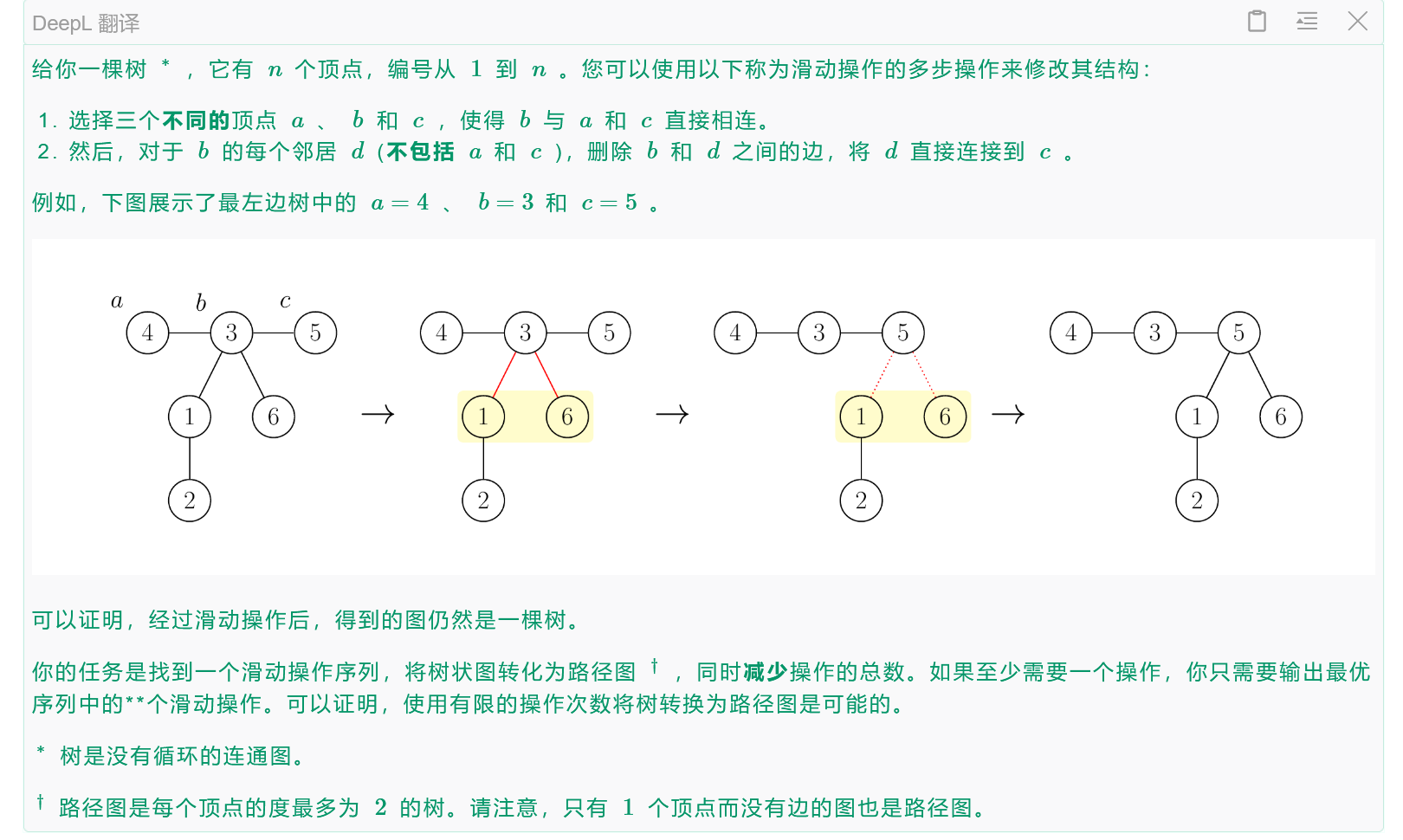
思路:我们这题其实真正的操作就是想让你把一整颗树变成一个链,我们通过上述阐述的操作会发现这种操作会增加树的直径增加1
因此对于这题我们不仅可以求出来树的最少操作次数为(n-1)-L(L表示树的直径),然后我们来考虑怎样去设置a,b,c的点位才能够让树的直径+1,通过上面那个图,我们发现b一定会在树的直径上,并且c一定在树的直径外的分支上,因此我们可以知道a其实就是b的父节点,因此我们可以先找到树的直径,如果直径长度为n-1(因为根节点在0深度,所以最长直径深度为n-1),则直接输出-1,否则我们会去遍历所有节点,首先判断当且节点是否在树的直径,是否有儿子节点不在树的直径,并且其父亲节点的值不为-1,如果有就直接输出即可
cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
int t;
int n, u, v;
int fa[200005];
vector<int> e[200005];
int dis[200005];
void dfs(int u, int par)
{
fa[u] = par;
for (int v : e[u])
{
if (v != par)
{
dis[v] = dis[u] + 1;
dfs(v, u);
}
}
}
void solve()
{
cin >> n;
for (int i = 1; i < n; i++)
{
cin >> u >> v;
e[u - 1].push_back(v - 1);
e[v - 1].push_back(u - 1);
}
dis[0] = 0;
dfs(0, -1);
int flag = 0;
for (int i = 0; i < n; i++)
{
if (dis[i] > dis[flag])
{
flag = i;
}
}
dis[flag] = 0;
dfs(flag, -1);
flag = 0;
for (int i = 0; i < n; i++)
{
if (dis[i] > dis[flag])
{
flag = i;
}
}
if (dis[flag] == n - 1)
{
cout << "-1\n";
}
else
{
int is_zhi[n];
for (int i = 0; i < n; i++)
{
is_zhi[i] = 0;
}
int cur = flag;
while (cur != -1)
{
is_zhi[cur] = 1;
cur = fa[cur];
}
int a = -1, b = -1, c = -1;
for (int u = 0; u < n; u++)
{
for (int v : e[u])
{
if (is_zhi[u] == 1 && is_zhi[v] == 0)
{
a = fa[u];
b = u;
c = v;
break;
}
}
if (a != -1)
break;
}
cout << a + 1 << " " << b + 1 << " " << c + 1 << "\n";
}
for (int i = 0; i <= n; i++)
{
e[i].clear();
dis[i] = 0;
fa[i] = -1;
}
}
signed main()
{
cin >> t;
while (t--)
{
solve();
}
return 0;
}