一、核心目标与核心概念
1. 基本需求与理想超平面
- 基本需求 :在样本空间中找到一个划分超平面,将不同类别的样本完全分离。
- 超平面定义:n 维空间的超平面是 n-1 维子空间,由 n 维向量w(法向量)和实数b(截距)定义,方程为wTx+b=0。例如:
- 3 维空间中,超平面是 2 维平面;
- 2 维空间中,超平面是 1 维直线。
- 理想超平面标准 :对训练样本局部扰动的 "容忍性" 最好,即最大化 margin(间隔)------ 超平面到两侧最近样本点的距离之和margin=2d,d 为超平面到单侧最近样本的距离)。
- 支持向量:距离超平面最近的样本点,是决定超平面位置的关键(其他样本点对超平面无影响)。
2. 点到超平面的距离

二、SVM 优化目标与转化
1. 数据集与决策方程

2. 优化目标转化

三、优化求解:拉格朗日乘子法与对偶问题
1. 拉格朗日函数构造

2. 对偶问题转化与求解

3. 求解实例核心结论

四、关键拓展:软间隔与核函数
1. 软间隔:处理噪音样本

2. 核函数:解决低维不可分


绘制决策边界函数,绘图时对数据进行 PCA 降维到 2 维
def plot_split_line(model, X_scaled, y, title, ax):
先对原始标准化后的特征进行 PCA 降维到 2 维,用于可视化
pca = PCA(n_components=2, random_state=42)
X_pca = pca.fit_transform(X_scaled)
h = 0.02
x_min, x_max = X_pca[:, 0].min() - 1, X_pca[:, 0].max() + 1
y_min, y_max = X_pca[:, 1].min() - 1, X_pca[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
为了用训练好的模型预测网格点,需要构造虚拟的 30 维特征(填充 0 ,仅为匹配模型输入维度)
grid_points_2d = np.c_[xx.ravel(), yy.ravel()]
grid_points_30d = np.hstack([grid_points_2d, np.zeros((len(grid_points_2d), X_train_scaled.shape[1] - 2))])
使用训练好的模型进行预测
Z = model.predict(grid_points_30d)
Z = Z.reshape(xx.shape)
绘图
ax.contourf(xx, yy, Z, alpha=0.3, cmap=plt.cm.coolwarm)
ax.scatter(X_pca[y==0, 0], X_pca[y==0, 1], c='red', label='恶性肿瘤(0)', edgecolors='k')
ax.scatter(X_pca[y==1, 0], X_pca[y==1, 1], c='blue', label='良性肿瘤(1)', edgecolors='k')
绘制支持向量(先获取 30 维的支持向量,再降维到 2 维展示)
support_vectors_30d = model.support_vectors_
support_vectors_2d = pca.transform(support_vectors_30d)
ax.scatter(support_vectors_2d[:, 0], support_vectors_2d[:, 1],
facecolors='none', edgecolors='black', s=100, label='支持向量')
ax.set_title(title)
ax.set_xlabel(f'PCA主成分1(解释方差:{pca.explained_variance_ratio_[0]:.2%})')
ax.set_ylabel(f'PCA主成分2(解释方差:{pca.explained_variance_ratio_[1]:.2%})')
ax.legend()
7. 创建画布并绘制对比图,展示不同核函数、不同 C 值的模型
fig, axes = plt.subplots(1, 3, figsize=(18, 10)) # 2 行 3 列布局展示 6 个模型
axes = axes.ravel() # 展平为一维数组方便遍历
for i, (name, model) in enumerate(svm_models.items()):
plot_split_line(
model=model,
X_scaled=X_train_scaled, # 传入原始标准化后的 30 维特征
y=y_train,
title=name, ax=axes[i]
)
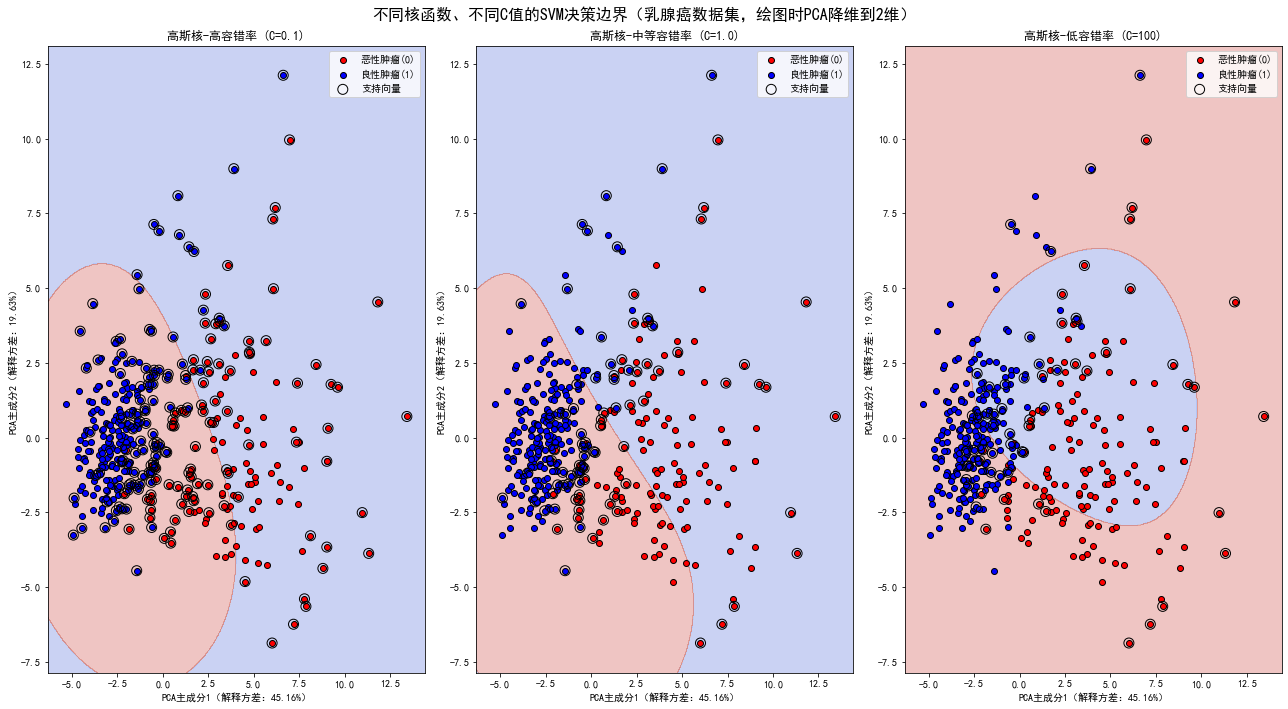
fig.suptitle('不同核函数、不同C值的SVM决策边界(乳腺癌数据集,绘图时PCA降维到2维)', fontsize=16)
plt.tight_layout()
plt.show()