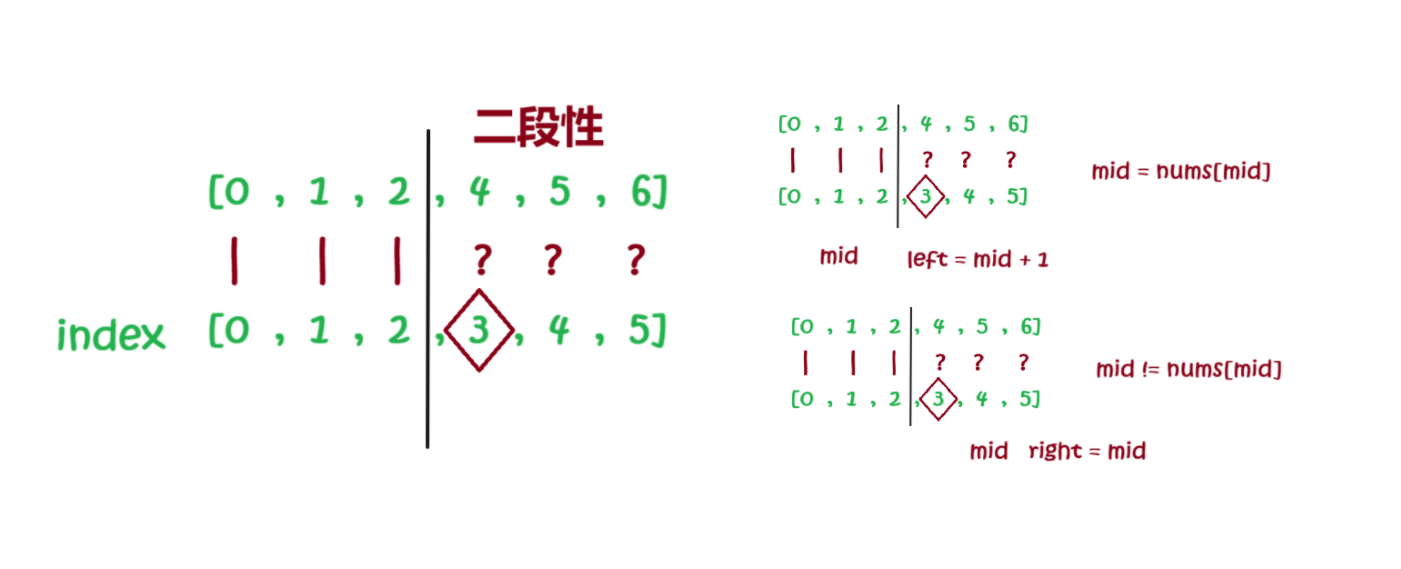
二分
二分算法的特点是最恶心,细节最多,最容易写出死循环的算法,但是理解之后,就是最简单的!(我们在做题过程中,一定要细心画)
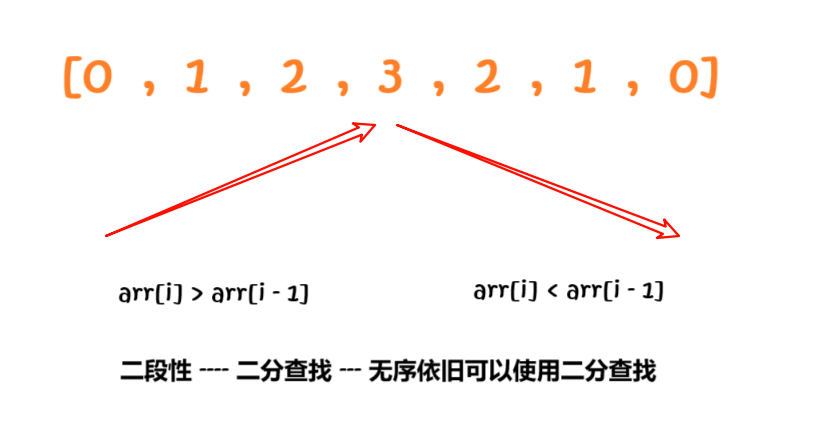
我们经常听:当数组有序的时候,我们才可以使用二分查找算法,但是当我们真正的理解其算法原理之后,我们才会发现,二分算法是很厉害的算法,不仅仅是数组有序的时候使用,即使数组无序的情况,只要我们能发现一些规律,也是可以使用二分查找算法的!
二分算法主要适用于 单调性问题 或 具有二段性(可二分性)的问题,即通过某个条件可以将问题划分为两个连续的部分(一部分满足条件,另一部分不满足),从而通过二分快速定位目标值或边界。
对于二段性,我们可以通过示例来分段,是否可行,对于一些题目,我们可以通过函数图像来分析!
适用二分算法的题目类型:
在有序数组中查找目标值 (经典二分查找):例如:给定升序数组 nums 和目标值 target,找到 target 的索引。
寻找边界(第一个/最后一个满足条件的元素) :例如:在有序数组中找到 target 的第一次出现位置(左边界)或最后一次出现位置(右边界)。
最大值最小化/最小值最大化问题 (二分答案):问题可以转化为:假设答案为 x,判断 x 是否可行,且 x 的取值范围具有单调性(若 x 可行,则比 x 更大/更小的值也可行或不可行)。
典型例子:
分割数组的最大值(将数组分成 k 段,使子数组和的最大值最小)。
在 D 天内送达包裹的能力(传送带每天运送能力为 x,判断能否在 D 天内运完所有包裹,求最小 x)。
制作 m 束花所需的最少天数(花需要连续开放 k 天才能制作一束,求最小天数使得能制作 m 束)。
旋转排序数组中的查找 (利用二段性):例如:搜索旋转排序数组(如 [4,5,6,7,0,1,2]),虽然整体无序,但总有一侧是有序的,可以通过二分缩小范围。
未排序但具有二段性的问题 (如峰值查找、山脉数组等):例如:寻找峰值(nums[i] > nums[i-1] && nums[i] > nums[i+1]),通过比较中间元素与相邻元素判断峰值在哪一侧。
核心思路:
二分的本质是逐步缩小搜索范围,通过判断中间元素与目标条件的关系,确定目标在左半部分还是右半部分。
关键点:
-
确定搜索区间(左闭右闭
[left, right]或左闭右开[left, right))。 -
定义
check(mid)函数(判断中间值是否满足条件,从而决定如何移动边界)。 -
注意终止条件(避免死循环),通常
while (left <= right)或while (left < right)。
总结:
只要问题可以转化为"在单调序列中查找"或"具有二段性(可通过某个条件将区间一分为二)",就可以考虑二分算法。常见于查找目标值、边界、二分答案(最值问题)等场景。
也就是说不管数组有无顺序,只要当我们发现一个规律,我们根据这个规律选取一个点之后,能将这个数组分成两部分,根据规律能有选择性的减去一部分,然后去另一部分查找,此时我们就可以使用二分查找算法,这就是二段性!
我们可以选择中间位置,三分之一位置,四分之一位置...来进行抽象!只要能分成两部分就可以了!但是根据概率学,我们中间部分是更好的!
模板(不要死记硬背,核心要理解)解决99.9%的二分题
朴素的二分模板(下面第一题)(简单)
cpp
细节:left > right 的时候结束循环
left <= right --- 持续循环查找
x < t left = mid + 1 --> [mid + 1, right]
x > t right = mid - 1 --> [left, mid - 1]
x == t --> return mid
mid = left + ((right - left) >> 1);
在于 + 的优先级高于 >>(右移运算符)模板就是:
cpp
while(left <= right)//细节,一定是 "<="
{
int mid = left + ((right - left) >> 1);//防溢出风险
int mid = left + ((right - left + 1) >> 1);//防溢出风险//两者等价
if(......)
{
right = mid - 1;
}
else if(......)
{
left = mid + 1;
}
else
{
return ......;
}
}"......"根据题目的二段性,将信息填入到"......"
后面的两个模板是万能的,也可以解决第一个问题,但是细节多的!
查找左边界的二分模板(下面第二题)(up)
html
查找左端点最核心的两步:
x < t -> left = mid + 1 ---> [mid + 1, right]
x >= t -> right = mid ---> [mid, right]
不同点在于更新 right 的时候,要更新到 mid 位置,因为 mid 可能是最终结果
细节处理(最恶心,也最重要):
1. 循环条件 --- left < right(我们根据图也是可以知道的 --- 第二问)
分析:
[------------------------------------]
| || |
l m-1 m r
【 合法区域(left)】 【 合法区域(right)】
i. 有结果 :right 永远在合法区间内,但是left=mid+1,是想要跳出合法区域,
所以当left=right的时候,就是最终结果,没有必要再进去循环!
ii. 全大于 t :只有right会动,会疯狂往left走,知道left=right,没有必要再进入循环!
我们只需要判断nums[letf]的值是否等于t,就可以判断出是否找到!
iii.全小于 t :同理
如果我们使用left<=right就会出现死循环
2. 求重点的操作(求 mid )
对于朴素二分的mid有两种形式:(都可以用)
left + (right - left) / 2 --- 当数组是偶数的时候,求得是靠左的位置
left + (right - left + 1) / 2 --- 当数组是偶数的时候,求得是靠右的位置
但是对于查找左边界:
当数组剩下两个元素【left, right】,我们采用第二种方式求解的话,mid是当前的right位置:
如果x < t, left = mid + 1就会结束循环
如果x >= t, right = mid, 这就会造成死循环!
所以我们对于查找左边界,需要使用 --- left + (right - left) / 2 这种形式
cpp
while(left < right)
{
int mid = left + (right - left) / 2;
if(......) left = mid + 1;
else right = mid;
}查找右边界的二分模板(下面第二题)(up)
html
查找右端点最核心的两步:
x <= t -> left = mid ---> [mid, right]
x > t -> right = mid - 1 ---> [mid - 1, right]
不同点在于更新 right 的时候,要更新到 mid 位置,因为 mid 可能是最终结果
细节处理(最恶心,也最重要):
1. 循环条件 --- left < right(我们根据图也是可以知道的 --- 第二问)
分析:
[------------------------------------]
| || |
l m m+1 r
【 合法区域(left)】 【 合法区域(right)】
i. 有结果 :left 永远在合法区间内,但是right=mid-1,是想要跳出合法区域,
所以当left=right的时候,就是最终结果,没有必要再进去循环!
ii. 全大于 t :只有right会动,会疯狂往left走,知道left=right,没有必要再进入循环!
我们只需要判断nums[letf]的值是否等于t,就可以判断出是否找到!
iii.全小于 t :同理
如果我们使用left<=right就会出现死循环
2. 求重点的操作(求 mid )
对于朴素二分的mid有两种形式:(都可以用)
left + (right - left) / 2 --- 当数组是偶数的时候,求得是靠左的位置
left + (right - left + 1) / 2 --- 当数组是偶数的时候,求得是靠右的位置
但是对于查找右边界:
当数组剩下两个元素【left, right】,我们采用第一种方式求解的话,mid是当前的left位置:
如果x <= t, left = mid就会造成死循环
如果x > t, right = mid - 1, 这就会结束循环!
所以我们对于查找右边界,需要使用 --- left + (right - left + 1) / 2 这种形式
cpp
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(......) left = mid;
else right = mid - 1;
}题目练习
704. 二分查找 - 力扣(LeetCode)
算法流程:
a. 定义 left ,right 指针,分别指向数组的左右区间。
b. 找到待查找区间的中间点 mid,找到之后分三种情况讨论:
i. arr[mid] == target 说明正好找到,返回 mid 的值;
ii. arr[mid] > target 说明 [mid, right] 这段区间都是大于 target 的,因此舍去右边区间,在左边 [left, mid - 1] 的区间继续查找,即让 right = mid - 1 ,然后重复 2 过程;
iii. arr[mid] < target 说明 [left, mid] 这段区间的值都是小于 target 的,因此舍去左边区间,在右边 [mid + 1, right] 区间继续查找,即让 left = mid + 1 ,然后重复 2 过程;
c. 当 left 与 right 错开时,说明整个区间都没有这个数,返回 -1。
cpp
细节:left > right 的时候结束循环
left <= right --- 持续循环查找
x < t left = mid + 1 --> [mid + 1, right]
x > t right = mid - 1 --> [left, mid - 1]
x == t --> return mid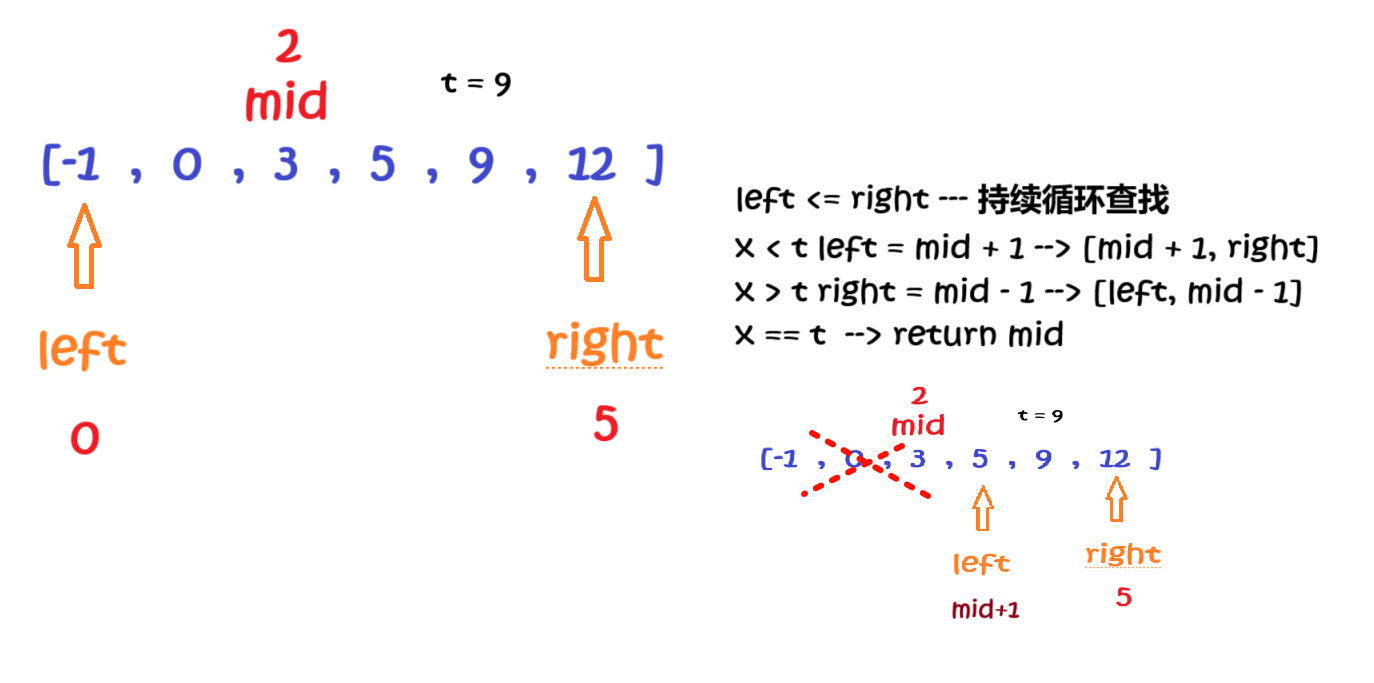
补充:对于中间点,我们使用下面的计算方式是可以防止溢出,并且提高效率的(微乎其微)
cpp
mid = left + ((right - left) >> 1);
在于 + 的优先级高于 >>(右移运算符)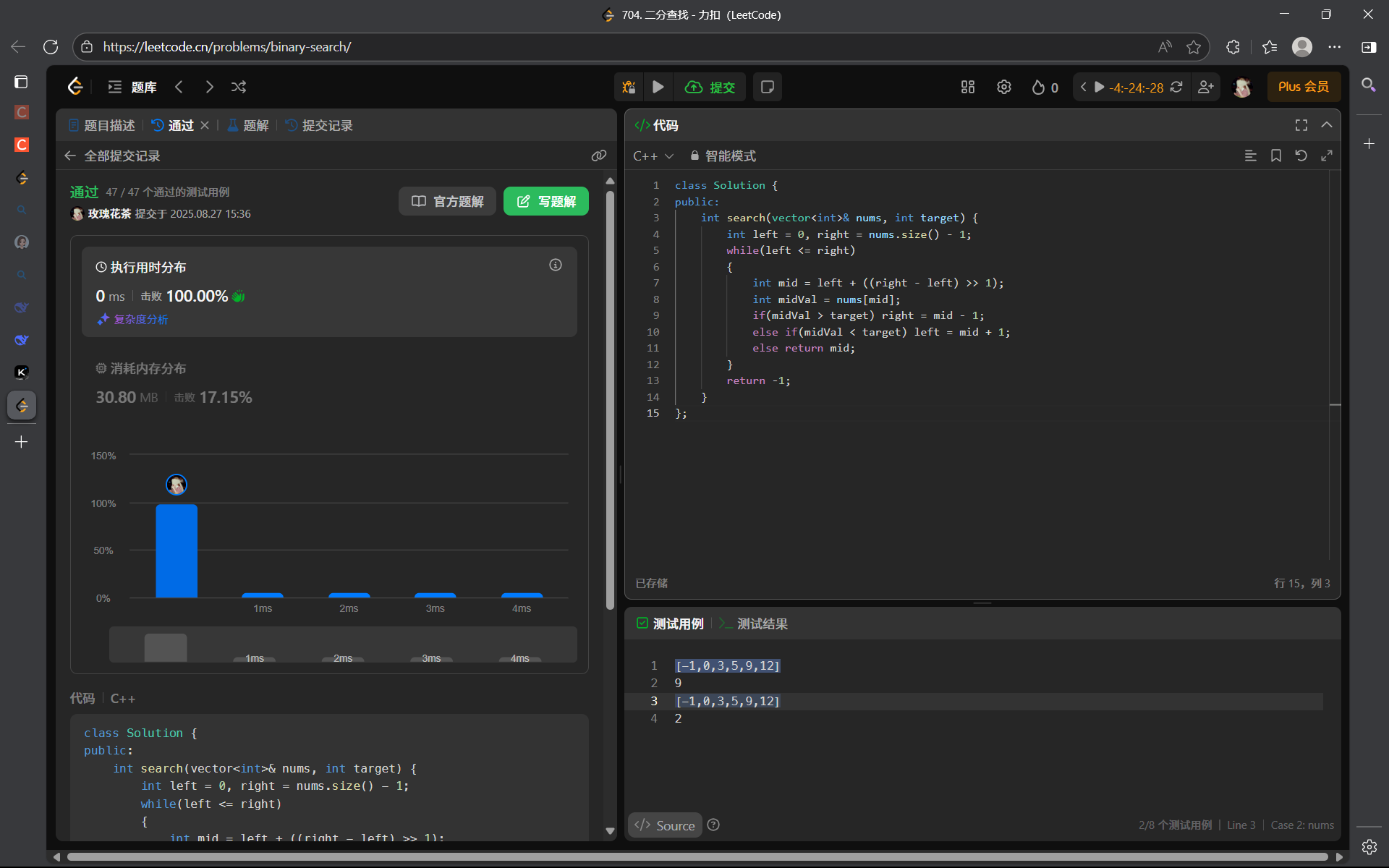
34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣(LeetCode)
算法思路:
二分查找,就是根据数据的性质,在某种判断条件下将区间一分为二,然后舍去其中一个区间,然后再另一个区间内查找。
- 用
x表示该元素,resLeft表示左边界,resRight表示右边界。
寻找左边界思路:
-
我们注意到以左边界划分的两个区间的特点:
-
左边区间
[left, resLeft - 1]都是小于x的; -
右边区间(包括左边界)
[resLeft, right]都是大于等于x的;
-
-
因此,关于
mid的落点,我们可以分下面两种情况:-
当
mid落在[left, resLeft - 1]区间的时候,也就是arr[mid] < target。说明[left, mid]都是可以舍去的,此时更新left到mid + 1,继续在[mid + 1, right]上寻找左边界; -
当
mid落在[resLeft, right]区间的时候,也就是arr[mid] >= target。说明[mid + 1, right](因为mid可能是最终结果,不能舍去)是可以舍去的,此时更新right到mid的位置,继续在[left, mid]上寻找左边界;
-
-
由此,就可以通过二分,来快速寻找左边界。
注意: 这里找中间元素需要向下取整。
因为后续移动左右指针的时候:
-
左指针:
left = mid + 1,是会向后移动的,因此区间是会缩小的; -
右指针:
right = mid,可能会原地踏步(比如:如果向上取整的话,如果剩下 1,2 两个元素,left = 1,right = 2,mid = 2。更新区间之后,left, right, mid的值没有改变,就会陷入死循环)。 -
因此一定要注意,当
right = mid的时候,要向下取整。
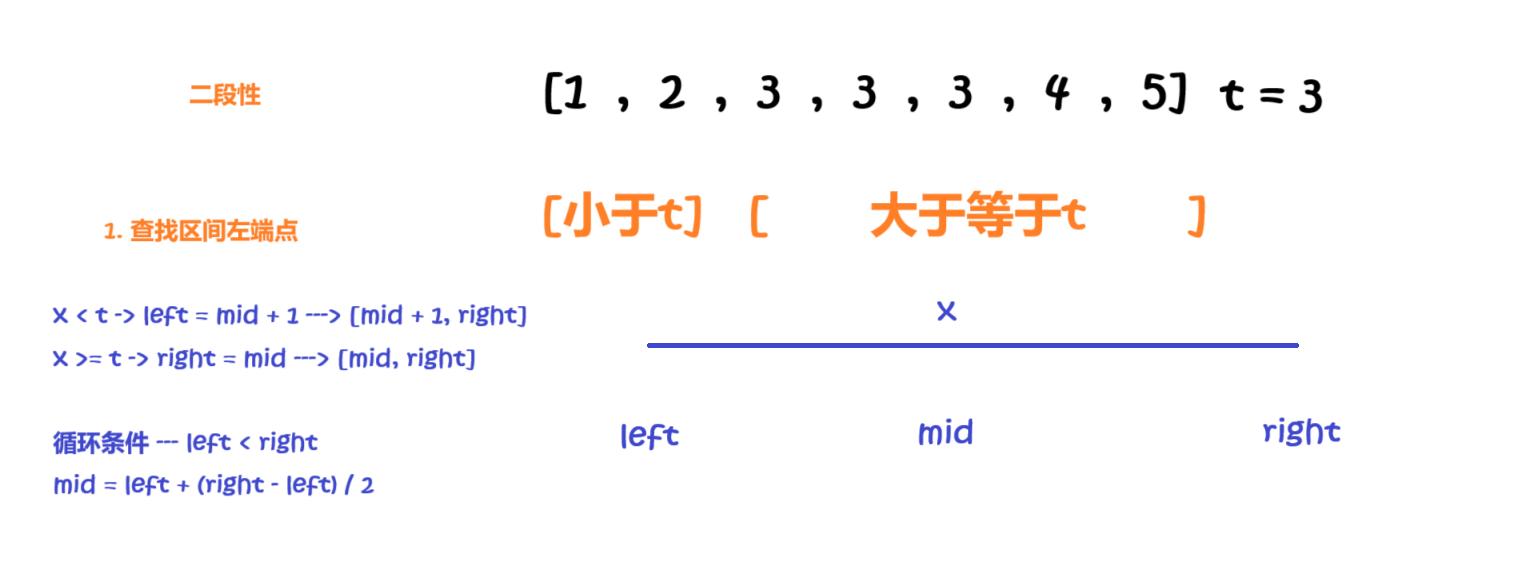
寻找右边界思路:
-
用
resRight表示右边界; -
我们注意到右边界的特点是:
-
右边区间(包括右边界)
[left, resRight]都是小于等于x的; -
左边区间(不包括右边界)
[resRight + 1, right]都是大于x的;
-
-
因此,关于
mid的落点,我们可以分下面两种情况:- 当我们的
mid落在[left, resRight]区间的时候,说明[left, mid - 1](mid不可以舍去,因为可能是最终结果)都是可以舍去的,此时更新left到mid + 1。当mid落在[resRight + 1, right]的区间的时候,说明[mid, right]内的元素是可以舍去的,此时更新right到mid - 1的位置;
- 当我们的
-
由此,就可以通过二分,来快速寻找右边界。

注意: 这里找中间元素需要向上取整。
因为后续移动左右指针的时候:
-
左指针:
left = mid,可能会原地踏步(比如:如果向下取整的话,如果剩下 1,2 两个元素,left = 1,right = 2,mid = 1。更新区间之后,left, right, mid的值没有改变,就会陷入死循环)。 -
右指针:
right = mid - 1,是会向前移动的,因此区间是会缩小的; -
因此一定要注意,当
right = mid的时候,要向下取整。
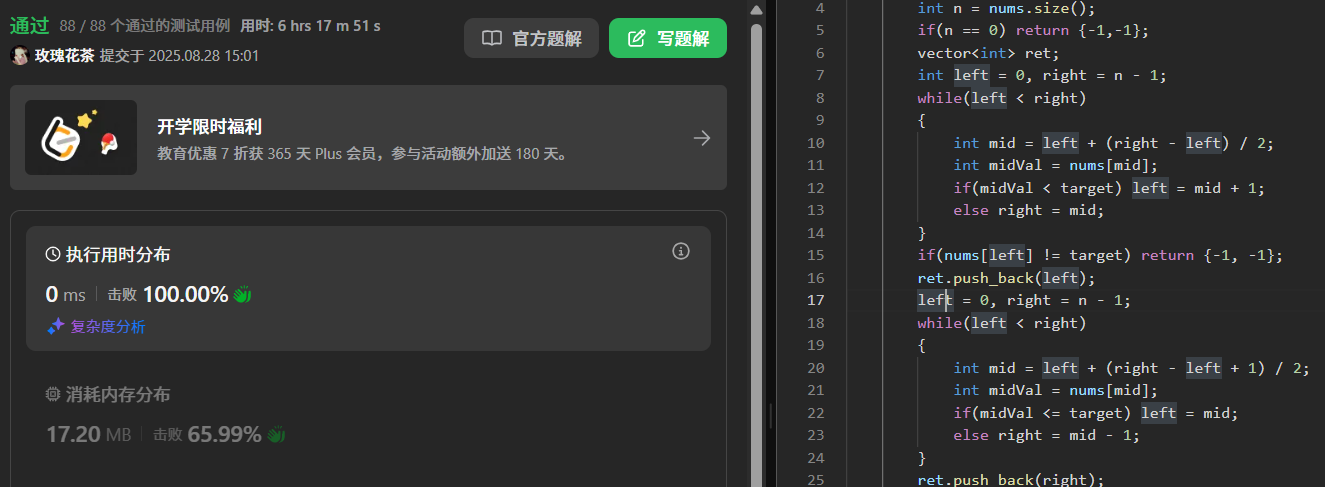
cpp
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int n = nums.size();
if(n == 0) return {-1,-1};
vector<int> ret;
int left = 0, right = n - 1;
while(left < right)
{
int mid = left + (right - left) / 2;
int midVal = nums[mid];
if(midVal < target) left = mid + 1;
else right = mid;
}
if(nums[left] != target) return {-1, -1};
ret.push_back(left);
left = 0, right = n - 1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
int midVal = nums[mid];
if(midVal <= target) left = mid;
else right = mid - 1;
}
ret.push_back(right);
return ret;
}
};
二分查找算法总结:
请大家一定不要觉得背下模板就能解决所有二分问题。二分问题最重要的就是分析题意,然后确定查找的区间,根据分析问题来写出二分查找算法的代码。
-
要分析题意,确定搜索区间,不要死记模板,不要看左闭右开什么乱七八糟的理解
-
要分析题意,确定搜索区间,不要死记模板,不要看左闭右开什么乱七八糟的理解
-
要分析题意,确定搜索区间,不要死记模板,不要看左闭右开什么乱七八糟的理解
-
重要的事说三遍。
模板记忆技巧:
-
关于什么时候用三块,还是二段式中的某一个,一定不要强行去用,而是通过具体的问题分析情况,根据查找区间的变化确定指针的转移过程,从而选择一个模板。
-
当选择两段式的策略时:
- 在求
mid的时候,只有right - 1的情况下,才会向上取整(也就是+1取中间数)
- 在求
69. x 的平方根 - 力扣(LeetCode)
解法一(暴力查找):
算法思路:
依次枚举 [0, x] 之间的所有数 j:
-
如果
j * j == x,直接返回x; -
如果
j * j > x,说明之前的一个数是结果,返回j - 1。
由于 j * j 可能超过 int 的最大值,因此使用 long long 类型。
算法代码:
cpp
class Solution {
public:
int mySqrt(int x) {
long long i = 0;
for (i = 0; i <= x; i++) {
if (i * i == x) return i;
if (i * i > x) return i - 1;
}
return -1;
}
};解法二(二分查找算法):
算法思路:
设 x 的平方根的最终结果为 index:
a. 分析 index 左右两次数据的特点:
-
[0, index)之间的元素,平方之后都是小于等于x的; -
[index + 1, x]之间的元素,平方之后都是大于x的。
因此可以使用二分查找算法。

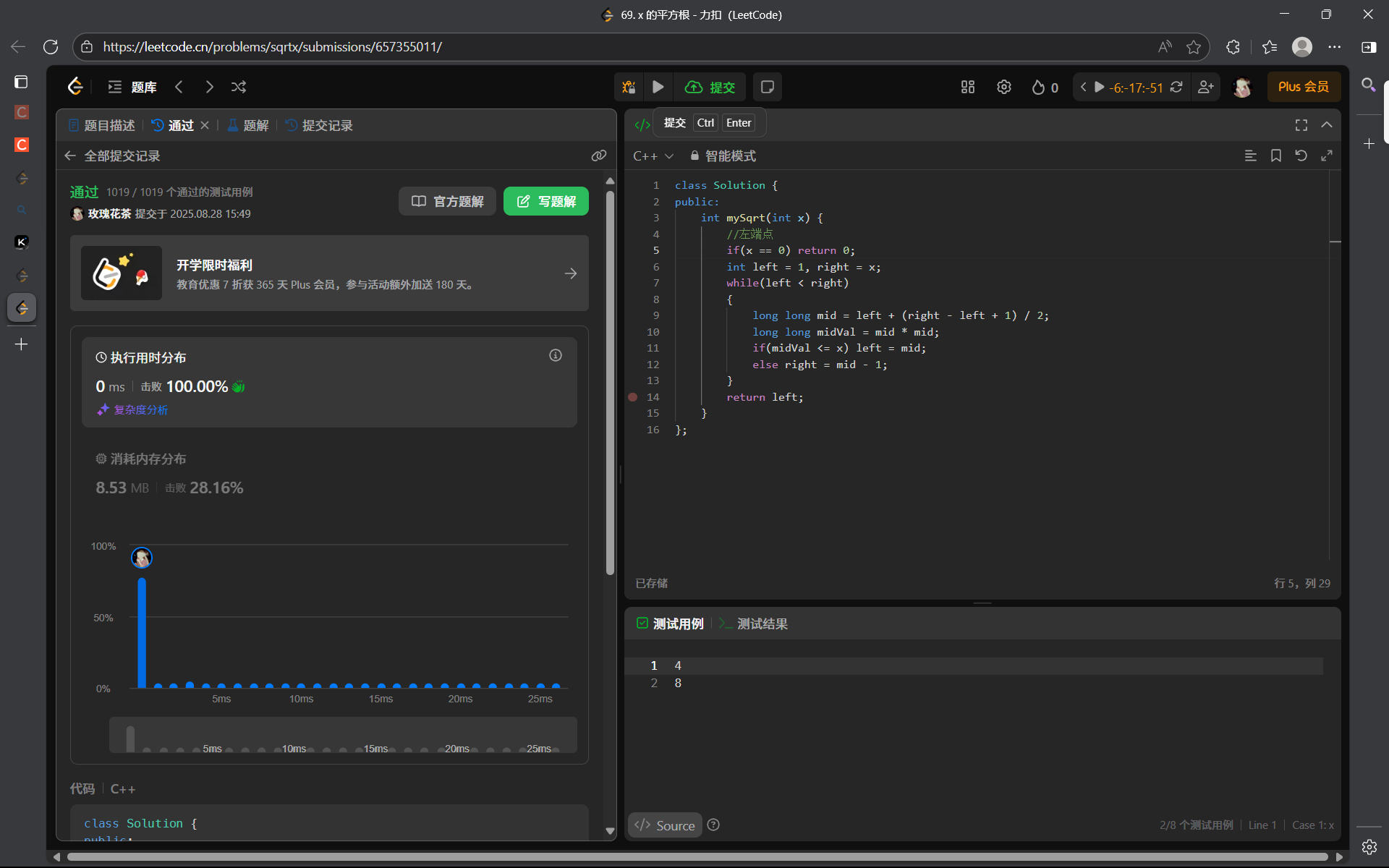
35. 搜索插入位置 - 力扣(LeetCode)
解法(二分查找算法):
算法思路:
a. 分析插入位置左右两侧区间上元素的特点:
设插入位置的坐标为 index,根据插入位置的特点可以知道:
-
[left, index - 1]内的所有元素均是小于target的; -
[index, right]内的所有元素均是大于等于target的。
b. 设 left 为本轮查询的左边界,right 为本轮查询的右边界。根据 mid 位置元素的信息,分析下一轮查询的区间:
-
当
nums[mid] >= target时,说明mid落在了[index, right]区间上,mid左边包括mid本身,可能是最终结果,所以我们接下来查找的区间在[left, mid]上。因此,更新right到mid位置,继续查找。 -
当
nums[mid] < target时,说明mid落在了[left, index - 1]区间上,mid右边但不包括mid本身,可能是最终结果,所以我们接下来查找的区间在[mid + 1, right]上。因此,更新left到mid + 1的位置,继续查找。
c. 直到我们的查找区间的长度变为 1,也就是 left == right 的时候,left 或者 right 所在的位置就是我们要找的结果。
852. 山脉数组的峰顶索引 - 力扣(LeetCode)
解法一(暴力查找):
算法思路:
-
峰顶的特点:比两侧的元素都要大。
-
因此,我们可以遍历数组内的每一个元素,找到某一个元素比两边的元素大即可。
算法代码:
cpp
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int n = arr.size();
// 遍历数组内每一个元素,直到找到峰顶
for (int i = 1; i < n - 1; i++) {
// 峰顶满足的条件
if (arr[i] > arr[i - 1] && arr[i] > arr[i + 1])
return i;
}
return -1;
}
};解法二(二分查找):
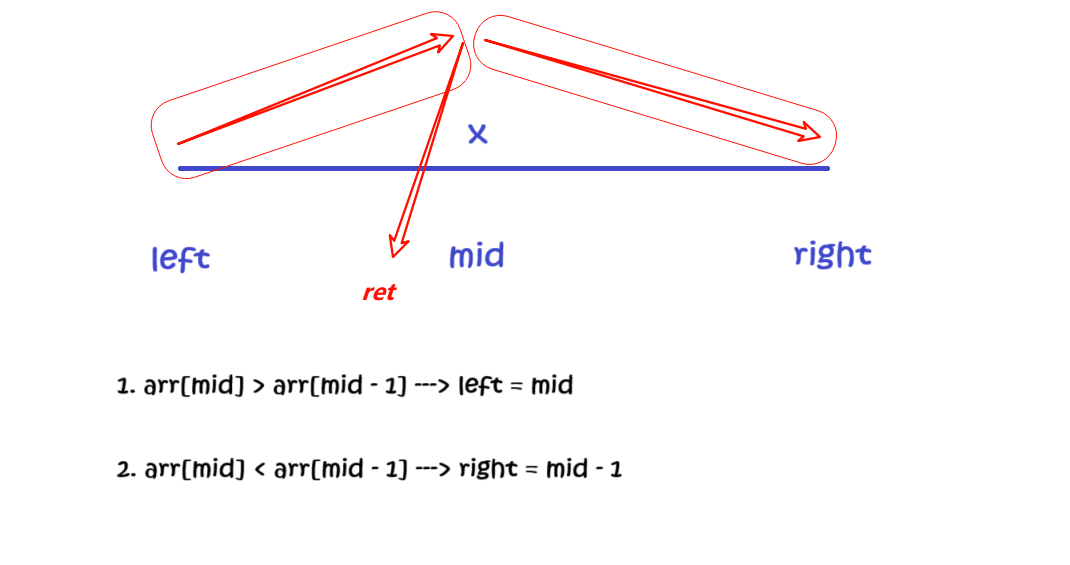
算法思路:
-
分析峰顶位置的数据特点,以及山峰两旁的数据的特点:
-
峰顶数据特点:
arr[i] > arr[i - 1] && arr[i] > arr[i + 1]; -
峰顶左边的数据特点:
arr[i] > arr[i - 1] && arr[i] < arr[i + 1],也就是呈现上升趋势; -
峰顶右边数据的特点:
arr[i] < arr[i - 1] && arr[i] > arr[i + 1],也就是呈现下降趋势。
-
-
因此,根据
mid位置的信息,我们可以分为下面三种情况:-
如果
mid位置呈现上升趋势,说明我们接下来要在[mid + 1, right]区间继续搜索; -
如果
mid位置呈现下降趋势,说明我们接下来要在[left, mid - 1]区间继续搜索; -
如果
mid位置就是山峰,直接返回结果。
-
162. 寻找峰值 - 力扣(LeetCode)
解法二(二分查找算法):
算法思路:
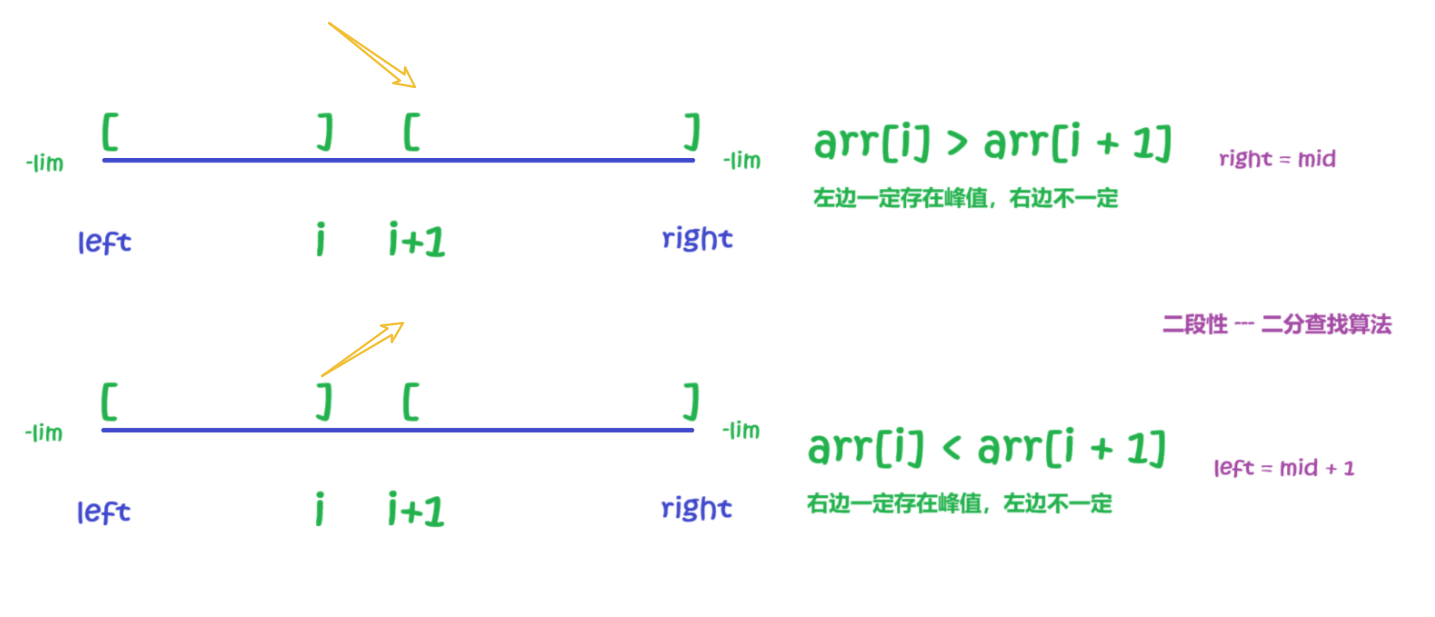
寻找二段性:
任取一个点 i,与下一个点 i + 1,会有如下两种情况:
-
arr[i] > arr[i + 1]:此时「左侧区域」一定会存在山峰(因为最左侧是负无穷),那么我们可以去左侧去寻找结果; -
arr[i] < arr[i + 1]:此时「右侧区域」一定会存在山峰(因为最右侧是负无穷),那么我们可以去右侧去寻找结果。
当我们找到「二段性」的时候,就可以尝试用「二分查找」算法来解决问题。
153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)
解法(二分查找):
算法思路:
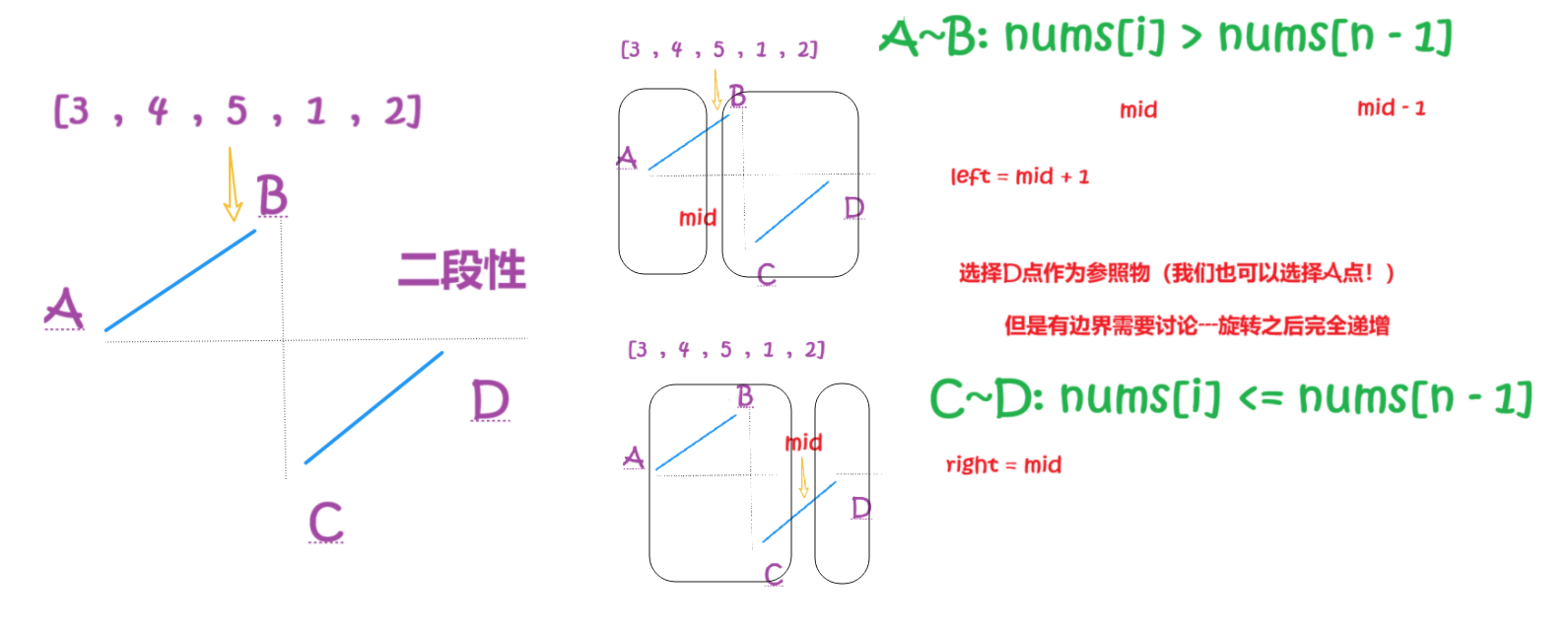
题目中的数组规则如下图所示:
其中 C 点就是我们要求的点。
二分的本质:找到一个判断标准,使得查找区间能够一分为二。
通过图像我们可以发现,[A, B] 区间内的点都是严格大于 D 点的值的,C 点的值是严格小于 D 点的值的。但是当 [C, D] 区间只有一个元素的时候,C 点的值是可能等于 D 点的值的。
因此,初始化左右两个指针 left,right:
然后根据 mid 的落点,我们可以这样划分下一次查询的区间:
-
当
mid在 [A, B] 区间的时候,也就是mid位置的值严格大于 D 点的值,下一次查询区间在 [mid + 1, right] 上; -
当
mid在 [C, D] 区间的时候,也就是mid位置的值严格小于等于 D 点的值,下次查询区间在 [left, mid] 上。
当区间长度变成 1 的时候,就是我们要找的结果。
LCR 173. 点名 - 力扣(LeetCode)
解法(二分查找算法):
算法思路:
关于这道题中,时间复杂度为 O(N) 的解法有很多种,而且也是比较好想的。
- 哈希表
- 直接遍历找结果
- 位运算
- 数学(高斯求和)
本题只讲解一个最优的二分法,来解决这个问题。
在这个升序的数组中,我们发现:
-
在第一个缺失位置的左边,数组内的元素都是与数组的下标相等的;
-
在第一个缺失位置的右边,数组内的元素与数组下标是不相等的。
因此,我们可以利用这个「二段性」,来使用「二分查找」算法。