物理信息神经网络(Physics-Informed Neural Networks, PINNs)是一种结合深度学习与物理定律的神经网络方法,旨在解决涉及偏微分方程(PDEs)的问题。以下是对该问题的详细解答:
-
物理信息神经网络的定义与核心思想
物理信息神经网络(PINNs)是一种将物理定律嵌入到神经网络中的方法,通过将物理方程、边界条件和初始条件作为约束条件,指导神经网络的训练过程。这种方法能够利用已知的物理定律来增强模型的泛化能力,尤其在数据稀缺或数据质量较低的情况下具有显著优势。
-
PINNs的核心机制
• 物理约束的嵌入:PINNs通过将物理方程(如偏微分方程)和边界条件嵌入到神经网络的损失函数中,使模型在训练过程中自动满足物理约束。例如,损失函数通常包括物理残差项和边界条件的残差项。
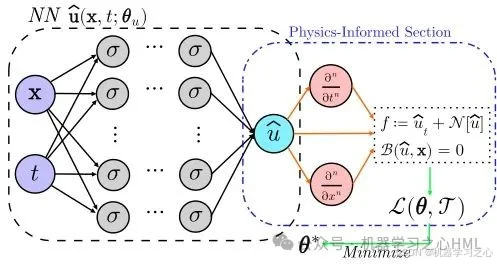
• 数据驱动与物理驱动的结合:PINNs可以同时利用数据和物理知识进行建模,即使在数据量较少的情况下也能获得较好的预测结果。
• 灵活性与可扩展性:PINNs可以处理非线性问题、参数化问题以及多尺度问题,并且能够处理复杂的物理系统,如流体力学、材料科学、地球物理学等。
-
PINNs的应用领域
PINNs在多个领域中得到了广泛应用,包括但不限于: 流体力学与流体动力学:用于模拟流体流动、湍流、波传播等。
一、代码功能
MATLAB 代码实现了一个基于物理信息神经网络(Physics-Informed Neural Network, PINN)的多变量时间序列预测模型,用于对给定的历史数据进行预测,并引入物理约束以提高模型的泛化能力和可解释性。
- 使用历史时间序列数据构建输入-输出对;
- 构建一个带有物理约束的神经网络(PINN);
- 训练网络并评估其在训练集和测试集上的预测性能;
- 输出多种评估指标(RMSE、R²、MAE、MAPE、MBE、MSE);
- 可视化预测结果、误差分布和拟合效果。
二、算法步骤
- 数据导入与重构 :从 Excel 文件中读取数据,构建用于监督学习的样本,每个样本由
kim个历史时刻的特征和zim步后的目标值组成。 - 划分训练集与测试集:按比例(70%)划分数据。
- 数据归一化 :使用
mapminmax将数据归一化到 [0, 1] 区间。 - 转换为 dlarray:将数据转换为深度学习框架可用的格式。
- 生成物理点:随机生成物理点用于物理残差计算。
- 构建 PINN 模型:使用全连接层和 tanh 激活函数构建神经网络。
- 训练模型:使用 Adam 优化器,结合数据损失和物理损失进行训练。
- 预测与反归一化:对训练集和测试集进行预测,并将结果反归一化。
- 评估指标计算:计算 RMSE、R²、MAE、MAPE、MBE、MSE。
- 可视化:绘制预测对比图、误差图、拟合图等。
三、技术路线
- 深度学习框架 :使用 MATLAB 的
dlarray和dlnetwork进行自动微分和网络训练。 - 物理约束:通过物理残差项(Physics Loss)将先验物理知识嵌入损失函数。
- 优化算法:使用 Adam 优化器。
- 评估指标:多种统计指标综合评价模型性能。
四、公式原理

五、参数设定
| 参数名 | 含义 | 取值 |
|---|---|---|
kim |
历史步长 | 4 |
zim |
预测步长 | 1 |
num_size |
训练集比例 | 0.7 |
num_physics |
物理点数量 | 1000 |
numEpochs |
训练轮数 | 1000 |
learningRate |
学习率 | 0.001 |
lambda_phys |
物理损失权重 | 0.1 |
六、运行环境
- 软件:MATLAB2024b(需安装 Deep Learning Toolbox)
- 数据格式 :Excel 文件(
data.xlsx)
七、预测效果
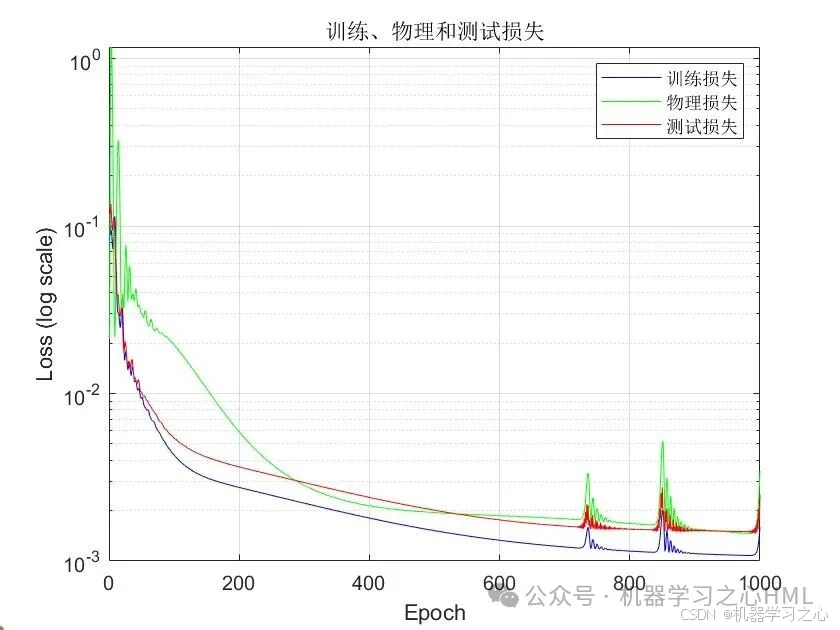
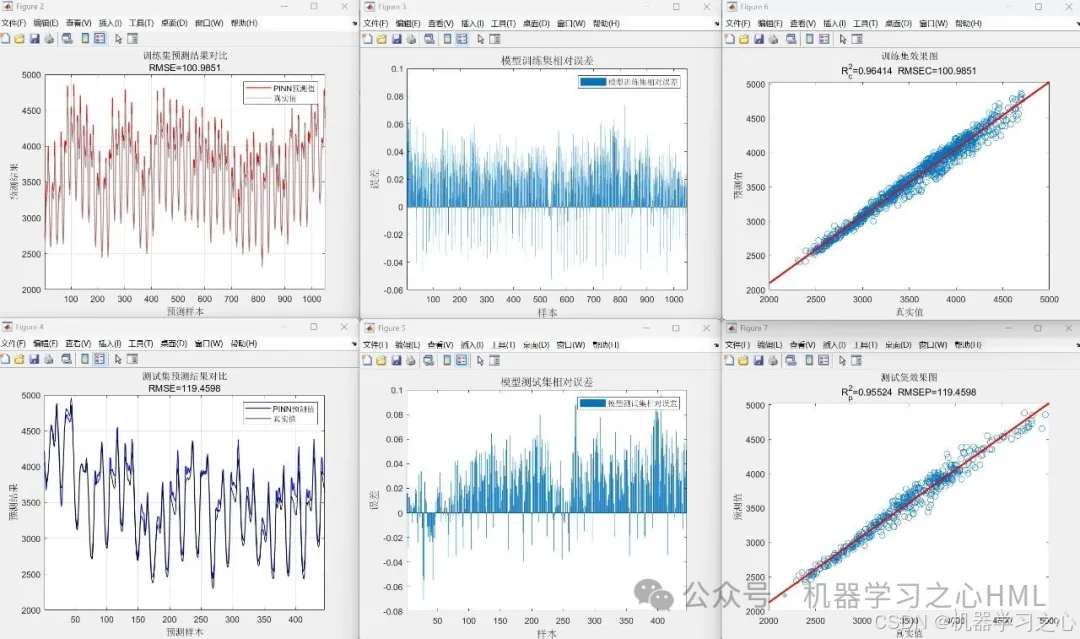
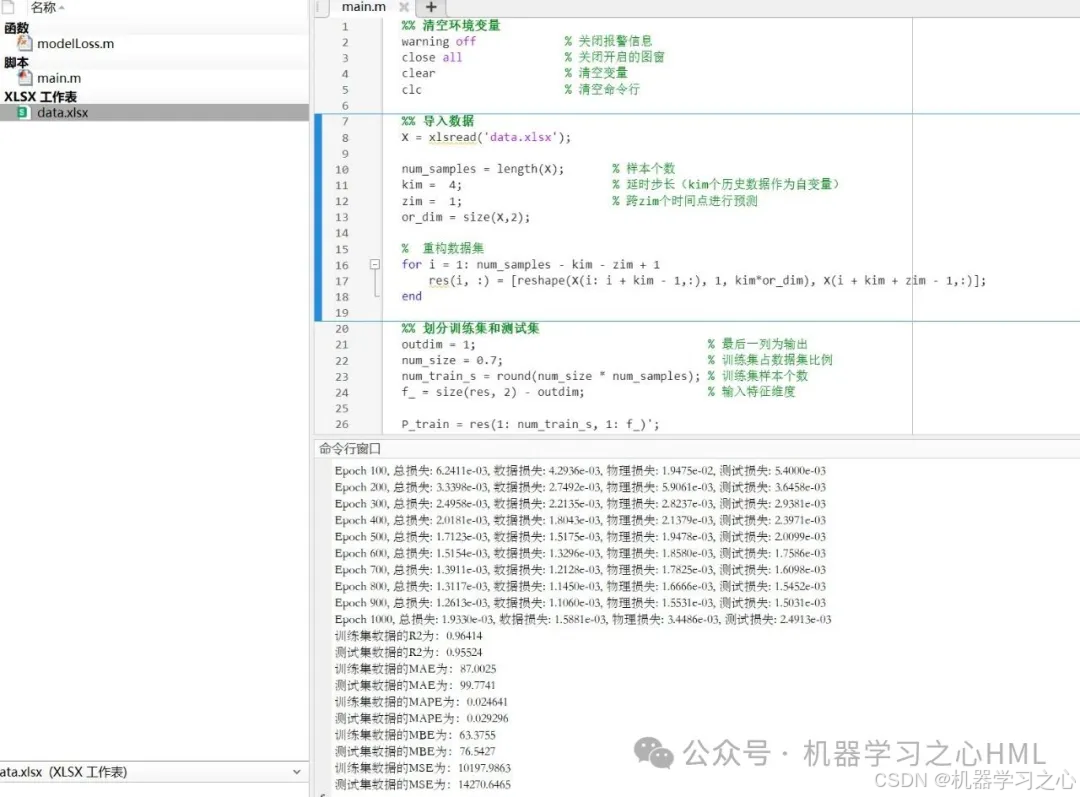
数据集