2025-08-31：可行数组的数目。用go语言，给定一个长度为 n 的初始数组（记作原数组）和一个包含 n 个闭区间的列表（第 i 个区间为 [ui, vi]

2025-08-31：可行数组的数目。用go语言，给定一个长度为 n 的初始数组（记作原数组）和一个包含 n 个闭区间的列表（第 i 个区间为 [ui, vi]）。要求统计所有长度为 n 的候选数组，使得：

候选数组在相邻元素之间的差值序列与原数组完全相同（即对每个 i=1..n-1，候选[i]-候选[i-1] 等于原数组对应的相邻差）。
候选数组的第 i 个元素必须落在第 i 个区间内，ui ≤ 候选[i] ≤ vi。

求满足上述两条约束的候选数组的总数。

2 <= n == original.length <= 100000。

1 <= original[i] <= 1000000000。

bounds.length == n。

bounds[i].length == 2。

1 <= bounds[i][0] <= bounds[i][1] <= 1000000000。

输入：original = [1,2,3,4], bounds = [[1,2],[2,3],[3,4],[4,5]]。

输出：2。

解释：

可能的数组为：

1, 2, 3, 4

2, 3, 4, 5

题目来自力扣3468。

关键观察

候选数组的第一个元素（记为 x0）一旦确定，整个候选数组就被唯一确定（因为相邻差是固定的）。具体来说：
- 候选[0] = x0
- 候选[1] = x0 + (original[1] - original[0])
- 候选[2] = x0 + (original[2] - original[0])
- 一般地，候选[i] = x0 + (original[i] - original[0])
因此，问题转化为：寻找所有实数 x0（实际上是整数，因为数组元素是整数？但题目中边界和原数组都是整数，所以候选数组也是整数），使得对于每个 i，有：
- ui ≤ x0 + (original[i] - original[0]) ≤ vi
定义 a_i = original[i] - original[0]，则约束条件为：
- ui ≤ x0 + a_i ≤ vi 对于每个 i 成立。
这等价于：
- x0 ∈ [ui - a_i, vi - a_i] 对于每个 i。
因此，x0 必须同时满足所有 n 个区间约束（即落在所有区间 [ui - a_i, vi - a_i] 的交集中）。

解决步骤

预处理 ：计算每个位置 i 的 a_i = original[i] - original[0]。注意 a_0 = 0。
转换约束 ：对于每个区间 i，将候选数组第 i 个元素的约束 [ui, vi] 转换为对 x0 的约束：
- 下界：L_i = ui - a_i
- 上界：R_i = vi - a_i
- 即 x0 必须落在 [L_i, R_i] 内。
求交集 ：找出所有区间 [L_i, R_i]（i 从 0 到 n-1）的交集。即：
- 整体下界 L = max(L_0, L_1, ..., L_{n-1})
- 整体上界 R = min(R_0, R_1, ..., R_{n-1})
计算整数解的数量 ：交集 [L, R] 中整数的个数即为候选数组的数量（因为 x0 是整数）。注意：
- 如果 L > R，则交集为空，返回 0。
- 否则，整数解的数量为 R - L + 1。

详细过程

初始化：
- 设 a[0] = 0。
- 对于 i 从 1 到 n-1，计算 a[i] = original[i] - original[0]。
初始化 x0 的全局上下界：
- low = -∞（用最小整数，但实际中可用第一个区间的转换值初始化）
- high = +∞（用最大整数）
遍历每个索引 i（从 0 到 n-1）：
- 计算当前区间对 x0 的约束： L_i = bounds[i][0] - a[i] R_i = bounds[i][1] - a[i]
- 更新全局下界：low = max(low, L_i)
- 更新全局上界：high = min(high, R_i)
检查交集是否非空：
- 如果 low > high，返回 0。
- 否则，返回 high - low + 1。

注意

由于 original 和 bounds 中的数字都是整数，所以 a_i 是整数，L_i 和 R_i 也是整数。因此 x0 必须是整数，且交集区间 [low, high] 中的整数个数可以直接计算。
实际上，代码中直接使用 math.MinInt 和 math.MaxInt 来初始化 low 和 high，但需要注意边界值（因为数字可能很大，但Go的int在64位系统上是64位，足够处理10^9）。

时间复杂度和额外空间复杂度

时间复杂度 ：O(n)。需要遍历数组一次来计算 a_i（实际上可以省略显式存储，在循环中直接计算）和一次遍历所有区间来更新上下界。所以总线性时间。
额外空间复杂度 ：O(1)。只使用了常数个额外变量（如 low, high, 循环索引等），没有使用与 n 成比例的额外空间。

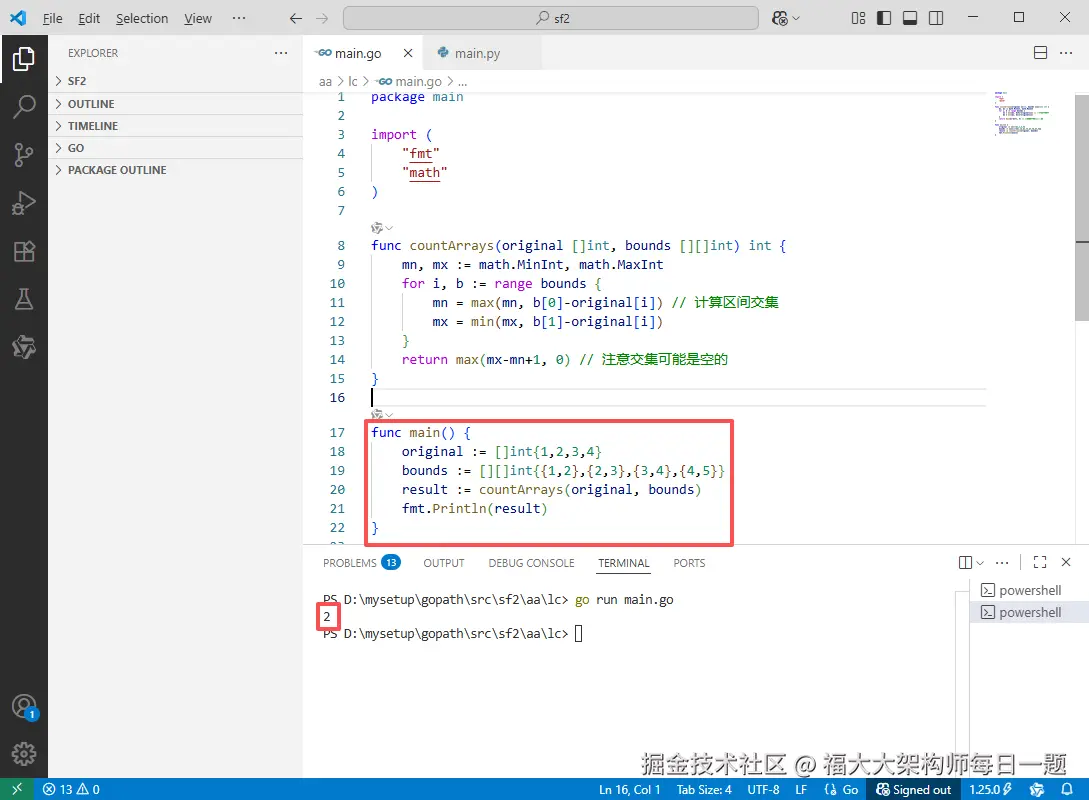
Go完整代码如下：

go 复制代码

package main

import (
	"fmt"
	"math"
)

func countArrays(original []int, bounds [][]int) int {
	mn, mx := math.MinInt, math.MaxInt
	for i, b := range bounds {
		mn = max(mn, b[0]-original[i]) // 计算区间交集
		mx = min(mx, b[1]-original[i])
	}
	return max(mx-mn+1, 0) // 注意交集可能是空的
}

func main() {
	original := []int{1,2,3,4}
	bounds := [][]int{{1,2},{2,3},{3,4},{4,5}}
	result := countArrays(original, bounds)
	fmt.Println(result)
}

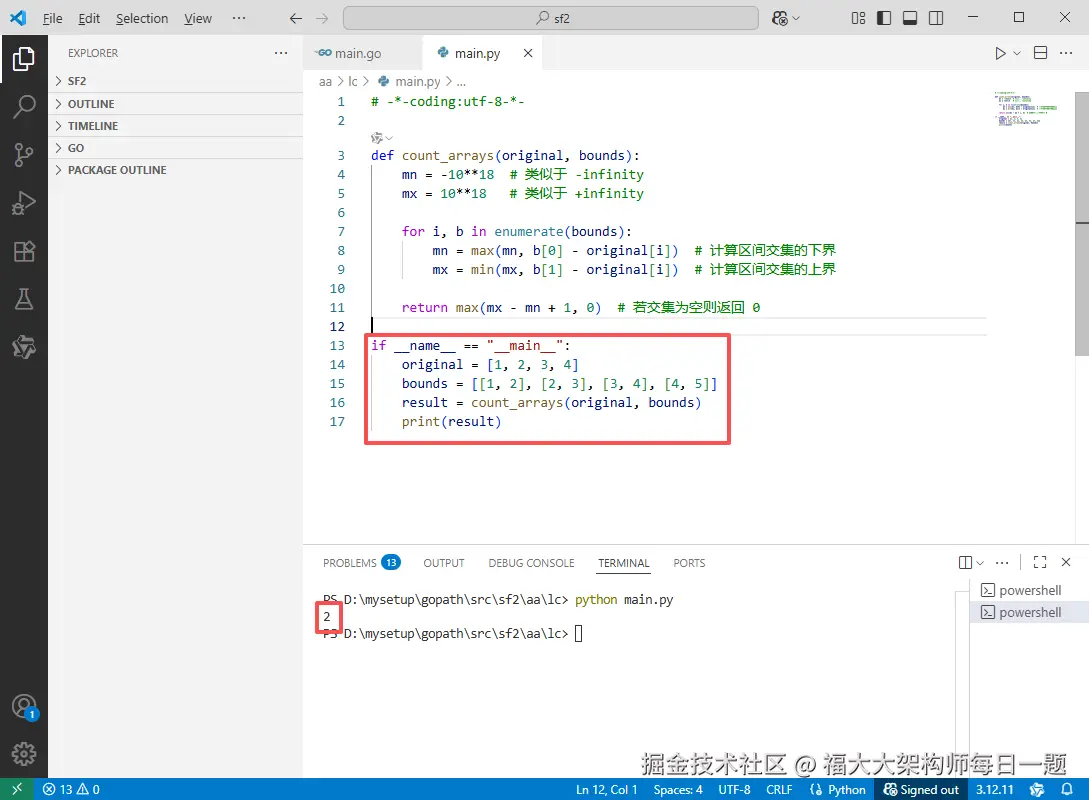
Python完整代码如下：

python 复制代码

# -*-coding:utf-8-*-

def count_arrays(original, bounds):
    mn = -10**18  # 类似于 -infinity
    mx = 10**18   # 类似于 +infinity

    for i, b in enumerate(bounds):
        mn = max(mn, b[0] - original[i])  # 计算区间交集的下界
        mx = min(mx, b[1] - original[i])  # 计算区间交集的上界

    return max(mx - mn + 1, 0)  # 若交集为空则返回 0

if __name__ == "__main__":
    original = [1, 2, 3, 4]
    bounds = [[1, 2], [2, 3], [3, 4], [4, 5]]
    result = count_arrays(original, bounds)
    print(result)