项目地址:https://github.com/hao-ai-lab/FastVideo
模型地址:https://huggingface.co/FastVideo/FastWan2.1-T2V-1.3B-Diffusers/tree/main
发表时间:2025.8.4 (v4版本)

DiTs的扩展能力受限于其二次3D注意力机制,尽管大部分注意力权重集中在少量位置子集上。我们将这一发现转化为VSA,一种可训练且硬件高效的稀疏注意力机制,在训练和推理阶段均可替代全注意力机制。VSA采用轻量级粗粒度阶段将标记池化为区块并识别高权重关键标记;细粒度阶段仅在受块计算布局约束的区块内进行标记级注意力计算,从而确保高效能。这种设计形成单一可微分核,支持端到端训练,无需事后性能分析,且能保持85%的FlashAttention3多流单元(MFU)性能 。我们通过从6000万到14亿参数预训练DiTs,进行了大规模消融实验和扩展规律研究。VSA达到了帕累托最优解,在不降低扩散损失的前提下,将训练所需的浮点运算次数减少了2.53×倍。 对开源Wan-2.1模型进行改造后,注意力计算时间缩短了6×,端到端生成时间从31秒降至18秒,同时保持相近的质量水平。
1 Introduction
注意力计算是视频扩散变换器(DiT)[34,28]扩展时的主要瓶颈。即便是看似简短的5秒720p视频片段,一旦被展平为序列后,也会生成超过10万个token [29,20]。因此,当前最先进的视频DiT模型[20,35,43,26]在使用全分辨率长序列数据训练时,大部分计算资源都耗费在注意力机制上;训练完成的DiT在推理时依然运行缓慢。值得庆幸的是,最新研究[37,47,6,46]揭示了全注意力训练的DiT存在固有稀疏性 :注意力矩阵Softmax中的关键标记(QK⊤/√d)仅对输出产生显著影响,而绝大多数条目接近零值。这种固有稀疏性要求开发专为视频DiT设计的原生、可训练的稀疏注意力机制。
现有研究大多将稀疏性视为预训练DiT的后处理加速手段,而非首要训练基础 。例如Sliding Tile Attention(STA)[47]和Sparge Attention[46],都是先用全注意力训练模型,再在推理阶段用固定或特征导出的稀疏掩码替换每个头 [37,38]。由于稀疏模式是在训练后确定的 ,这些方法既未触及主要训练成本,又导致训练与测试场景不匹配:DiT在密集上下文中学习参数,却在稀疏上下文中进行评估。这种不匹配的上限将密集模型的最佳质量限制在天花板上,实际上,**一旦稀疏度超过温和预算,质量往往会下降。**因此,尽管其成本高得令人望而却步[43,35,20,2,11],最先进的DiTs仍然默认采用二次3d注意力机制。
设计适用于视频深度图(DiTs)的可训练稀疏注意力机制 面临一个根本性的"先有鸡还是先有蛋"的困境:传统方法需要计算完整的注意力矩阵来确定关键标记位置,这不仅会抵消计算效率优势,反而违背了稀疏注意力的设计初衷。反之,若采用廉价的启发式算法而无法精准识别关键标记,则可能遗漏高权重区域,导致效果欠佳。更重要的是,任何实际应用中的注意力实现都必须遵循现代GPU内核(如Flash 注意力机制[FA])所需的块稀疏布局------否则理论上的效率提升将难以转化为实际运行速度的加速。因此,核心研究问题在于:如何在硬件对齐的块结构框架下,准确预测关键标记,同时避免我们试图规避的二次方复杂度代价?
本文提出VSA(视频稀疏注意力机制),这是一种专为视频深度图谱设计的可训练、硬件友好型稀疏注意力框架,其灵感源自近期大型语言模型的研究成果[44,25,30]。该机制采用分层粒度设计,如图1所示:
- 粗粒度阶段首先将包含(4,4,4)个标记的立方体聚合为单一表征,通过立方体间密集注意力计算;
- 由于注意力作用于池化后的短序列,因此具有轻量化特性,同时能预测关键标记所在立方体并建模全局上下文。
- 精粒度阶段则在前K个选定立方体内进行标记级注意力计算。
最终输出通过可微分门控函数整合两阶段结果。
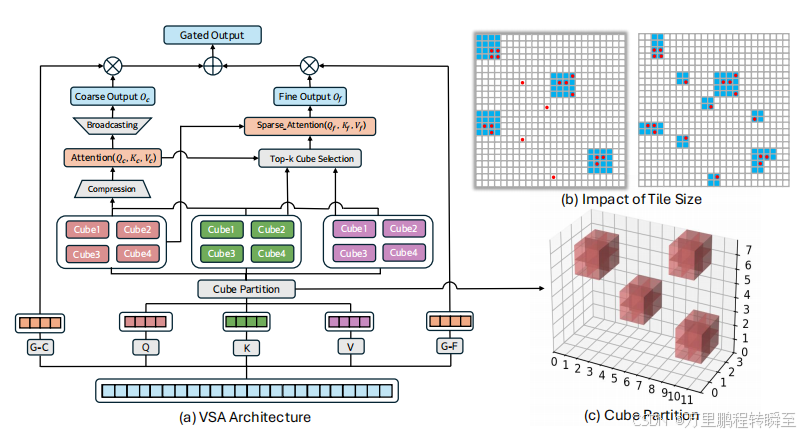
VSA概述。(a) VSA通过引入分层稀疏注意力机制,采用不同粒度(粗粒度与细粒度)进行处理。(b)较大的块尺寸(左图)会模糊注意力模式,而较小的块尺寸则能让粗粒度阶段在接近标记分辨率时定位关键标记。红色圆点标示关键标记。(c)图示(2,2,2)立方体划分方案(实际应用中VSA采用(4,4,4)划分方式)
得益于端到端可训练特性,VSA通过数据学习而非启发式方法识别关键标记。为确保硬件效率,VSA经过精心设计,将时空立方体映射为核级瓦片1 [47],确保同一立方体内的标记加载至同一GPU流处理器,并遵循块稀疏计算布局(§2.2)。
VSA中的一个关键参数是瓦片尺寸。小瓦片能让粗粒度阶段将关键标记定位在接近标记分辨率的位置 ,而细粒度阶段仅关注那些被精确定位的立方体 。这种操作虽然以碎片化工作为代价提升了稀疏性并改善了模型质量,但会降低GPU吞吐量。相反,大瓦片虽然能增强算术运算强度,但细粒度阶段仍需处理整个立方体------即使其中只有少数标记重要,这会导致稀疏性模糊(图1 (b))。另一个关键参数是是否在细粒度阶段注入专用局部或时空模式。我们的系统消融研究表明,有效的VSA配置应结合全局粗粒度阶段与可自由选择的细粒度阶段。我们发现,采用64瓦片尺寸和87.5%注意力稀疏度时,性能可与全注意力机制相媲美,同时保持高效的内核执行 。此外,刻意注入局部性启发式方法被证明是不必要的。通过大规模缩放实验(从6000万到14亿参数,最高达4×10²¹次浮点运算),我们对16K序列长度的视频DiTs进行从头预训练,揭示了一个帕累托前沿:VSA可实现注意力FLOPS近8倍的减少,总训练FLOPS减少2.53倍。
为支持VSA的分层稀疏注意力机制,我们设计了GPU内核原型:粗粒度阶段内核将softmax函数、Top-K选择和块索引融合到单次运算中,而 细粒度阶段则采用基于FA [5]的块稀疏注意力内核。这使得我们的VSA实现保留了FA3[31]模型85%的微分注意力单元(MFU)。我们进一步将VSA集成到当前最先进的开源DiT模型Wan2.1 1.3B [35]中,该模型最初是用全注意力训练的。这种集成使注意力计算时间提速6倍,并将端到端推理延迟从31秒缩短至18秒(1.7倍),在H100平台上表现优异。因此,VSA首次实现了视频DiT模型------在训练和推理过程中,注意力仅占运行时间的20%,且不降低质量。
据我们所知,VSA是首个可训练的稀疏注意力方法,通过总计约9万小时的H200实验验证,其扩展性优于全注意力在DiT中的应用。最后,我们希望通过显式消融关键参数(如块尺寸、关键标记预测、局部先验、稀疏性等),能更精准地探索视频DiT模型中稀疏注意力的扩展潜力。
2 Methods
2.1 Sparse Attention Design Space
现代视频深度注意力机制采用三维全注意力模型,能够捕捉整个视频数据集的关联性。给定形状视频的潜在表示(T,H,W),通过将三维空间中的每个标记位置(t,w,h)映射到一维序列中的位置n(计算公式为n=tHW+hW+w),最终生成长度为L = T HW的一维序列。随后在整个一维序列上应用全注意力机制,使每个标记都能与其他所有标记产生交互。其中Q、K、V∈RL×dQ、K、V∈R^{L×d}Q、K、V∈RL×d分别表示单个注意力头的查询矩阵、键矩阵和值矩阵;M∈−∞,0L×LM∈{−∞,0}^{L×L}M∈−∞,0L×L则是用于指定标记间允许连接关系的注意力掩码。最终计算得到的注意力输出O遵循以下公式:
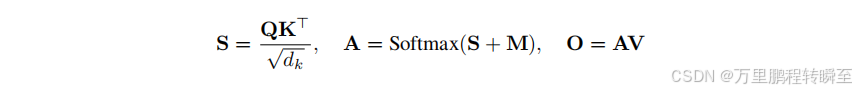
Block Size vs. Hardware Efficiency. 在全注意力机制中,矩阵M的所有元素均为零值。稀疏注意力机制通过引入−∞元素,理论上可减少总浮点运算次数(FLOPS) ,因为无需计算QK⊤QK^⊤QK⊤和AV中的对应元素。然而现代加速器主要针对密集计算进行优化,导致非结构化稀疏性难以有效提升实际性能。块结构稀疏注意力[5]通过将稀疏性与硬件特性相匹配来解决这一问题。该方法将注意力掩码M分割为(Bq,Bk)²大小的块,每个块内的元素保持相同值。这种设计使得GPU上的每个块要么作为密集块处理,要么完全跳过,从而最大化硬件效率。块尺寸B是关键设计参数:较小尺寸的块能实现灵活的细粒度稀疏性,但硬件效率较低;较大尺寸的块虽可提高吞吐量,却限制模型采用更粗略的注意力模式,可能降低建模表达能力(见图1 (b))。因此,选择B值需要在表达力与效率之间进行权衡。实践表明,若能显著提升生成质量,适度降低速度是可以接受的。
Prediction Cost vs. Coverage Quality in Critical Token Selection. 最新研究表明,注意力矩阵A本身具有天然稀疏性[37,47,6,46],其大部分数值接近零值 。这表明,通过构建仅保留矩阵高值区域(即关键标记)的掩码M,我们可以在大幅降低计算成本的同时,实现接近完整的注意力机制。核心设计决策在于确定识别这些关键标记所需的计算量。虽然计算完整注意力分数能获得最精准的选择结果,但这种做法会抵消计算效率的提升------因为只有AV操作能从稀疏性中获益。相比之下**,固定模式(如窗口或时空注意力)虽无需额外预测成本,却容易遗漏重要标记**。受NSA [44]和MoBA [25]的启发,我们提出一种轻量级、可训练的粗粒度注意力模块,无需完全计算A即可估算关键标记的位置。实际应用中的主要挑战在于平衡预测精度与计算效率,以适配DiT架构的需求。
Maintaining Global and Local Context in Sparse Attention. 稀疏注意力机制面临的核心挑战在于其受限的感受野,这会限制模型捕捉全局上下文的能力。为解决这一问题,一种方法是通过引入轻量级全局模块来增强稀疏注意力,从而捕捉粗略的全局信号 。反之,借鉴卷积神经网络等视觉模型中常用的局部先验知识,融入局部上下文信息也能有效提升特征学习效果。我们在第3.1节通过实验消融分析了这两种策略对视频生成质量的影响。
2.2 VSA: Video Sparse Attention
VSA采用基于立方体的分割策略,结合两阶段注意力机制,实现视频潜在数据的高效处理。该方法首先将输入视频潜在数据划分为空间和时间连续的立方体,随后通过粗粒度阶段识别关键区域,并在细粒度阶段对这些区域进行详细的标记级注意力计算。这种设计既保证了计算效率,又保留了捕捉视频数据全局与局部关联的能力。
对于具有形状特征的视频潜在表示(T,H,W),VSA将其分割为多个立方体,每个立方体的形状特征为(Ct,Ch,Cw)(图1 ©)。VSA通过将视频潜在表示中的每个立方体映射到GPU超级矩阵上的单个瓦片(瓦片尺寸B = Ct×Ch×Cw),实现了稀疏注意力算法与核函数实现的协同设计。我们假设视频潜在表示的形状特征(T,H,W)是瓦片尺寸的整数倍,并定义(Nt,Nh,Nw)=T Ct,C H h,C W w。.当将三维视频潜在表示展平为一维序列时,位置为(T,H,W)的每个标记都会被赋予一个一维索引n,其映射关系如下:
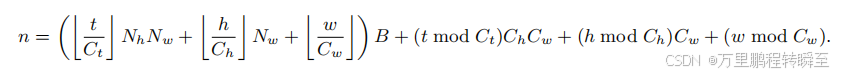
基于这种立方体划分架构,VSA通过两阶段注意力机制实现关键标记位置的高效预测,无需计算完整的注意力矩阵A(如图1 (a)所示)。在粗粒度阶段,我们对每个(Ct,Ch,Cw)立方体进行均值池化处理,生成Qc、Kc、Vc∈RL/B×dQc、Kc、Vc∈R ^{L/B×d}Qc、Kc、Vc∈RL/B×d等立方体级表征。该阶段随后计算注意力得分Ac∈RL/B×B/LAc∈R ^{L/B×B/L}Ac∈RL/B×B/L并输出Oc。注意力掩码M的生成方式是:从Ac中按行选取Top-K个条目并设其余为−∞,再将这些条目广播到L×L大小的全分辨率掩码。由于粗粒度阶段作用于立方体级表征,该掩码自然符合块稀疏结构。当将掩码从B/L×L/B广播到L×L时,Ac中每个选定条目会在M3中扩展为BL×L的块状结构。这种块稀疏模式对硬件效率至关重要------它使下一阶段能以与GPU内存访问模式相匹配的方式处理注意力信息,从而实现高效的并行计算。
接下来,在精细阶段,该掩码M引导Q、K、V∈RL×dQ、K、V∈R^{L×d}Q、K、V∈RL×d的细粒度注意力计算,生成输出Of。最后,两个阶段的输出被合并以获得最终输出O。
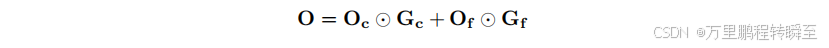
其中Gc和Gf是通过输入隐藏状态的线性投影获得的门控向量。由于粗粒度阶段引入的计算成本可忽略不计(不足总FLOPS运算量的1%),因此整体稀疏性可通过KL/B进行近似计算。但由于采用逐行Top-K选择机制,FlashAttention无法直接应用于粗粒度阶段,导致延迟增加。§2.4节讨论了如何缓解这种开销。附录A提供了VSA的伪代码实现。§3.1和3.2节表明,使用较小的B值能生成更具表现力的稀疏注意力模式并提升性能,但会导致注意力核执行速度变慢。将B设为64且(Ct,Ch,Cw)设为(4,4,4)时,在表达力与效率之间取得了良好平衡。我们进一步证明,将全局上下文的粗粒度阶段与令牌级稀疏注意力的细粒度阶段相结合是必要且充分的------专门用于局部上下文建模的模块仅提供微小增益。当K = 32时,系统在不同序列长度下均能保持强劲性能。VSA默认采用这些超参数设置。
2.3 Sparse Adaptation
VSA旨在从零开始训练视频深度智能跟踪器(DiTs),从而降低训练和推理所需的浮点运算次数。该模型也可适配基于全注意力机制预训练的视频DiTs,但若**直接用VSA替代全注意力会导致训练不稳定。我们推测主要原因有二:一是全注意力检查点中未包含门控投影权重G,且这些权重是随机初始化的;二是VSA与全注意力存在显著差异,引入了粗粒度阶段和细粒度阶段的稀疏化设计。**为此,我们开发了退火策略,使模型能平滑过渡从全注意力到VSA。具体实现中,我们将粗粒度门控Gc的权重初始化为零,并移除细粒度门控Gf(相当于将Gf设为1)。同时通过设置稀疏度K = B/L来初始化稀疏化程度,使VSA在训练初期与全注意力等效。随着训练推进,我们逐步将K降低至目标稀疏度水平。与此同时,Gc会随训练迭代更新,使模型能够学习如何平衡粗粒度与细粒度阶段的贡献权重。
2.4 Kernel Implementation
**VSA需要同时实现前向和后向卷积核。**我们在ThunderKittens [32]框架下开发了块稀疏注意力卷积核用于精细阶段。尽管采用64的较小块尺寸,该卷积核仍实现了超过85%的FA多层卷积单元(MFU)性能(参见第3.4节)。如图1所示的粗粒度阶段,需要对立方体级注意力矩阵进行行级Top-K选择。这一步骤需要显式呈现注意力矩阵,因此无法直接使用FA风格的融合卷积核。
一种可能的解决方案是**修改FA卷积核以集成内嵌的双排序算法来完成Top-K操作,从而避免显式呈现。但这种融合需要侵入式重写卷积核并进行精细调优。**我们转而思考:这种复杂度是否必要?对于VSA而言,粗粒度阶段处理的是(4,4,4)立方体,序列长度缩短64倍×,例如10万标记序列缩减至1500个。在此规模下,显式呈现带来的内存开销微乎其微。从FLOPS计算量来看,粗粒度阶段贡献的注意力计算量不足总计算量的0.2%,且如第3.4节所示,即使精细阶段达到87.5%的稀疏度,其运行时间仍仅占14%。这使得进一步的卷积核融合变得没有必要。尽管如此,我们仍对粗粒度阶段进行优化。我们的块稀疏卷积核使用块索引而非二值掩码。因此,将Top-K掩码转换为索引形式会增加额外开销。为此,*我们将softmax、Top-K选择和掩码转索引转换融合到单一卷积核中。这个融合的内核减少了粗阶段运行时间(§3.4C)。
3 Experiments
3.1 Ablation Studies
我们通过大量预训练实验来消融各类设计参数。实验基于Wan2.1模型架构------这是当前最先进的开源视频深度图模型。除非特别说明,我们使用Vchitect-T2V-Dataverse数据集[10]中的形状为(16,32,32)的视频潜在数据 ,从头开始训练包含1.2亿参数、计算量达4.5×10²⁰次浮点运算的模型。根据文献[15,19]确立的扩展规律,我们确定4.5×10²⁰次浮点运算是计算资源的最佳配置:在固定计算预算下对比不同规模模型时发现,采用全注意力机制且以4.5×10²⁰次浮点运算训练的1.2亿参数模型,其性能优于同等计算预算下的小型模型(6000万参数),而继续增加计算量则收益递减。针对VSA及其变体,我们将选定的KV瓦片数量K设为32,实现约87.5%的注意力稀疏度。详细的实验设置与理论依据详见后文。
Data-Dependent Trainable Sparsity Wins Over Fixed-Patterns. 我们首先探究为何全注意力机制在稀疏替代方案中仍占据主导地位。表1a显示,现有稀疏方法(实验1-4)在计算优化训练预算(4.5×10²⁰次浮点运算)下优于全注意力机制(实验5) ,但当训练规模扩大至4×10²¹次浮点运算时,这种优势反而消失。VSA(实验6)则同时超越了传统固定模式方法和全注意力机制 。为深入分析原因,我们在表1b(b)中重点考察两个关键因素:模式类型与阶段贡献度。通过对比数据依赖型模式与采用(3,3,3)窗口的固定局部模式(标记为"L"),并结合粗阶段输出Oc(标记为"C")与精细阶段输出F(标记为"F")的差异,我们发现:无论是否使用门控残差网络(实验7/8对比实验9/10),数据依赖型模式始终优于固定模式,这充分证明了自适应稀疏性与门控残差机制的固有优势。
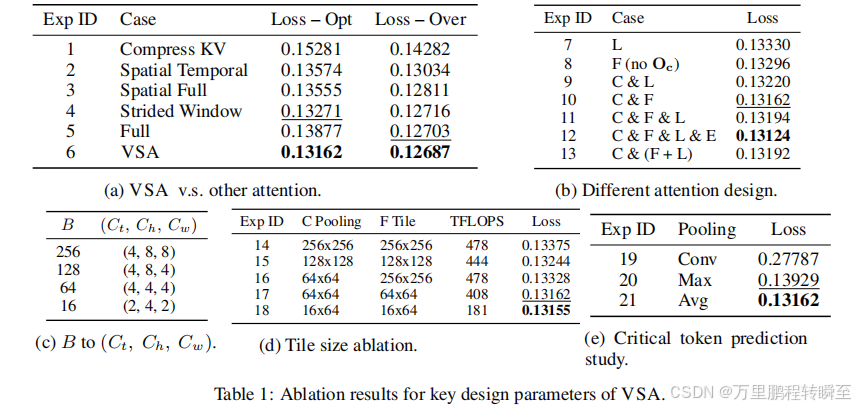
Global Information is Necessary; Locality Priors Offer Limited Gains. 我们测试了三种整合局部上下文的方法:(1)为(3,3,3)窗口注意力机制添加独立的局部处理阶段(实验11);(2)将局部阶段筛选出的立方体明确排除在精细阶段之外(实验12);(3)强制精细阶段包含局部立方体而不设置独立处理阶段(实验13)。这三种变体的表现与更简单的C & F架构相似,表明显式局部建模的增益微乎其微。因此,VSA最终采用了更简洁的C & F架构(实验10),该架构能有效整合全局与局部信息。
Finegrained Attention Map Leads to Better Performance But a Slower Kernel. 如第2.1节分析所示,VSA中的块尺寸B是平衡计算效率与模型性能的关键超参数。它直接影响两个关键方面:(1)通过粗粒度阶段的立方体尺寸能否准确识别关键标记;(2)细粒度阶段注意力机制的粒度。硬件限制部分决定了该参数------英伟达Hopper GPU优化了维度为16倍整数的矩阵乘法运算,较小块尺寸通常会降低算术强度。表1d的基准测试显示,将块尺寸从256×256减小至64×16时,模型FLOPS利用率(MFU)显著下降。
表1c的多尺寸训练实验表明,更小的块尺寸通过更精细的注意力粒度持续降低模型损失。这种改进源于更精细的粒度使粗粒度阶段能更精准预测关键标记立方体,同时让细粒度阶段聚焦于更小、更相关的区域。实验16专门测试了不同粒度阶段间的不匹配情况,证实粗细粒度均显著影响性能。在此实验中,粗粒度阶段采用较小的池化立方体(Ct,Ch,Cw)=(4,4,4)(相当于B = 64),而细粒度阶段则使用较大块尺寸对应(Ct,Ch,Cw)=(4,8,8)(相当于B = 256)。为实现粗粒度阶段预测注意力图与细粒度阶段块稀疏注意力机制的协调,我们在选择前K个条目之前,额外应用了(1,2,2)平均池化操作。综合分析这些结果,我们最终选定64×64的图像块配置(卷积层、通道数、卷积窗口尺寸为4×4×4),作为默认设置。虽然64×16的配置性能略胜一筹,但运行速度却慢了2.26倍(实验18对比实验17),这种权衡显然不划算。
Mean Pooling Is Sufficient. 针对粗粒度阶段,我们还测试了多种池化方式。如表1e所示,平均池化在训练稳定性方面优于最大池化和卷积方法,而后者会导致训练过程出现不稳定现象。
3.2 Scaling Studies
为验证VSA的有效性,我们对一个包含潜在形状(16、32、32)的4.1亿视频latent(16,384个标记)进行了预训练,其规模超过我们现有的1.2亿消融模型。如图2(a)所示,尽管采用87.5%的稀疏度(K=32/256个立方体),VSA仍能实现与全注意力机制几乎相同的损失值,同时将**注意力计算浮点运算量减少8×倍,端到端训练的计算量减少2.53×倍。**进一步从6000万参数扩展至14亿参数的缩放实验(图2(b))证实,VSA始终能生成优于全注意力的帕累托前沿。平行拟合曲线表明,VSA在不同参数规模下均保持2.53×倍的浮点运算量优 势。所有模型均在128块H200 GPU上以最高4××10²¹浮点运算预算进行训练,序列长度为16K。据我们所知,VSA是首个在严格缩放评估中表现优于全注意力的可训练视频深度图稀疏注意力模型。虽然我们计划在更长序列长度下开展全面的缩放研究,但微调后的Wan 2.1模型在23K序列长度时已展现出1.7×倍的推理加速效果(参见第3.3节)。
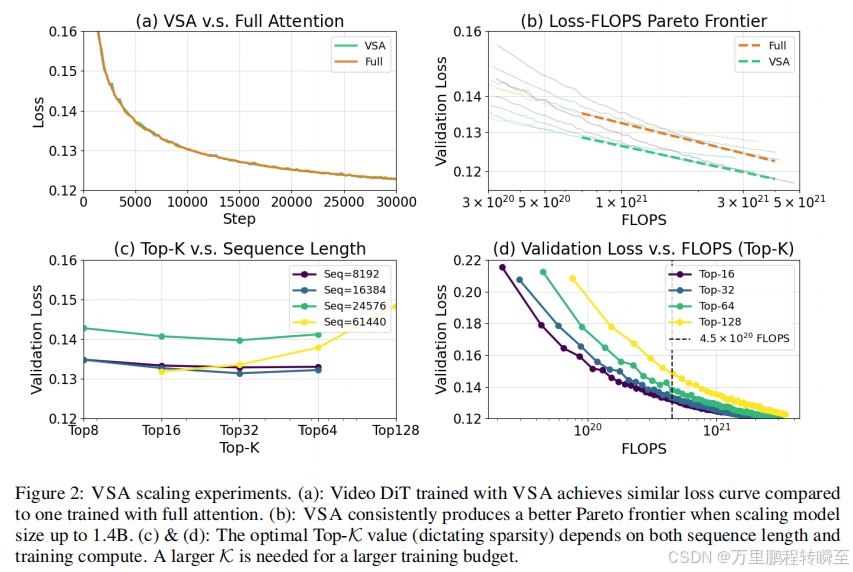
VSA模型设计中的关键问题在于通过Top-K参数确定最佳稀疏度。如图2©所示,我们在固定4.5×10²⁰次浮点运算预算下对1.2亿个模型进行不同序列长度的预训练。令人惊讶的是,在8192、16384和24675三种序列长度下,K = 32始终表现优异,但在61440序列长度时却逊色于K = 16。这与"长序列需要高K值"的传统认知相悖。进一步在61440序列长度下增加计算预算的实验(图2©)表明,当达到1×10²¹次浮点运算时,K = 32最终超越K = 16,其他长度也呈现类似趋势。这些发现表明最优K值取决于序列长度和训练预算。我们推测理想Top-K会随着可用计算资源增加而提升,最终在无限资源时趋近全注意力机制。然而,如何根据预算、模型规模和序列长度精准预测最优K值仍是未解难题。一个有前景的研究方向是将稀疏性作为扩展规律框架[19,15]中的新增维度,与模型规模和总浮点运算量共同考量。引入推理成本后分析更为复杂,因为高K值可能降低训练损失但增加推理开销。我们将深入探讨这些权衡关系留待后续研究。
3.3 Sparse Adaptation
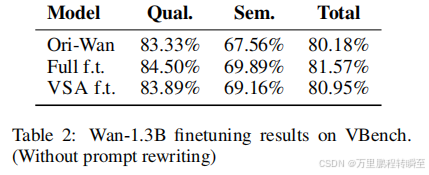
为评估VSA的有效性,我们在Wan-14B生成的合成数据上进一步微调Wan-1.3B模型,该数据采用视频潜在层16×28×52。我们将K值设为32,对应91.2%的注意力稀疏度。如表2所示,VSA在VBench [16]测试中取得的分数甚至高于原始Wan-1.3B。我们推测使用更大模型的合成数据进行训练可能是这一提升的关键因素。为确保公平比较,我们同样使用相同合成数据对Wan-1.3B进行微调。结果显示所有模型在VBench上的表现均相近,表明即使存在显著注意力稀疏度,VSA仍能保持生成质量。我们还将VSA与SVG[37](一种无需训练的注意力稀疏化方法)在极端稀疏度下进行对比。图3显示,尽管VSA具有更高稀疏度,但其表现更优,证明了稀疏注意力训练的有效性。通过VSA训练后,Wan-1.3B的DiT推理时间从31秒(全注意力并使用torch编译器)缩短至18秒。
3.4 Kernel Performance
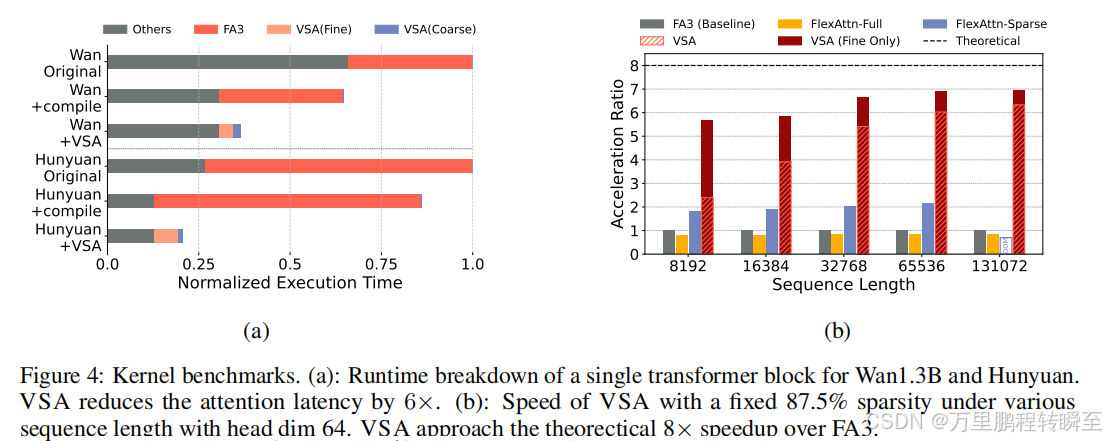
如图4b所示,VSA的细块稀疏核在长序列长度下(相比FlashAttention-3的MFU提升达85%,即近7×倍加速)接近理论极限。即便考虑粗计算阶段,VSA仍能保持超过6×倍的加速效果。相比之下,采用相同块稀疏掩码(64×64块尺寸)的FlexAttention [8]仅实现2×倍加速。将VSA的加速效果应用于Wan-1.3B和Hunyuan模型时,可获得2-3×倍的推理加速,如图4a所示。
3.5 Inspecting VSA
为深入探究VSA的运作机制,我们对微调后的13亿参数模型粗粒度阶段生成的块稀疏注意力图进行分析。如图5(a-f)所示,预测的注意力模式展现出高度动态性,这验证了我们的假设:有效的稀疏注意力机制必须依赖数据特征而非预设结构。即使在同一层内,不同注意力头也常表现出显著差异。许多观察到的模式呼应了经典启发式理论,例如聚焦于查询词附近标记的局部注意力(类似滑动拼图式),或集中于同一帧内标记(d)、同一时间宽度平面(e)或时间高度平面(e)的空间-时间注意力。相反,部分模式偏离简单启发式理论,呈现出高度全局化的特征(b)或局部与全局关注的混合特性©。
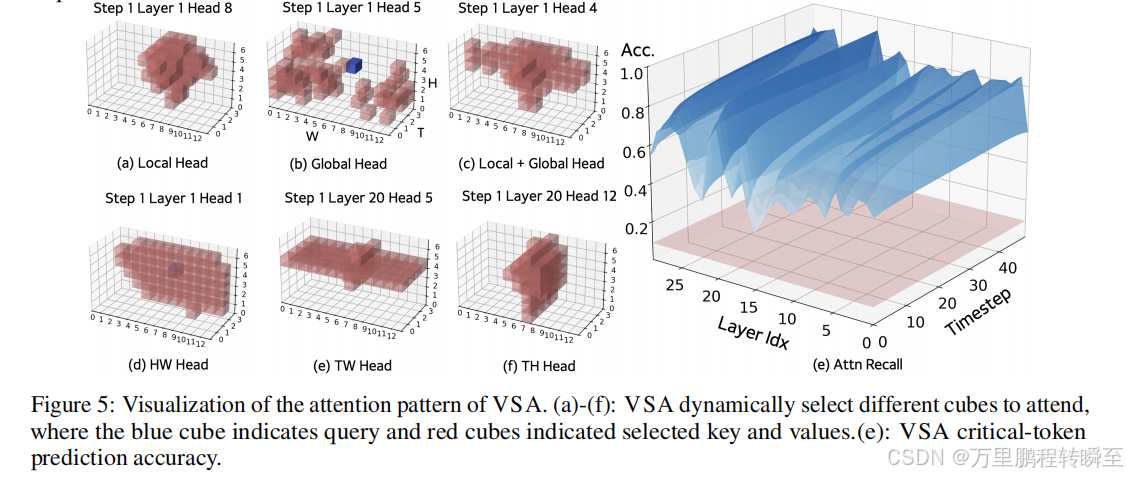
我们通过量化粗粒度阶段筛选出的前32个立方体内的注意力分数总和,来评估关键标记预测的准确率。作为基准,从386个候选立方体中随机选取32个(对应(16,28,52)维度的潜在参数)仅能捕获8%的注意力分数,如图5(e)红色平面所示。与之形成鲜明对比的是,VSA模型始终保持高准确率,在多数层和时间步长中稳定达到至少60%,某些情况下甚至高达90%。这充分证明了VSA在识别关键标记方面具有显著优势。值得注意的是,即使细粒度阶段遗漏了少量注意力权重,粗粒度阶段的直接输出仍能有效弥补这一不足。进一步分析图5(e)发现,预测准确率存在系统性波动:随着时间步长增加,准确率呈现单调上升趋势;但在不同transformer层间,准确率却呈现出曲折变化模式。这种跨层跨步长的动态变化为未来通过自适应Top-K值优化提供了新的思路。
4 Qualitative Examples
我们在图6中定性展示了Wan-1.3B模型的微调过程(第2.3节和第3节)。所有帧均从验证视频中选取特定训练步骤进行采样,其中K = 32。在训练初期,当模型从全注意力机制切换到VSA时,会显现出明显的伪影现象,这反映了注意力结构的变化。随着训练的推进,模型逐渐适应了稀疏注意力机制,并恢复了生成连贯视频的能力。

5 Related Work
LLM中的稀疏注意力机制。在大型语言模型中,固定模式的稀疏注意力机制已得到广泛应用[3,45,1,7,13]。然而实际应用中**,超过90%的FLOP运算量集中在短序列**(≤32K个标记)上,这遵循"训练短、适应长"的范式[40,23,12,42],导致稀疏注意力的应用范围仅限于Mistral [17]等滑动窗口变体。随着LLM模型需要处理超过100万标记的上下文,稀疏注意力机制重新引发关注 。近期研究主要聚焦推理加速[39,48,18,41],而最新方法则探索可训练的动态稀疏模式(如MoBA[25]、NSA [44]),以实现极端长度序列的高效端到端训练。我们从中获得启发,但VSA与MoBA的区别在于:直接将粗粒度注意力输出贡献给最终表征,并采用更小的块结构以适配高效的块稀疏内核。相较于NSA,视频和双向注意力机制的特性避免了注意力模式的分组查询约束。
视频深度注意力机制中的稀疏注意力研究。近期研究探索了在推理阶段对预训练的全注意力深度注意力模型[47,6,46,37,14]进行后处理式稀疏注意力应用。但我们认为,视频深度注意力机制中可训练稀疏注意力的应用场景不仅与语言模型(LLM)存在本质区别,其紧迫性更为突出。首先,视频深度注意力机制需要处理更长的序列数据------例如,仅5秒时长的视频片段就需要10万个上下文标记,使得DiTs的构建成本本质上高于语言模型。其次,与长上下文自适应仅占总训练量一小部分的语言模型不同,当前最先进的视频深度转换模型[20,35,29,33]将大部分计算资源投入全分辨率长序列训练。这导致这些模型在训练和推理阶段都受困于二次方注意力机制。因此,需要采用可训练的稀疏注意力机制(如VSA)作为视频DiTs的核心设计,而非事后补救措施。DSV [33]也尝试在DiT训练中引入注意力机制的稀疏性,但其多阶段架构和基于分析器的设计可能使训练流程复杂化。
6 Limitation and Conclusion
我们提出VSA(可训练稀疏注意力机制),这是一种专为视频深度图(DiTs)扩展而设计的可训练且硬件效率高的稀疏注意力模型。与以往事后应用稀疏性的方法不同,VSA在训练阶段就能联合学习预测和应用注意力稀疏性,同时保持与块稀疏计算布局的兼容性。目前VSA采用固定的立方体尺寸(4×4×4),这要求视频潜在维度必须是4的整数倍。虽然这可能会限制兼容分辨率的选择范围,但实际应用中可以通过生成略大的潜在维度并裁剪至目标形状来解决。另一个开放性问题是确定最佳稀疏度水平。尽管我们的扩展实验(第3.2节)提供了初步见解,但要完全理解其原理可能需要将扩展规律扩展到明确考虑稀疏性、模型规模及训练计算量的层面。在不同模型规模(6000万至14亿参数)和预算(最高4×10²¹次浮点运算)下,我们证明VSA在训练成本降低2.53×的情况下达到全注意力模型性能,并实现FA3模型85%的平均帧利用率。当与Wan2.1-1.3B集成时,端到端延迟可减少1.7×。我们希望本研究能确立可训练稀疏注意力机制作为全注意力模型在视频深度图扩展中的实用且可扩展替代方案。