剑指offer-26、二叉搜索树与双向链表

题⽬描述

输⼊⼀棵⼆叉搜索树，将该⼆叉搜索树转换成⼀个排序的双向链表。要求不能创建任何新的结点，只能调整树中结点指针的指向

思路及解答

递归中序遍历（推荐）

根据二叉搜索树的特点：左结点的值<根结点的值<右结点的值，我们不难发现，使用二叉树的中序遍历出来的数据的数序，就是排序的顺序。因此，首先，确定了二叉搜索树的遍历方法。

我们看下图，我们可以把树分成三个部分：值为10的结点、根结点为6的左子树、根结点为14的右子树。根据排序双向链表的定义，值为10的结点将和它的左子树的最大一个结点链接起来，同时它还将和右子树最小的结点链接起来。

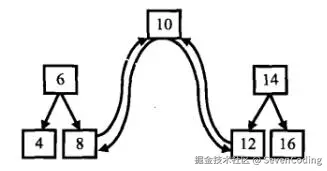
按照中序遍历的顺序，当我们遍历到根结点时，它的左子树已经转换成一个排序好的双向链表了，并且处在链表中最后一个的结点是当前值最大的结点。

具体思路如下，可以利用BST中序遍历的有序性，在遍历过程中调整指针：

中序遍历：按照左子树→根节点→右子树的顺序遍历
指针调整 ：维护一个pre指针记录前驱节点，将当前节点与前驱节点双向连接
头节点处理：第一个被访问的节点（最左节点）作为链表头节点

java 复制代码

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    TreeNode(int x) { val = x; }
}

public class Solution {
    private TreeNode pre = null; // 记录前驱节点
    private TreeNode head = null; // 链表头节点
    
    public TreeNode convert(TreeNode root) {
        if (root == null) return null;
        
        // 中序遍历左子树
        convert(root.left);
        
        // 处理当前节点
        if (pre == null) {
            head = root; // 第一个节点作为头节点
        } else {
            pre.right = root; // 前驱节点的next指向当前节点
            root.left = pre;  // 当前节点的prev指向前驱节点
        }
        pre = root; // 更新前驱节点为当前节点
        
        // 中序遍历右子树
        convert(root.right);
        
        return head;
    }
}

时间复杂度：O(n)，每个节点被访问一次
空间复杂度：O(n)，递归调用栈的空间（最坏情况下树退化为链表）

迭代中序遍历（栈辅助）

使用栈模拟递归过程，避免递归带来的栈溢出风险：

栈辅助遍历：利用栈实现中序遍历的非递归版本
指针调整 ：同样维护pre指针记录前驱节点
头节点标记：使用布尔变量标记第一个节点作为链表头

java 复制代码

public class Solution {
    public TreeNode convert(TreeNode root) {
        if (root == null) return null;
        
        Stack<TreeNode> stack = new Stack<>();
        TreeNode pre = null;
        TreeNode head = null;
        boolean isFirst = true; // 标记第一个节点
        
        while (root != null || !stack.isEmpty()) {
            // 走到最左节点
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            
            root = stack.pop();
            
            if (isFirst) {
                head = root; // 第一个节点作为头节点
                pre = head;
                isFirst = false;
            } else {
                pre.right = root; // 连接前驱和当前节点
                root.left = pre;
                pre = root;
            }
            
            root = root.right; // 处理右子树
        }
        
        return head;
    }
}

时间复杂度：O(n)
空间复杂度：O(n)，栈的空间消耗

Morris遍历

利用Morris遍历实现O(1)空间复杂度的中序遍历：

线索化：利用叶子节点的空指针指向中序前驱或后继
指针调整：在遍历过程中实时调整指针关系
无栈递归：不需要额外栈空间或递归调用

java 复制代码

public class Solution {
    public TreeNode convert(TreeNode root) {
        TreeNode pre = null;
        TreeNode head = null;
        TreeNode current = root;
        
        while (current != null) {
            if (current.left == null) {
                // 处理当前节点
                if (pre == null) {
                    head = current;
                } else {
                    pre.right = current;
                    current.left = pre;
                }
                pre = current;
                
                current = current.right;
            } else {
                // 找到当前节点的中序前驱
                TreeNode predecessor = current.left;
                while (predecessor.right != null && predecessor.right != current) {
                    predecessor = predecessor.right;
                }
                
                if (predecessor.right == null) {
                    predecessor.right = current; // 建立线索
                    current = current.left;
                } else {
                    // 处理当前节点
                    predecessor.right = null;
                    if (pre == null) {
                        head = current;
                    } else {
                        pre.right = current;
                        current.left = pre;
                    }
                    pre = current;
                    
                    current = current.right;
                }
            }
        }
        
        return head;
    }
}

时间复杂度：O(n)
空间复杂度：O(1)，只使用固定数量的指针变量