代码随想录刷题Day47

将有序数组转换为二叉搜索树

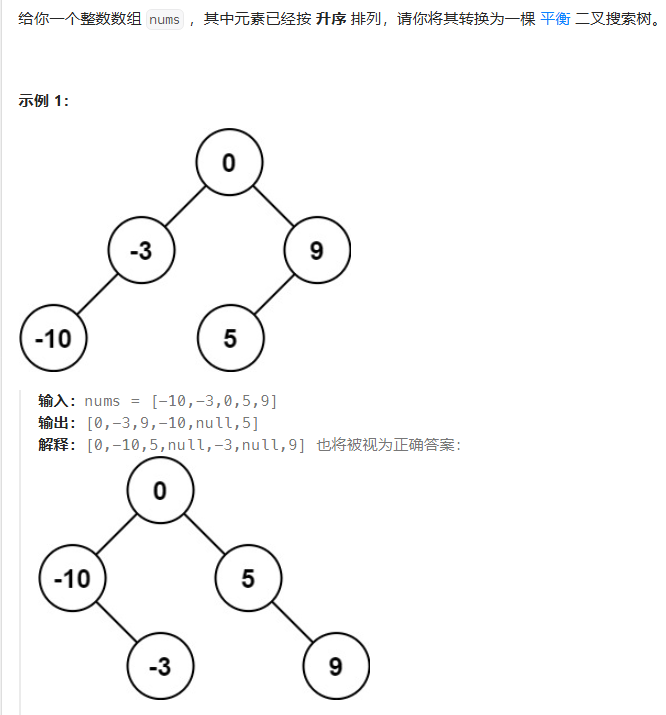
这道题目，看到返回值是构建好的平衡二叉搜索树的指针，很容易可以联想到使用递归的方法。

使用递归方法的关键是，左右子树的递归调用以及对当前根节点的处理。

这道题，

二叉搜索树的特征是左子树节点 < 根节点 < 右子树节点，由于序列是升序的，这个特征自然是可以保证的；

平衡二叉树，要求是左右子树的层数之差不能超过1，为了保证这个条件，可以让序列的中间位置的值作为根节点，这样左右子树就数量大致一样（不一样，也是相差1个节点）。

由此可以给出代码：

cpp 复制代码

class Solution {
public:
    TreeNode* HelpBuildToBST(vector<int> nums,int left,int right){
        if(left > right) return nullptr;
        else if(right == left){
            return new TreeNode(nums[left]);
        }
        else{
            //中间节点为根节点，左右两子树分别是序列的左右两端
            int mid = (right + left)/2;
            return new TreeNode(nums[mid],HelpBuildToBST(nums,left,mid-1),HelpBuildToBST(nums,mid+1,right));
        }
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) {
        int len = nums.size();
        return HelpBuildToBST(nums,0,len-1); 
    }
};

把二叉搜索树转换为累加树

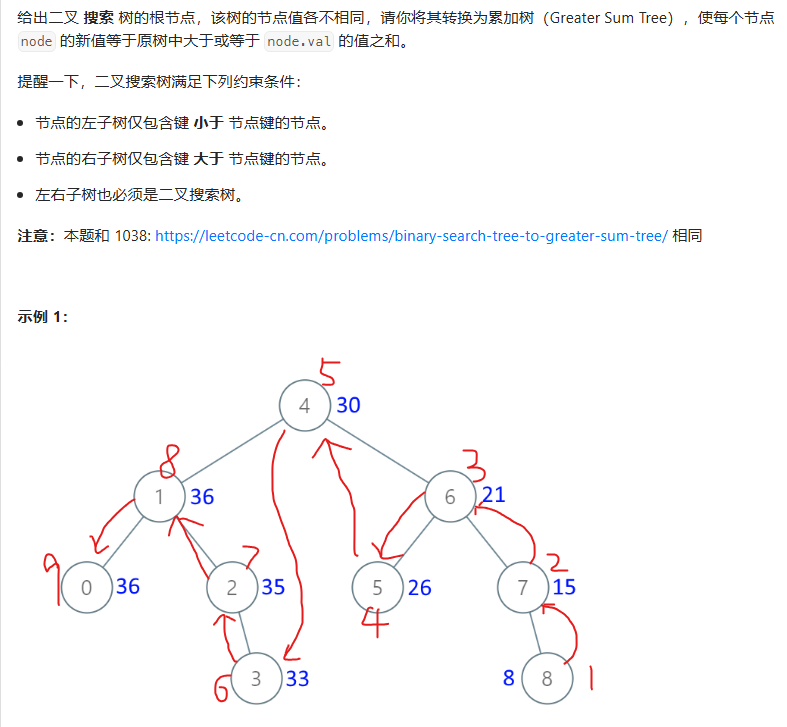
关于这道题目的累加概念的理解，如上图我的标记，处理的顺序是按照右-中-左的遍历顺序来执行的，本质考察的是二叉搜索树的中序遍历，只不过不是左中右，而是右中左了。代码也是中序遍历的代码。我尝试使用递归和迭代的方法做这道题：

迭代法（时间领先100%，内存消耗领先41.25%）：

cpp 复制代码

public:
int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        if(!root) return root;
        else{
            stack<TreeNode*> stackTree;
            stackTree.push(root);
            TreeNode* cur;
            cur = root;
            while(!stackTree.empty()){
                if(cur != nullptr){
                    cur = cur->right;
                    if(cur) stackTree.push(cur);
                }
                else{
                    cur = stackTree.top();stackTree.pop();
                    sum += cur->val;
                    cur->val = sum;
                    cur = cur->left;
                    if(cur) stackTree.push(cur);
                }
            }
            return root;
        }
    }
};

递归法（时间消耗领先100%，内存消耗领先73.89%）：

cpp 复制代码

class Solution {
public:
int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
       if(root==nullptr) return nullptr;
       else{
            if(root->right) root->right = convertBST(root->right);
            sum+= root->val;
            root->val = sum;
            if(root->left) root->left = convertBST(root->left);
            return root;
       }
        
    }
};

这次做的两道题，虽然都和搜索二叉树有关，但核心代码部分，其实没有太大关系。第一个题目主要是平衡二叉树的构建要从中位数开始构建，第二个题目是考察二叉树的中序遍历。