深入浅出链表：从基础概念到核心操作全面解析

小刘鸭地下城2025-09-16 9:57

链表（linked list）是一种线性数据结构，其中的每个元素都是一个节点对象，各个节点通过"引用"相连接。引用记录了下一个节点的内存地址，通过它可以从当前节点访问到下一个节点。

链表的组成单位是节点（node）对象。每个节点都包含两项数据：节点的"值"和指向下一节点的"引用"。

  • 链表的首个节点被称为"头节点"，最后一个节点被称为"尾节点"。
  • 尾节点指向的是"空"

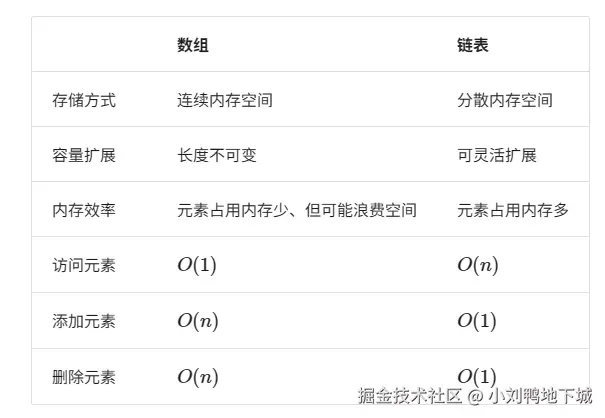
相同数据量下，链表比数组占用更多的内存空间。

学习链表最重要的是 多画图多练习 ：

  • 确定解题的数据结构：单链表、双链表或循环链表等
  • 确定解题思路：如何解决问题
  • 画图实现：画图可以帮助我们发现思维中的漏洞（一些思路不周的情况）
  • 确定边界条件：思考解题中是否有边界问题以及如何解决
JavaScript 复制代码 
/* 链表节点类 */
class ListNode {
    constructor(val, next) {
        this.val = (val === undefined ? 0 : val);       // 节点值
        this.next = (next === undefined ? null : next); // 指向下一节点的引用
    }
}

链表常用操作

初始化链表、插入节点、删除节点、访问节点、查找节点

  • 建立链表分为两步，第一步是初始化各个节点对象，第二步是构建节点之间的引用关系。
  • 只需改变两个节点引用（指针）即可，时间复杂度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( 1 ) O(1) </math>O(1)
  • 在链表中删除节点也非常方便，只需改变一个节点的引用（指针）即可
  • 在链表中访问节点的效率较低。时间复杂度为 <math xmlns="http://www.w3.org/1998/Math/MathML"> O ( n ) O(n) </math>O(n)
JavaScript 复制代码 
/* 初始化链表 1 -> 3 -> 2 -> 5 -> 4 */
// 初始化各个节点
const n0 = new ListNode(1);
const n1 = new ListNode(3);
const n2 = new ListNode(2);
const n3 = new ListNode(5);
const n4 = new ListNode(4);
// 构建节点之间的引用
n0.next = n1;
n1.next = n2;
n2.next = n3;
n3.next = n4;
/* 在链表的节点 n0 之后插入节点 P */
function insert(n0, P) {
    const n1 = n0.next;
    P.next = n1;
    n0.next = P;
}
/* 删除链表的节点 n0 之后的首个节点 */
function remove(n0) {
    if (!n0.next) return;
    // n0 -> P -> n1
    const P = n0.next;
    const n1 = P.next;
    n0.next = n1;
}
/* 访问链表中索引为 index 的节点 */
function access(head, index) {
    for (let i = 0; i < index; i++) {
        if (!head) {
            return null;
        }
        head = head.next;
    }
    return head;
}
/* 在链表中查找值为 target 的首个节点 */
function find(head, target) {
    let index = 0;
    while (head !== null) {
        if (head.val === target) {
            return index;
        }
        head = head.next;
        index += 1;
    }
    return -1;
}

数组 vs 链表

常见链表类型

常见的链表类型包括三种。

  • 单向链表：单向链表的节点包含值和指向下一节点的引用两项数据。我们将首个节点称为头节点，将最后一个节点称为尾节点，尾节点指向空 None 。
  • 环形链表：如果我们令单向链表的尾节点指向头节点（首尾相接），则得到一个环形链表。在环形链表中，任意节点都可以视作头节点。
  • 双向链表：与单向链表相比，双向链表记录了两个方向的引用。双向链表的节点定义同时包含指向后继节点（下一个节点）和前驱节点（上一个节点）的引用（指针）。相较于单向链表，双向链表更具灵活性，可以朝两个方向遍历链表，但相应地也需要占用更多的内存空间。

单链表

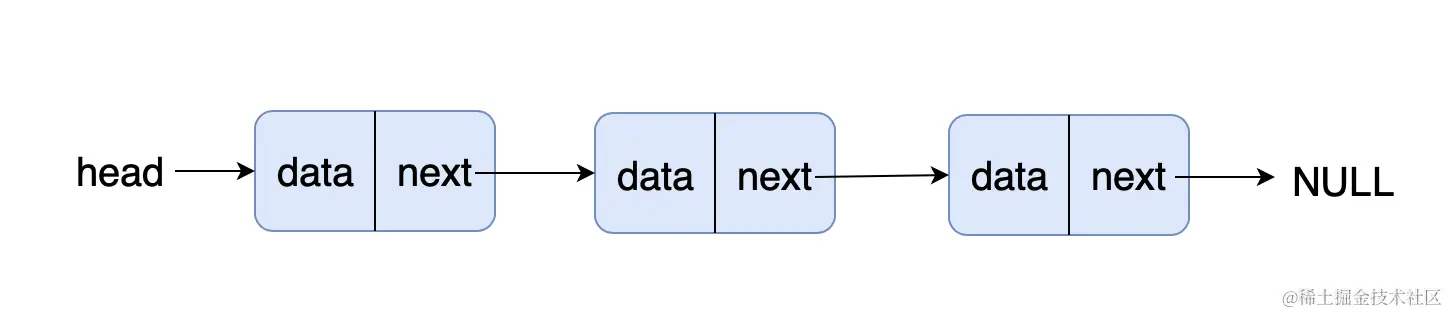
单链表结构：

javascript 复制代码 
function List () {
  // 节点
  let Node = function (element) {
    this.element = element
    this.next = null
  }
  // 初始头节点为 null
  let head = null
  
  // 链表长度
  let length = 0
  // 操作
  this.getList = function() {return head}
  this.search = function(list, element) {}
  this.append = function(element) {}
  this.insert = function(position, element) {}
  this.remove = function(element){}
  this.isEmpty = function(){}
  this.size = function(){}
}

添加节点

初始化一个节点（待追加节点），遍历到链尾，在尾节点后插入该节点

画图实现：

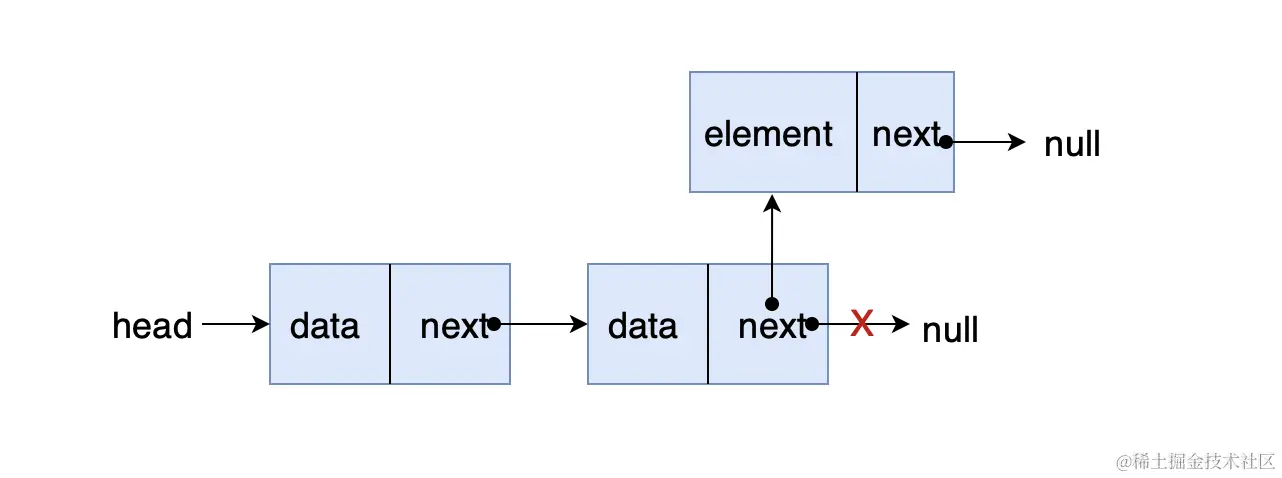
确定边界条件： 当链表为 null ，直接将 head 指向待插入节点，不需要遍历

ini 复制代码 
function append (element) {
  let node = new Node(element),
      p = head
  if (!head){
    head = node
  } else {
    while (p.next) {
      p = p.next
    }
    p.next = node
  }
  length += 1
}

// 测试
let list = new List()
for(let i = 0; i < 5; i+=1) {
  list.append(i)
}

查找节点

确定解题思路： 遍历单链表，判断节点值是否等于待查找值，相等则返回 true ，否则继续遍历下一个节点，直到遍历完整个链表还未找到，则返回 false

确定边界条件： 当链表为 null ，可直接返回 false

java 复制代码 
// 判断链表中是否存在某节点
function search(element) {
  let p = head
  if (!p) return false
  while(p) {
    if (p.element === element) return true
    p = p.next
  }
  return false
}

// 测试
list.search(4) // true
list.search(11) // false

插入节点

初始化一个节点（待插入节点 node ），遍历到 position 前一个位置节点，在该节点后插入 node

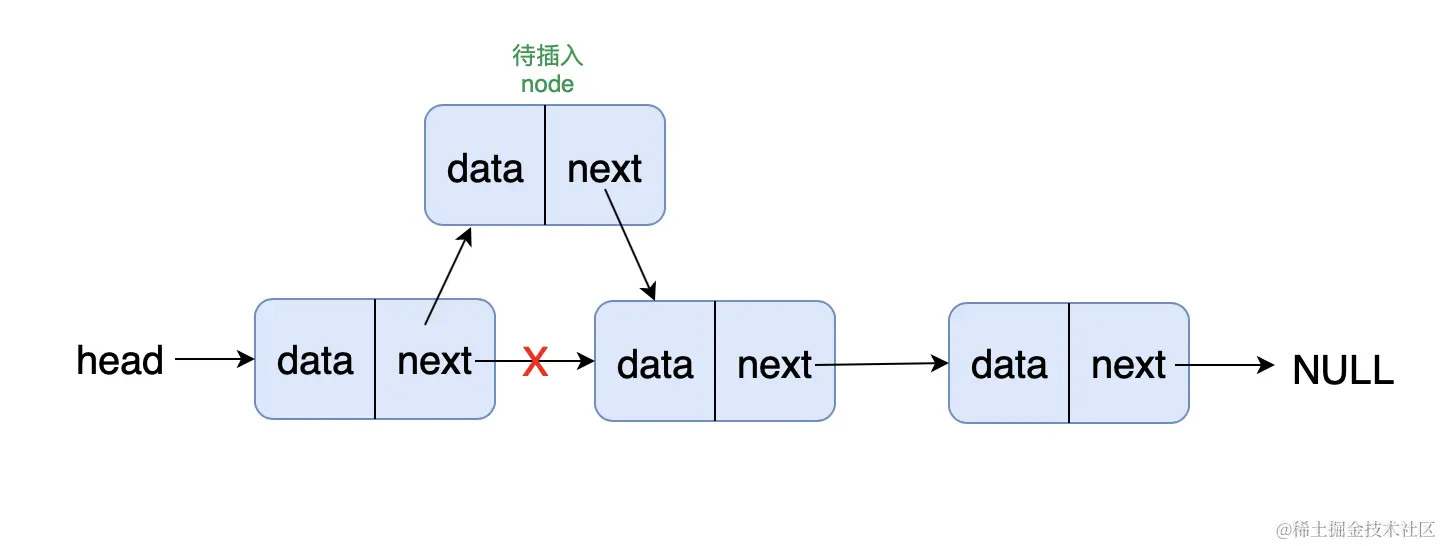
确定边界条件：

  • 当 position 为 0 时，直接将插入节点 node.next 指向 head ， head 指向 node 即可，不需要遍历
  • 当待插入位置 position < 0 或超出链表长度 position > length ，都是有问题的，不可插入，此时直接返回 null ，插入失败
ini 复制代码 
// 插入 position 的后继节点
function insert (position, element) {
  // 创建插入节点
  let node = new createNode(element)
  if (position >= 0 && position <= length) {
    let prev = head, 
        curr = head,
        index = 0
    if(position === 0) {
      node.next = head
      head = node
    } else {
      while(index < position) {
        prev = curr
        curr = curr.next
        index ++
      }
      prev.next = node
      node.next = curr
    }
    length += 1
  } else {
    return null
  }
}

// 测试
list.insert(10)

删除节点

遍历单链表，找到待删除节点，删除

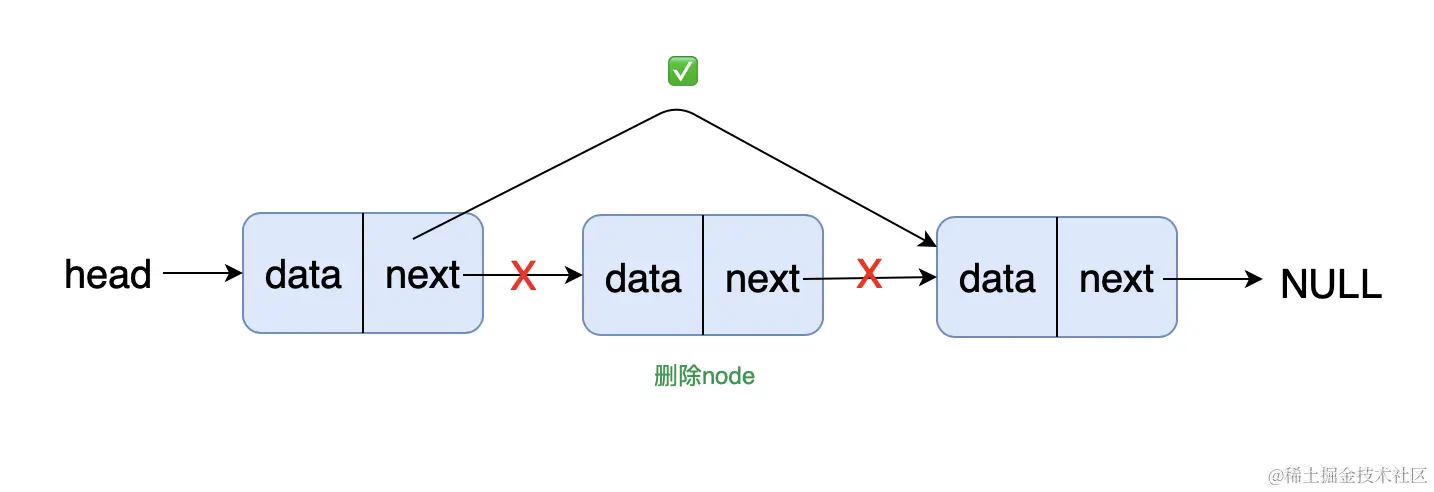
当链表为 null ，直接返回

ini 复制代码 
// 删除值为 element 节点
function remove (element) {
  let p = head, prev = head
  if(!head) return
  while(p) {
    if(p.element === element) {
      p = p.next
      prev.next = p
    } else {
        prev = p
        p = p.next  
    }
  }
}

复杂度分析

查找：从头节点开始查找，时间复杂度为 O(n)

插入或删除：在某一节点后插入或删除一个节点（后继节点）的时间复杂度为 O(1)

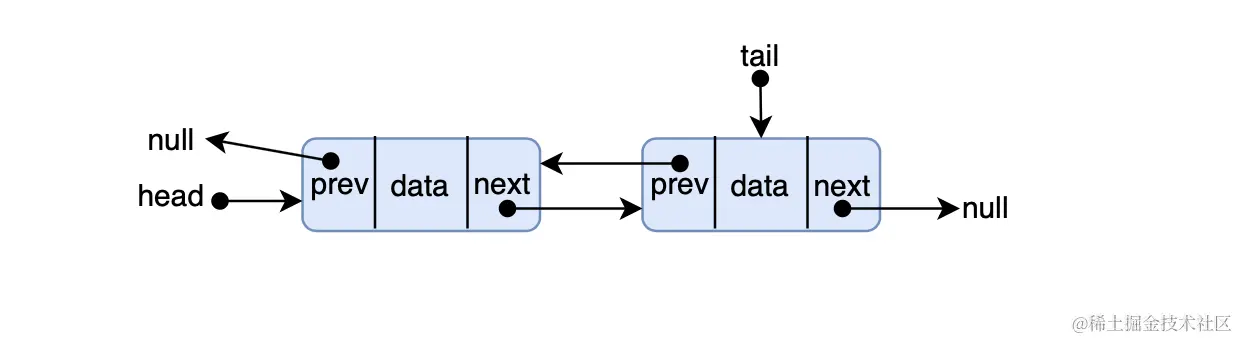
双链表

顾名思义，单链表只有一个方向，从头节点到尾节点，那么双链表就有两个方向，从尾节点到头节点：

javascript 复制代码 
function DoublyLinkedList() {
    let Node = function(element) {
        this.element = element
        // 前驱指针
        this.prev = null
        // 后继指针
        this.next = null
    }
    // 初始头节点为 null
          let head = null
    // 新增尾节点
    let tail = null
  
          // 链表长度
          let length = 0
    // 操作
    this.search = function(element) {}
    this.insert = function(position, element) {}
    this.removeAt = function(position){}
    this.isEmpty = function(){ return length === 0 } 
    this.size = function(){ return length }
}

插入节点

初始化一个节点（待插入节点 node ），遍历链表到 position 前一个位置节点，在该节点位置后插入 node

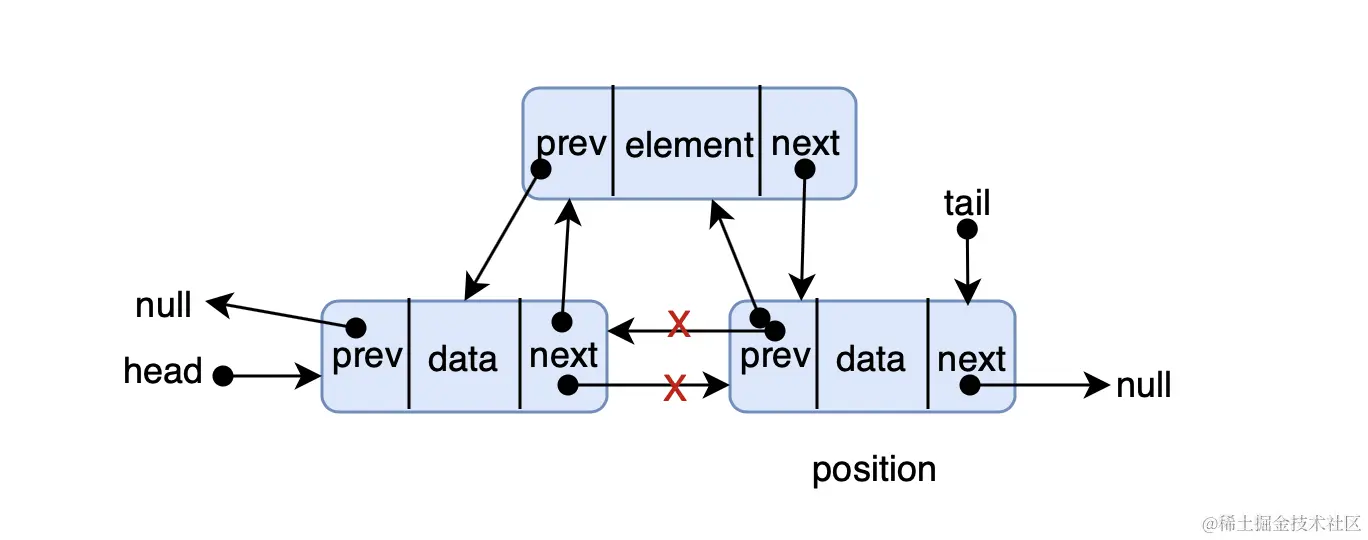
当待插入位置 position < 0 或超出链表长度 position > length ，都是有问题的，不可插入，此时直接返回 null ，插入失败

ini 复制代码 
// 插入 position 的后继节点
function insert (position, element) {
  // 创建插入节点
  let node = new Node(element)
  if (position >= 0 && position < length) {
    let prev = head, 
        curr = head,
        index = 0
    if(position === 0) {
      // 在第一个位置添加
        if(!head) { // 注意这里与单链表不同
          head = node
          tail = node
        } else {
          // 双向
          node.next = head
          head.prev = node
          // head 指向新的头节点
          head = node
        }
    } else if(position === length) {
      // 插入到尾节点
      curr = tial
      curr.next = node
      node.prev = curr
      // tail 指向新的尾节点
      tail = node
    } else {
      while(index < position) {
        prev = curr
        curr = curr.next
        index ++
      }
      // 插入到 prev 后，curr 前
      prev.next = node
      node.next = curr
      curr.prev = node
      node.prev = prev
    }
    length += 1
    return true
  } else {
    return false
  }
}

// 测试
list.insert(10)

删除节点

遍历双链表，找到待删除节点，删除

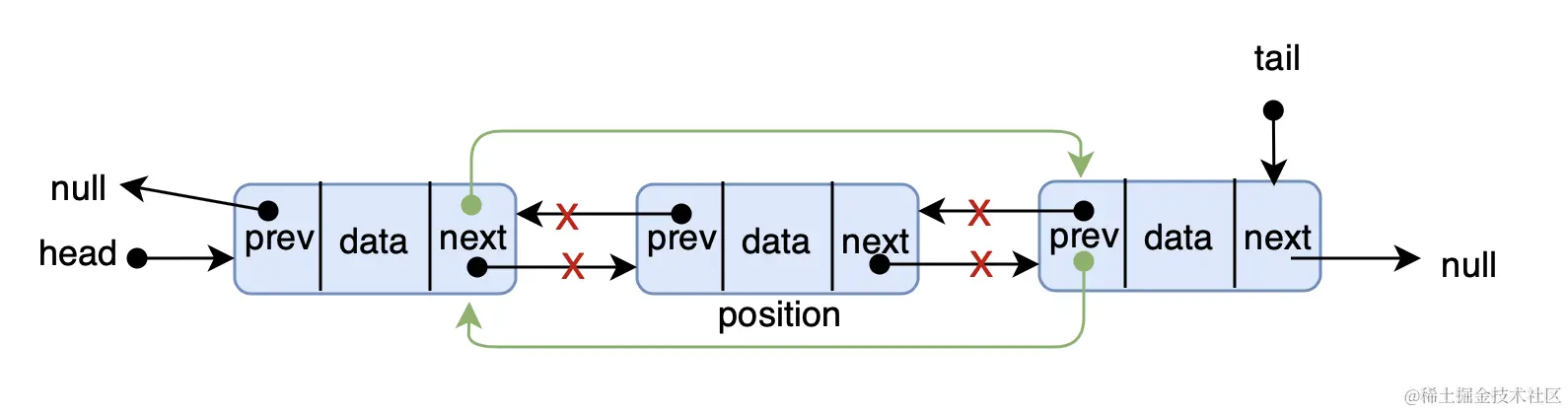
当链表为 null ，直接返回

ini 复制代码 
// 删除 position 位置的节点
function removeAt (position) {
  if (position >= 0 && position < length && length > 0) {
    let prev = head, 
        curr = head,
        index = 0
    if(position === 0) {
      // 移除头节点
        if(length === 1) { // 仅有一个节点
          head = null
          tail = null
        } else {
          head = head.next
          head.prev = null
        }
    } else if(position === length-1) {
      // 移除尾节点
      curr = tial
      tail = curr.prev
      tail.next = null
    } else {
      while(index < position) {
        prev = curr
        curr = curr.next
        index ++
      }
      // 移除curr
      prev.next = curr.next
      curr.next.prev = prev
    }
    length -= 1
    return curr.element
  } else {
    return null
  }
}

查找节点

双链表的查找和单链表类似，都是遍历链表，找到返回 true，找不到返回 false 。

复杂度分析

查找：查找前驱节点或后继节点时间复杂度为 O(1)，其它节点仍为 O(n)

插入或删除：插入或删除前驱节点或后继节点的时间复杂度都为 O(1)

循环单链表

循环单链表是一种特殊的单链表，它和单链表的唯一区别是：单链表的尾节点指向的是 NULL，而循环单链表的尾节点指向的是头节点，这就形成了一个首尾相连的环：

既然有循环单链表，当然也有循环双链表，循环双链表和双链表不同的是：

  • 循环双链表的 tail.next（ tail 的后继指针） 为 null ，循环双链表的 tail.next 为 head
  • 循环双链表的 head.prev（ head 的前驱指针） 为 null ，循环双链表的 head.prev 为 tail

这里以循环单列表为例

javascript 复制代码 
function CircularLinkedList() {
    let Node = function(element) {
        this.element = element
        // 后继指针
        this.next = null
    }
    // 初始头节点为 null
          let head = null
  
          // 链表长度
          let length = 0
    // 操作
    this.search = function(element) {}
    this.insert = function(positon, element) {}
    this.removeAt = function(position){}
    this.isEmpty = function(){ return length === 0 } 
    this.size = function(){ return length }
}

插入节点

初始化一个节点（待插入节点 node ），遍历到 position 前一个位置节点，在该节点后插入 node

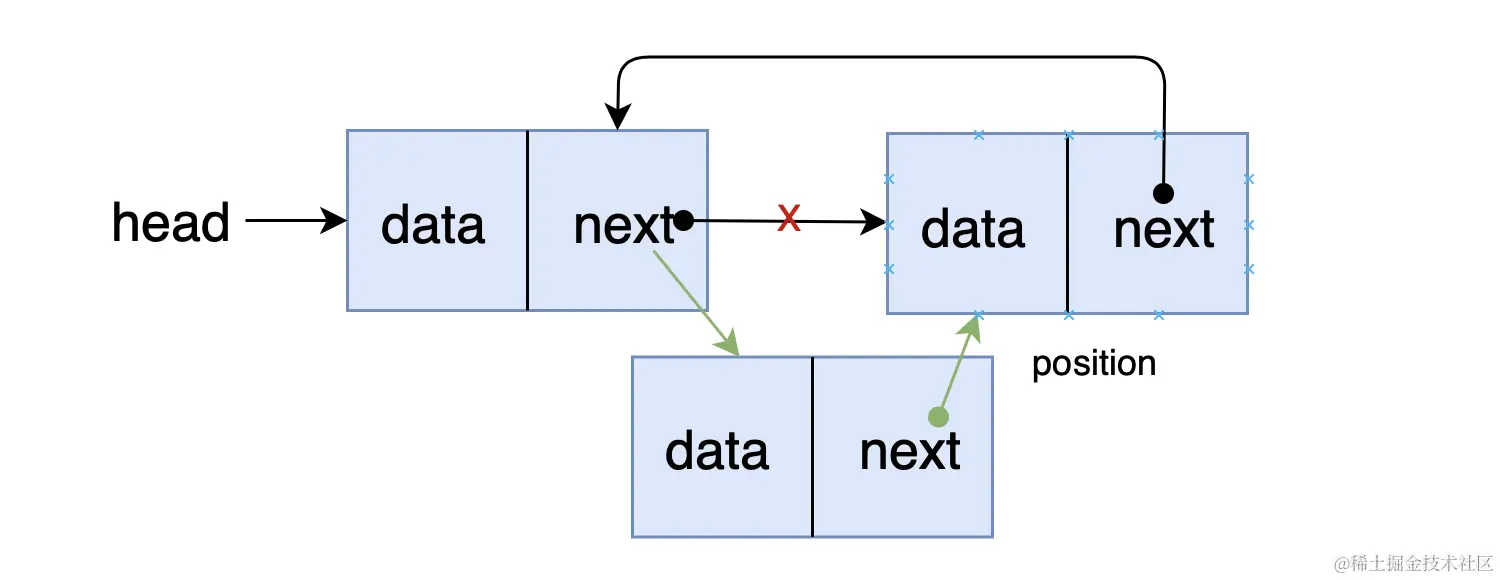
  • 当 position 为 0 时，需要遍历到尾节点，然后在尾节点后插入节点 ， 并将 head 指向
  • 当待插入位置 position < 0 或超出链表长度 position > length ，都是有问题的，不可插入，此时直接返回 null ，插入失败
ini 复制代码 
// 插入 position 的后继节点
function insert (position, element) {
  // 创建插入节点
  let node = new createNode(element)
  if (position >= 0 && position <= length) {
    let prev = head, 
        curr = head,
        index = 0
    if(position === 0) {
      // 与单链表插入不同的
      while(index < length) {
        prev = curr
        curr = curr.next
        index ++
      }
      prev.next = node
      node.next = curr
      head = node
    } else {
      while(index < position) {
        prev = curr
        curr = curr.next
        index ++
      }
      prev.next = node
      node.next = curr
    }
    length += 1
  } else {
    return null
  }
}

// 测试
list.insert(10)

查找节点

和单链表类似，唯一不同的是：循环单链表的循环结束条件为 index++ < length

javascript 复制代码 
// 判断链表中是否存在某节点
function search(element) {
  if (!head) return false
  let p = head, index = 0
  // 和单链表的不同所在
  while(index++ < length) {
    if (p.element === element) return true
    p = p.next
  }
  return false
}

// 测试
list.search(4) // true
list.search(11) // false

删除节点

和单链表类似，唯一不同的是：循环单链表的循环结束条件为 index++ < length

ini 复制代码 
// 删除值为 element 节点
function remove (element) {
  let p = head, prev = head, index = 0
  // 空链表
  if(!head || ) return
  // 仅有一个节点且element一致
  if(length === 1 && head.element === element){  
    head = null
    length-- 
    return  
  }
  while(index++ < length) {
    if(p.element === element) {
      p = p.next
      prev.next = p
      length --
    } else {
        prev = p
        p = p.next  
    }
  }
}

复杂度分析

查找：循环链表从任一节点开始查找目标节点，时间复杂度为 O(n)

插入或删除：它和单链表一样，后继节点插入及删除的时间复杂度为 O(1)

链表典型应用

单向链表通常用于实现栈、队列、哈希表和图等数据结构。

  • 栈与队列：当插入和删除操作都在链表的一端进行时，它表现的特性为先进后出，对应栈；当插入操作在链表的一端进行，删除操作在链表的另一端进行，它表现的特性为先进先出，对应队列。
  • 哈希表：链式地址是解决哈希冲突的主流方案之一，在该方案中，所有冲突的元素都会被放到一个链表中。
  • 图：邻接表是表示图的一种常用方式，其中图的每个顶点都与一个链表相关联，链表中的每个元素都代表与该顶点相连的其他顶点。

双向链表常用于需要快速查找前一个和后一个元素的场景。

  • 高级数据结构：比如在红黑树、B 树中，我们需要访问节点的父节点，这可以通过在节点中保存一个指向父节点的引用来实现，类似于双向链表。
  • 浏览器历史：在网页浏览器中，当用户点击前进或后退按钮时，浏览器需要知道用户访问过的前一个和后一个网页。双向链表的特性使得这种操作变得简单。
  • LRU 算法：在缓存淘汰（LRU）算法中，我们需要快速找到最近最少使用的数据，以及支持快速添加和删除节点。这时候使用双向链表就非常合适。

环形链表常用于需要周期性操作的场景，比如操作系统的资源调度。

  • 时间片轮转调度算法：在操作系统中，时间片轮转调度算法是一种常见的 CPU 调度算法，它需要对一组进程进行循环。每个进程被赋予一个时间片，当时间片用完时，CPU 将切换到下一个进程。这种循环操作可以通过环形链表来实现。
  • 数据缓冲区：在某些数据缓冲区的实现中，也可能会使用环形链表。比如在音频、视频播放器中，数据流可能会被分成多个缓冲块并放入一个环形链表，以便实现无缝播放。

链表面试题

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1输出：true解释：链表中有一个环，其尾部连接到第二个节点。

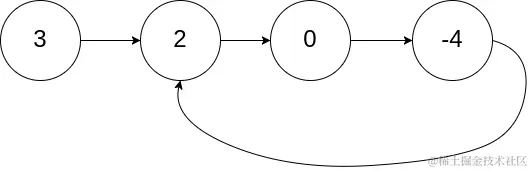
示例 2：

输入：head = [1,2], pos = 0输出：true解释：链表中有一个环，其尾部连接到第一个节点。

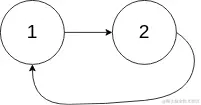
示例 3：

输入：head = [1], pos = -1输出：false解释：链表中没有环。

表记法

给每个已遍历过的节点加标志位，遍历链表，当出现下一个节点已被标志时，则证明单链表有环

bash 复制代码 
let hasCycle = function(head) {
    while(head) {
        if(head.flag) return true
        head.flag = true
        head = head.next
    }
    return false
};

时间复杂度：O(n)

空间复杂度：O(n)

利用 JSON.stringify() 不能 序列化 含有循环引用的结构

javascript 复制代码 
let hasCycle = function(head) {
    try{
        JSON.stringify(head);
        return false;
    }
    catch(err){
        return true;
    }
};

时间复杂度：O(n)

空间复杂度：O(n)

快慢指针（双指针法）

设置快慢两个指针，遍历单链表，快指针一次走两步，慢指针一次走一步，如果单链表中存在环，则快慢指针终会指向同一个节点，否则直到快指针指向 null 时，快慢指针都不可能相遇

vbnet 复制代码 
let hasCycle = function(head) {
    if(!head || !head.next) {
        return false
    }
    let fast = head.next.next, slow = head.next
    while(fast !== slow) {
        if(!fast || !fast.next) return false
        fast = fast.next.next
        slow = slow.next
    }
    return true
};
相关推荐
小刘鸭地下城2 小时前
哈希表核心精要：从 O(1) 原理到链式地址与开放寻址
算法
BenChuat2 小时前
Java常见排序算法实现
java·算法·排序算法
元亓亓亓3 小时前
LeetCode热题100--105. 从前序与中序遍历序列构造二叉树--中等
算法·leetcode·职场和发展
纪元A梦3 小时前
贪心算法在SDN流表优化中的应用
算法·贪心算法
JCBP_3 小时前
QT（4）
开发语言·汇编·c++·qt·算法
码熔burning3 小时前
JVM 垃圾收集算法详解！
jvm·算法
小柴狗4 小时前
C语言关键字详解：static、const、volatile
算法
仙俊红6 小时前
LeetCode每日一题，20250914
算法·leetcode·职场和发展
风中的微尘12 小时前
39.网络流入门
开发语言·网络·c++·算法
热门推荐
01GitHub 镜像站点02UV 工具安装与国内镜像源配置指南03UV安装并设置国内源0446个Nano-banana 精选提示词，持续更新中05A股预测还能更准？开源大模型Kronos带你跑通预测+回测全流程06解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题07KGG转MP3工具|非KGM文件|解密音频08conda中设置镜像地址（附所有可换的地址）09智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践10Claude Code 平替：OpenAI发布 Codex CLI ，GPT-5 国内直接使用