一:算法简介
更快,更不一样的查找方法,相较于传统查找方法,该代码提供了一种在排序的数据中直接通过目标值来找到索引的方法。极大减少了查找速度,以及内存占用。比原有二分查找在数据量大,变化量相对平稳的情况下可快近乎一倍。
二:算法介绍
对于下方图片,我们可以看见,鸟蛋被周围的杂草挡住了,如果鸟没飞到天上找,那么只能在杂草中到处翻杂草,到处走,但是只要飞到天上,鸟蛋在哪,便一清二楚。

算法思想
对于我们的查找算法而言,也是同样的道理,如果我们要找一个数是否存在,我们一般都是遍历索引的方式,来查找该索引对应的值是否为目标值,是的话返回索引,不是返回-1。但是我们不妨换个思路,通过目标值直接来查找索引呢?
对于一个函数来说,y=f(x),知道了y,那么求x便是轻而易举。同样的,在查找算法中,数据的索引是不是可以当作x?数据值是不是可以当作y?知道y,那么求x还会难吗?
不难的。但是对于这些杂乱无章的数据而言怎么找到一个函数来对应每个值和每个索引呢?是不存在这样的函数的。既然不存在,那么上述查找索引的方法是不是就没任何意义了?并不是,没有确切的函数,但是我们有拟合函数(通过数据值,尽量模拟一个形态与数据走向相近的函数)。
通过拟合函数来进行查找的确无法直接通过y找到目标索引x,甚至运算后的索引x还是个小数。那么怎么办?
我们不能找到确定的数,但是我们还找不了索引x具体所在的一个小区间吗?再通过于这个小区间内进行二分查找或其他查找方法来找,不就能找到了吗。想象一个一亿的数据量,但是我们直接通过简单的计算,直接算出了一个大小约为四五万万(线性程度越强,甚至能达到几千)的索引区间,目标值索引就在里头。索引范围直接从一亿降到四五万,在进行二分查找还会慢吗?
没错,对于一组排序好的数据的查找,目标数如果存在,就会位于这组数据的某个区间,该代码提供了一种通过函数来缩小这个区间,最后在这个区间内进行二分查找或其他查找以达到更快速地查询。
名词介绍
误差(△):函数在当x=数据索引时的y值 与 数据值的差
最大误差(△max) : 所有误差(△)当中最大的值
target:查找的目标值
目标区间:经过计算后,target索引所在的区间,也就是最后要查找的区间
leftIndex:在y=f(x)中,target-△max代入y,求出的x值(小数)
left:目标区间的左边界。将leftIndex向下取整
rightIndex:在y=f(x)中,target+△max代入y,求出的x值(小数)
right:目标区间的左边界。将rightIndex向上取整
下面会介绍如何求出以上部分名词(如果以上描述都清楚,那么你大概也知道算法如何实现了。)
三:具体实现流程
先通过下面的图进行理解,下图中(绘画技术实在有限,凑合看吧),黑色高度代表数据值,绿色线代表拟合函数,拟合函数与数据值的距离为△(图中已标出)target目标值为蓝色的垂直线,紫色线为△max大小。红色垂直线为根据拟合函数y=f(x),将target±△max代入y得到的x所在位置,即left与right。
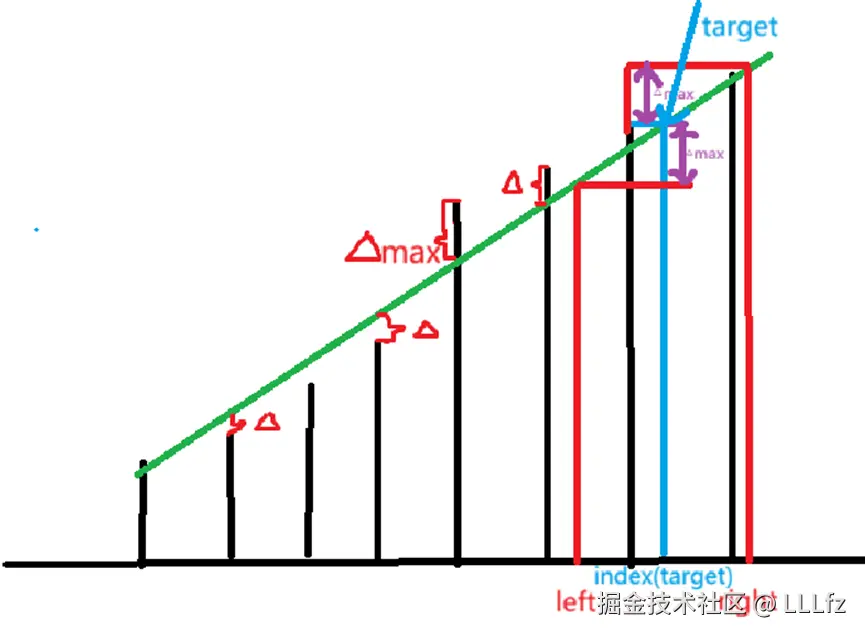
该算法最终要达到的目的就是把查询范围缩小,该图中的[left,right]就是最终要实现的目标。
通过该图可以看出该算法的原理,要查找的值target为蓝线与绿线的交点y值,通过target±△max,并通过函数计算出target±△max的x,target-△max的x为left边界,反之,target+△max的x为right边界。
下面为算法具体步骤。
首先,得找出一个尽量拟合数据的函数,对于数据起伏不是特别大,建议使用线性函数y=kx+b来进行拟合,如线性最小二乘法,极小极大线性拟合算法(推荐) ,拟合函数得尽可能地使△max达到最小,因为△max影响目标区间地大小,进而影响查询效率。找出该拟合函数的斜率k,和b,由于本文不是针对函数拟合算法,所以对如何找出拟合函数不做过多赘述。
其次,我们需要计算出△max。对于拟合函数,某数据的索引为x,该索引在函数中对应的y ,减去该数据值,记为△,找出所有数据索引的△,并标记最大的为△max。
为什么要取△max,试想我们的target在函数的某个位置,目标区间是通过target±△max在函数上对应的x,而target在函数上对应的索引可能比target真实的索引大得多,也可能小得多,如果△过小,没有达到△max,当查找的target的△为△max,那么我们便无法把target真实索引包含在最终区间内,最终查找也就无法找到该target,导致出错。可以举一个极值的例子,有一简单拟合函数y=x,有数据{1 , 1.6 , 2.9 , 4.0 , 5 , 6.3}可得△max为0.4。当要查询数据1.6时,要知道,数据1.6的索引为2,然后通过函数计算得到目标区间范围为[f^-1(y-△max),f^-1(y+△max)]=[1.2,2],target索引就在边界,由此可见,△不取max,如果取偏小的0.3,目标区间就缩小为[1.3,1.9],无法把索引2包含在内,最终查询也就查不到,只有把每个数据的△都考虑到,才能确保所有数据索引都能被包含在目标区间内。
得到拟合函数的k,b,△max即可实现算法。在算法中,我们通过所要查找的数据(记作target),用公式 x=(y-b)/k来计算出target±△max所对应的索引,因此,可以确定最终区为 [leftIndex=(y-△max-b)/k,rightIndex=y+△max-b)/k],但是这个区间边界left和right通过计算后,显而易见并不是整形,而查找(如二分查找)时,我们最后确定的区间范围得是整形,如[1,5],才能通过二分法找到target。怎么办呢?这里不用Math的ceil,floor算法,取而代之的是直接强转为int,double强转为int直接就保留整数,小数点后便被舍弃了,因此,我们的最终区间可以表示为left=(int)leftIndex,right=(int)rightIndex+1 leftIndex和rightIndex在上面区间内已定义。这样,就能表示一个整形边界的区间了。
四:算法具体实现代码(java示例)
了解具体的算法流程后,接下来就是代码实现。再次说明,本文重点在查找,而不在计算拟合函数,所以仅会给出查找算法。拟合函数推荐极小极大线性拟合算法计算。对于详细的数据生成代码,拟合函数计算算法,可以在后续给出的我的gitHub仓库或Csdn项目网址中,下载源码查看。
public
double k, double b, int[] arr, int length) {
//确定目标区间[left,right]
double leftIndex = (target - maxError - b) / k;
double rightIndex = (target + maxError - b) / k;
int left = leftIndex < 0 ? 0 : (int) leftIndex;
int right = rightIndex > length ? length : (int) rightIndex + 1;
//在目标区间进行二分查找
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}(注:参数maxError为△max,target为目标值,k,b为拟合函数的斜率和截距,arr为数据所在数组,length为数组长度(可直接在方法内用arr.length代替)
方法解析:leftIndex和rightIndex为target±△max后通过拟合函数,代入y得到的x值。
left和right为leftIndex和rightIndex向下和向上取整的值,取完整数才能进行二分查找。
left和right确定后直接进行二分查找来查找到target。
查找到返回目标索引,反之返回-1。
五:算法测试(java + C++示例(C++因数据文件原因,仅于1亿测试组测试))
下面,会给出不同数据量大小的数据以及不同查找算法,来进行比较分析(其他算法为AI生成,可能与真实算法有点误差,且数据模型有可能不适合这些算法,测试的数据仅供参考)
所有数据都会在20%和%35,%70阶段改变最大增长值以尽可能让数据不完全线性,以达到更好的实验效果
for
int increment = random.nextInt(maxIncrement - minIncrement + 1) + minIncrement;
currentValue += increment;
yList.add(currentValue);
if(count>interval1){
//此处maxIncrement可根据需求更改
maxIncrement=6;
}
if(count>interval2){
//此处maxIncrement可根据需求更改
maxIncrement=30;
}
if(count>interval3){
//此处maxIncrement可根据需求更改
maxIncrement=20;
}
}目标数据随机生成:
for
targets[i] = random.nextInt(0, intArray[length-1]);
}所有算法都会通过以下代码来计时:
startTime
// 执行函数查找
search();
// 记录结束时间(纳秒)
endTime = System.nanoTime();
// 计算执行时间(纳秒)
durationNanos = endTime - startTime;
// 转换为毫秒
durationMillis = durationNanos / 1_000_000.0;其他算法具体代码
下面先进行参与这次比赛的选手(算法)介绍:
最经典的二分查找
public
int left = 0;
int right = length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}插值查找
public
int left = 0;
int right = arr.length - 1;
while (left <= right && target >= arr[left] && target <= arr[right]) {
int mid = left + (target - arr[left]) * (right - left) / (arr[right] - arr[left]);
if (mid < left || mid > right) {
mid = left + (right - left) / 2; // 退化为标准二分
}
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return (arr[left] == target) ? left : -1;
}块索引优化查找
public
for (int i = 0; i < blockCount; i++) {
blockStart[i] = i * blockSize;
int end = Math.min((i + 1) * blockSize - 1, arr.length - 1);
blockMax[i] = arr[end];
}
int blockLeft = 0;
int blockRight = blockCount - 1;
int targetBlock = -1;
while (blockLeft <= blockRight) {
int blockMid = blockLeft + (blockRight - blockLeft) / 2;
if (blockMax[blockMid] >= target) {
targetBlock = blockMid;
blockRight = blockMid - 1;
} else {
blockLeft = blockMid + 1;
}
}
if (targetBlock == -1) return -1;
int left = blockStart[targetBlock];
int right = Math.min((targetBlock + 1) * blockSize - 1, arr.length - 1);
return binarySearchInRange(arr, target, left, right);
}哈希缓存查找
public
if (cache.containsKey(target)) {
int cachedIndex = cache.get(target);
if (cachedIndex >= 0 && cachedIndex < arr.length && arr[cachedIndex] == target) {
return cachedIndex;
}
cache.remove(target);
}
int index = binarySearch(arr, target);
if (index != -1) {
cache.put(target, index); // 存入缓存
}
return index;
}测试结果:
1.数据量100 000 000 查找量1 000 000
两次测试:
java:
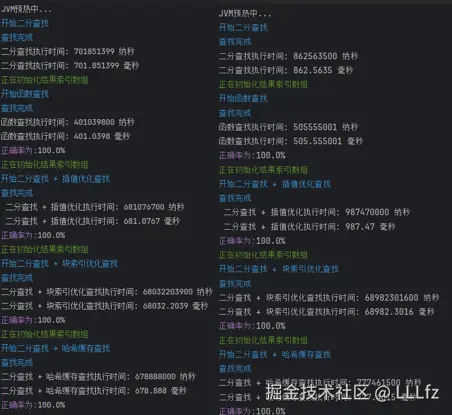
C++:块索引查找时间查找过长,无意义,直接略过
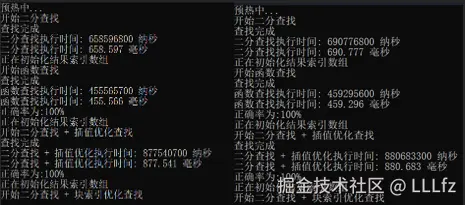
2.数据量10 000 000 查找量1 0 0000
两次测试:
3.数据量100 000 查找量10 000
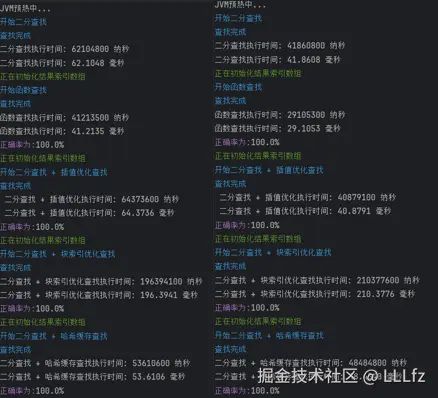
两次测试:
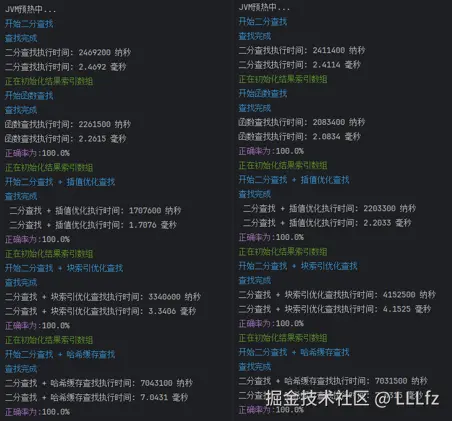
4.数据量1 000 查找量1 000
两次测试:
测试总结
由本次实验可以看出,在数据量庞大的时候(100 000 000),该算法的速度较其他方法更快,甚至快出了近一倍。但是当数据量来到(100 000)时,速度已接近于二分法,数据量更小时,会慢于二分法,但相较于块索引和哈希查找,相对来说还是更快。
所以,本算法对于数据量庞大,数据增长较为平缓的数据来说,其查找效率尤其的快,远胜其他算法。
六:数据增加/减少
一:添加数据
本算法对于数据组的插入更新并不友好,较适合删改较少的静态数组。如果有数据的插入导致△max发生改变(新数据的△>△max),而不重新更新拟合算法,那么会导致目标区间"盲目增大",因为这个拟合函数可能并不适合该新数据。
下面提供一种方案:
在插入数据时,可以判断数据插入,新数据的值的△,如果△<△max,那么直接插入,没有任何影响,如果△>△max,那么仅更新△max并继续用该拟合算法,然后设置个定时器或者其他方案,每隔一段时间,或者△max变化的次数达到一定值时,重新计算拟合算法(计算拟合算法在1亿的数据量下计算一次其实也才7-8秒,相较于其快速查找所省下来的时间微乎其微)。另外,如果数据并不需要即刻插入,那么可以在插入前,用新数据的索引代入拟合函数并计算出△,如果△<△max,则直接插入,如果△>△max,那么将其插入队列,等队列中数量达到一定值,或者设置时间截至,再把数据全部一次性插入,然后更新拟合函数。
二:数据删除
数据删除较为友好,如果删除的数据刚好是△max的数据,那么删除后仅需更新△max即可,如果较多的数据删除,那么请隔一段时间重新计算一次拟合函数,以使算法保持鲜活。
上述添加/删除方案未经实际验证,仅理论上成立。
七:总结:
经过以上讨论,我们可以看出在数据庞大且线性相关较强的数据中查找时,该算法相较于其他算法尤其迅速。但是当数据量小,数据变化很大时,该算法会稍次于二分查找。所以在选择查找算法时,评价一下自己的数据模型,根据数据模型来选择适合自己的查找算法。 如果对于以上内容。有任何疑问皆可在评论给出。
八:测试代码分享
该算法代码:
Github:github.com/bingpiano/f...
GitCode:gitcode.com/2301_819248...