目录
[2.size 与 empty](#2.size 与 empty)
[3.begin 与 end](#3.begin 与 end)
[4.push_back 与 pop_back](#4.push_back 与 pop_back)
[5.front 与 back](#5.front 与 back)
[5.洛谷(UVA)---The Blocks Problem](#5.洛谷(UVA)---The Blocks Problem)
一.vector使用介绍
vector是c++ stl 库提供的一种动态顺序表容器,创建以及增删改查等逻辑已经实现完毕,被放在了类当中
1.数组创建与初始化
- vector<int> a1 //创建了一个空的可变长数组,里面为int型数据
- vector<int> a2(10) //数组初始化,长度为10,默认值为0
- vector<int> a3(10,2) //数组初始化,长度为10,默认值为2
- vector<int> a4 = {1,2,3,4,5} //初始化列表的创建方式
<> 里面可以存放任意类型的数据类型,结构体类型、string类型......
二维数组的初始化:vector<vector<int>> a7(10,vector<int>(10)) //创建一个10行10列的二维数组,一个括号都不能省略
二维数组的特殊初始化:vector<int> a8[N] //创建一个 N 大小的vector类型数组,数组是vector类型的,说明是一个行为 N 列未确定的二维数组
2.size 与 empty
size:返回元素实际个数
empty:返回顺序表是否为空,是一个 bool 类型的返回值**(为空 -> t ,不为空 -> f)**
时间复杂度:O(1)
3.begin 与 end
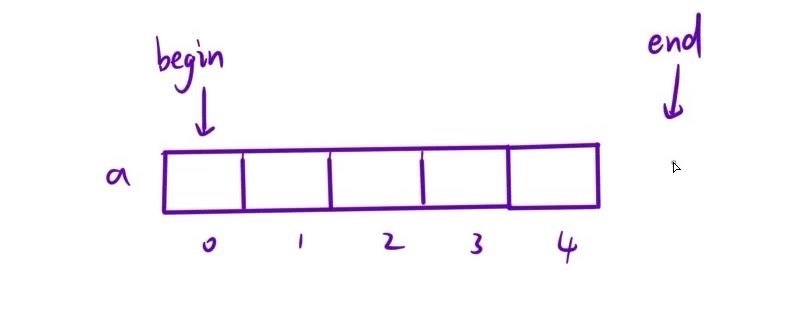
1.begin :返回起始位置的迭代器(左闭)
2.end :返回终止位置的下一个位置的迭代器(右开)
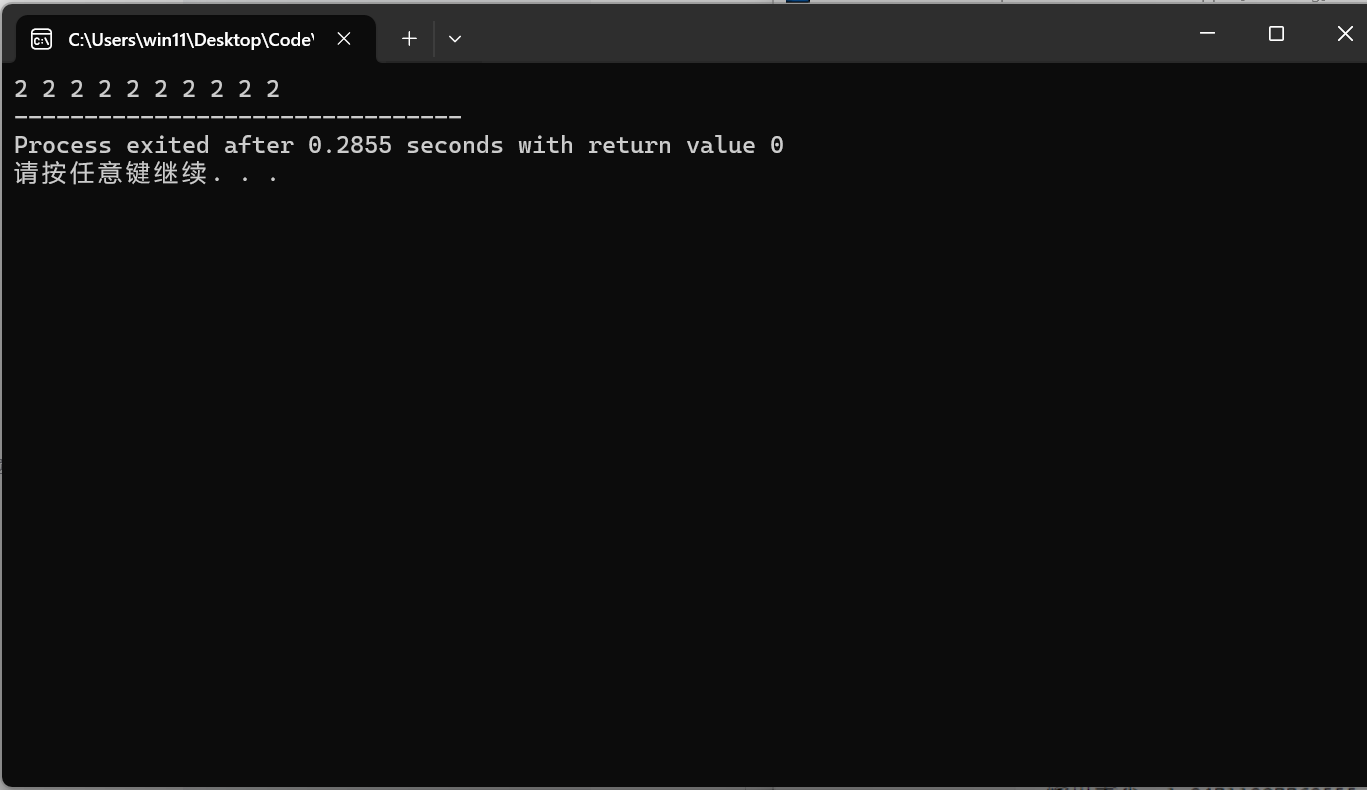
代码演示:
cpp
#include<iostream>
#include<vector>
using namespace std;
int main()
{
vector<int> a(10,2);
for(vector<int>::iterator it = a.begin();it != a.end();it++)
{
cout<<(*it)<<" ";
}
return 0;
}
4.push_back 与 pop_back
1.push_back:尾部添加一个元素
2.pop_back:尾部删除一个元素
当然还有 insert(插入)与 erase(指定删除),不过时间复杂度比较高,尽量不使用
时间复杂度:O(1)
5.front 与 back
1.front:返回首元素
2.back:返回尾元素
时间复杂度:O(1)
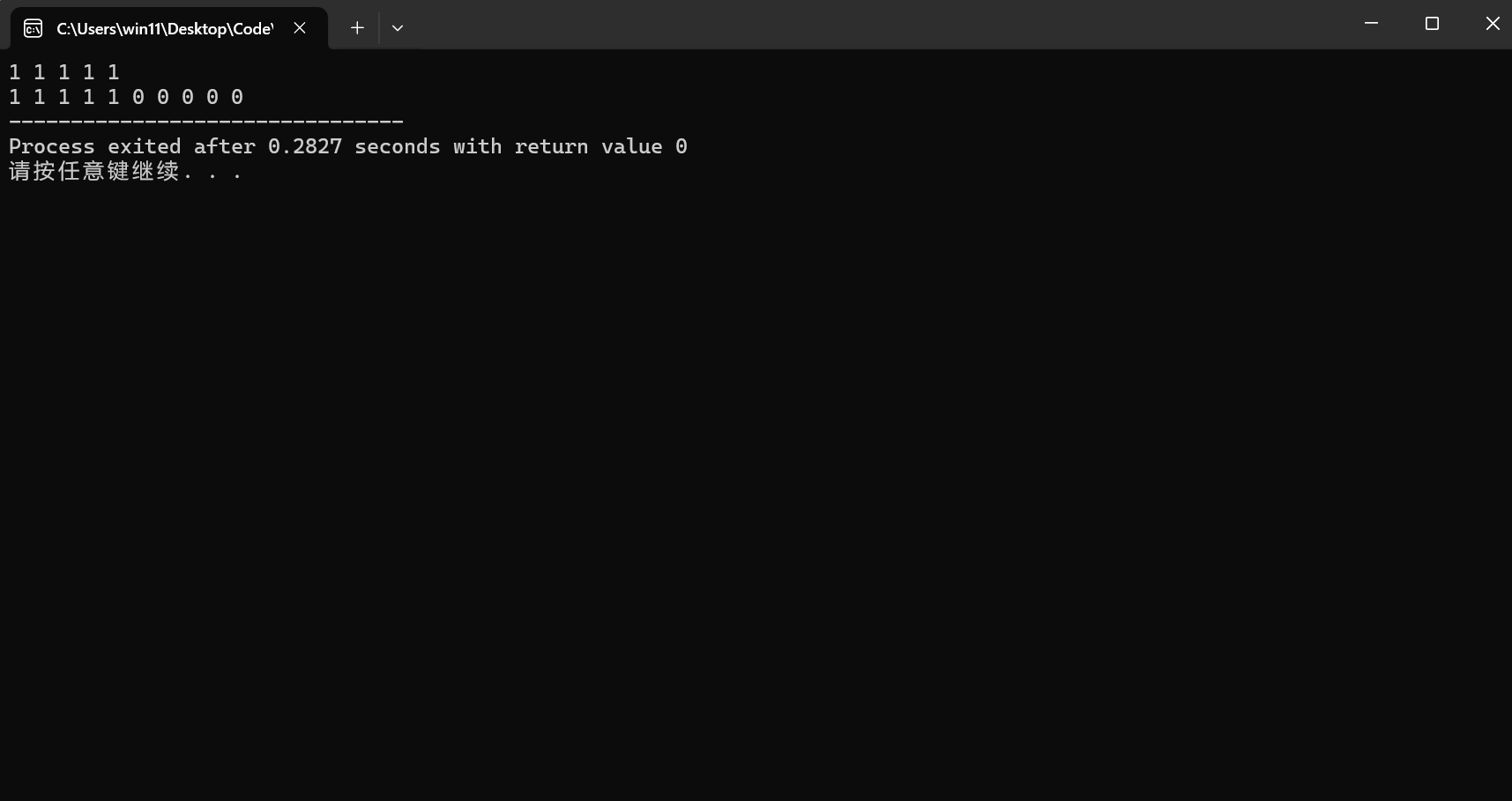
6.resize
- 修改vector的大小
- 如果大于原始的大小,多出来的位置上会补上默认值0
- 如果小于原始大小,相当于把后面的元素给删掉
- 时间复杂度:O(N)
代码演示:
cpp
#include<iostream>
#include<vector>
using namespace std;
int main()
{
vector<int> a(5,1);
for(auto i:a) cout<<i<<" ";
cout<<endl;
a.resize(10);
for(auto i:a) cout<<i<<" ";
return 0;
}
7.clear
清空vector,底层实现时,会遍历整个数组,一个一个删除,因此时间复杂度为:O(N)
二.vector相关算法题
1.洛谷---询问学号
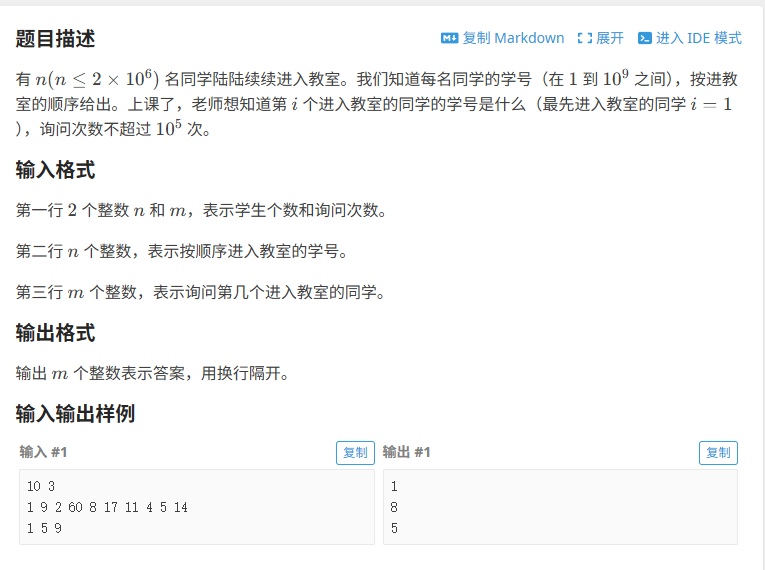
代码:
cpp
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n,m;cin>>n>>m;
vector<int> a(n+1,0);
for(int i=1;i<=n;i++) cin>>a[i];
while(m--)
{
int f;cin>>f;
cout<<a[f]<<endl;
}
return 0;
}2.洛谷---寄包柜
代码:
cpp
#include<iostream>
#include<vector>
using namespace std;
int main()
{
int n,q;
cin>>n>>q;
vector<int> a[n+1];//行确定列不确定,即柜子数确定但每个柜子的格子数不确定
while(q--)
{
int flag,i,j,k;
cin>>flag>>i>>j;
if(flag == 1)//存
{
cin>>k;
if(a[i].size()<=j)
a[i].resize(j+1);
a[i][j]=k;
}
else//查询
cout<<a[i][j]<<endl;
}
return 0;
}3.leetcode---颜色分类

不用sort函数完成对nums数组的排序,数组中只有 0、1、2 三种类型的数字
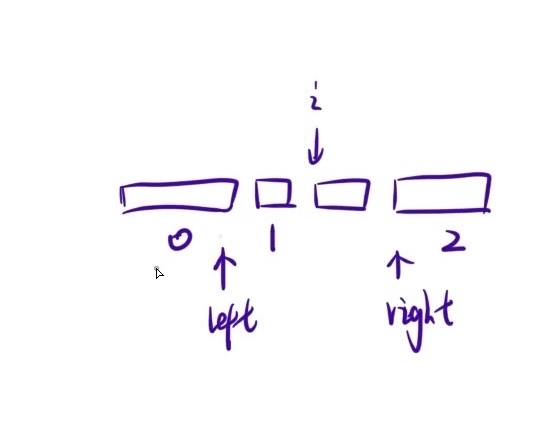
解法:三指针
如上图所示,定义三个指针:
- i :扫描数组
- left :标记的就是 0 区间的最后一个元素
- right :标记的是 2 区间的第一个元素
[0,left]:0区间 [left+1,i-1]:1区间
[i,right-1] :待扫描 [right,n-1]:2区间
当 i 与 right 相遇时,说明没有待扫描的了,可以结束循环
细节问题:
初始化时,left = -1,right = n ,因为此时 0 区间 与 2区间 都没有元素,所以都指向数组外的位置;当 i 下标的元素为 2 时,让 right-- 后与 i 位置元素交换,此时千万不要让 i 往后,因为从right-1位置交换过来的元素还没有进行判断 ;当i 下标的元素为 1 时,直接 i++ 即可 ,因为 i 的扫描是针对 0、2区间的当中区间(通过元素交换实现),而这个当中区间正好是 1区间;当i 下标的元素为 0 时,让 left++ 后与 i 位置交换 ,left + 1 位置指向 1区间,并且 0->i-1区间是已经扫描完毕的,所以left+1 位置交换过来的元素只可能是 1,因此交换后 i++
代码:
cpp
class Solution {
public:
void sortColors(vector<int>& nums) {
int n=nums.size();
for(int i=0,left=-1,right=n;i<right;)
{
if(!nums[i]) swap(nums[i++],nums[++left]);
else if(nums[i]==2) swap(nums[i],nums[--right]);
else i++;
}
}
};4.leetcode---合并两个有序数组

非递减顺序:不是严格递增的递增数列,即升序排序的同时可能会有2个数相等
代码1(辅助数组):
cpp
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int cur1 = 0,cur2 = 0;
vector<int> tmp(m+n,0);
int i=0;
while(cur1<=m-1&&cur2<=n-1)
{
if(nums1[cur1]<=nums2[cur2]) tmp[i++] = nums1[cur1++];
else tmp[i++] = nums2[cur2++];
}
while(cur1<=m-1)tmp[i++] = nums1[cur1++];
while(cur2<=n-1)tmp[i++] = nums2[cur2++];
i = 0;
for(int x:tmp) nums1[i++]=x;
}
};代码2(逆序原地遍历):
cpp
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int cur = m+n-1,cur1 = m-1,cur2 = n-1;
while(cur1>=0&&cur2>=0)
{
if(nums1[cur1]<=nums2[cur2])nums1[cur--]=nums2[cur2--];
else nums1[cur--]=nums1[cur1--];
}
while(cur1>=0)nums1[cur--]=nums1[cur1--];
while(cur2>=0)nums1[cur--]=nums2[cur2--];
}
};代码解释:
如下图1所示,如果正序遍历会导致nums1原来有的值被覆盖,所以我们可以采取正难则反的思想,都从区间的末尾向前遍历(如下图2所示)
当cur1位置元素大时,换cur1;当cur2位置元素大时,换cur2;无论是哪个去换,换完了需要向前走一个位置

图1
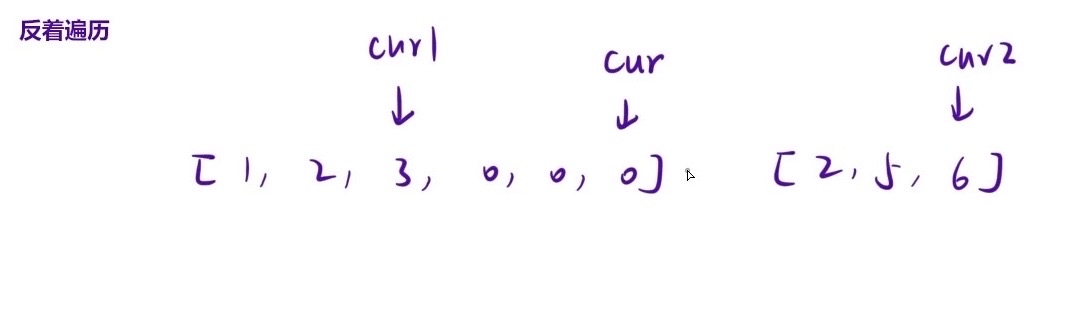
图2
5.洛谷(UVA)---The Blocks Problem

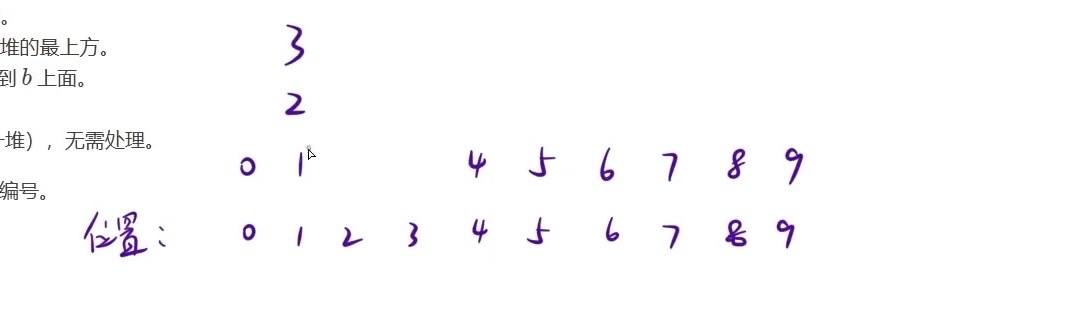
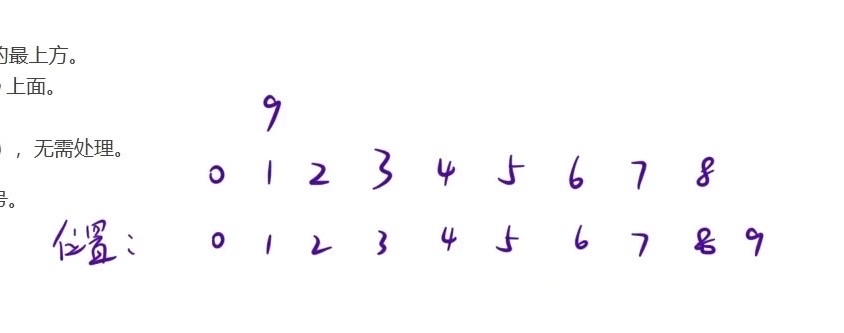
归位即是把2、3两个数字移动到2、3位置,数字对应位置移动
然后再把 9 放到 1 上
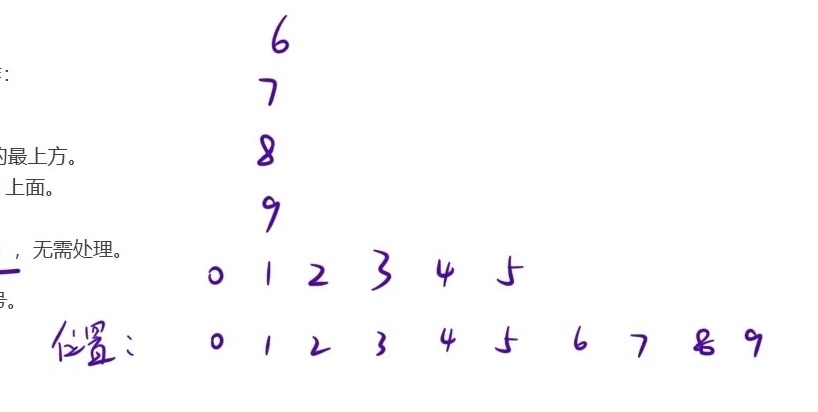
归位+移动,把8、7、6移动到了1上,pile 8 over 6 因为 8 与 6 在同一堆上,所以跳过执行
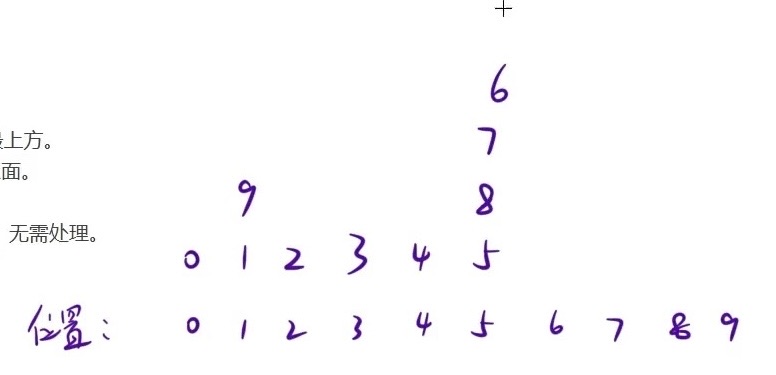
pile 8 over 5 即把 8 及其上面所有的元素都移动到 5 上面
pair介绍:
pair是C++中的一个模板类,用于将两个值组合成一个单一对象,可以看成一个结构体
struct pair
{
type first;
type second;
}
其中type类型是任意的( int、string......),初始化时是 pair<type,type> p_name
调用第一个值:p.first 调用第二个值:p.second
解法:模拟
1.找到 4 种操作分别具有的共同点(比如无论 move 后面跟的是onto还是over,都需要把a上方的元素归位)
- move:a 上方归位
- pile:a 及 a 上方放到 b 上
- onto:b 上方归位;a 及 a 上方放在 b 上(move a onto b 虽然是把 a 放到 b 上,但由于已经把 a 上方的元素全部归位了,所以 a 及 a 上方就相当于 a)
- over: a 及 a 上方放在 b 上(与把 a 放到 b 上一样,理由同上)
因此我们可以把操作分为两类:归位、移动
换言之,我们只需要两个函数就能够解决所有问题
如何用代码实现这个过程?
二维数组,行作为位置列作为该位置存放的木块;当我们要移动时就是遍历所有 指定元素与指定元素的上方元素(如下图所示),然后转移到 指定元素的上方 去(通过尾插的方法)
每次寻找完指定元素,我们都得用它的 指定位置 来进行遍历,而 指定位置 会有行与列2个值,因此我们可以使用 pair 来实现
何时结束操作?
可以通过 while(cin>>str1>>a>>str2>>b) 这条语句来实现,当 输入内容 少于4个的时候,即只输入了 quit,那么会为 false 结束循环,自测的时候用 ctrl + z + 回车 结束
代码:
cpp
#include<iostream>
#include<vector>
using namespace std;
const int N = 30;
int n;
vector<int> wood[N];//总共有N个槽位
typedef pair<int, int> PII;
PII find(int x)
{
for (int i = 0;i < n;i++)
for (int j = 0;j < wood[i].size();j++)
if (x == wood[i][j]) return{ i,j };
}
void clean(int x, int y)//两个值分别为要移动的值所在槽位,以及要移动值的开始位置
{
for (int j = y + 1;j < wood[x].size();j++)
{
int tmp = wood[x][j];
wood[tmp].push_back(tmp);
}
wood[x].resize(y + 1);
//重新设置大小,[0,y]下标的值留下了,[y,size-1]的值被移走了,新的大小应该为 y+1
}
void move(int x1, int y1, int x2)//最后一个值为要移动到的位置
{
for (int j = y1;j < wood[x1].size();j++)
wood[x2].push_back(wood[x1][j]);
wood[x1].resize(y1);
}
int main()
{
cin >> n;
string op1, op2;
int a, b;
//初始化
for (int i = 0;i < n;i++)
wood[i].push_back(i);
//开始操作
while (cin >> op1 >> a >> op2 >> b)
{
//找位置
PII pa = find(a);
PII pb = find(b);
int x1 = pa.first, y1 = pa.second;
int x2 = pb.first, y2 = pb.second;
//开始根据输入进行操作
if (x1 == x2) continue;//在同一个槽位
if (op1 == "move") clean(x1, y1);//a的上方归位
if (op2 == "onto") clean(x2, y2);//b的上方归位
move(x1, y1, x2);//移动
}
for (int i = 0;i < n;i++)
{
cout << i << ":";
for (int j = 0;j < wood[i].size();j++)
cout << " " << wood[i][j];
cout << endl;
}
return 0;
} 代码易错点:
for循环的退出条件得是 < wood[x].size() ,不能是 <= wood[x].size() - 1 ,可能会有数组溢出的风险