本文仅用作自己学习,补充张宇30讲没有涉及的内容
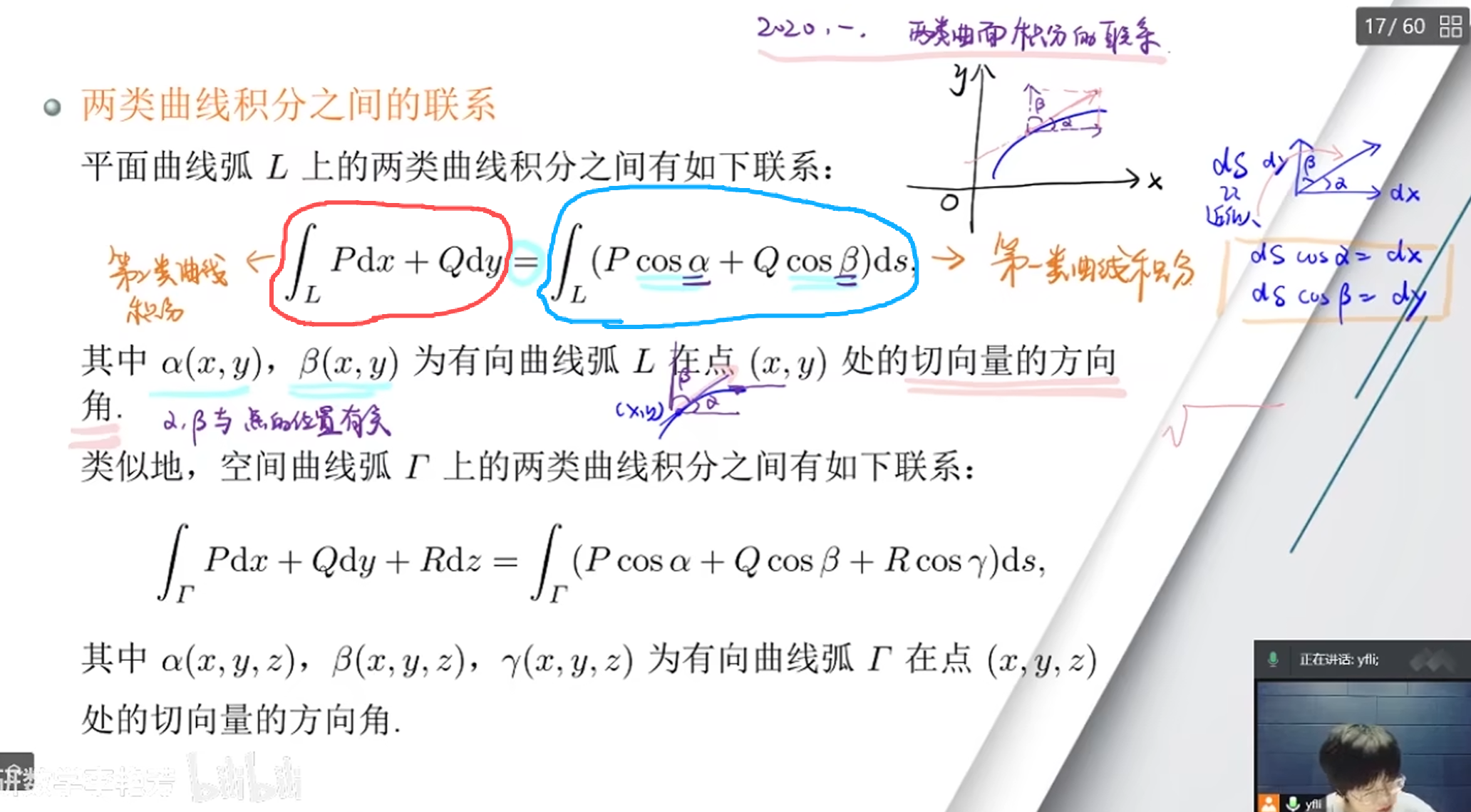
第一类曲线积分和第二类曲线积分的关系
其中第二类曲线积分其实可以变成第一类曲线积分红色的是第二类,蓝色的是一类
其中我们其实可以发现右图中,我们可以取一个微元弧长,把它近似的看成是直线
而cosα和coaβ是该微元上的切向量,因为是微元,所以和直线的方向近似相等
那么ds为该微元弧长,当其×向量角的时候就可以该微元在x轴和y轴的分量
即dx和dy微元
然后就可以将其化为第二类曲线积分,同理第二类也可以转化为第一类
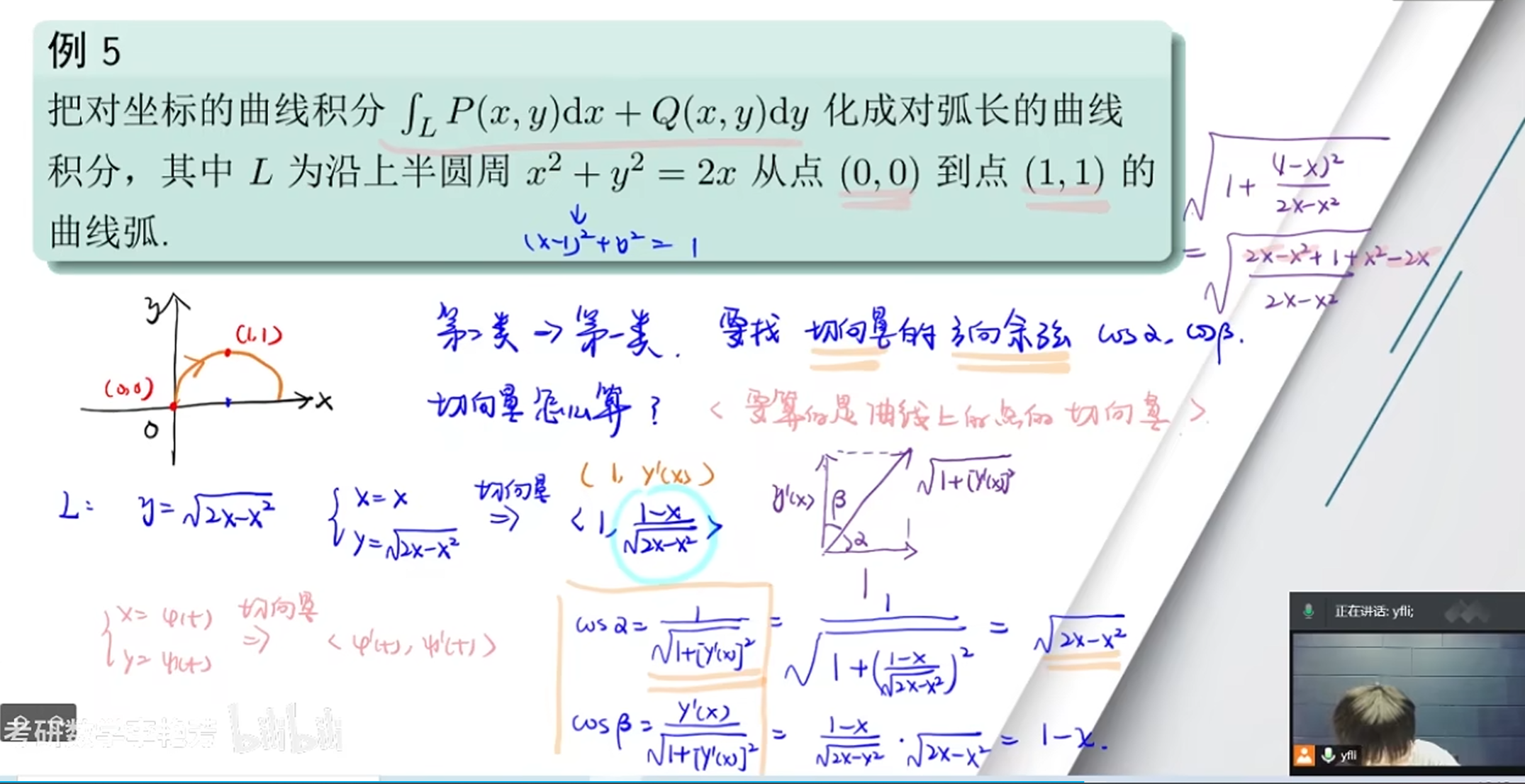
例题
对于求cosα和cosβ我们可以求某点的切向量然后计算方向角,而切向量计算过程如下,空间解析几何的内容
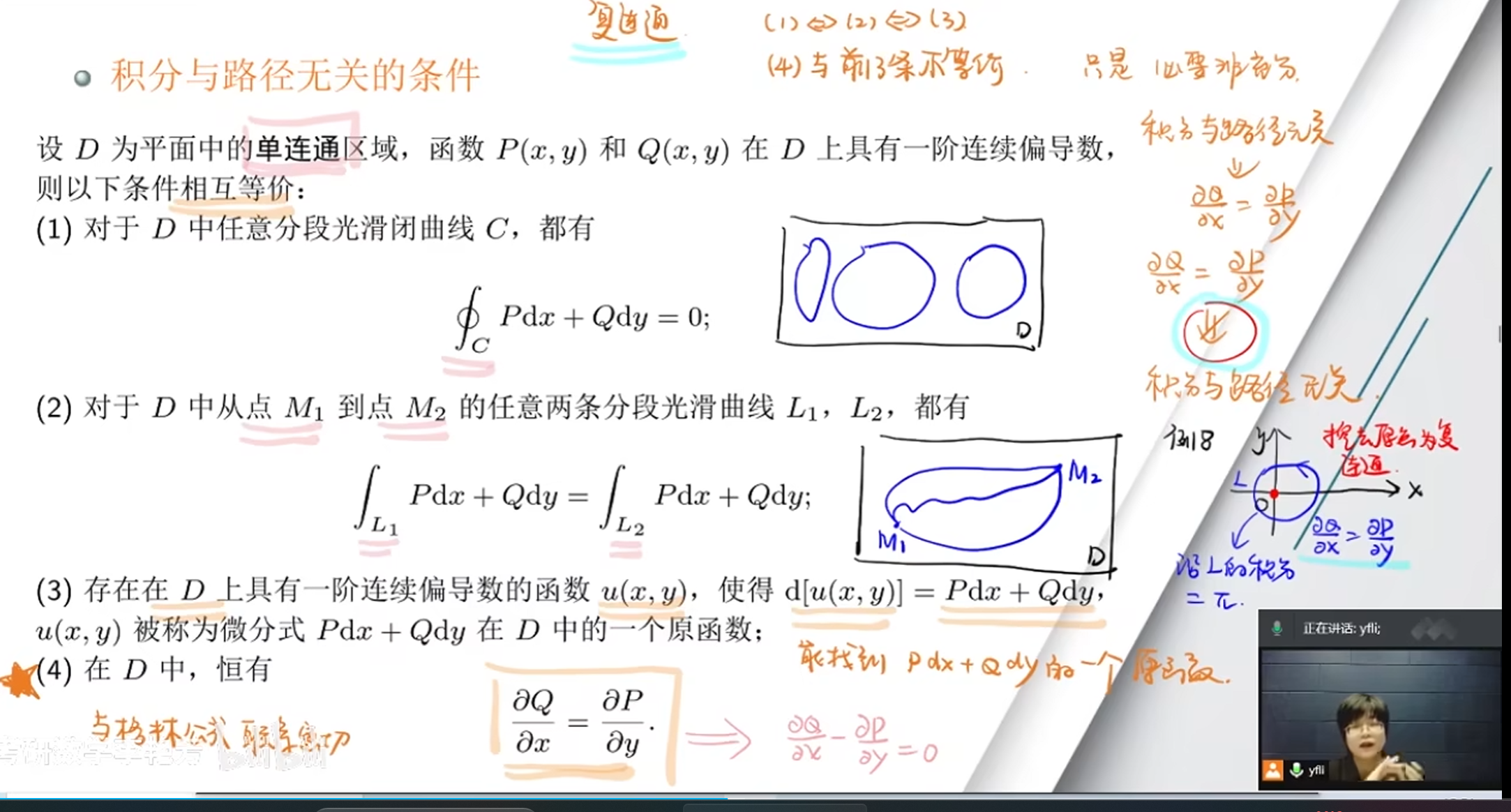
积分与路径无关的条件
如下条件即可判断积分与路径无关
条件三的判断方法是如果能够找到一个P和Q积分的原函数的话,即全微分那么也可以判断积分与路径无关
其中4和格林公式密切相关,即两个相减满足格林公式
其中什么叫做单连通,即没有奇点的区域
三和一二等价,有一你就有三,有三你就有一,如果一个被积函数有原函数则其必为0当其积分曲线为封闭时

曲线积分的基本定理
本质还是找全微分
当存在一个函数的全微分等于第二类曲线积分的被积函数的时候
我们可以得到对第二类曲线积分有
其原函数的起点值减去终点值
由牛顿莱布尼茨公式推广




若Q和P的偏导相等,则说明其有原函数,则我们可以求全微分
然后我们就可以通过折线法算积分值计算得到u(x,y)相差一个常数不影响u(x,y)

第二类曲面积分的定义
和🐙的书不同,他说的是关于xy的曲面积分
本人对此有疑问,先写在这

如何判断侧?
以上半球面的上侧下侧为例,如过曲面的侧是上侧,取某点的法向量来看,那么其指向的应该是z轴的正方向,即沿着z轴的分量为整数,即z为正数,根据法向量的定义(F'x,F'y,F'Z)即可求得
其他的也是如此判断

现在回过头看定义,投影到某个面时,若他们的方向向量有与轴的夹角≠0,其投影就是曲面面积乘以方向向量的那个角,面积无正负但是夹角有正负

第二类曲面积分计算

两类曲面积分的联系和相互转化
相互转化右图所示
注意是法向量的方向余弦

注意可以讲dydz和dzdy全部转化为dxdy
注意它们之间的联系,投影到哪则消去哪,并乘以对应的夹角
比如投影到dydz面,则ds×cosα(即与x轴的方向角)

第二类曲面积分的对称性
即奇函数是二倍,偶函数是0



合一投影法
转换为一个曲面上进行积分


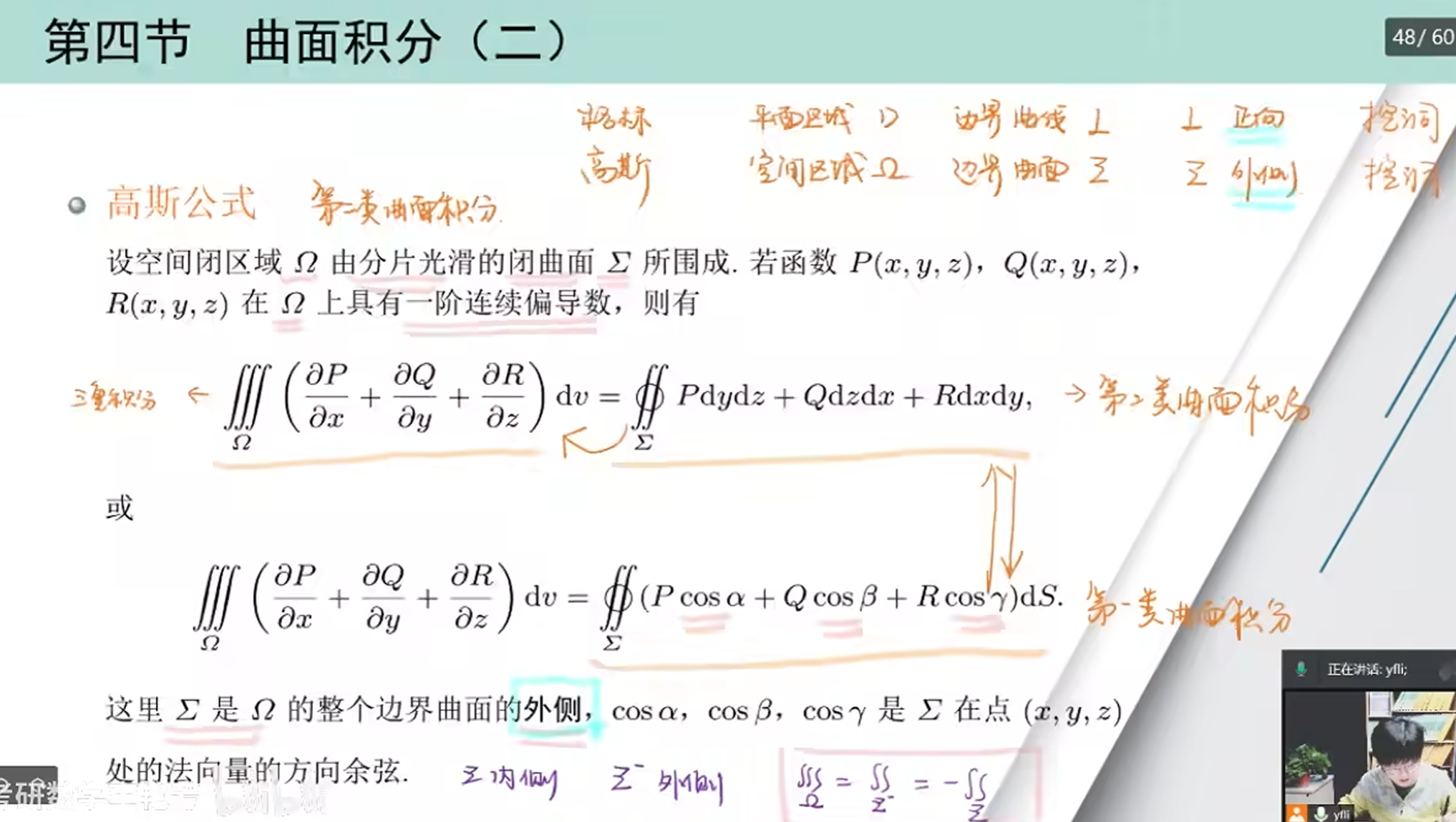
高斯公式
注意类比其和格林公式的异同点
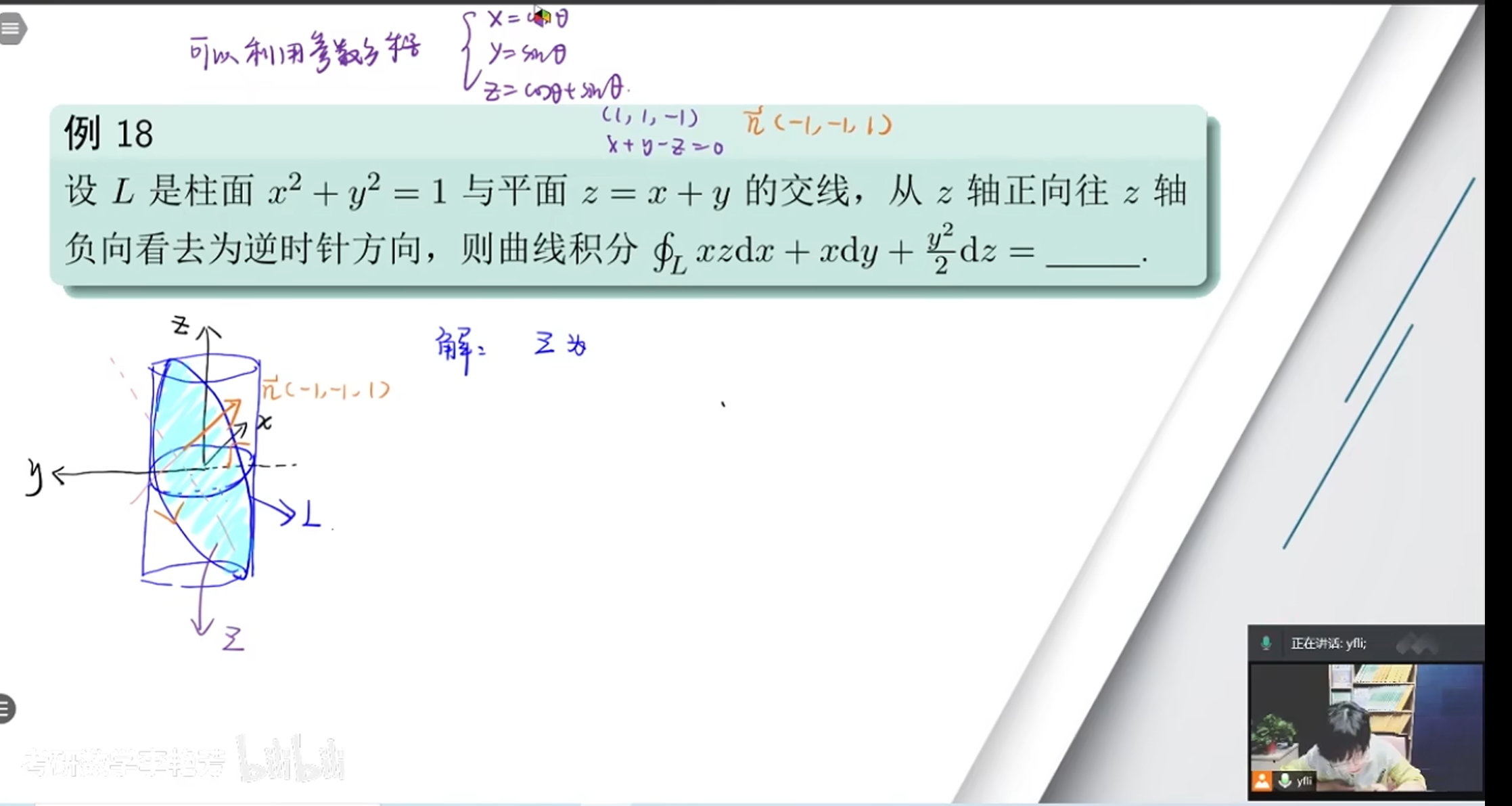
例题

散度
本质还是高斯公式
记住散度的概念即可


斯托克斯公式



旋度
本质斯托克斯公式,可以代行列式计算


做题要点
积分区域关于y=x对称则具有轮换对称性

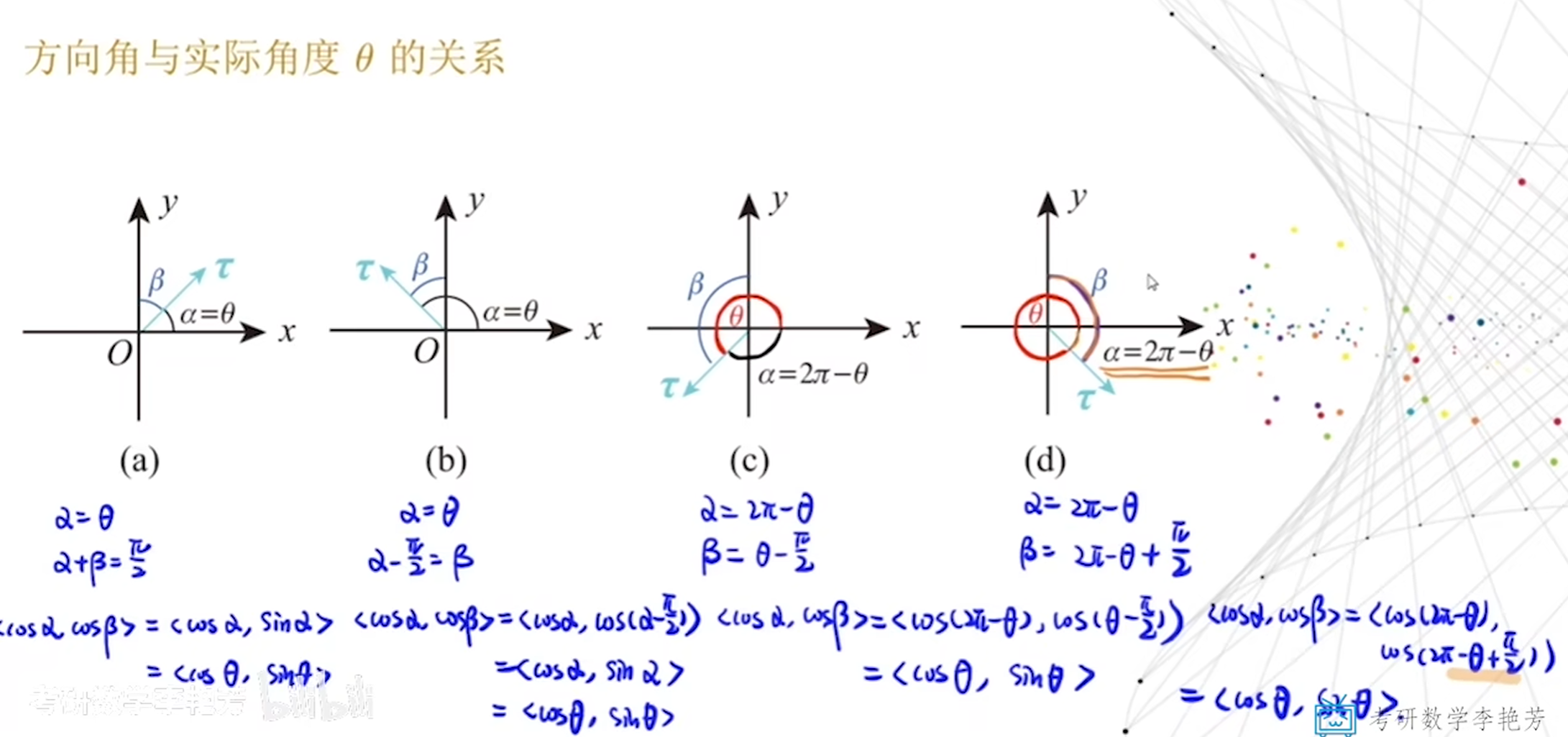
方向角和实际角度θ的关系