文章目录
感知机和SVM
感知机
对上述文章部分内容进行额外补充和解释:

这里的"在训练数据集中选取数据(x,y)"具体是如何选取的?

通俗解释:

SVM(支持向量法)
二者联系和区别
感知机(Perceptron)和支持向量机(Support Vector Machine, SVM)都是经典的线性分类器 ,它们旨在找到一个能够将不同类别数据分开的超平面。SVD可以认为是基于感知机基础上的改进。
区别:
主要是下图标注的地方内容

GRU和LSTM

GRU
额外补充:

上述内容的记忆和遗忘是针对新的候选信息 h ^ t \hat h_t h^t!GRU通过一个更新门 z t z_t zt同时控制遗忘和更新,当 z t z_t zt很大,就意味着大量遗忘旧信息并大量吸收新信息;如果 z t z_t zt很小,就意味着大量保留旧信息并大量忽略新消息。它没有 LSTM 那样独立地"只遗忘一部分旧信息,但完全不吸收新信息"的能力。

LSTM
二者区别与联系
联系:
上述两者都是基于循环神经网络(RNN)的改进,可以解决RNN中不能长期记忆和反向传播中的梯度等问题。它们通过引入门控机制来选择性地记忆和遗忘信息。
区别:
主要的区别在于它们的内部结构、门的数量以及门控机制的实现方式。
1.门控机制和数量
LSTM有是三个门,俩状态 :

两个状态分别为:
(1).细胞状态 C t C_t Ct

(2).隐藏状态 h t h_t ht

细胞状态 ( C t C_t Ct) 负责长期信息的存储和传输,是 LSTM 核心的记忆通道。
隐藏状态 ( h t h_t ht) 负责当前时间步的输出,并在一定程度上也携带了信息,参与到下一个时间步的门控计算中。
GRU有两个门:

2.内部结构与状态

3.对信息的控制粒度

4.参数数量和计算效率

正则化
正则化存在的意义,能帮助我们在训练模型的过程中,防止模型过拟合。在不减少模型特征参数的前提情况下,降低模型的复杂程度。
为什么正则化约束可以防止模型过拟合?

通过约束参数的数值,从而限制模型的复杂程度。
L1正则化和L2正则化

图中的"L2正则化只能使得模型的参数数值趋于零,但不能等于0,而L1正则化却可以"内容,这是为什么?
下图从数学角度分析:

文章中也有从几何方式解释内容:
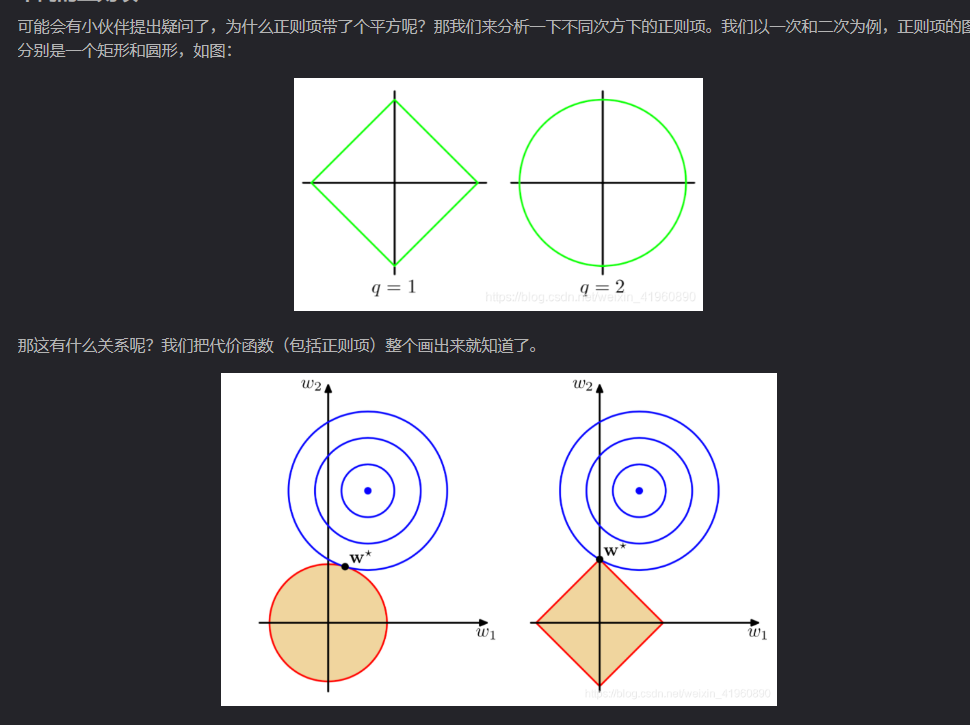
上述图是从二维空间进行分析,(坐标系分别对应 w 1 , w 2 w_1,w_2 w1,w2)
注:带正则化的约束问题的目标函数是: m i n w L ( w ) + t R ( w ) min_wL(w)+tR(w) minwL(w)+tR(w),可以转化为带有约束的形式为 m i n w L ( w ) , s . t . R ( w ) < = T min_wL(w) ,s.t.R(w)<=T minwL(w),s.t.R(w)<=T。
图具体表示什么意思:图中的蓝色图像表示的是损失函数的等高线(代表 L ( w ) L(w) L(w)的值) , 图中的红色图像分别表示的是L2正则化约束区域和L1正则化约束区域(代表了 R ( w ) < = T R(w)<=T R(w)<=T的区域,优化算法只能在这个区域内寻找解,否则 w w w值过大,则会使得带约束的问题目标函数数值很大)。
L2正则化目标函数公式:
m i n w ( L ( w ) + t ∣ ∣ w ∣ ∣ 2 2 min_w(L(w)+t||w||_2^2 minw(L(w)+t∣∣w∣∣22
其中的蓝色的圆的半径长度对应的就是 L ( w ) L(w) L(w)数值,红色的图形中,红色圆表示的是L2正则化约束范围,即 t ∣ ∣ w ∣ ∣ 2 2 t||w||_2^2 t∣∣w∣∣22(原点到红色边的距离),
同理:
L1正则化目标函数公式:
m i n w ( L ( w ) + t ∣ ∣ w ∣ ∣ 1 ) min_w(L(w)+t||w||_1) minw(L(w)+t∣∣w∣∣1)
红色菱形图形表示的就是L1正则化约束范围,即 t ∣ ∣ w ∣ ∣ 1 t||w||_1 t∣∣w∣∣1(原点到红色边的距离)。
我们想要求目标函数数值最低时的 w w w数值,即红色图像和蓝色图像关于某个点( w w w)的距离之和最小。这个数值往往是蓝色和红色这两个图像的相切地方。