《算法与数据结构》第六章[第4节]：哈夫曼树

一、哈夫曼树及其应用

话说前面我们学了各种各样的树，有普通的树、二叉树、线索二叉树，这些树主要解决的是数据的组织和遍历问题。那有同学就要问了，树还能干什么呢？别急，今天我们就来看看树在数据压缩方面的神奇应用。

假设你现在是一名网络工程师，你的老板交给你一个任务：公司要传输一份重要文档，这份文档包含100万个字符，主要由字母A、B、C、D、E组成，它们的出现频率如下：

字符	A	B	C	D	E
出现频率(万次)	45	13	12	16	14

老板说网络带宽很宝贵，要求你尽可能减少传输的数据量。你想，最简单的编码方案就是给每个字符分配固定长度的二进制码：

字符	A	B	C	D	E
编码	000	001	010	011	100

这样传输100万个字符需要：100万 × 3 = 300万位

但你突然灵光一现，既然A出现得最频繁(45万次)，为什么不给它分配更短的编码呢？而那些出现较少的字符可以用长一点的编码。比如：

字符	A	B	C	D	E
编码	0	101	100	11	110

这样传输同样的100万个字符需要：45万×1 + 13万×3 + 12万×3 + 16万×2 + 14万×3 = 45 + 39 + 36 + 32 + 42 = 194万位

这样下来就节省了106万位，压缩率达到了35%！老板肯定会给你加薪的。

但紧接着你就犯愁了：这种变长编码会不会产生歧义呢？比如序列"101"，它到底是表示B(101)，还是D的结尾(1)+A(0)+D的开头(1)？如果解码时产生歧义，那传输的数据就完全错乱了。

经过仔细思考，聪明的你发现了一个规律：只要保证任何字符的编码都不是另一个字符编码的前缀 ，就不会产生歧义。在上面的例子中，A的编码是"0"，而其他字符的编码都不是以"0"开头的，所以不会有问题。

现在问题来了：对于给定的字符及其出现频率，如何构造出传输总长度最短且无歧义的编码方案？

当然，若是聪明的你没有看懂上述内容，也没关系，以上就是我们今天要学习的哈夫曼树(Huffman Tree)要解决的核心问题。它不仅能帮我们找到最优的编码方案，在文件压缩、图像压缩、甚至音频压缩等领域都有广泛应用。ZIP文件、JPEG图片、MP3音乐，它们的压缩算法中都有哈夫曼编码的身影。

1、哈夫曼树

相信大家在编程语言的分支语句学习时都写过或见过下面这个程序：

#include <stdio.h>

int main()
{
	float score;
	printf("请输入成绩：");
	scanf("%f", &score);
	if (score >= 90)
		printf("优秀\n");
	else if (score >= 80)
		printf("良好\n");
	else if (score >= 70)
		printf("中等\n");
	else if (score >= 60)
		printf("及格\n");
	else
		printf("不及格\n");
	return 0;
}

由于计算机程序运行效率之高，我们可能不会在意这个程序的效率问题，但如果我们要处理的是海量数据呢？比如需要对全校的成绩进行分类，在这样的尺度下效率就愈显重要了。我们先把这个程序的执行过程画成一棵流程树：

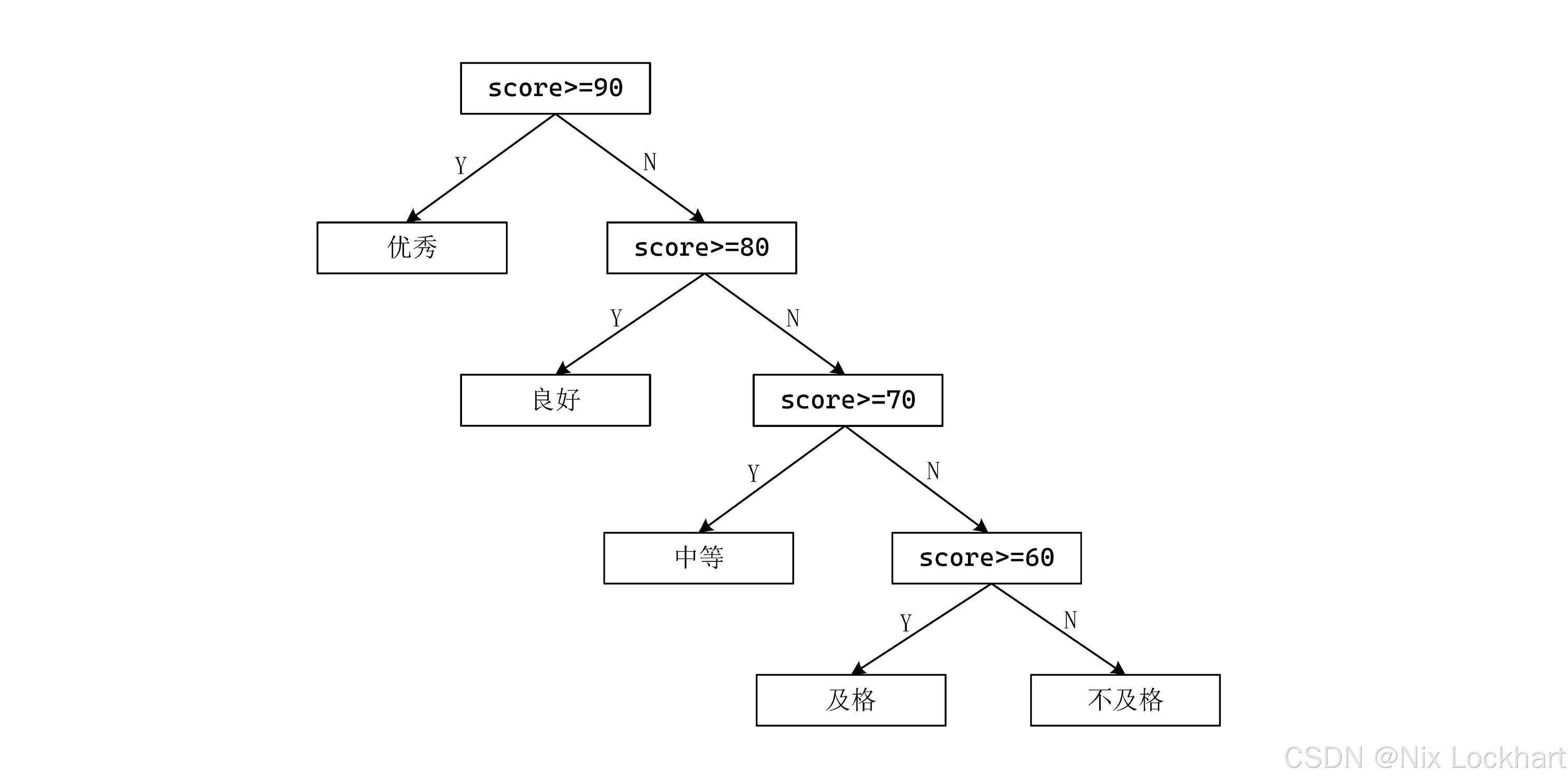
图1：成绩分类流程树

可以看到，程序的执行过程就是从根结点出发，沿着树的分支一路走到叶子结点。每次判断都要花费一定时间，假设每次判断花费1个单位时间，那么：

• 如果成绩在90分及以上，只需要1个单位时间就能得到结果；
• 如果成绩在80~89分之间，需要2个单位时间；
• 如果成绩在70~79分之间，需要3个单位时间；
• 如果成绩在0~69分之间，需要4个单位时间；

但是大家都知道，成绩分布一般都是正态分布的，大部分成绩都集中在中间段，即70-89分之间，而90分及以上和60分以下的成绩相对较少。例如下表所示的情况：

成绩段	90-100	80-89	70-79	60-69	0-59
人数(%)	5%	40%	30%	15%	10%

这样一来，多数判断都需要2-3个单位时间，那我们能不能把70-89分的成绩判断得更快一些呢？也就是说，我们能不能让70-89分的成绩离根结点更近一些？

我们把上面的流程树稍微调整一下：

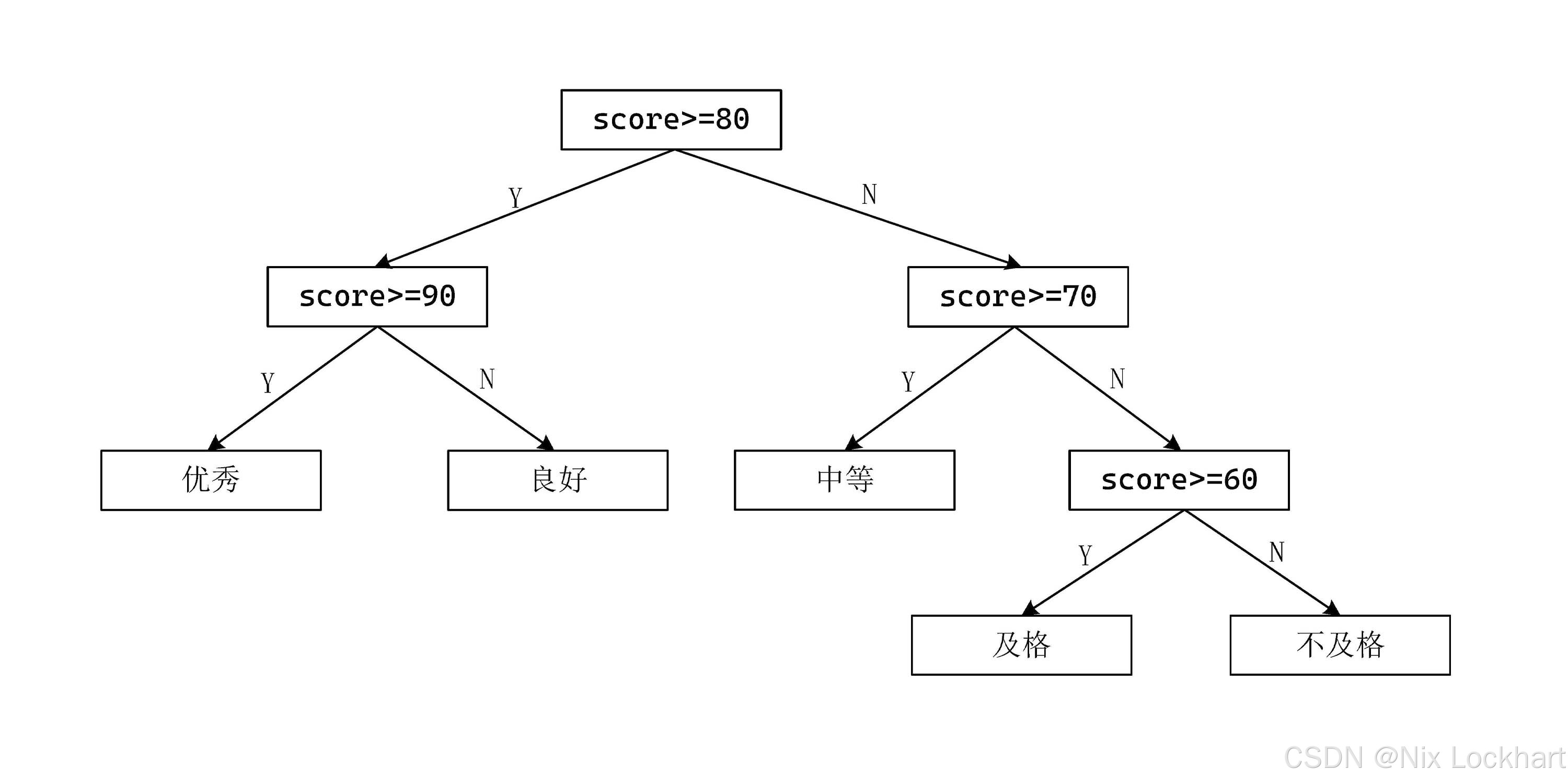
图2：调整后的成绩分类流程树

可以看到，70-89分的成绩离根结点更近了，平均判断时间也缩短了。

这就是哈夫曼树的核心思想：根据各个结点的权值(频率)来调整树的结构，使得权值较大的结点离根结点更近，从而减少平均路径长度(平均判断时间)。

2、哈夫曼树的定义与原理

我们先把上文中的流程树转化为一棵带权二叉树(权重即为频率)，如下图所示：

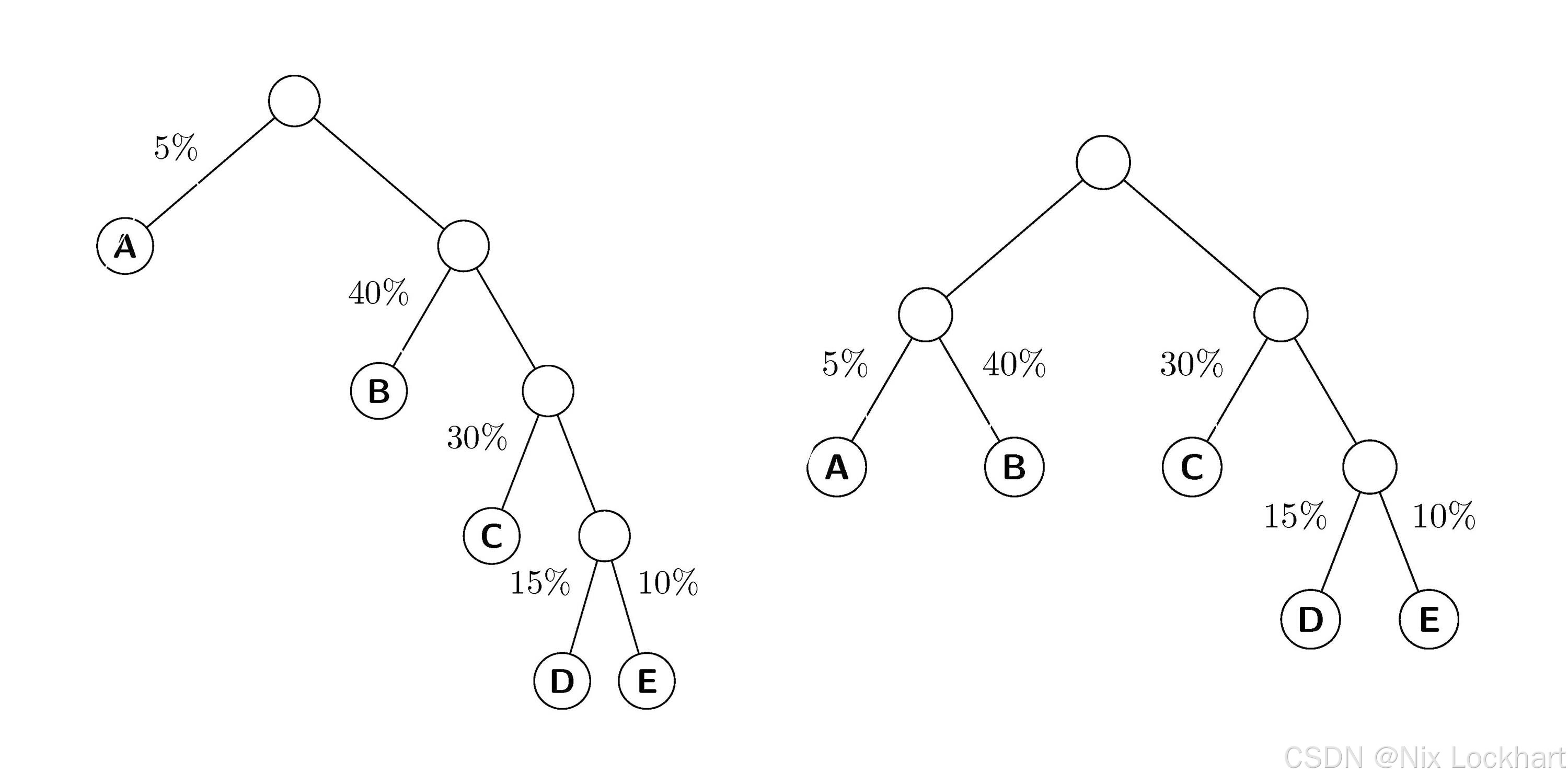
图3：成绩分类带权二叉树

首先我们来了解路径和路径长度的概念：

• 路径：树中一个结点到另一个结点之间的分支构成这两个结点的路径。
• 路径长度：路径上的分支数目称做路径长度。
• 树的路径长度 ：从树根到++每一个结点++的路径长度之和称为树的路径长度。

如图3左图所示，根结点到结点DDD的路径长度就为4(经过4条分支)，而右图中，根结点到结点DDD的路径长度为3(经过3条分支)。我们可以看到，右图的树的路径长度小于左图的树的路径长度。

左图二叉树的路径长度为：
1+1+2+2+3+3+4+4=201+1+2+2+3+3+4+4=201+1+2+2+3+3+4+4=20

右图中的二叉树的路径长度为：
1+2+2+1+2+2+3+3=161+2+2+1+2+2+3+3=161+2+2+1+2+2+3+3=16

可以看到，右图的二叉树路径长度更小。

若考虑到各个结点的权值(频率)，我们可以给出定义

• 带权路径长度：从该结点到树根之间的路径长度与该结点的权值的乘积称为该结点的带权路径长度。
• 树的带权路径长度：树中所有叶子结点的带权路径长度之和称为树的带权路径长度，记作WPL(Weighted Path Length)。

假设有nnn个权值{w1,w2,...,wn}\{w_1,w_2,...,w_n\}{w1,w2,...,wn}，构造一棵带有nnn个叶子结点的二叉树TTT，其中第iii个叶子结点的权值为wiw_iwi，每个叶子结点的路径长度为lil_ili，则有

WPL=∑i=1nwiliWPL=\displaystyle\sum_{i=1}^{n}{w_il_i} WPL=i=1∑nwili

其中带权路径长度最小的二叉树称做哈夫曼树(Huffman Tree)，也叫赫夫曼树(音译区别)，或者还有些书中称它为最优二叉树。

有了以上定义，我们可以计算出图3中两棵树的带权路径长度：

• 左图：5×1+40×2+30×3+15×4+10×4=2755\times1 + 40\times2 + 30\times3 + 15\times4 + 10\times4 = 2755×1+40×2+30×3+15×4+10×4=275
• 右图：5×2+40×2+30×2+15×3+10×3=2255\times2 + 40\times2 + 30\times2 + 15\times3 + 10\times3 = 2255×2+40×2+30×2+15×3+10×3=225

算式1中前两项中的555是结点AAA的权值，111是结点AAA的路径长度；后续404040是结点BBB的权值，222是结点BBB的路径长度。其他项同理。

在当前这个数量级(100)下，只有50的差距，但如果数据量更大，差距就会更明显了。

那么我们该如何获得一棵哈夫曼树呢？哈夫曼早已给出了树的构造算法如下：

1. 根据给定的nnn个权值{w1,w2,⋯ ,wn}\{ w_1, w_2, \cdots , w_n\}{w1,w2,⋯,wn}构成nnn棵二叉树的集合F={T1,T2,⋯Tn}F=\{ T_1, T_2, \cdots T_n \}F={T1,T2,⋯Tn}，其中每棵二叉树TiT_iTi仅有一个结点，其权值为wiw_iwi，其左右子树均为空；
2. 在集合FFF中选取两棵权值最小的二叉树TiT_iTi和TjT_jTj，构造一棵新的二叉树TijT_{ij}Tij，其根结点的权值为wi+wjw_i+w_jwi+wj，左子树为TiT_iTi，右子树为TjT_jTj；
3. 从集合FFF中删除二叉树TiT_iTi和TjT_jTj，并将新构造的二叉树TijT_{ij}Tij加入集合FFF；
4. 重复步骤2和3，直到集合FFF中只剩下一棵二叉树为止，这棵二叉树即为所求的哈夫曼树。

我们来通过一个例子理解一下哈夫曼树的构造过程，假设我们有5个结点情况如下表，我们来一步步构造哈夫曼树。

结点	A	B	C	D	E
权值	5	40	30	15	10

首先我们将每个结点都看作一棵单结点的二叉树，构成集合：

F={TA(5),TB(40),TC(30),TD(15),TE(10)}F=\{T_A(5), T_B(40), T_C(30), T_D(15), T_E(10)\}F={TA(5),TB(40),TC(30),TD(15),TE(10)}

为方便起见，我们提前将集合中的二叉树按权值从小到大排序，便于我们每次选取权值最小的两棵二叉树。则有：

F={TA(5),TE(10),TD(15),TC(30),TB(40)}F=\{T_A(5), T_E(10), T_D(15), T_C(30), T_B(40)\}F={TA(5),TE(10),TD(15),TC(30),TB(40)}

然后，我们选取权值最小的两棵二叉树TAT_ATA和TET_ETE，构造一棵新的二叉树T1T_{1}T1，其根结点的权值为5+10=155+10=155+10=15，左子树为TAT_ATA，右子树为TET_ETE，如下图所示：

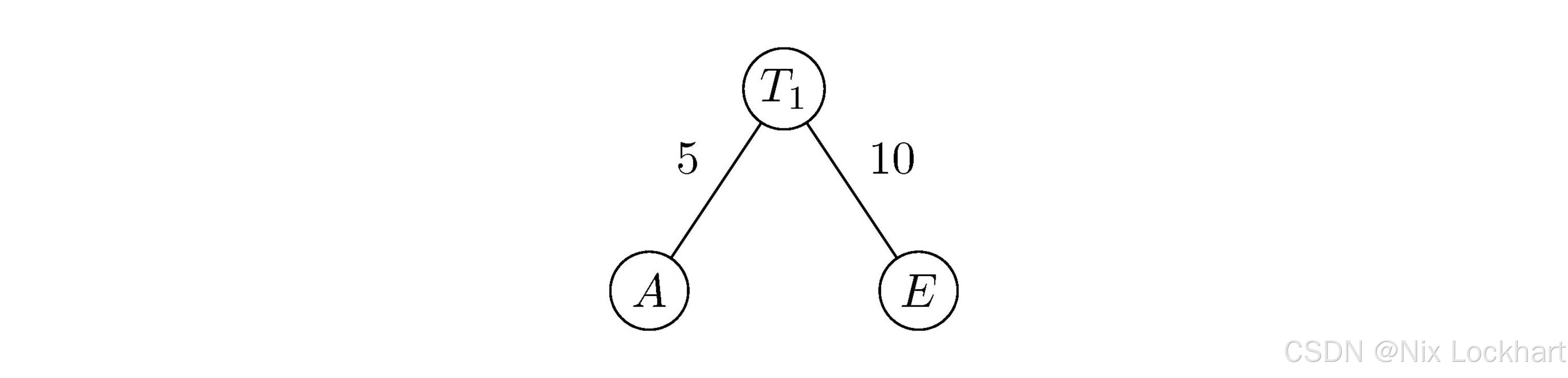
图4：构造二叉树1

然后我们从集合FFF中删除二叉树TAT_ATA和TET_ETE，并将新构造的二叉树T1T_{1}T1加入集合FFF，则有：

F={T1(15),TD(15),TC(30),TB(40)}F=\{T_{1}(15), T_D(15), T_C(30), T_B(40)\}F={T1(15),TD(15),TC(30),TB(40)}

接下来，我们继续选取权值最小的两棵二叉树T1T_{1}T1和TDT_DTD，构造一棵新的二叉树T2T_{2}T2，其根结点的权值为15+15=3015+15=3015+15=30，左子树为T1T_{1}T1，右子树为TDT_DTD，如下图所示：

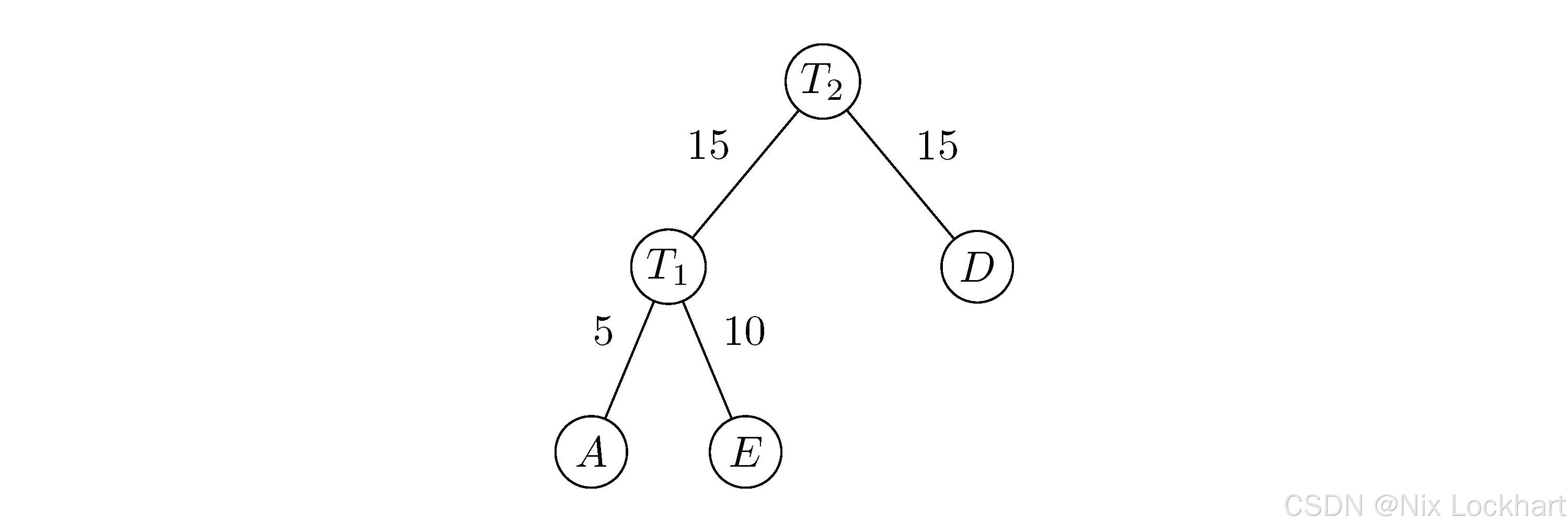
图5：构造二叉树2

然后我们从集合FFF中删除二叉树T1T_{1}T1和TDT_DTD，并将新构造的二叉树T2T_{2}T2加入集合FFF，此时有：

F={T2(30),TC(30),TB(40)}F=\{T_{2}(30), T_C(30), T_B(40)\}F={T2(30),TC(30),TB(40)}

继续选取权值最小的两棵二叉树T2T_{2}T2和TCT_CTC，构造一棵新的二叉树T3T_{3}T3，其根结点的权值为30+30=6030+30=6030+30=60，左子树为T2T_{2}T2，右子树为TCT_CTC，如下图所示：

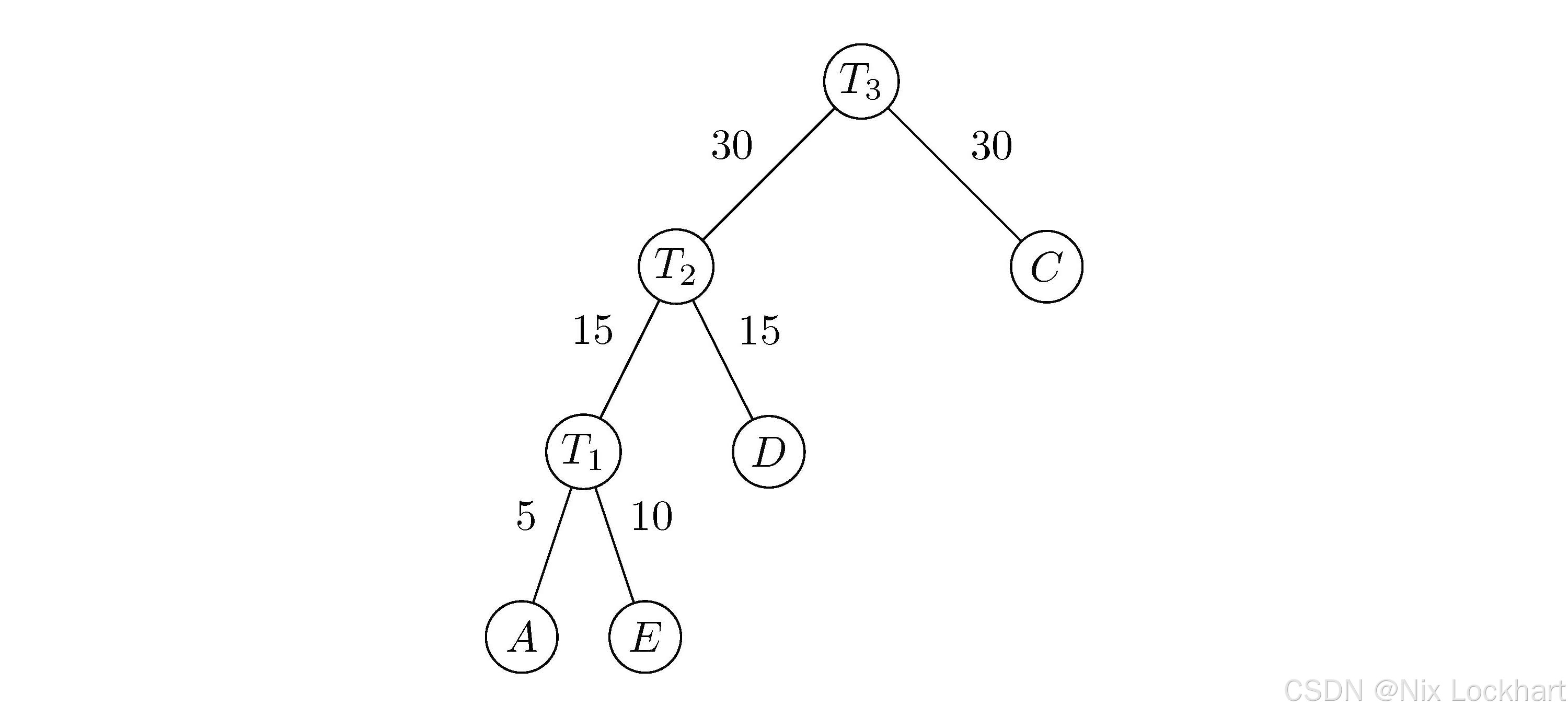
图6：构造二叉树3

同样我们从集合FFF中删除二叉树T2T_{2}T2和TCT_CTC，并将新构造的二叉树T3T_{3}T3加入集合FFF，此时：

F={TB(40),T3(60)}F=\{T_B(40), T_{3}(60)\}F={TB(40),T3(60)}

最后，我们选取权值最小的两棵二叉树TBT_{B}TB和T3T_3T3，构造一棵新的二叉树TTT，其根结点的权值为40+60=10040+60=10040+60=100，左子树为TBT_{B}TB，右子树为T3T_3T3，如下图所示：

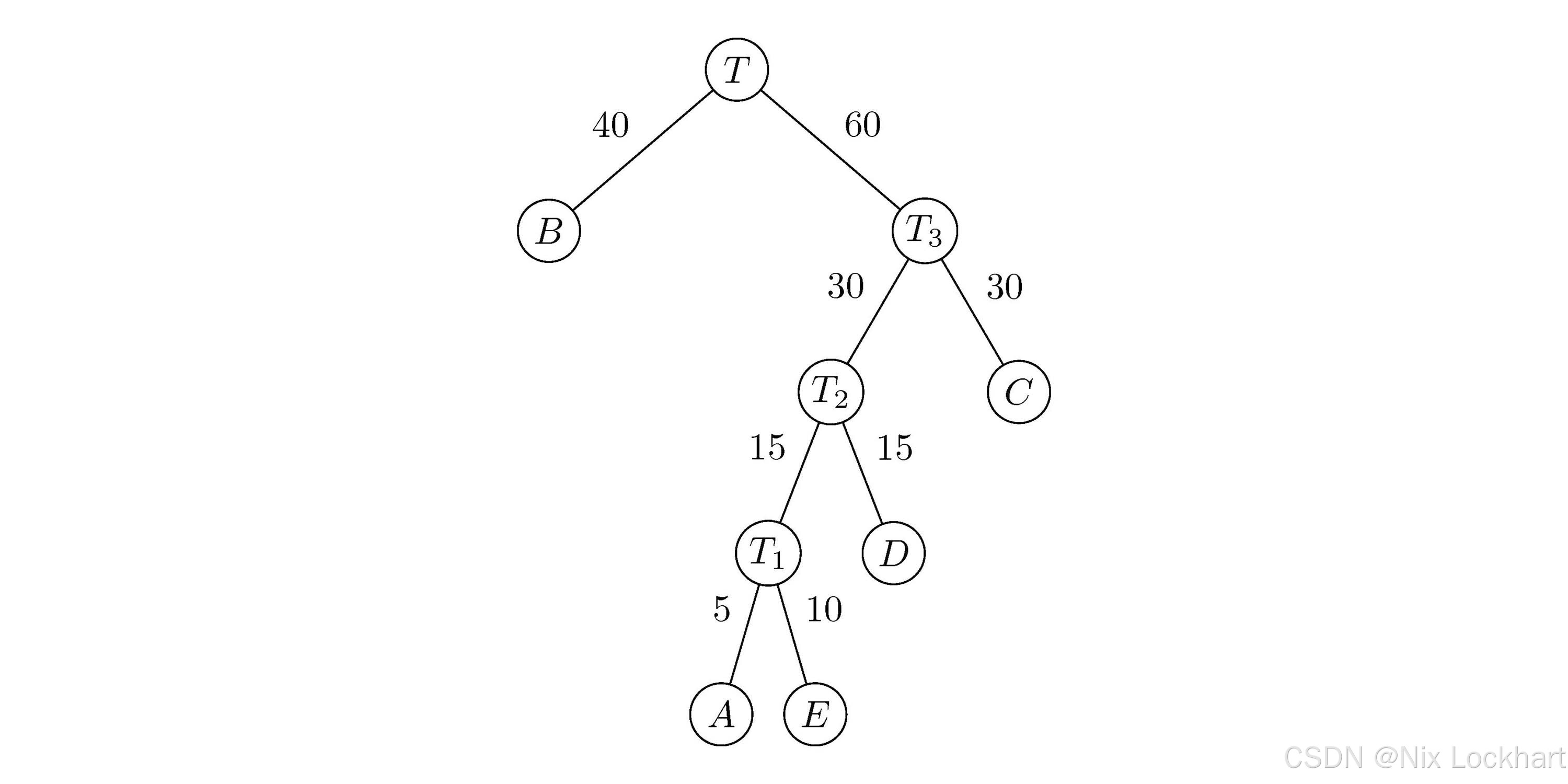
图7：构造二叉树4

此时集合FFF中只剩下一棵二叉树TTT，这棵二叉树即为所求的哈夫曼树。

可以看到，与我们之前构造的那棵二叉树是不一样的，那它的表现如何呢？我们来计算一下它的带权路径长度：
40×1+30×2+15×3+5×4+10×4=20540 \times 1 + 30 \times 2 + 15 \times 3 + 5 \times 4 + 10 \times 4 = 20540×1+30×2+15×3+5×4+10×4=205

可以看到，它的带权路径长度比我们之前构造的二叉树(225)还要小，说明使用哈夫曼树构造的二叉树更优。

不过现实情况总是复杂的，我们将上图中的哈夫曼树转化为实际代码如下：

if (score >= 80 && score < 90)
	printf("良好\n");
else if (score >= 70 && score < 80)
	printf("中等\n");
else if (score >= 60 && score < 70)
	printf("及格\n");
else if (score >= 90)
	printf("优秀\n");
else
	printf("不及格\n");

可以看到，前三个判断条件每条都要进行两次比较，而最后两个判断条件每条只要进行一次比较。这样一来，在实际应用中，反倒不一定会有我们之前构造的那棵树高效，不过这无所谓，因为我们学习哈夫曼树的目的并不是为了优化程序的执行效率，而是为了接下来的这个用途。

3、哈夫曼编码

现如今，网络带宽虽越来越大，但数据量也在成倍增长，数据压缩依然是一个重要课题。而哈夫曼研究出这种二叉树的初衷，正是为了数据压缩。

比如，我们有一段文本："BADCAFEFEE"，要通过网络传输，若使用我们在串中提到的ASCII编码，每个字符用8位二进制表示，则总共需要10×8=80位，这太夸张了；我们发现，文本中只出现了6个字符A、B、C、D、E、F，那我们只用3位二进制就能完全表示它们了，如下表所示：

字符	A	B	C	D	E	F
编码	000	001	010	011	100	101

如此一来，我们传输的内容就成了"001000011010000101100101100100"这样传输同样的文本只需要10×3=30位，节省了整整50位，但实际上，当我们需要传输一篇较长的文章时，对应的二进制串依旧十分可怕。但我们都知道，日常生活中，我们使用各个文字的频率是不同的，如英文中常出现字母A、E、I、O、T等，而字母Q、X、Z等则很少出现。

我们就以假设文本中每个字母出现的频率如下：

字符	A	B	C	D	E	F
频率(%)	27	8	15	15	30	5

这样一来，我们有了频率数据，就可以构造哈夫曼树了：

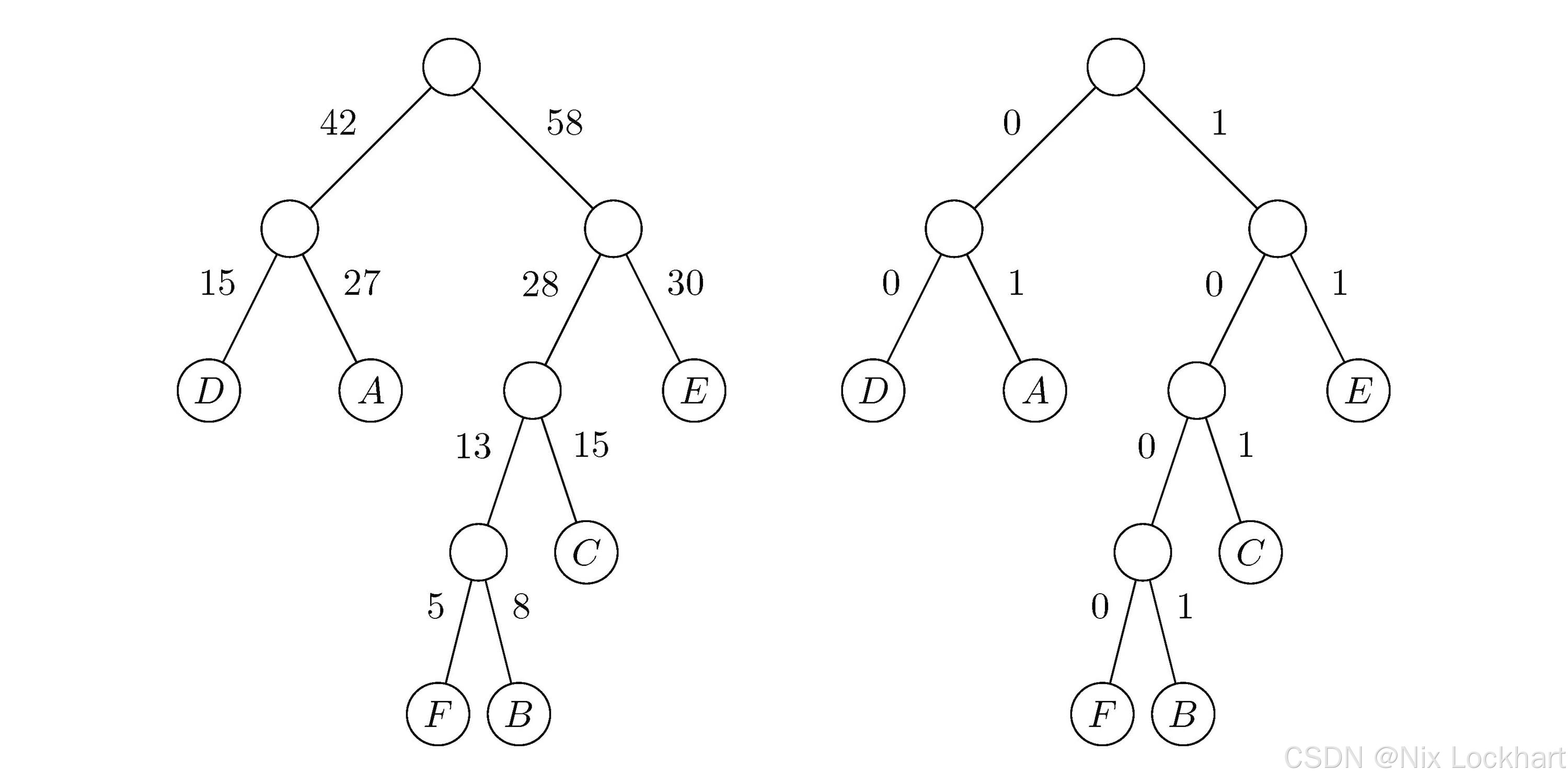
图8：哈夫曼树

我们可以看到，左图中的树就是我们通过频率数据构造的哈夫曼树，而右图中的树则是我们将左分支权值改为0，右分支权值改为1后的二进制树。

一般地，设需要编码的字符集{c1,c2,⋯ ,cn}\{c_1,c_2,\cdots ,c_n\}{c1,c2,⋯,cn}，各个字符在文中出现的次数/频率(权值)为{w1,w2,⋯ ,wn}\{ w_1, w_2,\cdots ,w_n \}{w1,w2,⋯,wn}，以w1w_1w1、w2w_2w2、⋯\cdots⋯、wnw_nwn为相应叶子结点的权值来构造一棵哈夫曼树。规定其左分支代表0，右分支代表1，则从根结点到叶子结点的路径上所经过的0和1就构成了该叶子结点(字符)的哈夫曼编码(Huffman Code)。

这样，我们对这6个字母用其从根结点到其叶子结点的路径来进行编码，可以得到下表所示的二进制编码：

字符	A	B	C	D	E	F
编码	01	1001	101	00	11	1000

我们再对应的文本"BADCAFEFEE"进行编码，得到："100101001010110001110001111"，只有27位，节省了3位，但随着文本内容量的增大，这种压缩的优势会显现出来。

编码的问题解决了，我们该如何解码呢？如果我们收到的是上述三位二进制编码，我们只需要三位一译即可，但是我们发现通过哈夫曼树构造出的编码并不是定长的，而是变长的，这样一来，我们就没法三位一译了。那我们该如何解码呢？它会出现歧义吗？

要设计长短不等的编码，必须保证任意字符的编码都不是另一字符编码的前缀 ，这种编码称为前缀编码(Prefix Code)，而哈夫曼编码正是一种前缀编码。

仔细观察就会发现，我们在上表中的编码中，不存在某个编码是另一编码的前缀的情况，比如A的编码是"01"，没有其他编码是以"01"开头的，所以我们可以放心大胆地进行解码。

当然，我们作为接收方在解码前肯定需要与发送方沟通约定好哈夫曼编码规则的，否则我们根本无法解码。假设我们已经知道了上表中的编码规则，我们来看看如何解码。

现在我们收到编码"100101001010110001110001111"和上表中的编码规则，我们从左到右依次读取二进制位：首先是1001，我们知道它对应B，然后是01，对应A，如图9，其余同上，最终我们会得到"BADCAFEFEE"，完成解码。

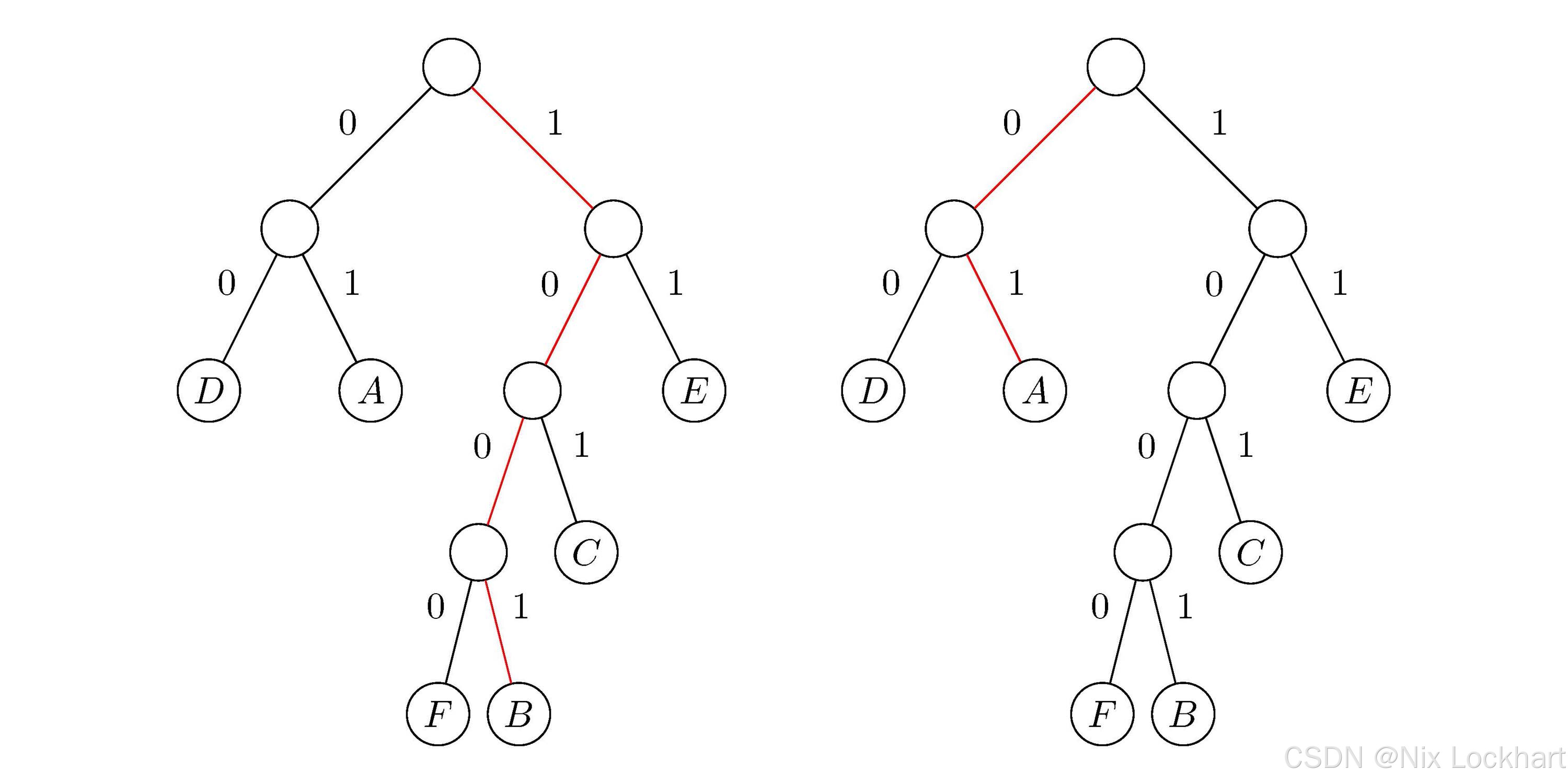
图9：哈夫曼编码解码过程

二、本章总结回顾

至此，"树"这一一对多的数据结构的学习便结束了。我们了解到树(Tree)是由n(n≥0)n(n≥0)n(n≥0)个结点的有限集 ，它是一种"一对多"的非线性数据结构，用以解决更为复杂的实际问题。我们学习了树的递归定义，认识了根、子树、度、高度/深度 等一系列重要概念。之后，我们重点研究了树的三种存储结构------双亲表示法、孩子表示法、孩子兄弟表示法，并发现孩子兄弟表示法能巧妙地将任意树转化为结构固定的二叉树。

在此基础上，我们深入学习了二叉树 ，包括其五种基本形态、满二叉树与完全二叉树等特殊形式，并掌握了其重要的五大性质 。我们探讨了二叉树的顺序和链式存储，并详细学习了先序、中序、后序 三种遍历方法，理解了如何通过递归遍历实现二叉树的创建与序列推导。为了利用闲置指针并方便查找前驱后继，我们还学习了线索二叉树 。最后，我们了解了哈夫曼树及其在数据压缩领域的经典应用------哈夫曼编码 ，体会到了带权路径长度最短的精妙之处。