一、概念
1.什么是最优化?
达成目标的最优方案
2.最优化的发展
3.最优化的特点
计算机结合,适用范围广,联系实际
4.生活中的最优化
5.最优化数学模型
目标函数
决策变量
约束条件
6.最优化方法复杂性
评价指标:时间空间复杂性,执行的次数,占用的存储空间
7.最优化分类
大致看一下,目标函数:线性、非线性
二、最优化数学基础
1.线性代数
(1)范数
范数概念
常用向量范数
向量的lp范数:
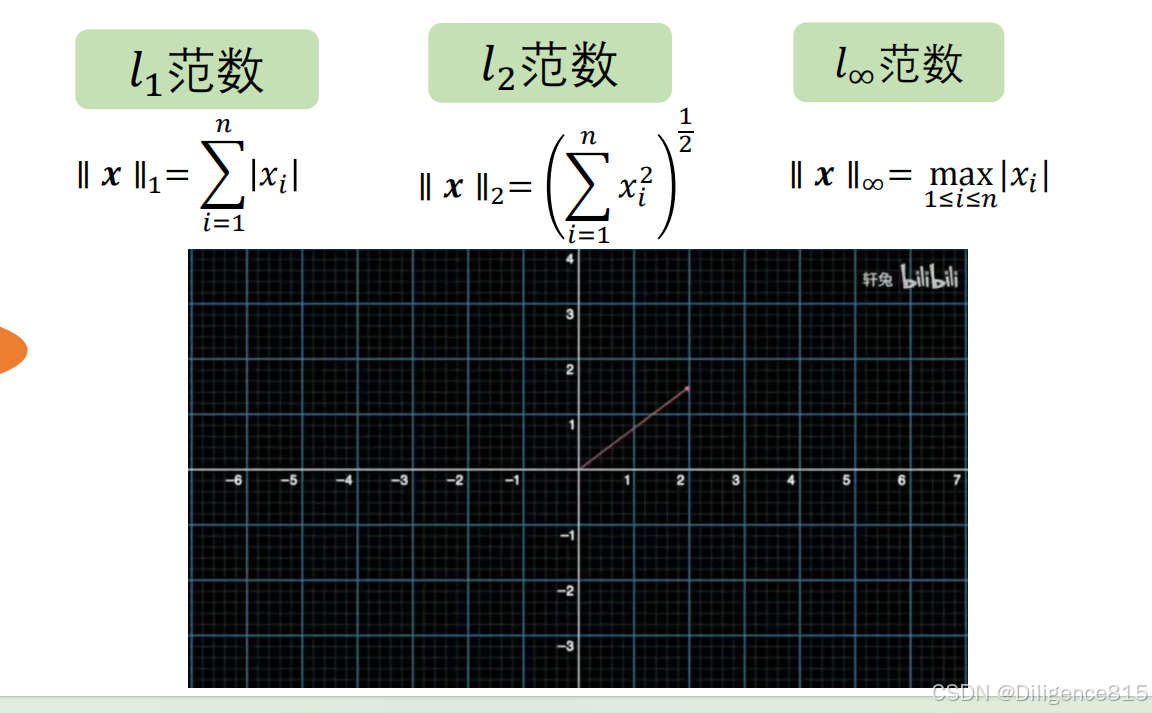
等价向量范数
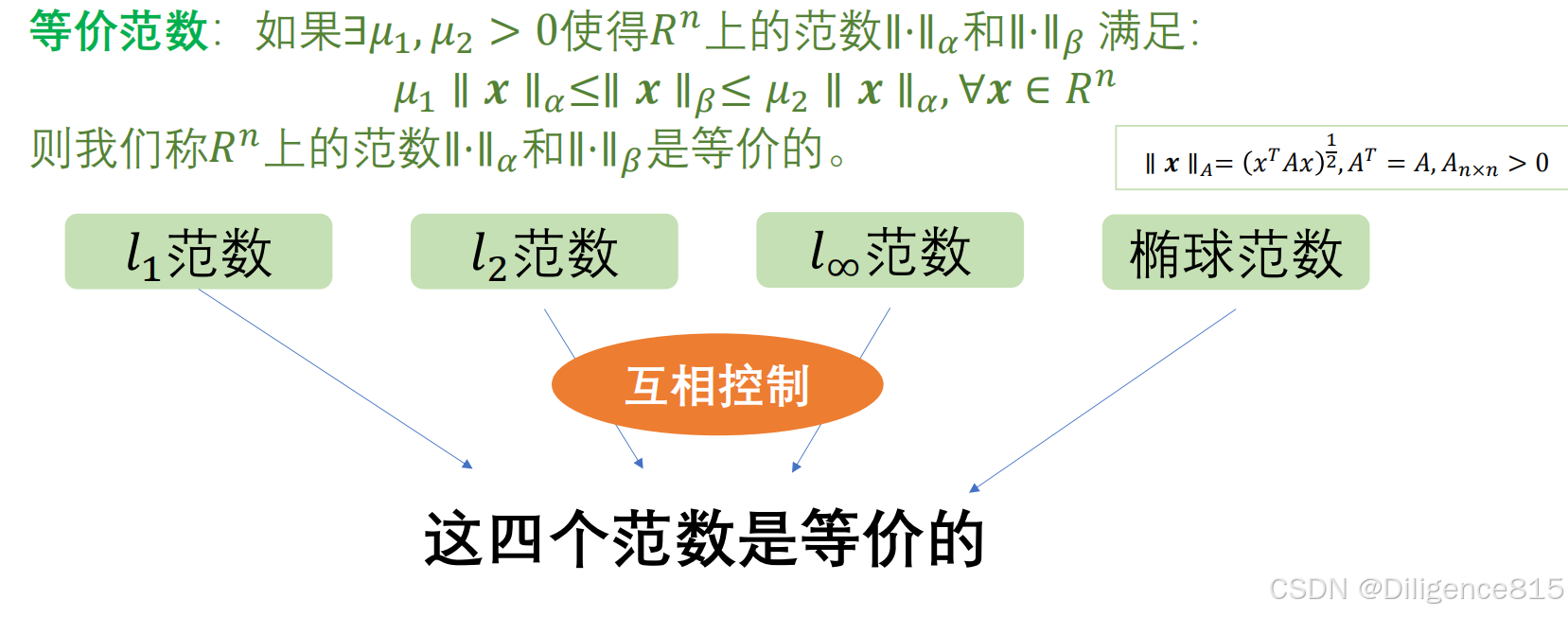
一范数和无穷范数的等价性。
向量范数不等式:不考
矩阵范数
(2)矩阵:看一下,小题
矩阵的阶
矩阵的转置T
矩阵的秩r
矩阵的迹Tr,主对角线元素之和,特征值之和
矩阵的逆
矩阵的行列式det
矩阵的特征值Ax=ax
2.微积分:梯度
连续
导数


可微可导
差商
3.凸分析 :如何判断是否为凸函数?
凸集
凸函数
凸集的分离与支撑
三、特殊情形------Linear Programming,LP 线性规划
是最优化问题的特殊情形,实质是选出一组变量作为解,使得其满足一组确定的线性式 (约束条件)条件下,让一个线性函数(目标函数)达到最优。
根据目标函数,可分为最大化问题与最小化问题;根据决策变量的线性表达式和常数项之间的连接符,可分为大于等于约束、等于约束、小于等于约束。
一般形式是什么?
其标准形表示形式如下:
目标函数要取得最小值
线性约束均为等式约束
所有决策变量都要满足非负约束
注意,这种转换必须是"等效"的,即转化后问题的最优解一定能通过某种方式推出原问题的最优解
简化形式:
向量形式:
矩阵形式:
集合形式:
非标准形如何转化为标准形?
(1)目标函数是最大化,而不是最小化
将原问题的目标函数乘以(-1),变换后最优解不变
令
可化为
(2)线性约束中有大于等于约束,有小于等于约束。
引入松弛变量,剩余变量进行转换
大于等于约束
在约束条件左边减去 非负松弛条件变量
小于等于约束
在约束条件左边加上非负松弛条件变量
(3)决策变量无约束,我们称之为自由变量
消除自由变量,引入两个非负变量
假设无约束,可化为标准形,令
(4)目标函数含有绝对值项,消除绝对值符号


已知标准线性规划问题,如何求解?
可行解 :满足所有约束条件的解 称为线性规划问题的 可行解
可行域 :所有可行解构成的集合称为问题的 可行域 ,记为 R
最优解 :使目标函数达到最小值的可行解叫 最优解
基、基向量、基变量、非基向量、非基变量:
设约束方程的系数矩阵 A 中,有 m 个线性无关的列向量记为 B = ( p 1 , p 2 ,..., p m ),则 B为该
线性规划的一个 基 ,向量 p 1 , p 2 ,..., p m 称 为 基向量;与之对应的变量x1,x2,...,xm称为
基变量 ,记为 ; 其余的向量为 非基向量 ,记为 N = ( p m +1 , p m +2 ,..., p n);
其余的变量为 非基变量 ,记为
矩阵形式可化为:
令自由未知数(非基变量)为0,得
中各向量线性无关,故存在唯一解
故唯一解为,也是此方程对应于基底B的一个基本解
基本可行解 :解出的基本解,有一部分满足变量的非负约束,即解大于等于0,这些解称为基本可行解;
有些解小于0的,显然不满足大于等于0的条件,这些基解不是可行解,没有用处;
可行基 :基本可行解对应的基,称为 可行基;
退化的基本可行解 :若基本可行解中有一个或多于一个基变量取值为零时,该解为 退化的基本可行解;
否则,为 非退化的基本可行解。
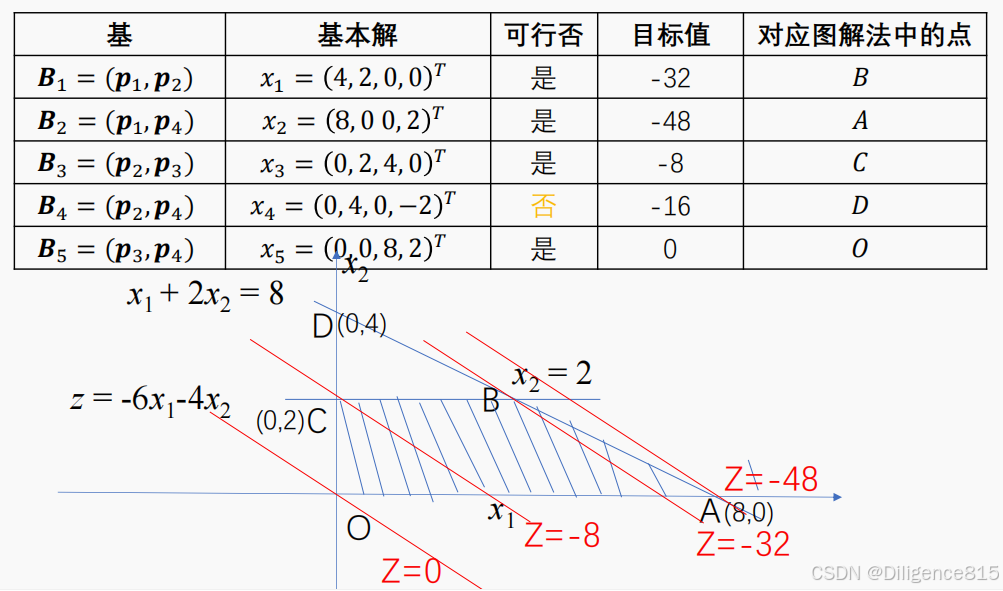
a.图解法


注意:图解法不要求化为标准形
b.一般求解步骤



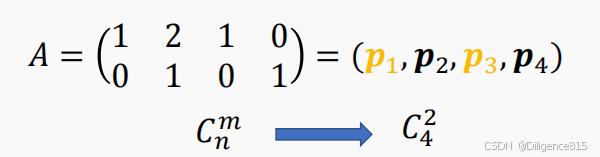
c.MATLAB解法



2.线性规划单纯形法
①基本原理
1中所用方法本质上,是一种枚举法,适用于小型规划问题(阶数m ≤6和维数n≤5的情况)
单纯形法适用于大型规划问题,其基本思想如下:
有选择地取(而不是枚举所有的)基本可行解,即是从可行域的一个顶点出发,沿着可行域的边界移到另一个相邻的顶点,要求新顶点的目标函数值不比原目标函数值差,如此迭代,直至
找到最优解,或判定问题无界。
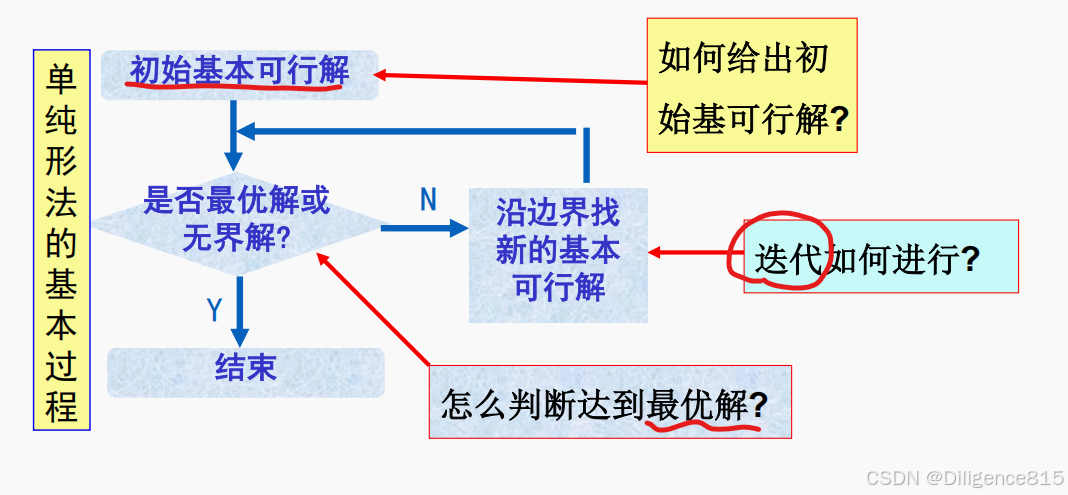
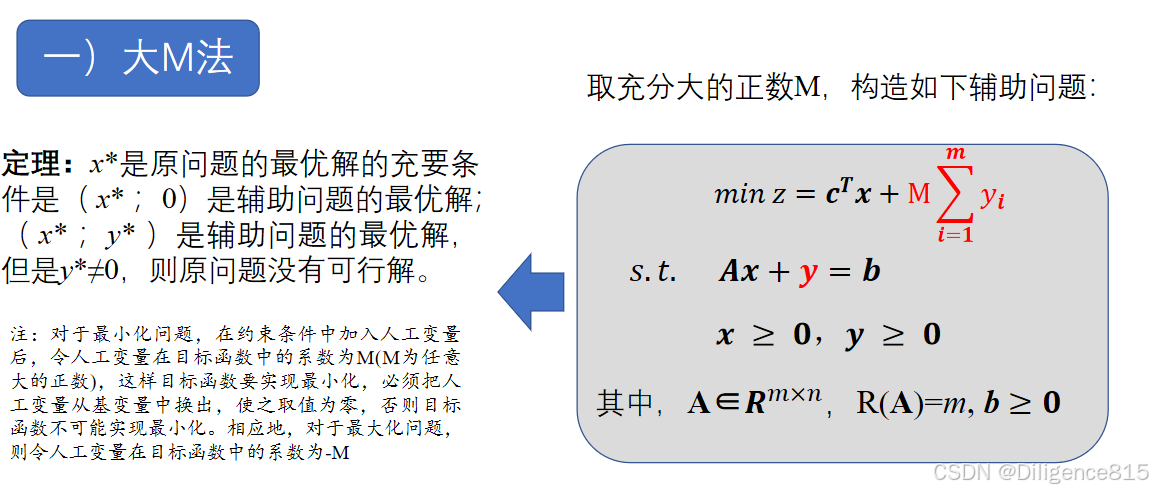
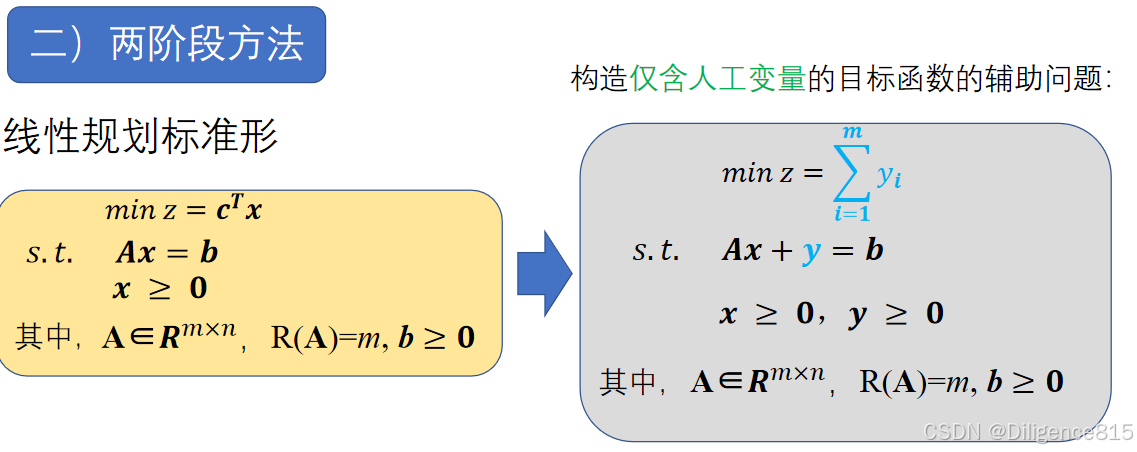
②如何给出初始基可行解?------矩阵运算 或者 手算法,具体可见习题,大M法,两阶段法

③怎么判断达到最优解?------定理二
④如何迭代?------定理四,满足最小比值原则

先找出基本可行解



表格形式
和公式法类似,但方便了计算
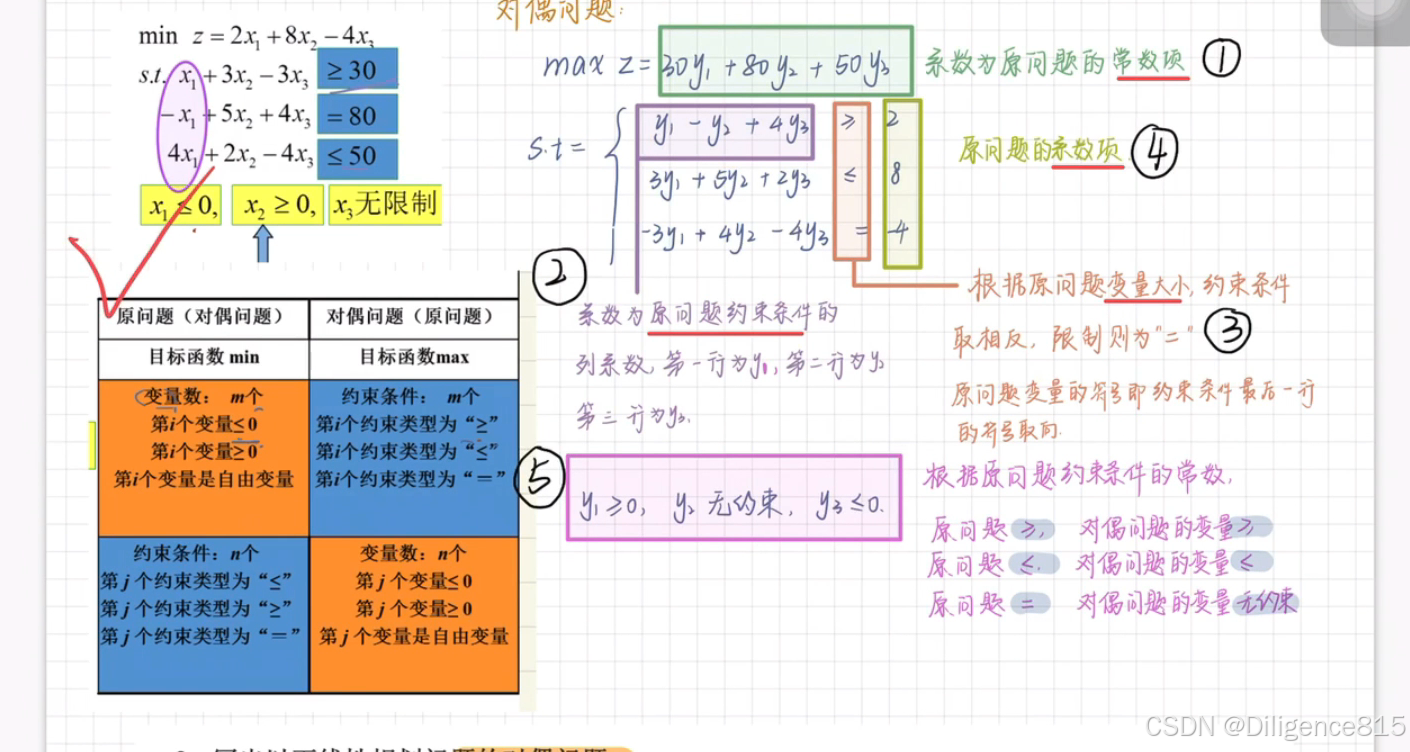
3.线性规划对偶问题
任一线性规划问题都存在另一与之伴随的线性规划问题,它们组成一对互为对偶的线性规划问题 线性规划的对偶问题与原问题互为对偶,线性规划的原问题与对偶问题地位具有对称关系
套模板,具体情况具体分析
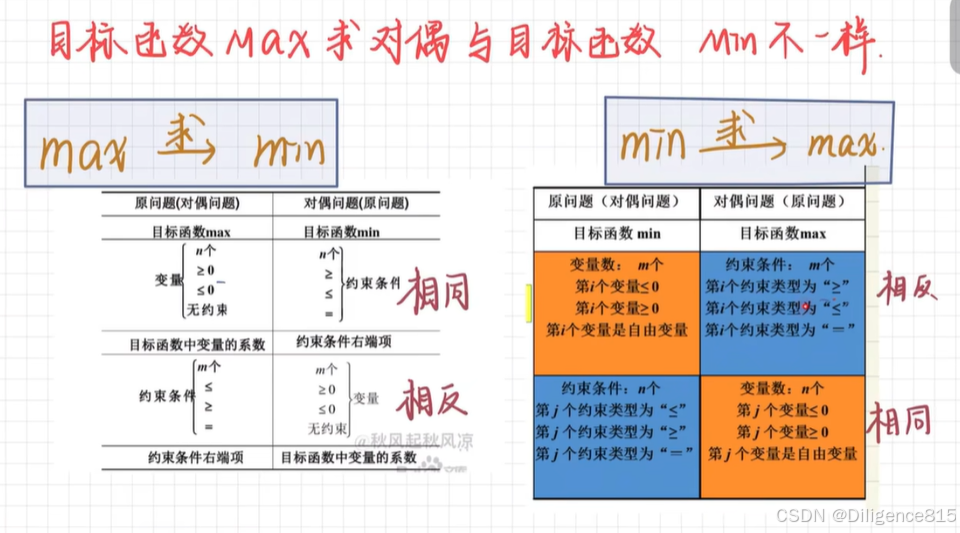
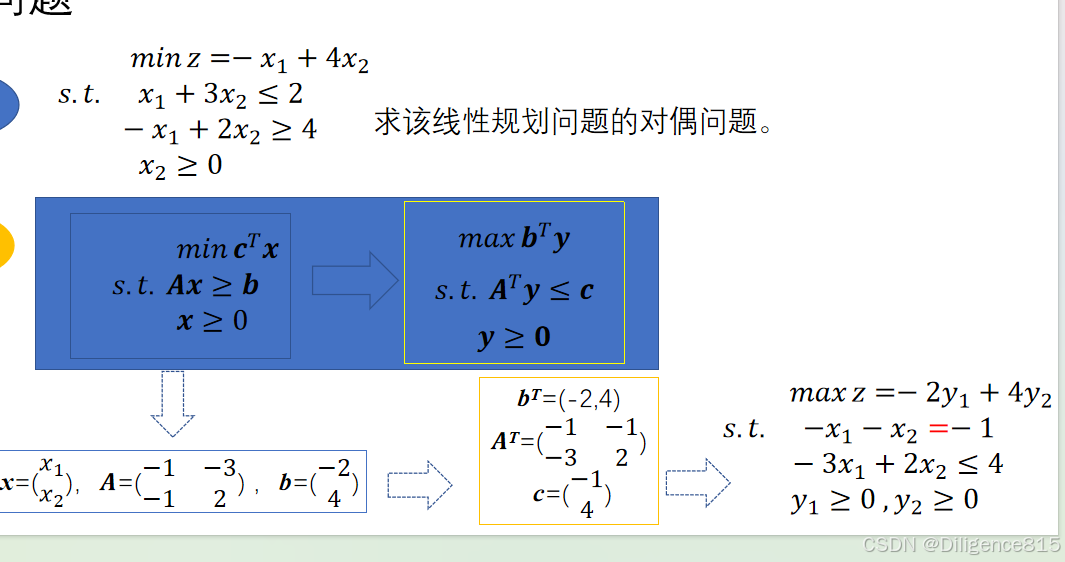
和一堆相关定理,额,要晕了。不想看,来不及了啊啊啊
四、非线性规划问题
目标函数或者约束条件,只要有一个是非线性的,就叫做非线性规划问题。
常见情况是解析解求不出来或者非常困难,求的是数值解。
1.无约束优化问题
问题形式是什么?
**怎么求解?**迭代法,不断求解点列,直至收敛


a.直接法:只要用到目标函数值,不需要求导数

b.间接法:计算时需要用到目标函数的导数

①信赖域方法:方向与步长合二为一,,在一个小的邻域内求
②线搜索方法:已知方向 ,求步长
一阶精确线搜索法:要计算大量梯度及导数值

一阶非精确线搜索法:

6.梯度法/最速下降法

7.共轭梯度法
不考
2.约束优化问题
问题模型是什么?
如何求解?
(1)直接法:可行域直接求解目标函数最优解,初始点、迭代方向、步长,同时保证可行性

直接搜索法:对约束优化问题不预先做转换,对目标函数导数的存在无要求;随机方向、约束坐标轮换、复合形法
可行方向法:可行点,迭代,得到新的可行点;转化为无约束了

(2)间接法:约束优化转化为无约束优化,可求解等式加不等式约束

序列二次规划:用二次函数逼近目标函数;SLP,SQP

惩罚函数法:序列无约束优化,构造增广目标函数,将约束问题转化为无约束问题;
要达到什么目标------其最优性条件是什么?
对于等式约束:引入拉格朗日乘子,满足微分条件=0的点即为局部最优解
对于不等式约束:KT条件
一般的约束问题 :KKT条件,最优解的**必要条件,**对于凸规划问题就是充要条件了
KKT的推导:
先不考虑非等式约束,求其最优条件
代入,可能有
①不满足,应舍弃,那新的解在哪里呢?
②正好满足,但是此时约束没起作用!为无约束求解问题,此时
③转化为等式约束,引入拉格朗日乘子
将②③统一形式,两者必有一为0
KKT的应用:
等式求最优,不等式验证
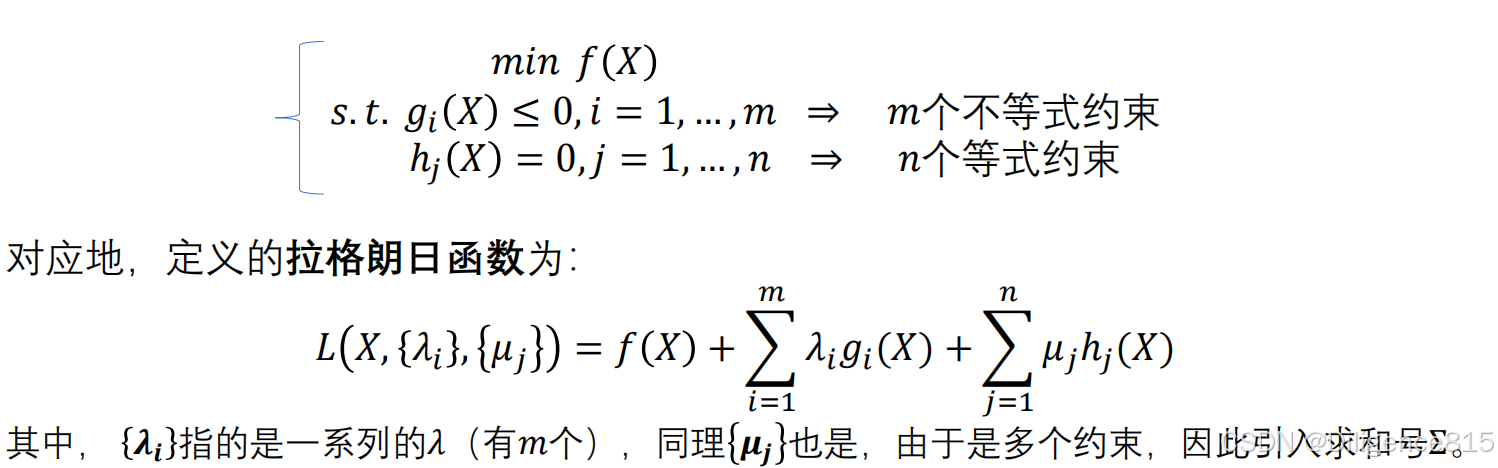
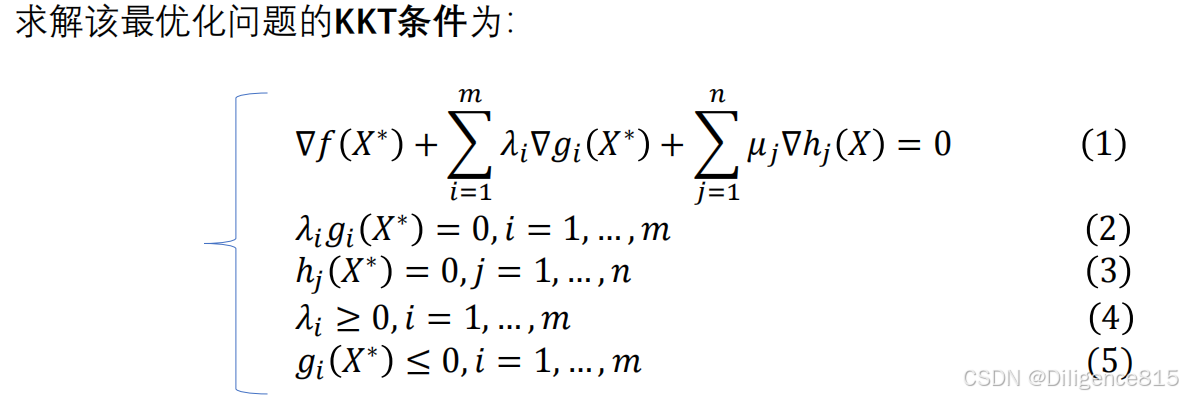
求KKT点并验证的典型例子:
约束优化算法------惩罚函数法
加入惩罚函数,将问题转化为一个无约束优化问题
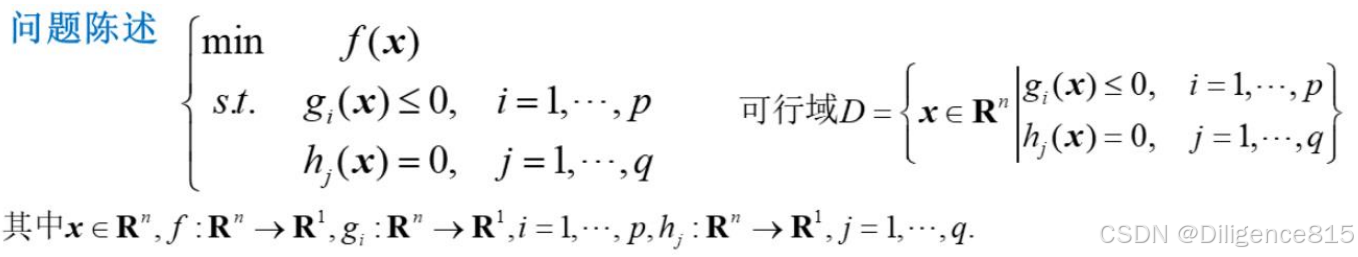
外点法/罚函数:出界,罚
小于或等于对应max
构造增广的目标函数,加入惩罚函数
问题转化为
之后再用某种无约束优化算法求解
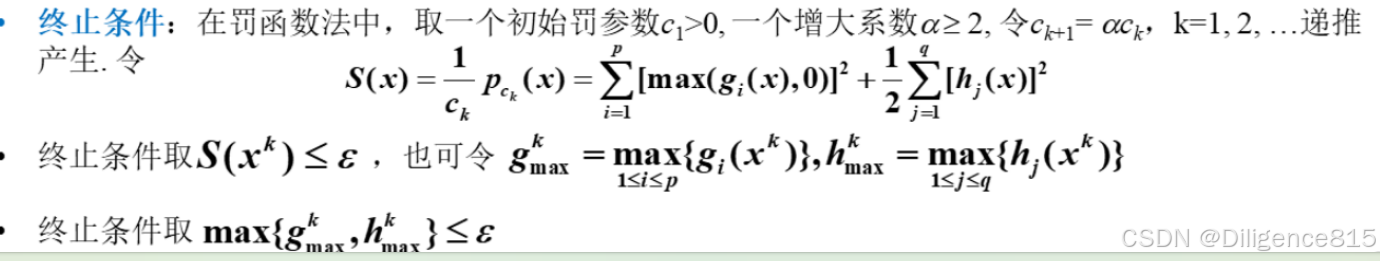
内点法/障碍函数法:仅不等约束,从可行域内部趋于边界

乘子法
六、多目标优化问题
1.多目标规划概念
同时存在多个最大化或最小化的目标函数,并且目标函数之间并不是相互独立的,也不是相互和谐融洽的,或多或少会存在冲突,使其不能同时满足所有的目标函数。
由于存在冲突,只能使多个子目标尽可能地都达到最优化。
解非唯一,存在一组由众多 Pareto最优解组成的最优解集合 ,集合中的各个元素称为 Pareto最优解或非劣最优解
都有可能是不存在的
2.多目标规划典型实例
同时达到最优举例。工厂
3.多目标规划求解方法
目标规范化:归一化
绝对最优解:一般不存在,是所有优化目标的公共解
解集:
4.求解
约束法:确定主要目标,转换为单目标
评价函数法:h(F(x)),F(x)为原多目标函数
理想点:分别计算最优解集合,找最接近的。最短距离理想点
加权法:分别求下界
其实就是最优化求解的问题,给你一些方法,感觉偏理论,对实际应用涉及较少