文章目录
什么是递归? 函数自己调用自己。
为什么会用到递归?本质:在处理主问题时,需要解决子问题,两者的处理方式完全一致。
问题 -> 相同的子问题 -> 相同的子子问题......
直到子问题不能继续拆分
从宏观角度看待递归!1.不要在意递归的细节展开图 --- 写完代码不要再去纠结递归展开图;
2.把递归函数当成一个黑盒 --- 赋予这个黑盒一个任务;
3.相信这个黑盒一定能帮助我们完成这个任务。
如何写好一个递归:1.先找到相同的子问题 -> 确定函数的功能以及函数头的设计;
2.只关心某一个子问题是如何解决的 -> 函数体
3.不能继续拆分的子问题 -> 递归出口
汉诺塔问题
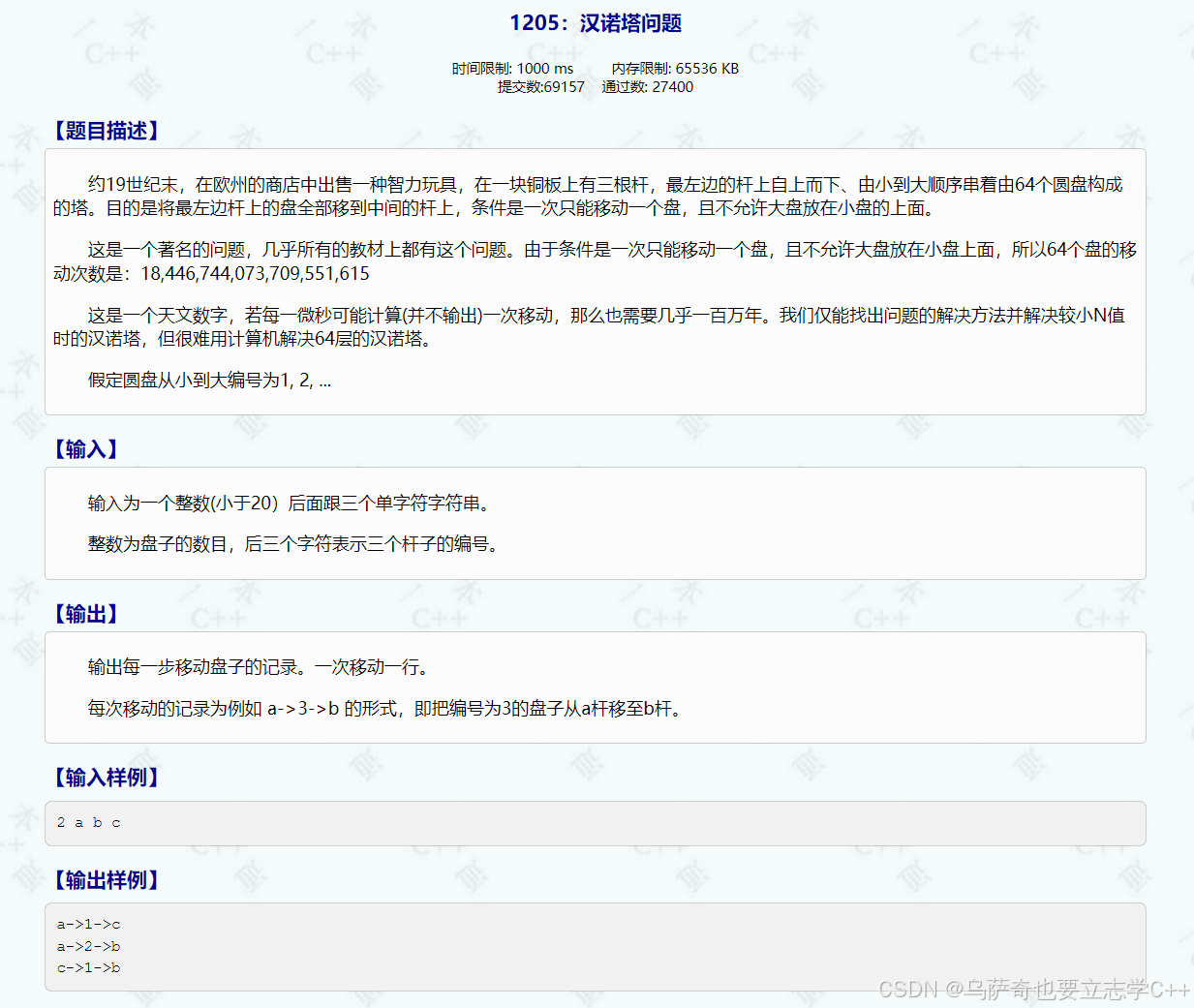
题目描述
题目解析
注意,本题是逻辑推导,不需要用真实的数组记录每个杆上的盘子状态,因为汉诺塔的递归解法是 "逻辑上的步骤推导",而非 "物理上的状态模拟"------
它不需要数组记录每个杆的盘子,因为递归的分层任务本身就严格遵循规则,每一步移动都是确定且合法的。
要将a杆的盘全部移到b杆,根据规则要先将a杆最下面的盘移到b杆最下面,再将剩余的盘依规则移到b杆。
我们先以a杆上有三个盘为例,首先借助b杆将a杆的上面两个盘移到c杆,然后将a杆的底盘移到b杆,然后借助a杆将c杆的两个盘移到b杆,所以不论有多少个盘,我们都可以依据这个思路写出本题的递归代码。
代码
cpp
#include <iostream>
using namespace std;
// 把x杆的n个盘子借助y杆全部转移到z杆上
void dfs(int n, char x, char y, char z)
{
if (n == 0)
return;
dfs(n - 1, x, z, y);
printf("%c->%d->%c\n", x, n, z);
dfs(n - 1, y, x, z);
}
int main()
{
int n;
char a, b, c;
cin >> n >> a >> b >> c;
dfs(n, a, c, b);
return 0;
}占卜DIY
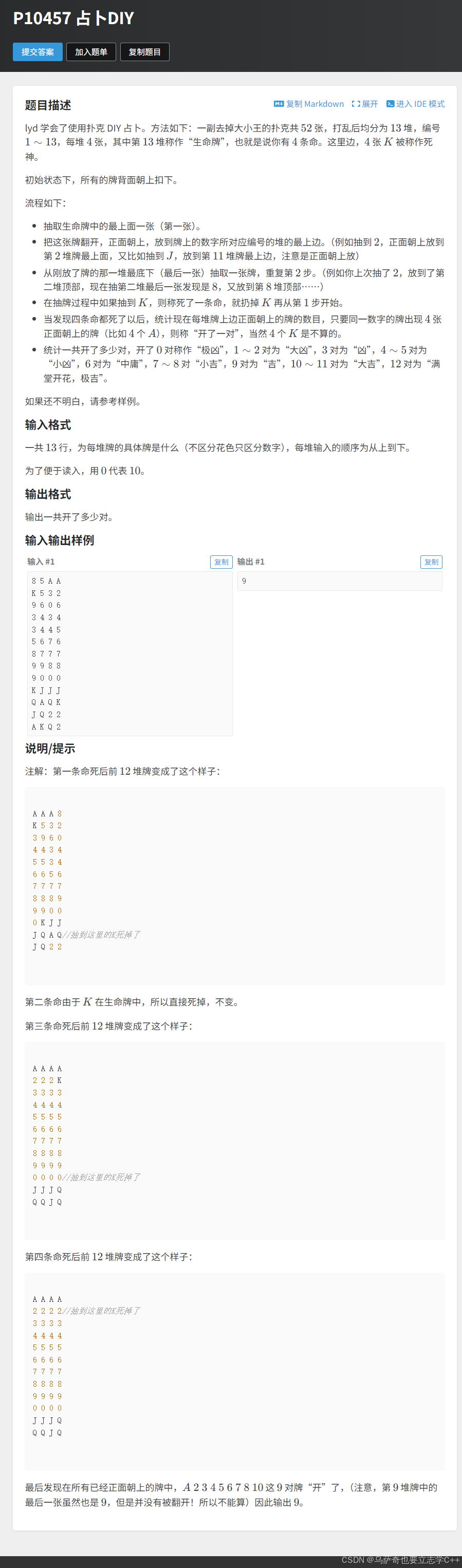
题目描述
题目解析
补充一个小tip:
cpp
// 输入:5 5
int x;
char y;
cin >> x >> y;首先明确,计算机中所有数据最终都是以 ASCII 码(整数) 形式存储的
输入 5 5 后,变量x和y存储的值是不一样的
整型变量 x 存储的值是:5(数字 5)
字符型变量 y 存储的值是:'5'(字符 5,ASCII码为53)
本题是一道模拟题,我们可以用模拟题的思路解决,由于本题有重复子问题,所以我们来尝试用递归解决。首先本题需要一个二维数组存储输入数据,处理输入是一个难点,因为输出含a j q等字符,所以需要用char类型变量存放输入,再把字符变量转化为整型变量存进二维数组里。
然后本题的模拟逻辑是可以简化的,如果按照题意写拿牌,插入牌的代码是比较难实现的,我们可以用一个巧妙的方法,创建一个cnt数组,cnt[i]表示第i堆牌还有多少张牌没被翻的牌,所以cnt[i]会被初始化为4,而cnt[i]的值又刚好是这堆牌最后一张没被翻的牌的下标,所以拿一张牌x,把牌x放在x堆的最上面,然后把x堆的最下面的一张牌拿出来的操作就可以简化成拿一张牌x,直接拿x堆的最下面的一张牌,然后cnt[x]--。
有了上面的方法论,那么本题的递归代码就很好实现了,子流程就是拿到一张牌x,找到堆x:a[x],拿出堆x最后一张没有被翻开的牌t:a[x][cnt[x]],然后cnt[x]--,最后继续拿着t进行递归,当摸到k就递归返回。
最后统计有多少种牌四张全部正面朝上,也就是统计有多少堆牌四张全被翻开了,当cnt[i]等于0就说明第i堆牌四张全被翻开了。
注意递归出口不用判断cnt[x]是否==0,因为本题每种牌只有4张,cnt[x]==0是递归的隐性终止条件,此时该堆无牌可翻,递归自然终止。
代码
cpp
#include <iostream>
#include <vector>
using namespace std;
//存放13堆牌
int a[14][5];
//cnt[i]表示第i堆牌还有多少张没被翻的牌,也是第i堆牌中待被翻的牌的下标
int cnt[14];
void dfs(int x)
{
//遇到k直接退出
if (x == 13 )
return;
int t = a[x][cnt[x]];
cnt[x]--;
dfs(t);
}
int main()
{
//初始化13堆牌
char x = 0;
for (int i = 1; i <= 13; i++)
{
cnt[i] = 4; //初始化cnt数组
for (int j = 1; j <= 4; j++)
{
cin >> x;
if (x >= '2' && x <= '9')
{
a[i][j] = x - '0';
}
else if(x == '0')
a[i][j] = 10;
else if (x == 'A')
a[i][j] = 1;
else if (x == 'J')
a[i][j] = 11;
else if (x == 'Q')
a[i][j] = 12;
else
a[i][j] = 13;
}
}
//开始占卜
for (int i = 1; i <= 4; i++)
{
//依次抽取第13堆牌
dfs(a[13][i]);
}
//输出结果
int ret = 0;
for (int i = 1; i <= 13; i++)
{
if (cnt[i] == 0)
ret++;
}
cout << ret << endl;
return 0;
}FBI树
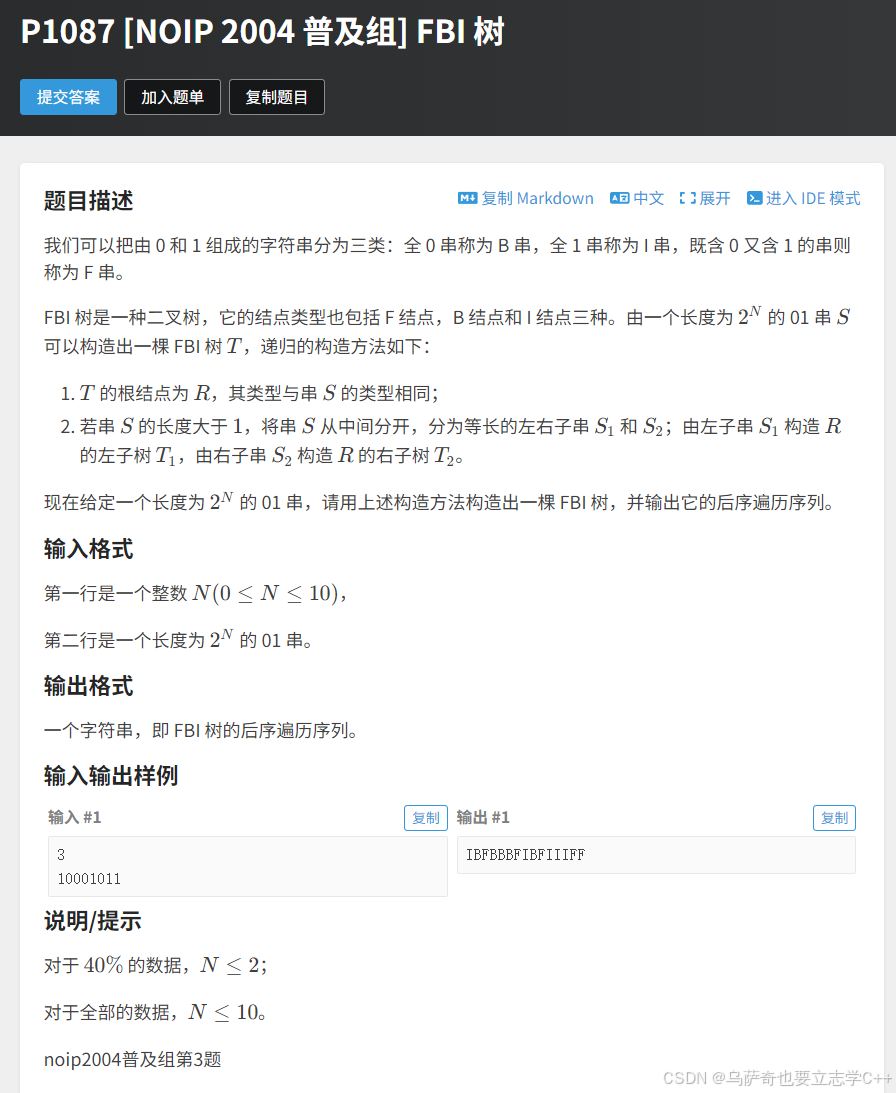
题目描述
题目解析
本题构造+遍历树本质也是重复子问题,所以我们也尝试用递归来解决。
1、判断子串类型我们会先想到遍历整个子串,检查字符串中字符0和字符1的出现情况,这种方法是可以解决问题的。但是还有一种更优的做法,利用前缀和整型数组f预处理输入的01字符串,当我们拿到一个区间[left,right],我们先算出[left,right]的区间和,也就是f[right] - f[left - 1],然后判断区间和和right - left之间的关系,如果区间和等于right - left + 1,说明区间全为1,那么当前字符串类型就是I,如果区间和等于0,说明区间全为0,那么当前字符串类型就是B,否则就是F。
2、本题只给了2的x次方,我们需要将x转化为具体值,这里可以运用右移运算符,2的x次方等于1 << x。
3、本题递归出口需要额外注意,当left > right直接退出,当left == right时是叶子结点,不能直接退出,还需要输出当前结点类型,但是不能继续递归处理,我们以[2,2]为例,如果继续递归处理就会递归左区间[2,2]和递归右区间[3,2],当递归左右区间返回后还会再输出一次当前区间的结点类型,就相当于一个区间输出了两次,要解决这个问题我们需要在递归左右区间时加一个判断,当left == right时直接输出当前结点类型并返回。
代码
cpp
#include <iostream>
using namespace std;
const int N = 11;
int n;
int f[1 << N]; //前缀和数组
void dfs(int left, int right)
{
if (left > right)
return;
//判断当前字符串类型
char root;
int num = f[right] - f[left - 1];
if (num == right - left + 1)
{
root = 'I';
}
else if (num == 0)
{
root = 'B';
}
else
{
root = 'F';
}
if (left == right)
{
cout << root;
return;
}
int mid = (left + right) / 2;
dfs(left, mid);
dfs(mid + 1, right);
cout << root;
}
int main()
{
cin >> n;
n = (1 << n);
//处理输入 + 初始化前缀和数组
for (int i = 1; i <= n; i++)
{
char ch;
cin >> ch;
int t = 0; //用来标记输入字符是否为1
if (ch == '1')
t = 1;
f[i] = f[i - 1] + t;
}
//利用递归构建树并输出后序遍历结果
dfs(1, n);
return 0;
}以上就是小编分享的全部内容了,如果觉得不错还请留下免费的关注和收藏如果有建议欢迎通过评论区或私信留言,感谢您的大力支持。
一键三连好运连连哦~~
