数据结构：树

树的概念：

树是一种非线性的数据结构，由节点（Node）和边（Edge）组成。树的结构类似于自然界中的树，具有层次性。树的一个典型特点是节点之间没有环（即不存在循环路径），并且每个节点（除根节点外）有且仅有一个父节点。

树的特点：

有且仅有一个特定的根节点

当n>0时，其余节点可分为m（m>0）个不相交的有限集N1，N2....Nn,其中每个集合本身又是一棵树，叫做子树。

n=0时，为空树

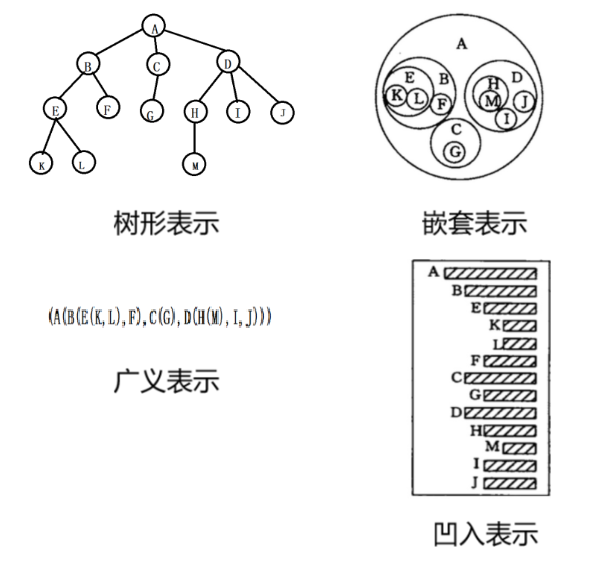
树的表示方法：

树形表示（最常见）

嵌套表示

广义表表示

凹入表示法

树的常用术语：

树的结点包含一个数据元素及若干个指向其子树的分支

**节点的度：**节点拥有的子树个数

叶子节点： 度为0的节点（终端节点）

分支节点： 度不为0的节点（非终端节点）

树的度：树内节点的度的最大值

**层次：**从根开始定义，根为第一层，根的孩子为第二层

**深度和高度：**树中节点的最大层次

**宽度：**一层中的节点个数

**有序树：**左右节点是有次序是有序树

**无序树：**左右节点是没有次序的是无序树

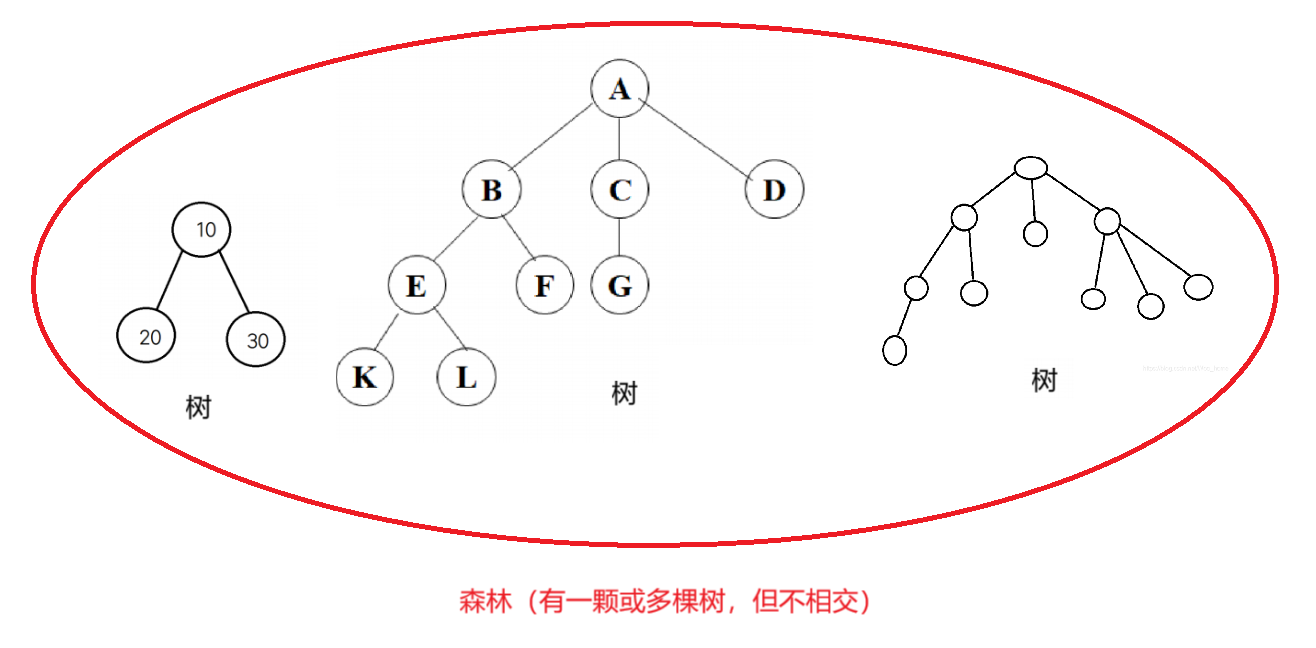
森林的概念：

森林是m棵互不相交的树的集合，对树中每一个节点而言，其子树的集合为森林。

有多颗树

但都是单独的树

树一定是森林（一棵树也可以看作森林），森林不一定为树。

树和森林的区别：树只有一个根节点，森林可以有多个根节点。

森林转换为树：

使用孩子兄弟表示法：

将孩子节点放到左节点

节点的兄弟放到右节点

将下面这棵的森林合并成树：

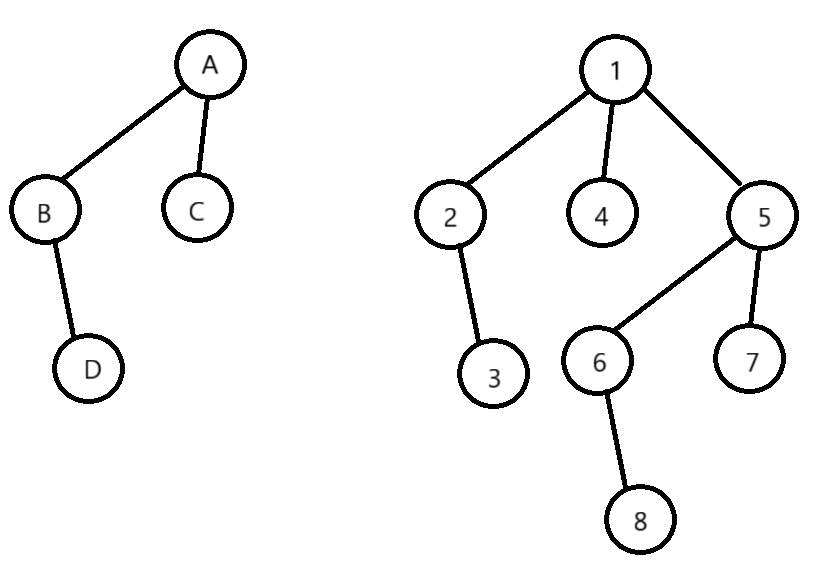
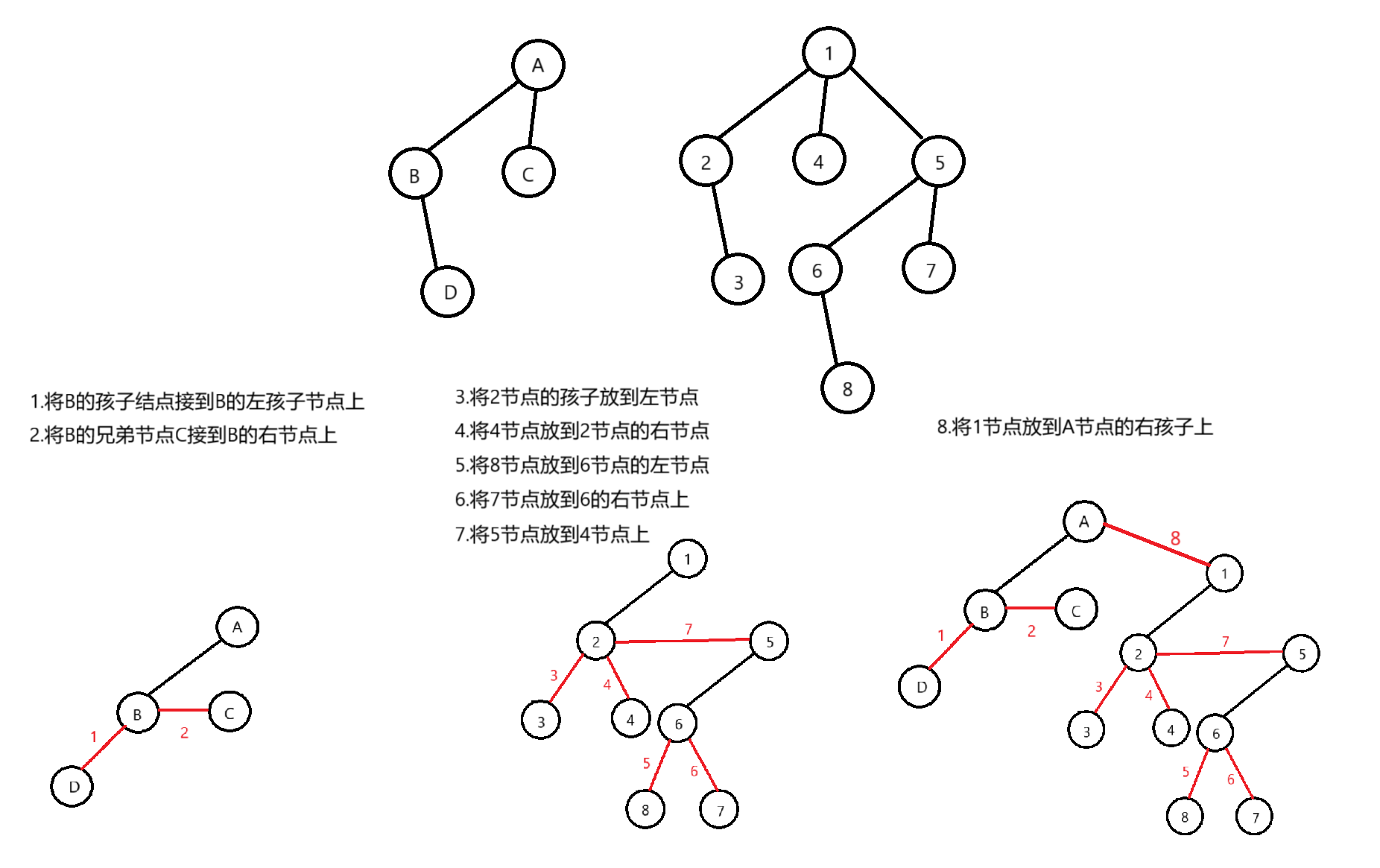
树的构建方式：

父亲表示法：

使用结构体数组：存储相应的数据和其父节点位置

优点：可以很快的找到父节点

缺点：不好找孩子节点（需要遍历数组，找父节点为x的数据）

cpp 复制代码

const int MAX_num=100;
struct Tree{
    int data;//数据
    int parent;//父亲节点间的位置
}arr[MAX_num];//创建数组

//输入数据的时候 需要输入数据和父节点的位置

孩子表示法：

使用单链表结构：存储数据及孩子节点（使用指针）

优点：可以很快找到孩子节点

缺点：不好找父节点

cpp 复制代码

const int MAX_num=100; 
struct Tree_node{
	int data;//数据
	Tree_node *child[MAX_num];//孩子指针数组 
};
Tree_node* tree;//创建一个根结点

父亲孩子表示法：

使用链式结构：存储父节点、存储数据、存储孩子节点

cpp 复制代码

const int MAX_num=100; 
struct Tree_node{
    Tree_node* parent;//保存父节点
	int data;//数据
	Tree_node *child[MAX_num];//孩子指针数组 
};
Tree_node* tree;//创建一个根结点

孩子兄弟表示法：

双链表：存储左孩子节点、数据、兄弟节点

cpp 复制代码

const int MAX_num=100; 
struct Tree_node{
	int data;//数据
	Tree_node* child;//孩子节点
    Tree_node* brother;//兄弟节点
};
Tree_node* tree;//创建一个根结点

二叉树：

二叉树特点：

二叉树的概念：

二叉树：节点至多有两颗子树（不存在度大于2的节点），二叉树的子树有左右之分，次序不能颠倒，二叉树也可以为空树。

节点基本形态：

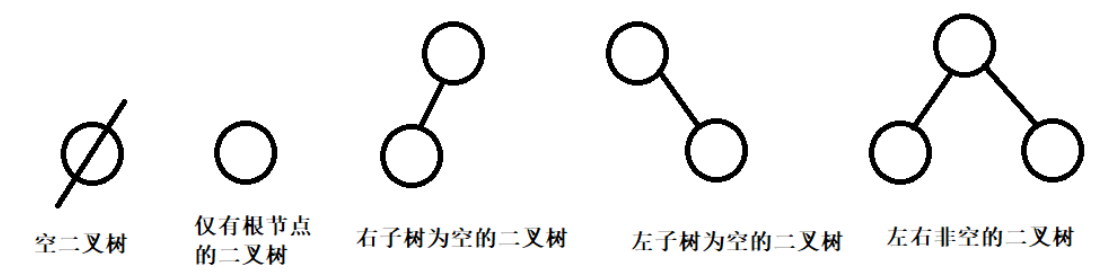
二叉树基本形态：

二叉树的性质：

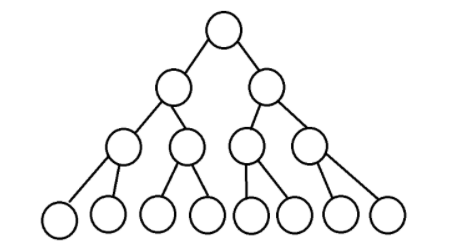
由于根节点为1：后面层数都是前面层数的2倍

二叉树的第i层最多有： 2^(i-1) 个节点（i>=1）

假设为二叉树：树的个数刚好对应的是二进制数全为1的情况

深度为K的二叉树最多有：2^K-1 个节点（K>=1）

完全二叉树的深度：由于节点数为2^k-1 所以log2后会少1，所以要加上1

具有n个节点的完全二叉树的深度为 log2(n)+1

二叉树的节点和边的关系：由于两点构成一条线，除第一条线为后面的线都会重复使用某个节点，所以边数+1=节点数

节点数=边数+1

对任意一颗二叉树T，其终端节点为N0，度为2的节点个数为N2，则N0=N2+1。

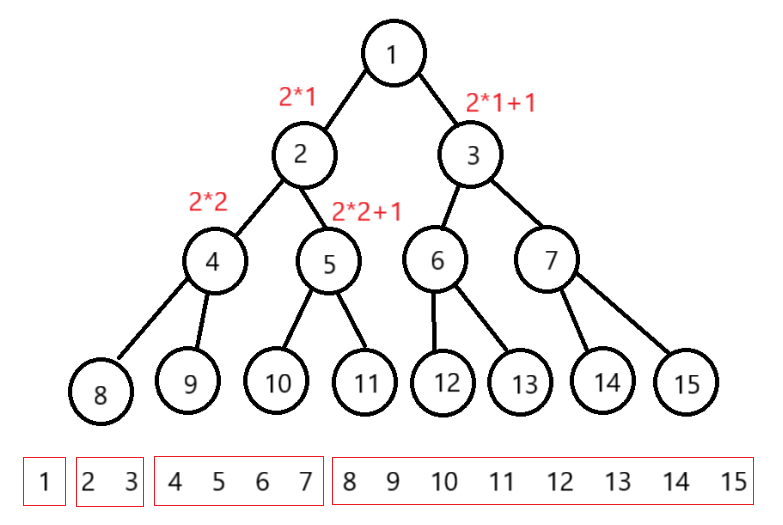
对于一个数组存储的二叉树，根节点为位置为1 ，其余节点的位置计算规律为：

N的子节点位置为：N*2（左节点）N*2+1(右节点)

N节点的父节点：N/2

特殊形态性质：

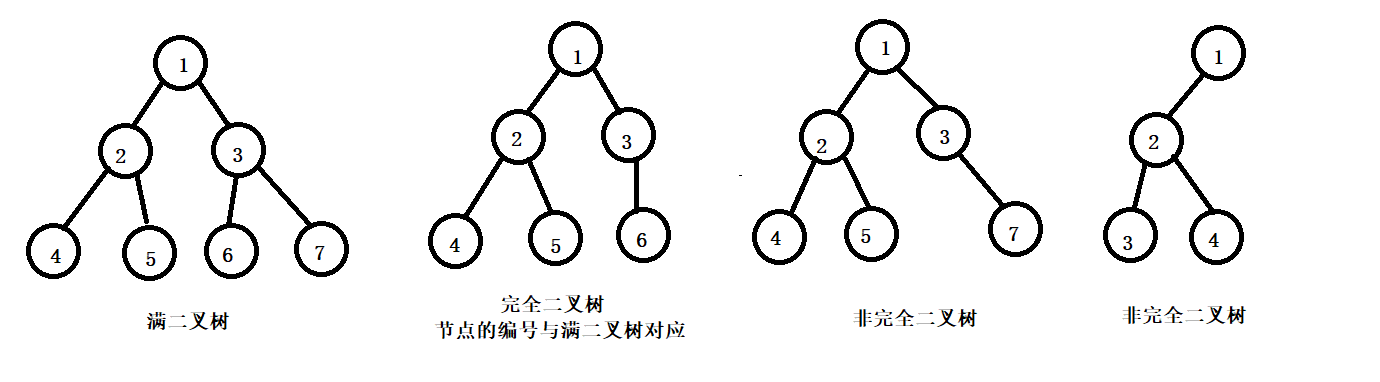
满二叉树：深度为k，且有 2^(i-1) 个节点的二叉树

完全二叉树：深度为k，有n个节点的二叉树，仅当其每一个节点都与深度为k的满二叉树中的节点位置一一对应。叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部

满二叉树是完全二叉树的特殊形态

已知节点数求二叉树的种类

使用卡特兰数：n为节点个数

二叉树存储结构：

顺序存储结构：

使用数组存储数据：按照二叉树的性质根节点的数组下标为1，其他节点N的计算：

深度为k且只有k个节点的单支树需要2^k的一维数组（下标0不使用）。

N的子节点位置为：N*2（左节点）N*2+1(右节点)

N节点的父节点：N/2

顺序结构是提前开辟了空间，这种方法适用于节点密集的情况，不然会浪费比较大的空间。

cpp 复制代码

const int Max_num=100+1;//节点个数由于0不使用，所以要多创建一个空间
int tree[Max_num];//树   根节点为下标1

淘汰赛

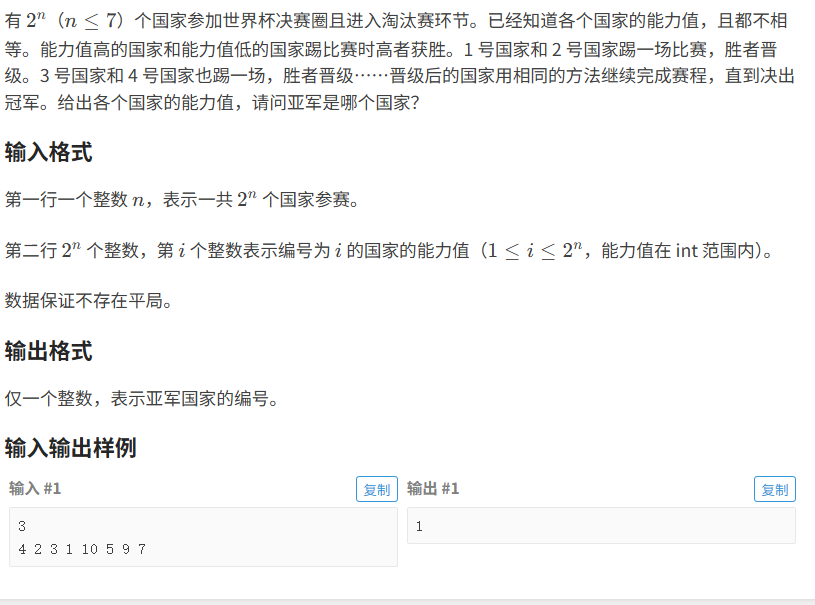
题目分析：

题目的意思是：让2^n个人进行比赛，直到比到最后，输出亚军的编号

数据是从前往后每两个1两个比较

题目的典型的树结构：刚开始在最树的最底层，慢慢往上面搭建

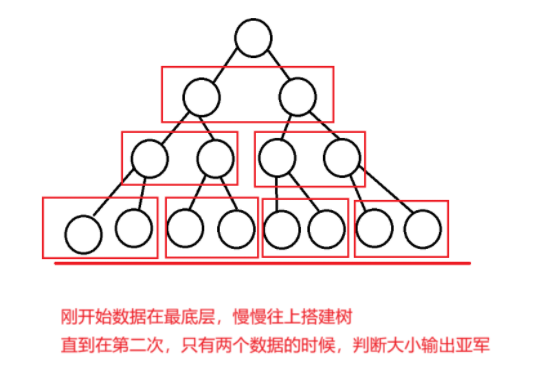
所以解题方法是逆序搭建一个树

相当于给出了最后一层的数据，往上求数据即可

编号从1开始节点为 n 的话左节点为 n*2 右节点为 n*2+1

由于最后一层的个数（2^n）是大于上面所有层数个数和的，所以创建 (2^n*2+5)数组一般会多创建几个，防止越界

最后一层的编号从 [2^n ， 2*2^n) 取不到2*2^n

从2^n-1逆推到 2即可

比较 2 和 3 的大小

然后找遍历找编号即可

相应程序：

cpp 复制代码

//使用数组模拟树结构
//节点从1开始    节点为1  子节点分别为 2 3 -> n*2 n*2+1     2节点 子节点为 4 5   3节点为 6 7
//题目给出的都是叶子节点 叶子节点树是大于 非叶子节点的 所以直接创建两倍的数组即可 
//从后往前推即可 
#include<iostream>
#include<cmath>
using namespace std;
int main(){
	int n;
	cin>>n;
	int num=pow(2,n);//获取个数
	int arr[num*2+5]={};//创建数组
	for(int i=num;i<num*2;i++)	cin>>arr[i];
	
	//从后往前推
	for(int i=num-1;i>1;i--) arr[i]=max(arr[i*2],arr[i*2+1]);
	//推完 直接对比第二和第三的大小 然后遍历数组找位置
	int data=min(arr[2],arr[3]);
    //找亚军的编号
	int index;
	for(int i=num;i<num*2;i++){
		if(arr[i]==data){
			index=i;break;
		}
	} 
	cout<<index-num+1;
	return 0;
}

链式存储结构：

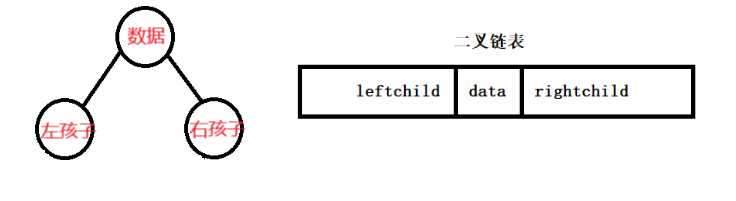
二叉链表结构：

节点数据：左孩子、数据、右孩子只用两个指针（两个分叉）

优点：节省空间，可以很快的访问到孩子节点

缺点：无法访问父节点，只能从根节点遍历树

cpp 复制代码

struct Tree_Node{
    int data;//数据
    Tree_Node *leftchild;//左孩子
    Tree_NOde *rightchild;//右孩子
};

二叉链表性质：

n个节点的二叉链表拥有n+1个空链域

n个节点的二叉链表用到的链域为n-1个（除了根节点）

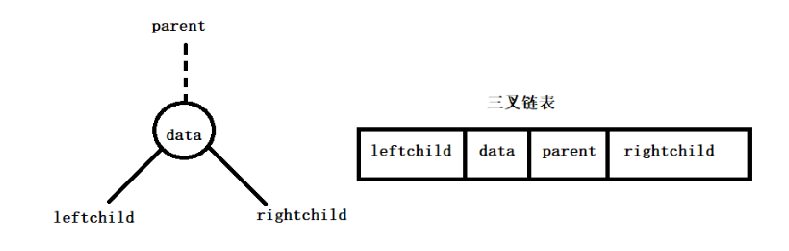
三叉链表结构：

节点数据：父节点、左孩子、数据、右节点

优点：可以找到父节点和孩子节点，可以从任何一个节点进行树的遍历

缺点：多加了一个指针，会比二叉链表消耗多一点内存

cpp 复制代码

struct Tree_Node{
    int data;//数据
    Tree_Node *parent;//父节点
    Tree_Node *leftchild;//左孩子
    Tree_NOde *rightchild;//右孩子
};

三叉链表性质：

n个节点用到的链域为：2*(n-1)

n个节点的空链域：3n- 2*(n-1) =n+2

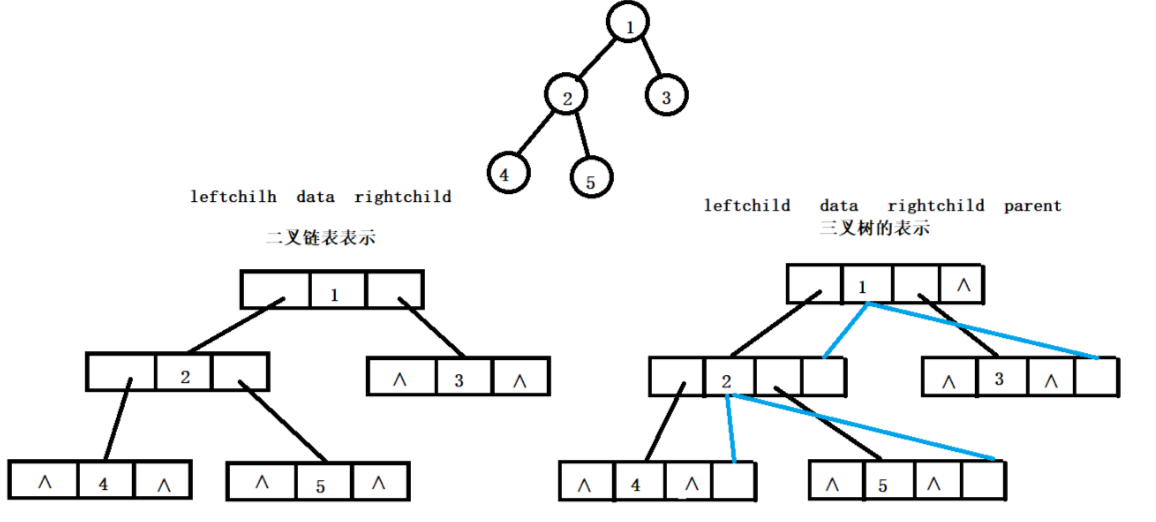
两种方法的示意图：

二叉树遍历：

二叉树的遍历：按特定的顺序去访问树中的节点，并且每个节点只访问一次，一般都是从左往右遍历。

先序遍历：

先访问根节点

再先序遍历左子树

再先序遍历右子树

cpp 复制代码

//递归的实现
void preorder(Tree_node * root){ //先序遍历
    if(root){
    	cout<<root->data<<endl;//输出节点数据
		preorder(root->leftchild);//进入左子树
		preorder(root->rightchild);//进入右子树 
    }
}

//栈的实现
//创建一个栈，根节点入栈
//获取栈顶元素，输出数据，将右节点添加到栈中
//然后将左节点添加到栈中
//当栈空的时候结束
void preorder(Tree_node * root){
	//创建一个栈
	stack<Tree_node *> sk;
	//将根节点添加到栈中
	sk.push(root); 
	//如果栈不为空，获取top元素然后添加其子节点 
	Tree_node* p=nullptr;
	while(!sk.empty()){
		p=sk.top();//获取栈顶元素
		sk.pop();//删除栈顶元素 
		if(p!=nullptr){ //不为空 
			cout<<p->data;//输出内容
			sk.push(p->rightchild);//将右孩子放到栈中
			sk.push(p->leftchild);//将左孩子放到栈中 
			//由于栈后进先出  所以会进入左子树 	
		} 	
	}
}

中序遍历：

先序遍历左子树

再访问根节点

再先序遍历右子树

cpp 复制代码

//递归的实现
void inorder(Tree_node * root){ //中序遍历 
    if(root){
		preorder(root->leftchild);//进入左子树
        cout<<root->data<<endl;//输出节点数据
		preorder(root->rightchild);//进入右子树 
    }
}

//栈的实现
//初始化一个空栈，并将当前节点设置为根节点。
//将当前节点及其所有左子节点依次压入栈中，直到左子节点为空。
//弹出栈顶节点并访问其值（即输出或处理）。
//将当前节点指向弹出节点的右子节点，重复上述过程直到栈为空且当前节点为null。
void inorder(Tree_node * root){
	//创建一个栈
	stack<Tree_node *> sk;
    Tree_node* p=root;
    while(p||!sk.empty()){
        if(p){ //一直进入左节点直到为空 
        	sk.push(p);
			p=p->leftchild;//进入左节点 
        }
        else{ //如果为空 
        	p=sk.top();//获取栈顶元素
			sk.top();//删除栈顶元素
			cout<<p->data<<endl;//输出元素
			p=p->rightchild;//进入右节点 
		} 
    }
}

后续遍历：

先序遍历左子树

再先序遍历右子树

再访问根节点

cpp 复制代码

//递归的实现
void postorder(Tree_node * root){ //后序遍历 
    if(root){
		preorder(root->leftchild);//进入左子树
		preorder(root->rightchild);//进入右子树 
        cout<<root->data<<endl;//输出节点数据
    }
}

//栈的实现
//使用双栈 一个栈存储访问的节点 一个栈记录访问的顺序
void post(Tree_node * root){
    if(root==nullptr)return ;
	//创建一个栈
	stack<Tree_node *> sk1,sk2;
    sk1.push(root);//压入根结点
    while(!sk1.empty()){
        Tree_node* node=sk1.top();
        sk1.pop();
        sk2.push(node);//压入访问的栈中
		if(node->leftchild)  sk1.push(node->leftchild);
		if(node->rightchild) sk1.push(node->rightchild);
    }
    while(!sk2.empty()){ //输出结果 
    	cout<<sk2.top()->data<<endl;
		sk2.top(); 
	}
        
}

层序遍历：

数据按照树的层数的顺序进行输出，每层的数据从左到右输出

使用队列进行实现

从根节点开始放入队列中

当队列不为空时，获取队头数据并输出，将队头的左孩子和右孩子放到栈中

删除头节点

cpp 复制代码

void Tree_Level_order(Tree_node* root){ //层序遍历
	if(root==nullptr) return;
	queue<Tree_node*> que;//创捷一个队列
	que.push(root);//将根节点放入到队列中
	while(!que.empty()){
		Tree_node* p=que.front();//获取对头数据
		if(p->leftchild) que.push(p->leftchild);//将左孩子添加到队列中
		if(p->rightchild)que.push(p->rightchild);//将右孩子添加到队列中
		cout<<p->data;//输出数据
		que.pop();//删除队头元素 
	} 
}

遍历的结果图：

二叉树基本操作：

先序创建二叉树：

给出一个先序遍历数据构建二叉树

cpp 复制代码

void pre_crt(Tree_node* root){ //输入一个节点 
	char ch;
	ch=getchar();//按照先序排序的次序输入节点
	if(ch!='!'){ //!代表结束 
		root=new Tree_node;//建立根节点
		root->data=ch;
		pre_crt(boot->leftchild);//建立左子树
		pre_crt(boot->rightchild);//建立右子树 
	} 
	else bt==nullptr;//没有数据置为空 
}

删除二叉树：

按照后序遍历删除整个二叉树

cpp 复制代码

void delete_tree(Tree_node* root){
	if(root){
		if(root->leftchild) delete_tree(root->leftchild);
		if(root->rightchild)delete_tree(root->rightchild);
		delete root;//释放内存 
	}
}

二叉树查找：

普通的二叉树查找直接使用遍历即可（先序、中序、后序）

cpp 复制代码

Tree_node* node=nullptr;//保存结果 
void Tree_find(Tree_node* root,int num){//开始查找 
	if(root&&node==nullptr){
		if(root->data==num){
			node=root;
			return;
		}
		else{
			if(root->leftchild) Tree_find(root->leftchild,num);//进入左子树 
			if(root->rightchild) Tree_find(root->leftchild,num);//进入右子树 
		}
	}
}

二叉树的深度：

遍历（先序，中序，后序）整个树

让根节点的深度为1

每次往下查找深度都要加1

最后输出 max(左子树深度，右子树深度)

cpp 复制代码

int Tree_depth(Tree_node* root){
	if(root==nullptr) return 0;
	else return max(Tree_depth(root->leftchild),Tree_depth(root->rightchild))+1;//层数需要加1 
}

题目给出一个二叉树，数组里下标1开始，1是根结点

然后分别给出该位置所对应的左孩子和右孩子的数组下标，求二叉树的深度？

cpp 复制代码

#include<iostream>
#include<algorithm>
using namespace std;
const int MAXN=2e5+5;
struct Node{
	int left,right;
}arr[MAXN];
 
int dfs(int x){
	if(!x) return 0;
	return max(dfs(arr[x].left),dfs(arr[x].right))+1;//直接返回最大的深度+1
}
int main()
{	
	cin>>n; 
	for(int i=1;i<=n;i++){
		cin>>arr[i].left>>arr[i].right;
	}
	cout<<dfs(1);
    return 0;
}

二叉树的宽度：

求宽度我们需要求数据最多的一层，所以需要保存一层的数据，可以使用层序遍历进行处理

首先需要统计当前层数的元素个数

然后分别将这些元素的左孩子和右孩子添加进来就是下一层的元素个数

创建变量保留统计最多的元素个数即可

cpp 复制代码

int Tree_width(Tree_node* root){//树的宽度
	int max_number=0;//保存最大的宽度
	if(root==nullptr) return max_number;//为空直接返回0 
	queue<Tree_node*>que;//创建一个队列
	que.push(root);
    Tree_node* p=nullptr;
	while(!que.empty()){//队列不为空
		int num=que.size();//获取当前层数的元素个数
		max_number=max(max_number,num);//更新宽度 
		while(num--){ //将这层的左孩子和有孩子添加到队列中形成下一层的全部元素 
			p=que.front();
			if(p->leftchild) que.push(p->leftchild);//将左孩子添加到队列中
			if(p->rightchild)que.push(p->rightchild);//将右孩子添加到队列中
			que.pop();//删除队头元素 
		} 
	} 
	return max_number;//返回最大宽度 
}

二叉树两节点的距离：

假设一条边为的距离为1

最后输出两个点的距离

我们可以把这个问题转换成遍历查找数据的问题

将一个节点设置为根节点，另一个节点为需要查找的节点

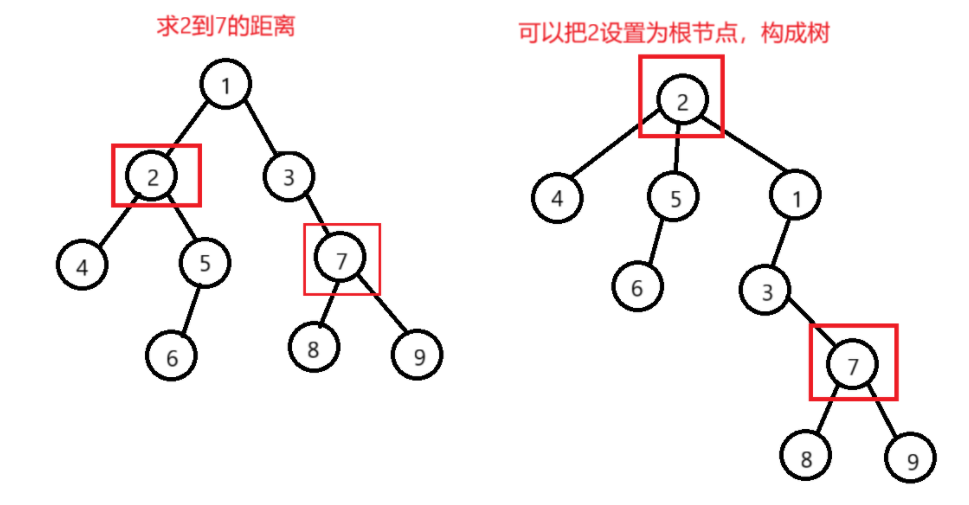
从图中可以看出，我们的节点需要保存一下父节点，这样才能完整的遍历完整个树

所以节点使用三叉链表的结构

遍历的顺序为（先序，中序，后序）三种选一种

需要特殊处理的是当遍历父节点时会出现父节点已经访问过的情况

所以对于节点我们还需要保存状态，访问过的节点就不重复访问了

每往下走距离就+1

cpp 复制代码

//方法1
int ans=0;//距离 
void Tree_Node_Distance(Tree_node* beg,Tree_node* end){
	//把起点当作根节点，开始遍历
	if(!beg||beg->b||beg==end)return ;//如果为空或已访问或找到了 就直接退出
	ans++;//距离+1 进入了下一层
	beg->b=true;//打上已访问的标记
	if(beg->leftchild)  Tree_Node_Distance(beg->leftchild,end);//搜索左子树
	if(beg->rightchild)  Tree_Node_Distance(beg->rightchild,end);//搜索右子树 
	if(beg->parent)  Tree_Node_Distance(beg->parent,end);//搜索父子树  
	ans--;//往上返回时 层数-1 
}

遍历推倒：

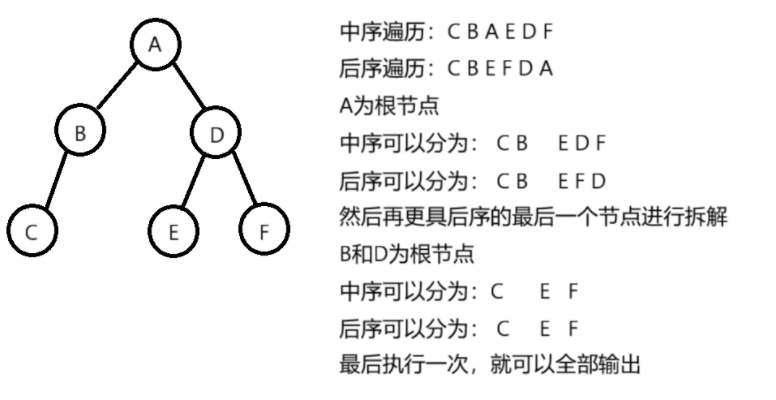
中序后序求先序：

从后序遍历序列中取出最后一个元素作为根节点。

在中序遍历序列中找到根节点的位置，左侧为左子树的中序遍历，右侧为右子树的中序遍历。

根据左子树的中序遍历长度，确定后序遍历中左子树和右子树的边界。

递归构造左子树和右子树。

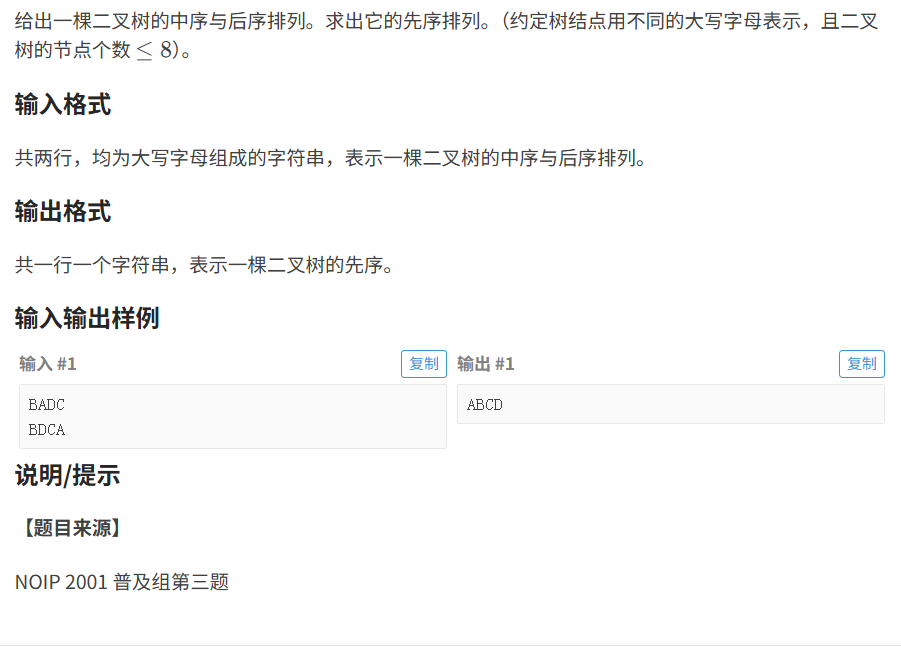
题目分析：

给出中序遍历和后序遍历求先序遍历

先序遍历：根左右

中序遍历：左根右

后序遍历：左右根

已知后序遍历：后续遍历的最后一个节点为根节点，根据A的位置对字符串进行拆解

递归拆解即可

相应程序：

cpp 复制代码

#include<iostream>
#include<string>
using namespace std;
string s1;//中序 
string s2;//后序 
void deep(string str1,string str2){
	if(str2.size()==0) return; //为空的话直接退出 
	//先输出根节点
	cout<<str2[str2.size()-1];
	//找根节点在中序遍历的位置
	int index=str1.find(str2[str2.size()-1]);
	//进入左节点
	deep(str1.substr(0,index),str2.substr(0,index));
	//进入右节点
	deep(str1.substr(index+1),str2.substr(index,str2.size()-(index+1)));
} 
int main(){
	cin>>s1>>s2;
	deep(s1,s2);
	return 0;
}

先序中序求后序：

从前序遍历序列中取出第一个元素作为根节点。

在中序遍历序列中找到根节点的位置，左侧为左子树的中序遍历，右侧为右子树的中序遍历。

根据左子树的中序遍历长度，确定前序遍历中左子树和右子树的边界。

递归构造左子树和右子树

题目分析：

给出一个数的前序遍历和中序遍历求树的后序遍历（代码的实现）

首先先序遍历的第一个为根节点

中序遍历：除根节点外可以分为左子树和右子树

先序遍历：除根节点外也可以分为左子树和右子树

递归，直到为空

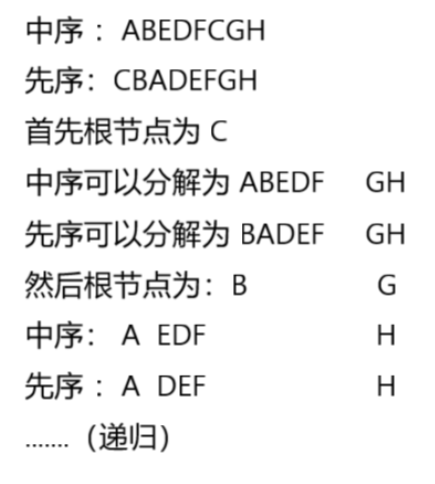
相应程序：

cpp 复制代码

#include<iostream>
using namespace std;
string s1;//中序遍历 
string s2;//先序遍历 
void deep(string n1,string n2){
	if(n2.size()==0) return;//当前序大小为空时结束，因为每次会减少一个s2的个数 
	int pos=n1.find(n2[0]);//找到根位置节点
	deep(n1.substr(0,pos),n2.substr(1,pos));//递归左子树 
	deep(n1.substr(pos+1),n2.substr(pos+1));//递归右子树
	cout<<n2[0];//输出根节点
	return; 
} 
int main(){
	cin>>s1>>s2;
	deep(s1,s2);
	return 0;
}

先序和后序求中序情况：

当二叉树的一个节点只有一个子节点时（无论是左子节点还是右子节点），在前序和后序遍历序列中，该子节点的位置会有所不同。这种情况会导致中序遍历序列的不唯一性。

前序遍历中，父节点后紧跟的是唯一的子节点。

后序遍历中，父节点前紧邻的是唯一的子节点。

题目分析：

在一颗树上若有一个若有一个结点是只有一个子结点的，那么这个子结点在左在右不影响先序后序的遍历顺序，那么总树数就要乘以2（乘法原理，这个子结点有两种选择，一种成为左子树，一种成为右子树）

我们可以得到一个规律，在先序遍历中某一元素A的后继元素B，如果在后序遍历中A的前驱元素是B，那么A只有一个子树，问题即得解

每个这类节点有两种中序遍历（及儿子在左，儿子在右）根据乘法原理中序遍历数为 2^节点个数种中序遍历

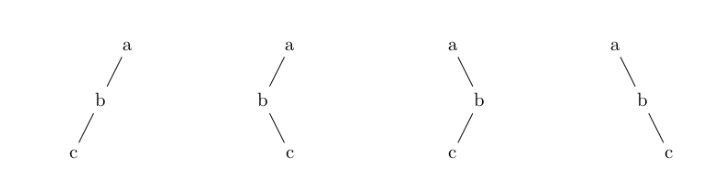
相应程序：

cpp 复制代码

#include<cstdio>
#include<algorithm>
using namespace std;
int ans;
char str1[233],str2[233];
int main()
{
        cin>>str1>>str2;//输入数据
        for(int i=0;i<strlen(str1);i++)//遍历第一个字符串
             for(int j=1;j<strlen(str2);j++) //遍历第二个字符串
              //在先序遍历中某一元素A的后继元素B，如果在后序遍历中A的前驱元素是B
              if(str1[i]==str2[j]&&str1[i+1]==str2[j-1])
                   ans++;//次数+1
        cout<<(1<<ans);//输出的是2^ans次方 
        return 0;
}