[译] 浏览器里的 Liquid Glass：利用 CSS 和 SVG 实现折射

原文日期：2025 SEP 04

前言

Apple 在 6 月的 WWDC 2025 推出了 Liquid Glass 效果------一种惊艳的让界面元素看起来像是弯曲、折射的玻璃的 UI 效果。本文是一篇关于如何通过 CSS、SVG 位移贴图和基于物理的折射计算来重建 Liquid Glass 相似效果的实践探索。

我们不追求像素级还原，而是尽可能接近 Liquid Glass，重现核心的折射和镜面高光效果，作为可以扩展的集中式概念验证（POC）。

我们会从第一性原理构建这个效果，下面先从光透过不同材质后如何弯曲开始。

范例仅支持 Chrome

文末的交互式范例只能在 Chrome 里工作（由于需要将 SVG 滤镜设置为 backdrop-filter）。你仍然可以在其它浏览器中阅读文章并与内联的模拟器交互。

理解折射

折射指的是光透过不同材质（如从空气到玻璃）时发生方向改变的现象。这种弯曲的发生是因为光的传播在不同的材质里的速度不同。

入射光和折射光角度的关系遵循斯涅尔定律：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> n 1 s i n ( θ 1 ) = n 2 s i n ( θ 2 ) n_1sin(θ_1)=n_2sin(θ_2) </math>n1sin(θ1)=n2sin(θ2)

<math xmlns="http://www.w3.org/1998/Math/MathML"> n 1 n_1 </math>n1	<math xmlns="http://www.w3.org/1998/Math/MathML"> θ 1 θ_1 </math>θ1	<math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 n_2 </math>n2	<math xmlns="http://www.w3.org/1998/Math/MathML"> θ 2 θ_2 </math>θ2
第一介质折射率	入射角	第二介质折射率	折射角

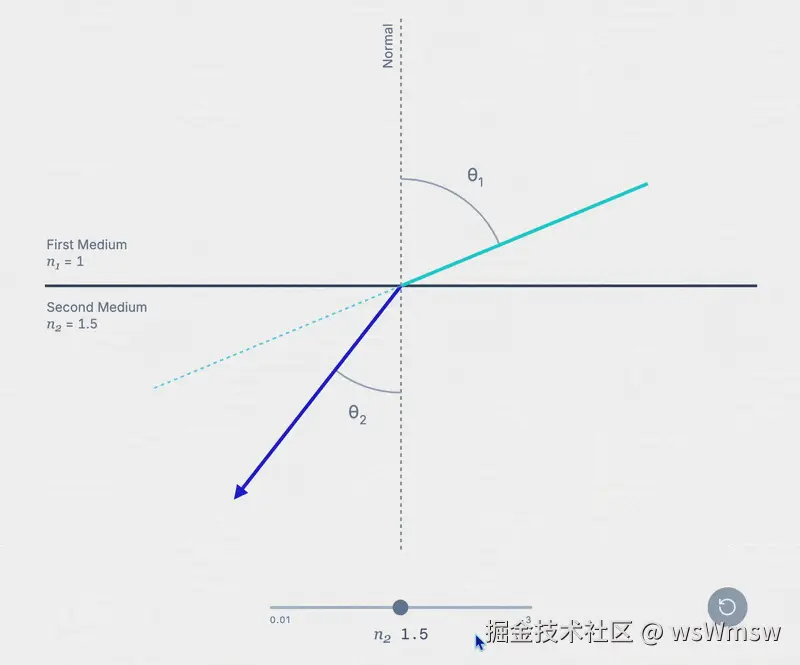
上方的交互图里，你可以看到：

当 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 = n 1 n_2=n_1 </math>n2=n1，光线直线传播，不会弯曲；
当 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 > n 1 n_2>n_1 </math>n2>n1，光线朝法线（垂直于表面的虚线）方向弯曲；
当 <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 < n 1 n_2<n_1 </math>n2<n1，光线偏离法线弯曲，改变入射角，光线也许会反射回原始介质，而不是穿过，这叫做全反射；
当入射光线和表面正交时，无论折射率如何都会直接穿过。

本项目的限制

为了不受干扰，我们通过限制场景来避免复杂的情况：

环境介质的 <math xmlns="http://www.w3.org/1998/Math/MathML"> i n d e x = 1 index=1 </math>index=1（空气）；
使用 <math xmlns="http://www.w3.org/1998/Math/MathML"> i n d e x > 1 index>1 </math>index>1 的材质，优先 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1.5 1.5 </math>1.5（玻璃）；
只发生一次折射事件（忽略后续的退出/二次折射）；
入射光线始终和背景底面垂直（无透视）；
物体都是和背景底面平行的 2D 图形（无透视）；
物体和背景底面之间无空隙（只有一次折射）；
本文仅讨论圆形，扩展为其它形状需要前期计算，圆形可以让我们只通过拉伸中间部分来构建圆角矩形。

基于这些假设，根据斯涅尔定律，我们操纵的每条光线都有明确的折射方向，并且简化了许多计算。

制作玻璃表面

为了制作玻璃效果，我们要定义这个虚拟玻璃表面的形状。想象一下镜片或曲面玻璃的剖面。

表面函数

我们用一个数学函数来描述玻璃面，函数定义了从玻璃表面任意点到曲面末端的厚度。这个表面函数 传入一个 <math xmlns="http://www.w3.org/1998/Math/MathML"> 0 0 </math>0（外边缘）到 <math xmlns="http://www.w3.org/1998/Math/MathML"> 1 1 </math>1（曲面末端，接下来是平面）之间的值，并返回所在点的玻璃高度。

ini 复制代码

const height = f(distanceFromSide);

通过高度，我们可以计算入射角，即入射光线和表面上这一点法线之间的夹角。法线就是某一点高度函数的导数，再旋转 <math xmlns="http://www.w3.org/1998/Math/MathML"> − 90 -90 </math>−90 度：

ini 复制代码

const delta = 0.001; // 接近导数的小值
const y1 = f(distanceFromSide - delta);
const y2 = f(distanceFromSide + delta);
const derivative = (y2 - y1) / (2 * delta);
const normal = { x: -derivative, y: 1 }; // 导数，再旋转 -90 度

方程

本文会用 4 种高度函数来描述不同表面形状上的折射效果：

凸面圆： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 − ( 1 − x ) 2 y=\sqrt{1-(1-x)^2} </math>y=1−(1−x)2

简单圆弧 -> 球形圆顶。比方圆形更简答，但是过渡到平面内部会更生硬，导致更锐利的折射边缘------完美圆形被拉伸之后会更明显。

凸面方圆： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 − ( 1 − x ) 4 4 y=\sqrt[4]{1-(1-x)^4} </math>y=41−(1−x)4

使用了 Apple 偏爱的方圆形：更柔和的平面 -> 即使被延展成矩形也能保持平滑的折射效果------没有生硬的内部边缘。它也能让边缘末端看起来比实际上更薄，因为最外部的平坦区域折射的光更少。

凹面： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = 1 − C o n v e x ( x ) y=1-Convex(x) </math>y=1−Convex(x)

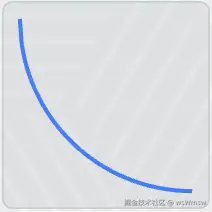
凹面形状是凸面圆的补形，形成了一个碗状下凹。这种形状使光线向外分叉，超出玻璃边界。

唇形： <math xmlns="http://www.w3.org/1998/Math/MathML"> y = m i x ( C o n v e x ( x ) , C o n c a v e ( x ) , S m o o t h e r s t e p ( x ) ) y=mix(Convex(x), Concave(x), Smootherstep(x)) </math>y=mix(Convex(x),Concave(x),Smootherstep(x))

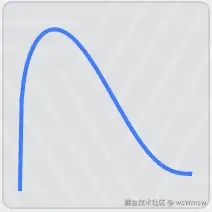
通过 Smootherstep 混合凹面和凸面：边缘抬起，中央微沉。

我们可以添加更多变量使表面函数更复杂，但是这 4 个方程已经足以展示表面形状如何影响折射了。

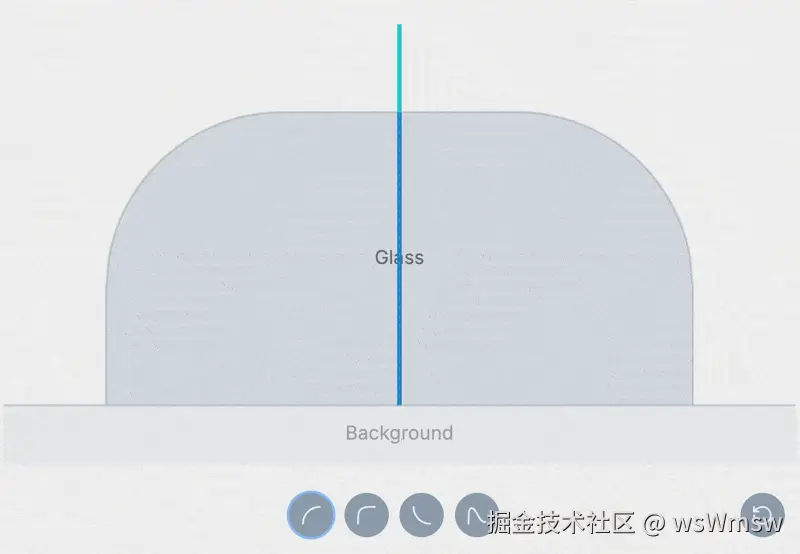
模拟

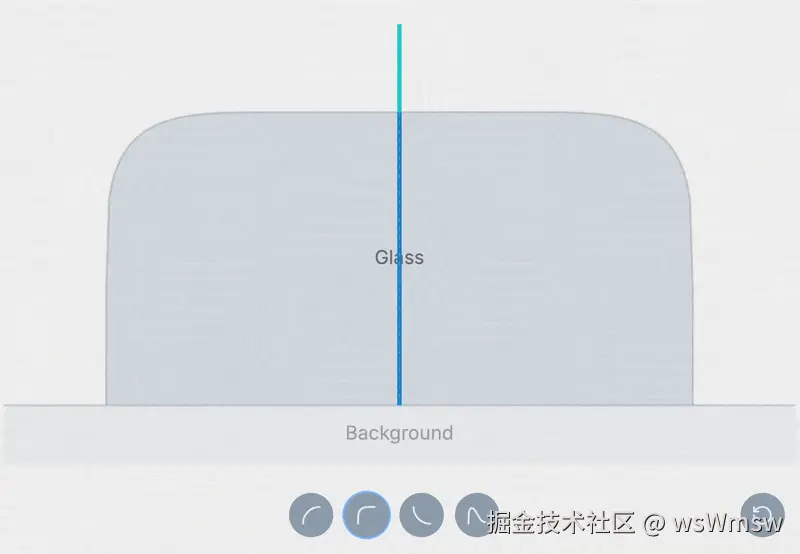
现在，让我们通过可交互的光线追踪模拟来理解表面函数的实际场景。下面的可视化展示了光线穿过不同表面的行为，帮助我们理解数学方程的实际影响。

凸面圆	凸面方圆	凹面	唇形

从模拟中可以看到，凹面会把光线推出玻璃，凸面则是射进玻璃中。

我们希望避免向外位移，因为这就要对物体外部进行采样。Apple 的 Liquid Glass 偏爱凸形轮廓（Switch 组件除外，后面介绍）。

背景底面的箭头是指位移------与没有玻璃相比，经过玻璃折射的光线落到背景的距离。颜色表示大小（越远 -> 越紫）。

关于对称性：光线距离边界有相同的距离，则任意一边都共享相同的位移大小。计算一次，处处复用。

位移矢量场

既然我们已经计算了光线距离边界的位移，现在让我们计算整个玻璃表面的位移矢量场。

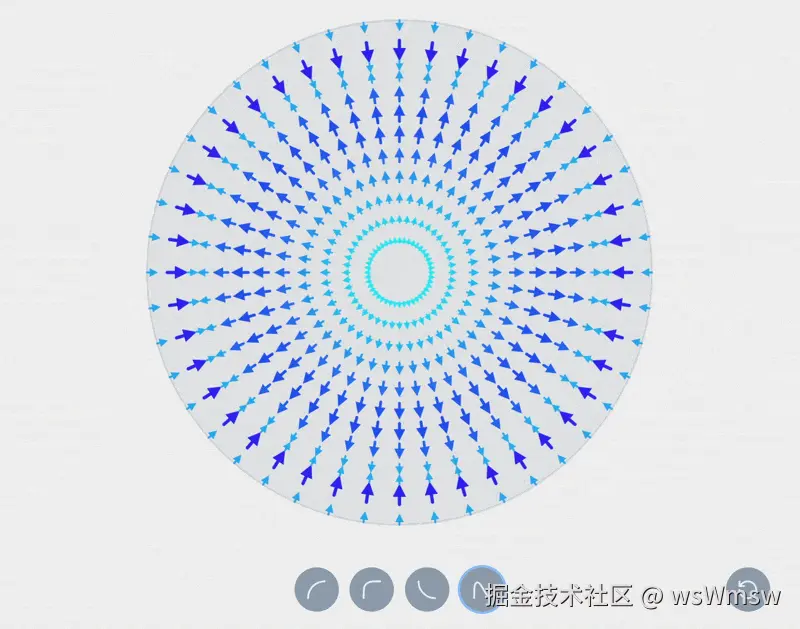
矢量场指的是玻璃上每一处有多少光线从初始位置位移，以往什么方向位移。在本文中，位移始终垂直玻璃边缘。

预计算位移大小

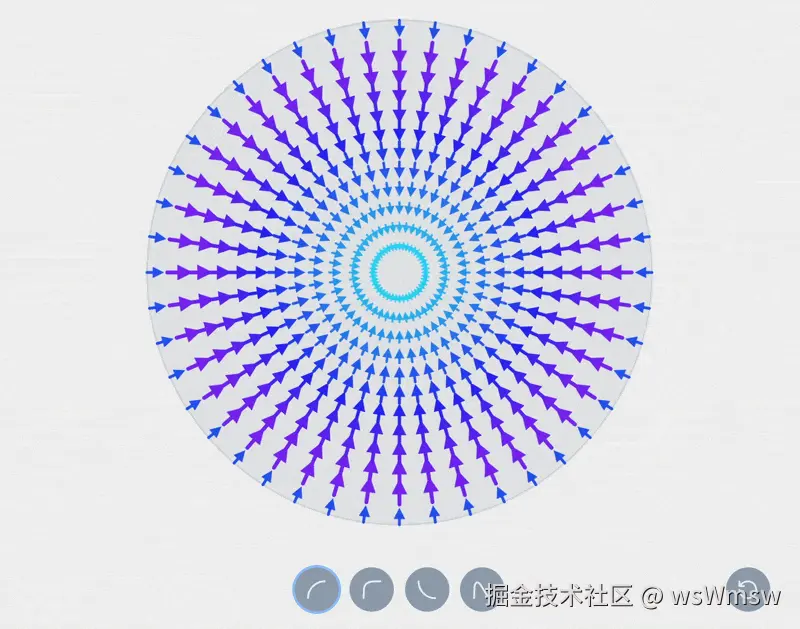
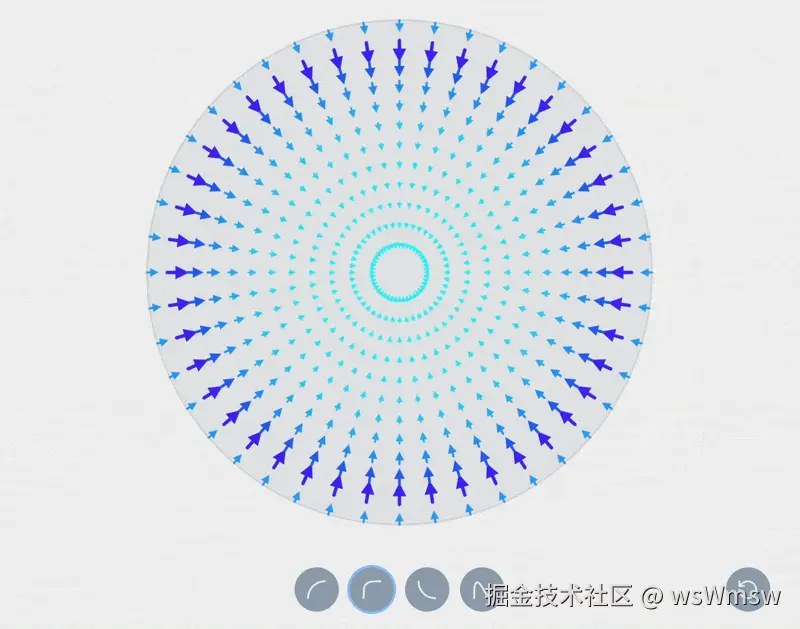
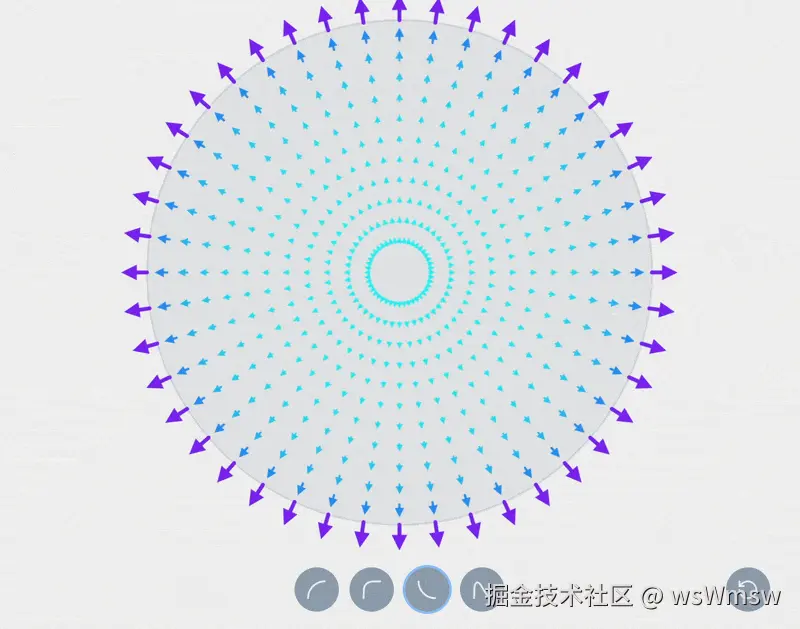
由于我们看到位移大小是围绕曲面末端对称的，我们可以预先计算一个半径上的曲面部分。

这让我们只通过二维（x 和 z 轴）、物体的"一半截面"上就能完成所有计算，然后再将计算结果绕 z 轴旋转即可。

在半径上，我们需要 127 条光线作为实际样本，这取决于 SVG 位移贴图分辨率限制（将在下一章介绍）。

凸面圆	凸面方圆	凹面	唇形

归一化向量

上图里为了可视化，箭头是等比缩小的，所以它们没有重合。这是种归一化，并且从技术角度看也是有用的。

为了在位移贴图里使用这些向量，我们需要归一化。归一化意味着缩放向量，使最大值为 1，以便我们在固定的范围内表示向量。

我们先通过预先计算的数组得到最大位移值：

javascript 复制代码

const maximumDisplacement = Math.max(...displacementMagnitudes);

然后我们将每个向量值除以最大值：

javascript 复制代码

displacementVector_normalized = {
  angle: normalAtBorder,
  magnitude: magnitude / maximumDisplacement,
};

我们要将 maximumDisplacement 存储下来，后面我们需要它将位移贴图转换回真实大小。

SVG 位移贴图

现在我们需要将数学的折射计算转为浏览器可以实际渲染的东西。我们会用到 SVG 位移贴图。

位移贴图只是一张图片，其中每个像素的颜色会告诉浏览器多远可以从当前位置找到真实像素。

SVG 的 <feDisplacementMap /> 把这些像素编码进了一个 32 比特的 RGBA 图像中，每个通道表示不同轴的位移。

用户负责定义通道对应的轴，但是理解限制也很重要：由于每个通道是 8 比特，所以位移在每个方向的限制范围是 -128 到 127。（共 256 个值）128 表示中间值，表示没有位移。

SVG 滤镜只能用图像作为位移贴图，所以我们要将位移矢量场转为图像格式。

jsx 复制代码

<svg colorInterpolationFilters="sRGB">
  <filter id={id}>
    <feImage
      href={displacementMapDataUrl}
      x={0}
      y={0}
      width={width}
      height={height}
      result="displacement_map"
    />
    <feDisplacementMap
      in="SourceGraphic"
      in2="displacement_map"
      scale={scale}
      xChannelSelector="R" // Red Channel for displacement in X axis
      yChannelSelector="G" // Green Channel for displacement in Y axis
    />
  </filter>
</svg>

上面的代码中，<feDisplacementMap /> 使用红色通道表示 X 轴，绿色通道表示 Y 轴。蓝色通道和 alpha 通道忽略不使用。

缩放

绿色（X）通道和红色（Y）通道是 8 比特值（0-255）。不考虑额外的缩放，它们会线性映射到归一化的位移 [-1, 1] 中，128 是中间值（无位移）：

rust 复制代码

  0 -> -1
128 -> 0
255 -> 1

<feDisplacementMap /> 的 scale 属性乘以归一化后的值：

rust 复制代码

  0 -> -scale
128 -> 0
255 -> scale

由于我们的向量使用最大位移值作为一个单位做归一化，所以我们可以使用这个最大值作为滤镜的 scale：

jsx 复制代码

<feDisplacementMap
  in="SourceGraphic"
  in2="displacement_map"
  scale={maximumDisplacement} // 最大位移 (px) → 真实像素偏移
  xChannelSelector="R"
  yChannelSelector="G"
/>

你也可以通过动画 animate 来淡入淡出这种效果------无需重新计算贴图（即使不完全符合物理定律，但是对艺术控制有用）。

向量的红绿值

为了将位移矢量场转为位移贴图，我们要将每个向量转为色值。红色通道将表示向量的 X 分量，而绿色通道将表示向量的 Y 分量。

我们现在拥有每个向量的极坐标（角度和大小），所以在映射到红绿通道前，我们要将它们转为笛卡尔坐标（X 和 Y）。

javascript 复制代码

const x = Math.cos(angle) * magnitude;
const y = Math.sin(angle) * magnitude;

由于我们已经归一化了向量，magnitude 在这里是 0 到 1。

现在开始，我们只要给红绿通道的值重新映射为 0 到 255 之间。

javascript 复制代码

const result = {
  r: 128 + x * 127, // Red channel is the X component, remapped to 0-255
  g: 128 + y * 127, // Green channel is the Y component, remapped to 0-255
  b: 128, // Blue channel is ignored
  a: 255, // Alpha channel is fully opaque
};

在为每个向量转为色值之后，我们就得到了一个在 SVG 滤镜中可以作为位移贴图使用的图像了。

操场

这个例子将 SVG 位移滤镜用在一个简单场景里，让你可以调整表面形状、曲面宽度、玻璃厚度和缩放大小。观察这些输入是如何改变折射、生成的位移贴图和最终的渲染。

镜面高光

高光是 Liquid Glass 效果的最后一部分------当光线从特定角度射到玻璃，就能看到那些明亮的、闪亮的边缘。

Apple 似乎是用一种简单的边缘光效果来实现的，高光围绕在玻璃物体的边缘，并且高光的强度根据表面法线相对于固定光线的方向之间的夹角决定。

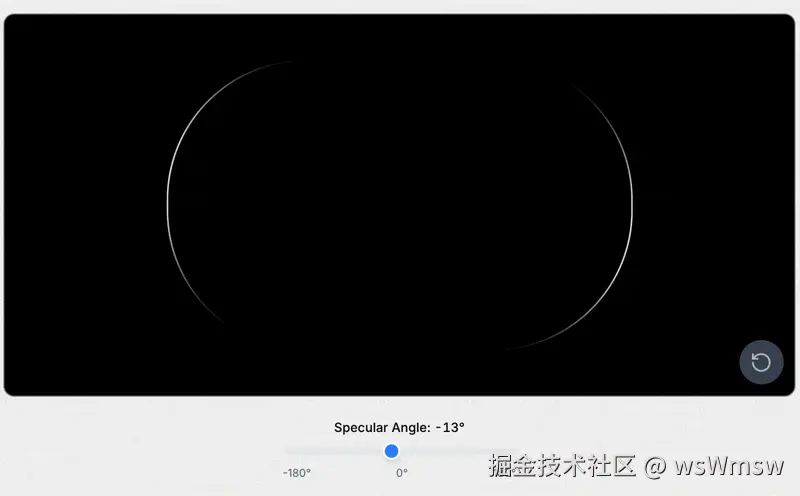
组合折射与镜面高光

最终的 SVG 滤镜，我们会组合用于折射的位移贴图和镜面高光效果。

两者都使用 <feImage /> 单独加载，然后使用 <feBlend /> 结合来让高光重叠在折射的图像之上。

而这一部分实际是整个效果里最"创意"的部分，只需要调整滤镜的数量和参数，就能获得各种不同的视觉效果。

SVG 滤镜作为 `backdrop-filter`

这一部分是跨浏览器兼容的终结。目前只有 Chrome 支持使用 SVG 滤镜作为 backdrop-filter，而这是为 UI 组件添加 Liquid Glass 效果的关键：

css 复制代码

.glass-panel {
  backdrop-filter: url(#liquidGlassFilterId);
}

注意：backdrop-filter 的尺寸不会根据元素的大小自动调整，所以你必须确保滤镜图像的尺寸要符合元素的大小。

现在我们已经准备就绪，我们可以创建使用这种效果的组件了。

串起来：真正的 UI 组件

我们的折射数学公式和位移贴图已经正常工作了，接下来让我们看看如何将它们翻译成也许会在应用中使用的真实的 UI 组件。

我们的目标不是为生产环境创建真实、完善的组件，只是为了浅尝体验一下这种效果在不同的 UI 元素上的感觉。

放大镜玻璃

这个组件实际上使用了两个位移贴图：一个用于边缘的折射，另一个用于放大，使得拥有更强的折射效果。

它还用阴影和抖动缩放构建了更动态、具交互性的效果。

搜索框

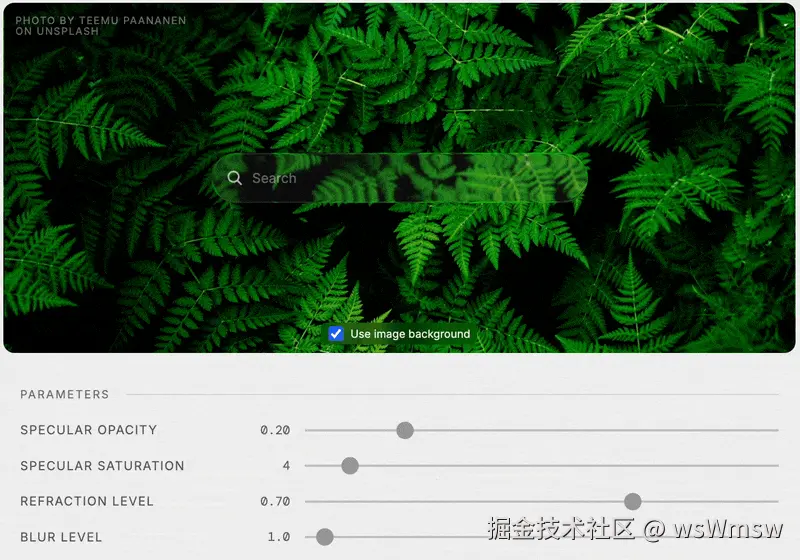
开关

这个组件使用了唇形玻璃，使得表面的外侧是凸形，中央是凹形。这让滑块中间缩小，让边缘折射内部。

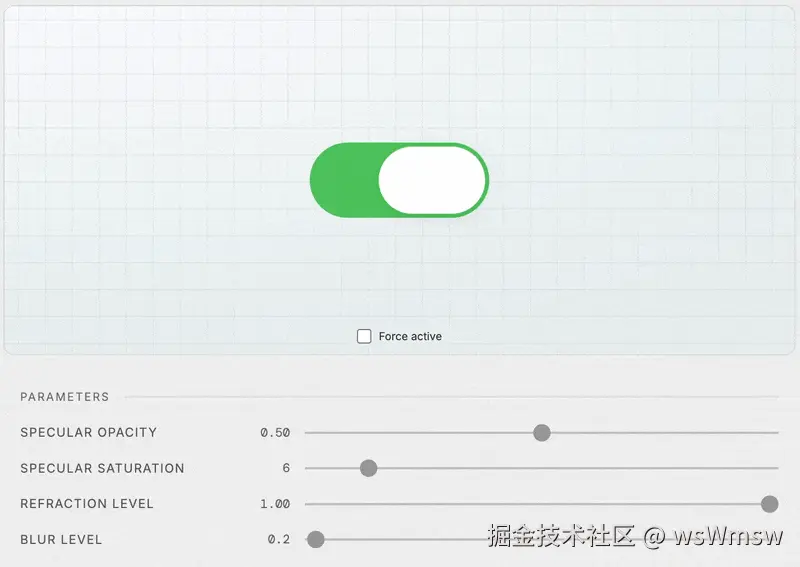
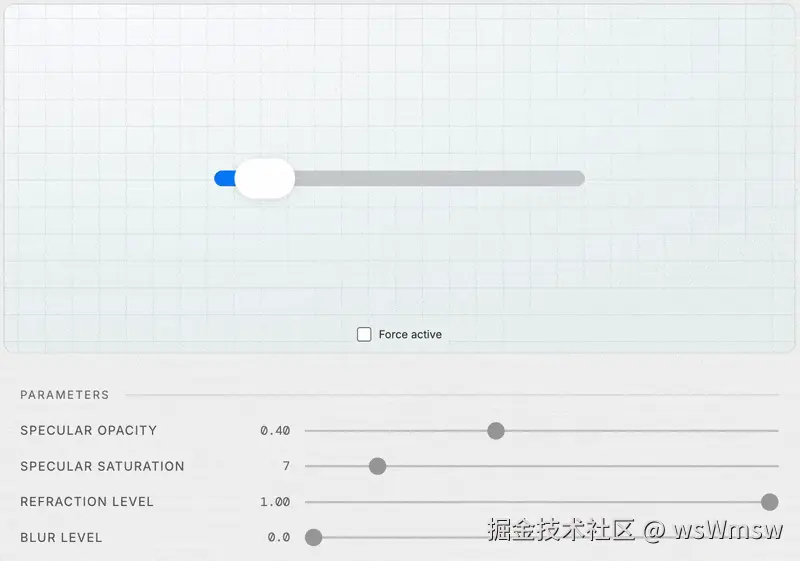
滑块

滑块让你可以透过玻璃看到当前级别，同时边缘折射背景。它使用了凸形玻璃。

音乐播放器

这个复刻版播放器 UI 试图模仿 Apple Music 的玻璃面板观感，使用了凸面玻璃和细微的镜面高光。

它依赖 iTunes 搜索接口来获取专辑封面和歌曲细节。

总结

这个原型将 Apple 的 Liquid Glass 提取为了带有边缘高光的实时折射效果。它是可扩展的，但仍是 Chrome 绑定的------只有 Chromium 让 SVG 滤镜作为 backdrop-filter。也即，它在基于 Chromium 的运行时仍然是可行的，如 Electron，其它情况你可以制作一个假的模糊背景作为回退。

请实验性地谨慎对待。由于每一次调整都会强制重建所有位移贴图，因此动态的形状/尺寸的微调（动画中的 <filter /> 属性，如 scale）现在有昂贵开销。

在开源之前，源码需要清理及性能优化。

感谢您阅读我的第一篇博文------我由衷接受任何反馈、想法、批评或建议。如果它碰撞了灵感，或是你知道有喜欢这类深入探索文章的人，请随意分享传递。

[译] 浏览器里的 Liquid Glass：利用 CSS 和 SVG 实现折射

前言

理解折射

本项目的限制

制作玻璃表面

表面函数

方程

模拟

位移矢量场

预计算位移大小

归一化向量

SVG 位移贴图

缩放

向量的红绿值

操场

镜面高光

组合折射与镜面高光

SVG 滤镜作为 backdrop-filter

串起来：真正的 UI 组件

放大镜玻璃

搜索框

开关

滑块

音乐播放器

总结

SVG 滤镜作为 `backdrop-filter`