Mean Flows for One-step Generative Modeling
Zhengyang Geng 1 Mingyang Deng 2 Xingjian Bai 2 J. Zico Kolter 1 Kaiming He2
1 CMU 2 MITWork partly done when visiting MIT.
https://arxiv.org/pdf/2505.13447
https://github.com/Gsunshine/meanflow
Abstract
We propose a principled and effective framework for one-step generative modeling. We introduce the notion of average velocity to characterize flow fields, in contrast to instantaneous velocity modeled by Flow Matching methods. A well-defined identity between average and instantaneous velocities is derived and used to guide neural network training. Our method, termed the MeanFlow model, is self-contained and requires no pre-training, distillation, or curriculum learning. MeanFlow demonstrates strong empirical performance: it achieves an FID of 3.43 with a single function evaluation (1-NFE) on ImageNet 256×256 trained from scratch, significantly outperforming previous state-of-the-art one-step diffusion/flow models. Our study substantially narrows the gap between one-step diffusion/flow models and their multi-step predecessors, and we hope it will motivate future research to revisit the foundations of these powerful models.
本文提出了一种原理清晰且高效的单步生成建模框架。与流匹配方法建模瞬时速度不同，本研究引入了平均速度 的概念来描述流场。通过推导平均速度与瞬时速度之间明确定义的恒等式，并以此指导神经网络训练。所提出的MeanFlow模型自成体系，无需预训练、蒸馏或课程学习。MeanFlow展现出强大的实证性能：在ImageNet 256×256数据集上从头训练，仅通过单次函数评估（1-NFE）即可获得3.43的FID分数，显著超越现有最先进的单步扩散/流模型。这项研究大幅缩小了单步扩散/流模型与多步模型之间的性能差距，有望推动学界重新审视这些强大模型的理论基础
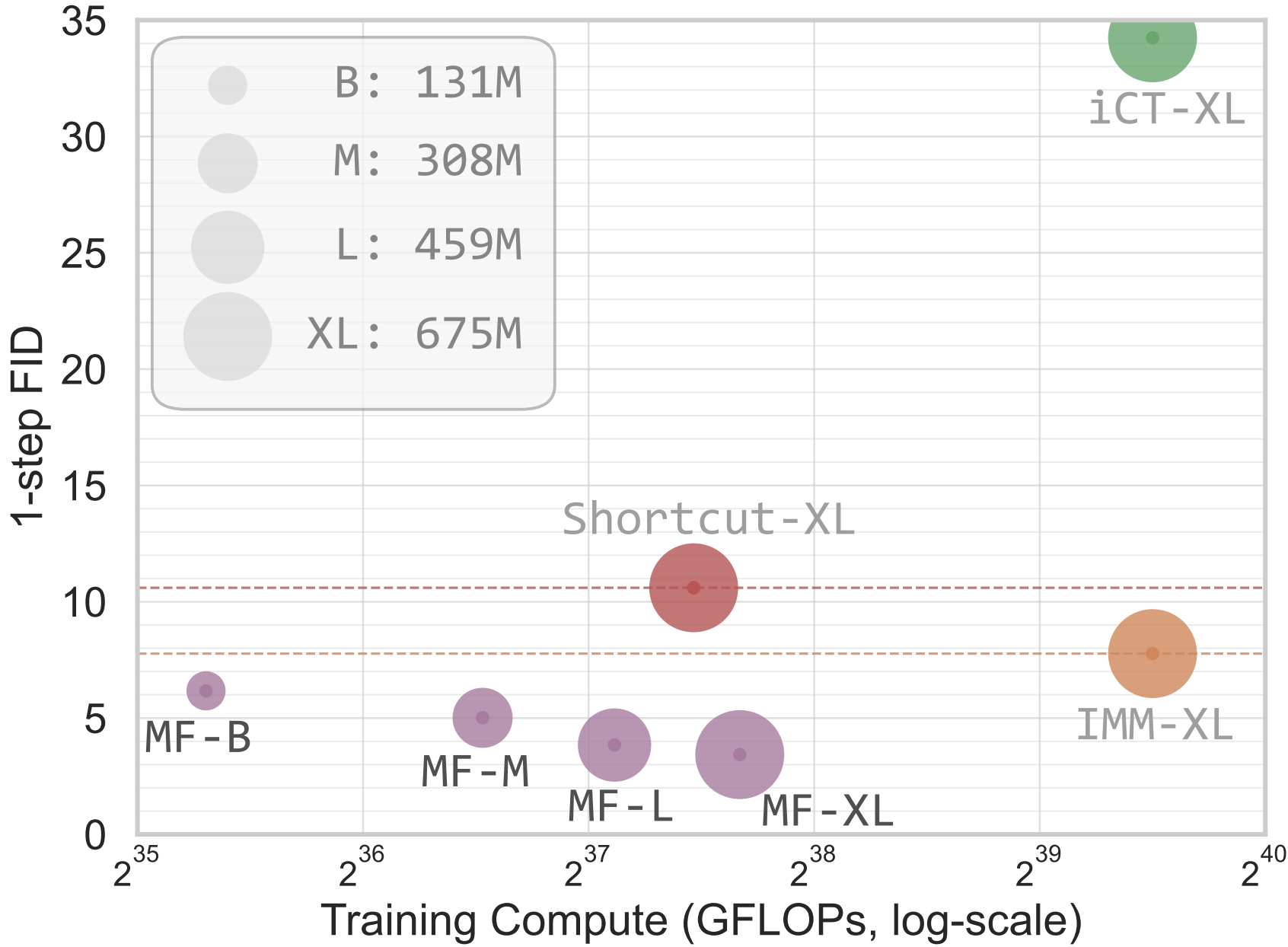
Figure 1:One-step generation on ImageNet 256×256 from scratch. Our MeanFlow (MF) model achieves significantly better generation quality than previous state-of-the-art one-step diffusion/flow methods. Here, iCT [43], Shortcut [13], and our MF are all 1-NFE generation, while IMM's 1-step result [52] involves 2-NFE guidance. Detailed numbers are in Tab. 2. Images shown are generated by our 1-NFE model.
1 Introduction
生成建模的核心目标是将先验分布转换为数据分布。流匹配技术提供了一个直观且概念简洁的框架，通过构建流路径实现分布间的转换。与扩散模型密切相关的流匹配方法，重点关注指导模型训练的速度场。自提出以来，该方法已在现代生成建模中得到广泛应用。
传统流匹配与扩散模型在生成过程中均需迭代采样。近期研究开始重点关注少步长（特别是单步前馈）生成模型。作为开创性工作，一致性模型通过沿相同路径采样的输入施加一致性约束于网络输出。虽然成果令人鼓舞，但一致性约束仅作为网络行为的特性被引入，而指导学习的真实流场本质特性仍属未知。这导致训练过程不稳定，且需要精心设计"离散化课程"来逐步约束时间域。
本研究提出名为MeanFlow 的原理化高效单步生成框架。其核心思想是引入表征平均速度 的新真实流场，区别于流匹配中通常建模的瞬时速度。平均速度定义为位移与时间间隔的比值，而位移由瞬时速度的时间积分给出。基于这一定义，推导出平均速度与瞬时速度之间明确的内在关联，自然构成了指导网络训练的原理基础。
在此基础概念上，训练神经网络直接建模平均速度场。通过引入损失函数促使网络满足平均速度与瞬时速度的内在关系，无需额外的一致性启发式规则。真实目标流场的存在确保最优解原则上独立于特定网络结构，这在实际训练中可带来更稳健的性能。进一步证明该框架可自然将无分类器引导技术融入目标场，在使用引导时不会增加采样时的额外成本。
MeanFlow模型在单步生成建模中展现出卓越的实证性能。在ImageNet 256×256数据集上，采用1-NFE生成即可获得3.43的FID分数，相对现有同类最佳方法提升50%至70%（图1）。此外，该方法作为自包含的生成模型：完全从头开始训练，无需任何预训练、蒸馏或课程学习。本研究基本消除了单步扩散/流模型与多步模型之间的性能差距，有望推动未来研究重新审视这些强大模型的奠基理论。
2 Related Work
（略）
3 Background: Flow Matching
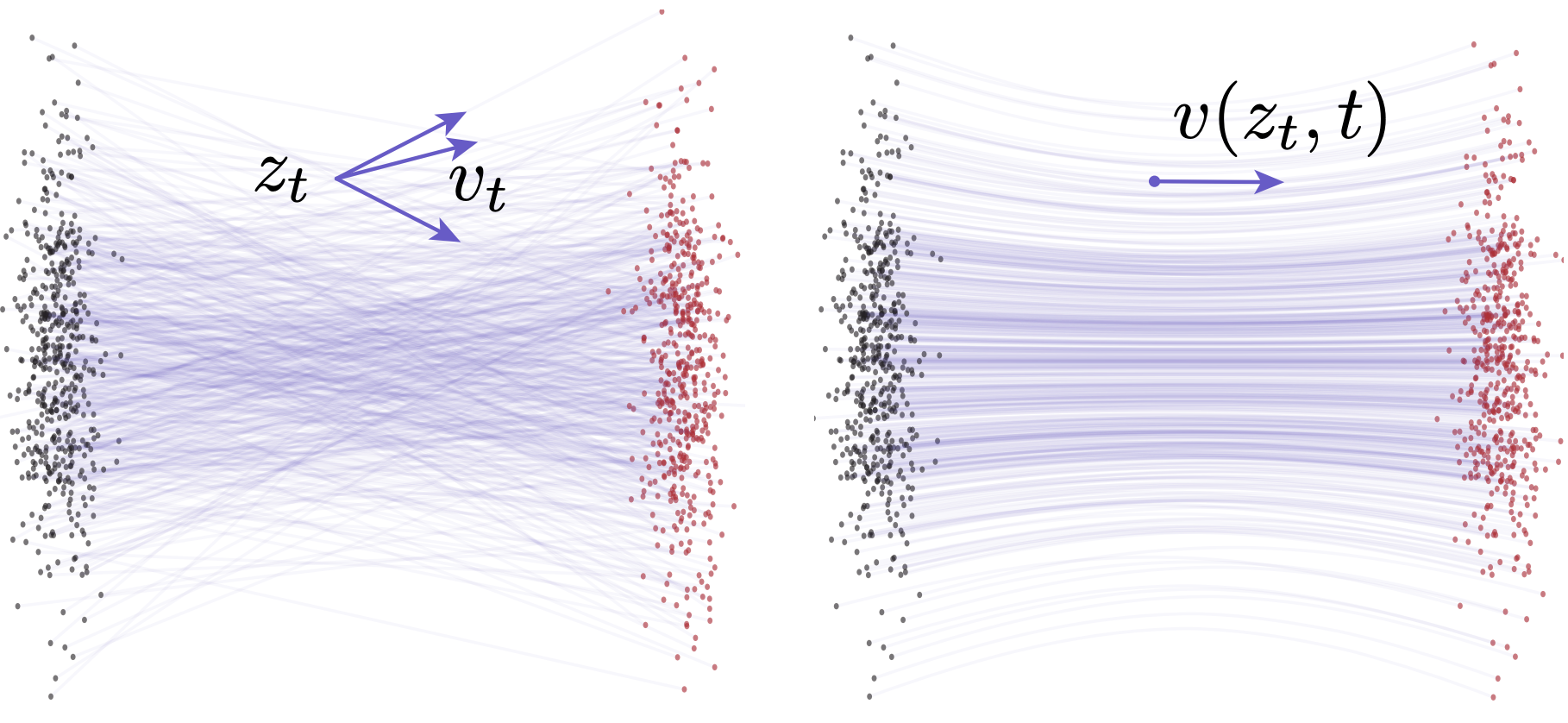
Figure 2: Velocity fields in Flow Matching [28]. Left: conditional flows [28]. A given zt can arise from different (x,ϵ) pairs, resulting in different conditional velocities vt. Right: marginal flows [28], obtained by marginalizing over all possible conditional velocities. The marginal velocity field serves as the underlying ground-truth field for network training. All velocities shown here are essentially instantaneous velocities. Illustration follows [12]. (Gray dots: samples from prior; red dots: samples from data.)
流匹配是通过学习两个概率分布间的速度场来匹配流线的生成模型族。给定数据分布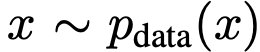
和先验分布
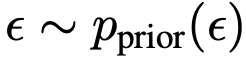，可构建流路径
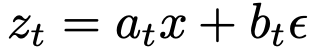，其中速度场定义为
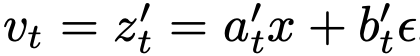（'表示时间导数）。该速度在文献中称为条件速度（图2左）。常用调度方案
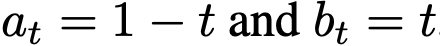会产生
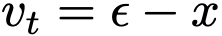的速度场。
由于给定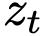
及其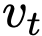
可能源于不同的x和ε组合，流匹配本质上是建模所有可能性的期望，即边际速度（图2右）：
通过神经网络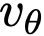
拟合该边际速度场：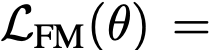
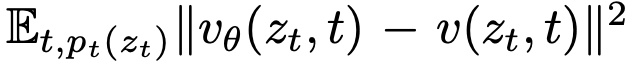。虽然该损失函数因式(1)的边际化而难以直接计算，但可采用条件流匹配损失进行替代优化：
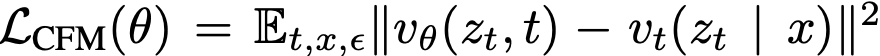。最小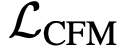化
等价于优化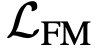
。
给定边际速度场v(z_t,t)，通过求解常微分方程
从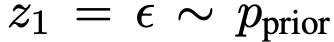
开始生成样本。数值解可表示为：
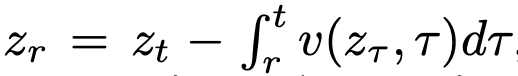。实践中该积分通过离散时间步进行数值近似，例如一阶欧拉法的迭代格式： 
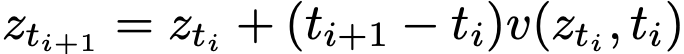。亦可采用更高阶求解器。
需注意的是，即使条件流被设计为直线路径，边际速度场（式1）通常仍会导致弯曲轨迹（图2示意）。这种非直线特性不仅是神经网络近似的结果，更源于底层真实边际速度场的本质属性。当在弯曲轨迹上采用粗粒度离散化时，数值ODE求解器会导致显著误差。
4 MeanFlow Models
4.1 Mean Flows
本方法的核心思想是引入表征平均速度 的新流场，而流匹配方法建模的是瞬时速度。
Average Velocity.
平均速度定义为两个时间步 t 与 r 之间的位移（通过积分获得）与时间间隔的比值。形式化表示为：
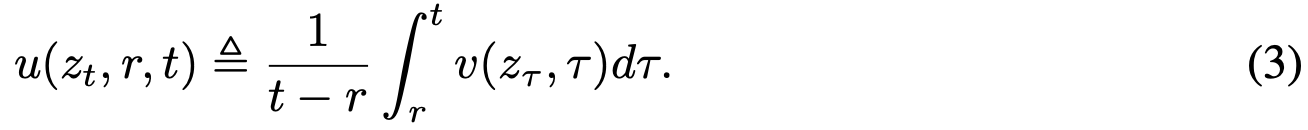
为强调概念差异，全文使用符号 u 表示平均速度，v 表示瞬时速度。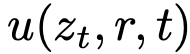
是一个同时依赖于 (r, t) 的流场。u 场如图 3 所示。需注意，平均速度 u 本质上是瞬时速度 v 的泛函：即 
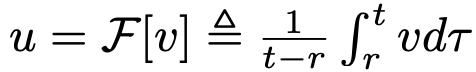。它是由 v 诱导产生的场，不依赖于任何神经网络。概念上，正如瞬时速度 v 作为流匹配中的真实流场，平均速度 u 在本框架中为学习提供了底层真实流场。
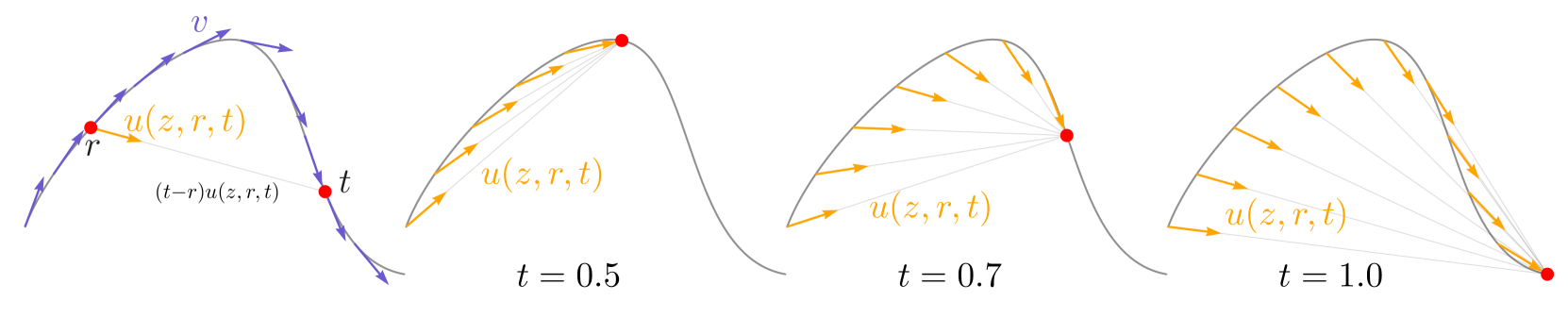
Figure 3:The field of average velocity u(z,r,t). Leftmost: While the instantaneous velocity v determines the tangent direction of the path, the average velocity u(z,r,t), defined in Eq. 3, is generally not aligned with v. The average velocity is aligned with the displacement, which is (t−r)u(z,r,t). Right three subplots: The field u(z,r,t) is conditioned on both r and t, and is shown here for t=0.5, 0.7, and 1.0.
根据定义，u 场满足特定边界条件与"一致性"约束。当 r→t 时，满足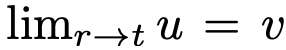 
。此外，自然满足一种"一致性"：对任意中间时间 s，在 [r, t] 上执行单大步长与在 [r, s] 和 [s, t] 上执行两个连续小步长具有一致性。观察到，
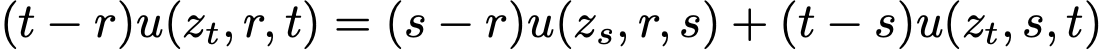这直接源于积分的可加性：
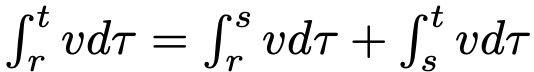。因此，准确逼近真实 u 的网络预期将自然满足一致性关系，无需显式约束。
MeanFlow 模型的最终目标是通过神经网络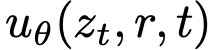 
近似平均速度。该方法具有显著优势：若能准确近似该量，则可通过单次评估 
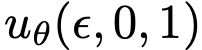来近似整个流路径。这意味着该方法更适用于单步或少步生成，因为在推理时无需显式近似时间积分------这是建模瞬时速度时的必要步骤。然而，直接使用式(3)定义的平均速度作为网络训练的真实目标不可行，因其需在训练期间计算积分。关键洞见在于，平均速度的定义式可通过变换构建出适用于训练的优化目标，即使仅能获取瞬时速度。
The MeanFlow Identity.
为使公式适用于训练，将式(3)改写为：
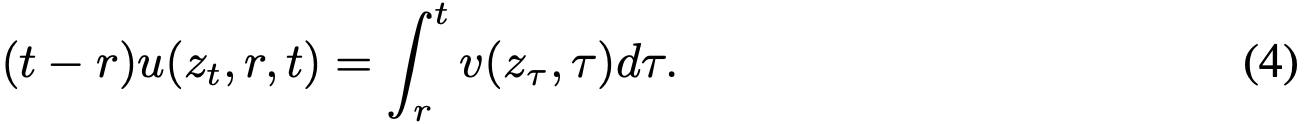
将两边对 t 求导（视 r 独立于 t），得到：
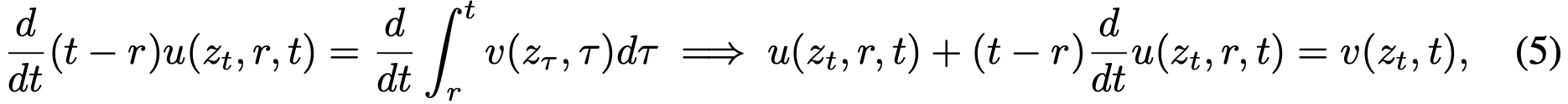
整理后得到恒等式：
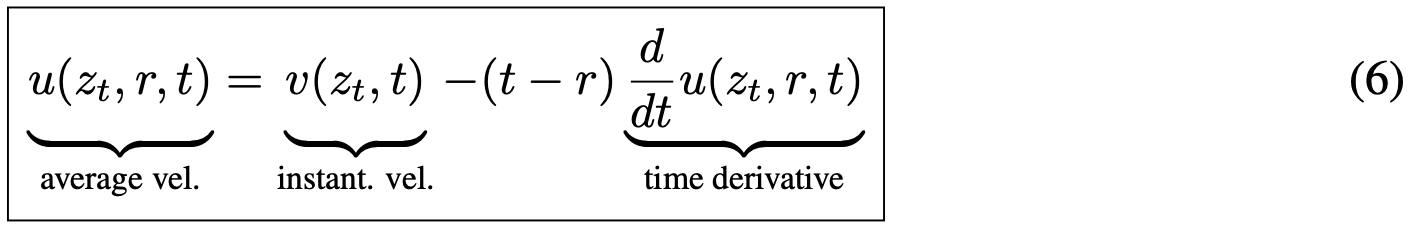
该式称为"MeanFlow 恒等式"，描述了 v 与 u 的关系。式(6)与式(4)的等价性易于证明。
式(6)的右侧为 u(z_t, r, t) 提供了"目标"形式，将用于构建损失函数训练神经网络。为使目标适用，需进一步分解时间导数项。
Computing Time Derivative.
为计算式(6)中的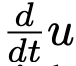 
项，需注意 d/dt 表示全导数，可按偏导数展开：
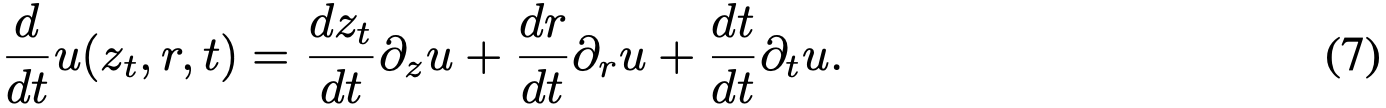
代入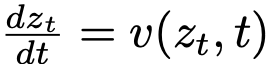 
，
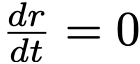和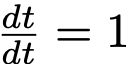 
，得到 u 与 v 的另一关系：
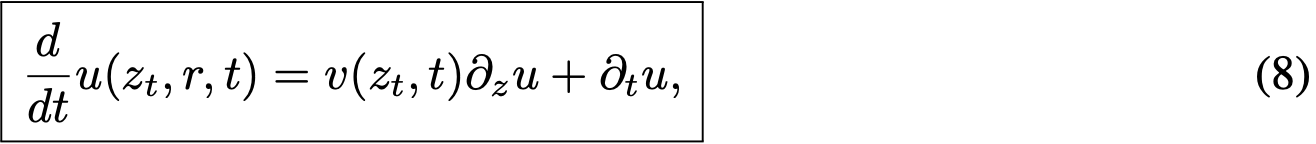
该式表明全导数由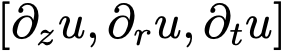 
的雅可比矩阵与切向量 [v, 0, 1] 的雅可比向量积给出。现代计算库可通过 jvp 接口高效计算此值，例如Pytorch的 torch.func.jvp 或JAX的 jax.jvp。
Training with Average Velocity.
至此，所有公式独立于网络参数化。现引入模型以学习 u。具体地，参数化网络 u_θ 并使其满足 MeanFlow 恒等式。通过最小化以下目标实现：
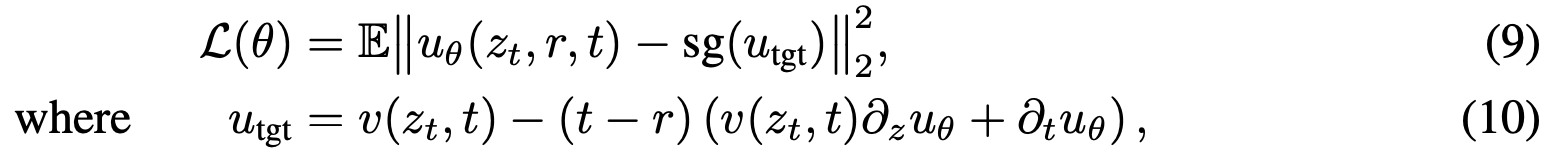
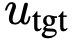作为有效回归目标，由式(6)驱动。该目标仅使用瞬时速度 v 作为真实信号，无需积分计算。虽然目标涉及 u 的导数，但实际使用其参数化版本。损失函数中对目标 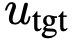应用停止梯度操作，避免通过 JVP 进行双重反向传播，从而规避高阶优化。若 u_θ 达到零损失，则可证明其满足 MeanFlow 恒等式及原始定义。
式(10)中的速度 v(z_t, t) 是流匹配中的边际速度。遵循惯例，将其替换为条件速度。此时目标变为：
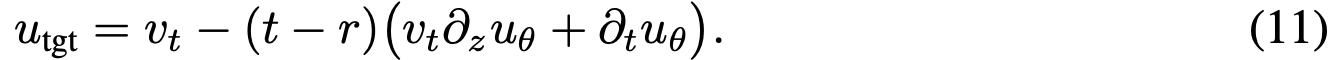
其中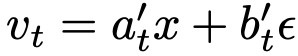 
是条件速度，默认 
。
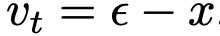最小化损失函数式(9)的伪代码见算法1。该方法概念简洁：行为类似于流匹配，关键区别在于匹配目标被修正项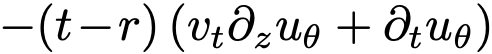 
调整，该修正源于对平均速度的考量。特别地，若限制 t=r，则第二项消失，方法退化为标准流匹配。
算法1中，jvp 操作高效。计算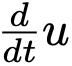 
仅需单次反向传播，与标准反向传播成本相当。由于 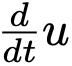是目标 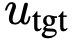的一部分且应用停止梯度，神经网络优化的反向传播将其视为常数，不引入高阶梯度计算。JVP 开销仅增加单次额外反向传播，总训练时间开销低于20%。
Sampling.
使用 MeanFlow 模型采样时，仅需将时间积分替换为平均速度：
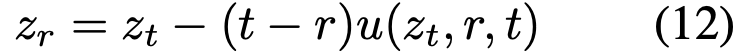
单步采样时，直接计算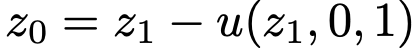 
，其中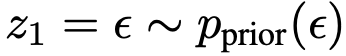 
。算法2给出伪代码。尽管单步采样是重点，该方程同样支持少步采样。
Relation to Prior Work.
本方法与此前单步生成模型相关，但提供了更原理化的框架。核心在于两个底层场 v 与 u 间的泛函关系，自然导出了 u 必须满足的 MeanFlow 恒等式。该恒等式不依赖于神经网络的引入。相比之下，先前工作通常依赖施加于网络行为的额外一致性约束。一致性模型专注于数据端锚定的路径，对应固定 r≡0。因此其条件仅依赖单时间变量。另一方面，Shortcut 和 IMM 模型条件于两个时间变量，引入了额外的双时间自一致性约束。而本方法仅由平均速度定义驱动，用于训练的 MeanFlow 恒等式自然源于该定义，无需额外假设。
4.2 Mean Flows with Guidance
本方法自然支持无分类器引导。不同于在采样时简单应用 CFG（会导致 NFE 翻倍），本方法将 CFG 视为底层真实流场的属性。该表述使方法在保持 1-NFE 采样的同时享受 CFG benefits。
Ground-truth Fields.
构建新真实流场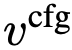 
：
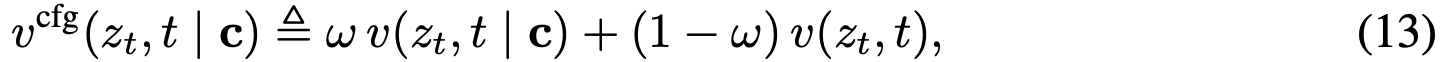
该场是类别条件场与无条件场的线性组合：
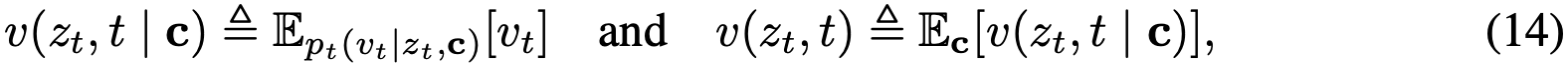
其中 v_t 是条件速度。
基于 MeanFlow 思想，引入对应 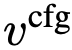的平均速度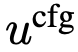 
。根据 MeanFlow 恒等式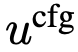， 满足：
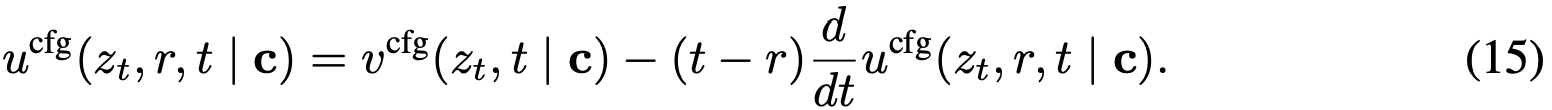
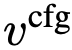与 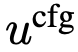是不依赖神经网络的底层真实流场。 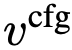可改写为：
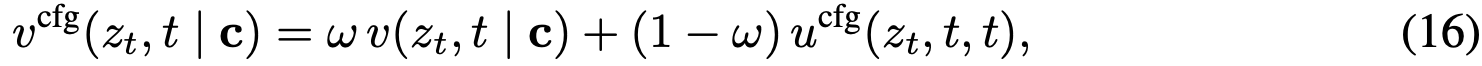
这里保持了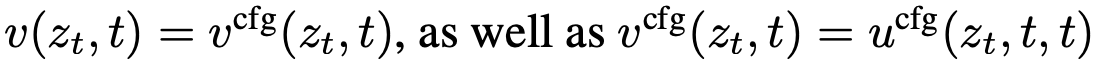
。
Training with Guidance.
基于式(15)与式(16)，构建网络及其学习目标。直接参数化 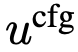为函数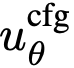 
。基于式(15)，得到目标：
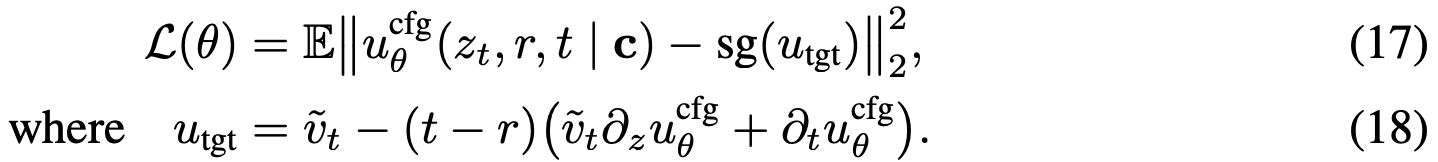
该表述与式(9)类似，唯一区别在于使用了修正的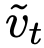 
：
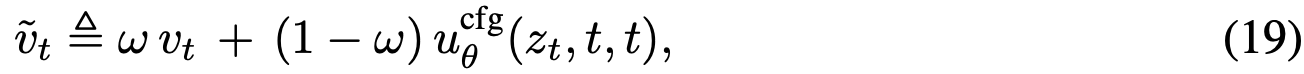
该式由式(16)驱动：式(16)中的边际速度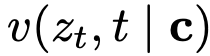 
被替换为条件速度 v_t。若 
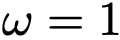，该损失函数退化为无 CFG 情况。
为使网络 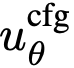接触无条件输入，以10%概率丢弃类别条件。类似地，式(19)中的 
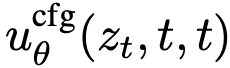也可同时接触无条件与条件版本。
Single-NFE Sampling with CFG.
在本框架中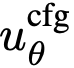， 直接建模由 CFG 速度 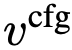诱导的平均速度 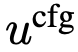。因此采样时无需线性组合：直接使用 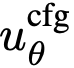进行单步采样，仅需单次 NFE。该表述保持了理想的单 NFE 特性。
4.3 Design Decisions
Loss Metrics.
式(9)使用平方 L2 损失。本文研究不同损失度量。通用形式为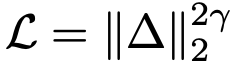 
，其中 Δ 表示回归误差。可证明最小化 
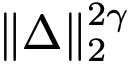等价于最小化带"自适应损失权重"的平方 L2 损失
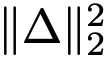。实践中设置权重 
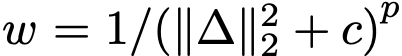，其中 p = 1-γ，c > 0。自适应加权损失为 
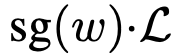，其中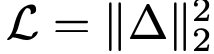 
。若 p=0.5，则类似于伪 Huber 损失。实验比较不同 p 值。
Sampling Time Steps (r,t).
从预定义分布采样两个时间步。研究两种分布：均匀分布 U(0,1) 与 logit-正态分布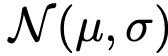
。给定采样对，将较大值赋给 t，较小值赋给 r。设置部分随机样本的 r=t。
Conditioning on (r,t).
使用位置编码编码时间变量，将其组合后作为神经网络的条件输入。需注意，尽管场参数化为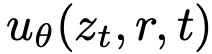 
，网络无需直接条件于 (r, t)。例如，可使网络直接条件于 (t, Δt)，其中 Δt = t - r。此时 
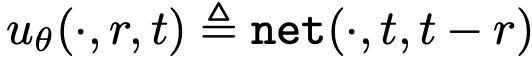，其中 net 是网络。JVP 计算始终关于函数 u_θ(·, r, t)。实验比较不同条件化形式。
5 Experiments
Experiment Setting.
本文主要实验在ImageNet 256×256分辨率上进行生成任务评估。基于5万张生成图像计算Fréchet Inception Distance（FID）指标，重点考察单次函数评估（1-NFE）的生成性能。遵循已有研究范式，模型在预训练VAE编码器的潜空间上实现。对于256×256图像，编码器输出32×32×4的潜表示作为模型输入。所有模型均采用从头训练策略，具体实现细节见附录A。
消融研究中采用ViT-B/4架构（即基础尺寸，补丁大小为4），训练80个周期（40万次迭代）。作为参考，在250-NFE采样下，DiT-B/4的FID为68.4，SiT-B/4（复现结果）为58.9。
5.1 Ablation Study
We investigate the model properties in Tab. 1, analyzed next:
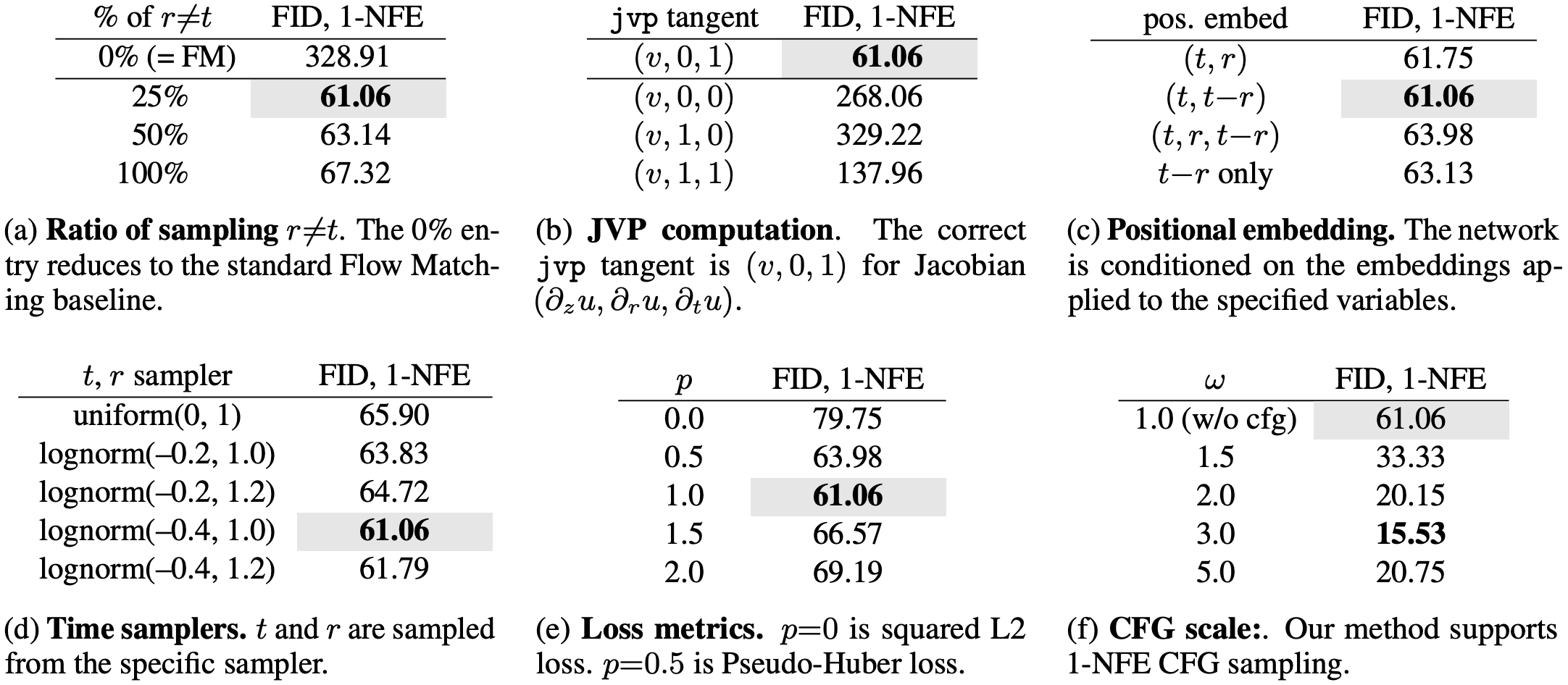
Table 1:Ablation study on 1-NFE ImageNet 256×256 generation. FID-50K is evaluated. Default configurations are marked in gray: B/4 backbone, 80-epoch training from scratch.
From Flow Matching to Mean Flows.
本方法可视为目标函数修正后的流匹配（算法1）。当r恒等于t时，方法退化为标准流匹配。表1(a)显示，r≠t的采样比例对性能影响显著：0%比例（即标准流匹配）在1-NFE生成中完全失效，而非零比例使MeanFlow发挥效用。25%比例取得最优FID，即使100%比例仍能获得有效结果。
JVP Computation.
JVP操作（式8）是连接所有(r,t)坐标的核心关系。表1(b)通过破坏性实验表明，仅当JVP计算正确时才能获得有意义结果。需注意，∂z u方向的JVP切向量为d维（数据维度32×32×4），而∂r u和∂t u方向虽为一维，但对场定义至关重要。
Conditioning on (r,t).
如表1(c)所示，研究不同(r,t)位置编码变体：所有变体均能产生有效的1-NFE结果，证明MeanFlow框架的鲁棒性。其中(t, t−r)编码效果最佳，仅编码间隔t−r也能获得合理结果。
Time Samplers.
先前研究表明时间步采样分布影响生成质量。表1(d)中，对数正态采样器表现最优，与流匹配中的观察一致。采样时先独立抽取(r,t)，后交换确保t>r，并控制r≠t比例。
Loss Metrics.
表1(e)显示自适应损失权重的影响。功率参数p=1时取得最佳结果，p=0.5（类似伪Huber损失）也具有竞争力。标准平方L2损失（p=0）虽表现稍逊，但仍能产生有意义结果。
Guidance Scale.
表1(f)展示CFG的效果：与多步生成一致，CFG在1-NFE设置中显著提升质量。本文的CFG表述天然支持1-NFE采样。
Scalability.
图4展示不同模型规模和训练时长下的1-NFE FID结果。与基于Transformer的扩散/流模型行为一致，MeanFlow在1-NFE生成中展现出良好的扩展性。
5.2 Comparisons with Prior Work
ImageNet 256×256 Comparisons.
如表2（左）所示，MeanFlow大幅超越同类方法：以3.43的FID显著优于IMM的单步结果7.77（相对提升超50%）；若仅比较1-NFE生成，相对先前最佳结果10.60有近70%提升。该方法基本消除了单步与多步扩散/流模型间的性能差距。
在2-NFE生成中，本方法取得2.20的FID（表2左下），与主流多步基线DiT（2.27）和SiT（2.15）相当，而后两者需250×2 NFE。这表明少步扩散/流模型已能媲美多步模型。其他改进技术（如REPA）可作为未来工作。
需特别强调，本方法自成体系且完全从头训练，无需依赖预训练、蒸馏或课程学习即获得强劲结果。
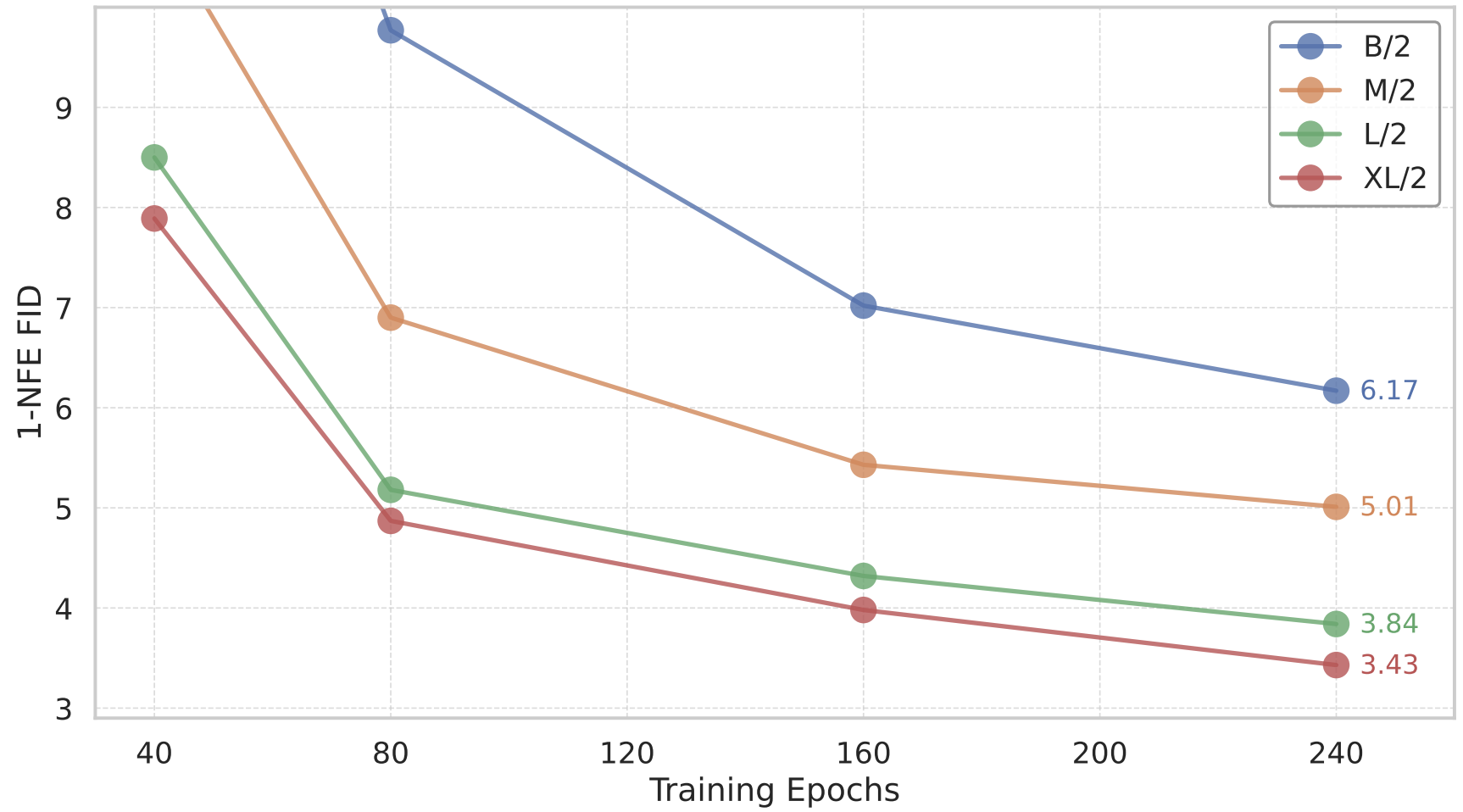
Figure 4:Scalability of MeanFlow models on ImageNet 256×256. 1-NFE generation FID is reported. All models are trained from scratch. CFG is applied while maintaining the 1-NFE sampling behavior. Our method exhibits promising scalability with respect to model size.
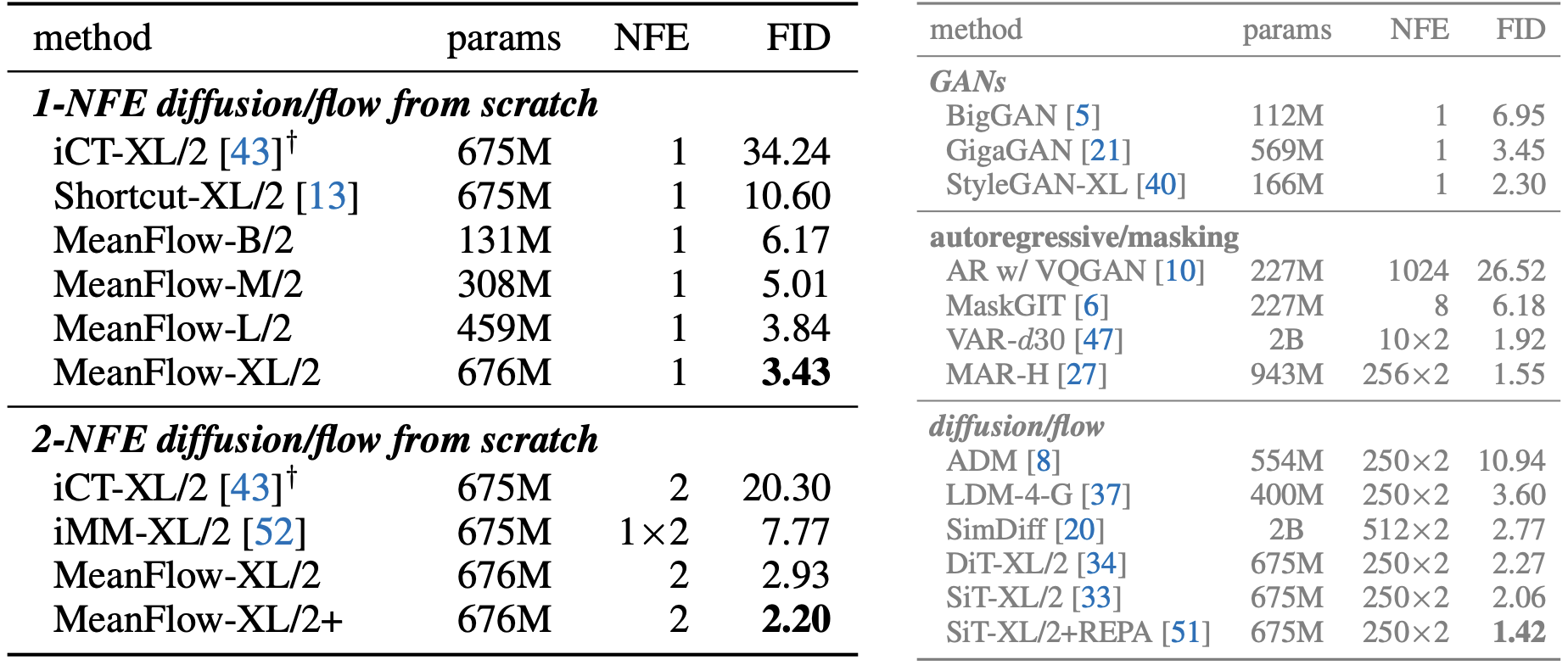
Table 2:Class-conditional generation on ImageNet-256×256. All entries are reported with CFG, when applicable. Left: 1-NFE and 2-NFE diffusion/flow models trained from scratch. Right: Other families of generative models as a reference. In both tables, "×2" indicates that CFG incurs an NFE of 2 per sampling step. Our MeanFlow models are all trained for 240 epochs, except that "MeanFlow-XL+" is trained for more epochs and with configurations selected for longer training, specified in appendix. †: iCT [43] results are reported by [52].
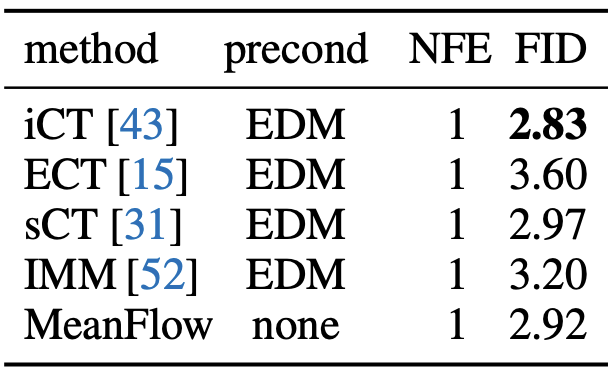
Table 3: Unconditional CIFAR-10.
CIFAR-10 Comparisons.
表3展示CIFAR-10无条件生成结果（1-NFE）。所有对比方法均采用EDM风格预处理，而本方法无需预处理。在该数据集上，本方法与现有方法保持竞争力。