线性代数 · 几何意义 | 基础、向量、行列式与线性方程组（上篇）

注：本文为 "线性代数 · 几何意义" 相关合辑。

图片清晰度受引文原图所限。

略作重排，如有内容异常，请看原文。

受 csdn 篇幅所限分篇。

一、线性代数的基本概念

（一）线性与非线性

线性代数的核心在于研究线性关系。在实际问题中，许多非线性问题可以通过一定的方法转化为线性问题求解，这是线性代数在应用中的重要思路之一。

（二）线性空间

线性空间是线性代数的基础结构之一。线性空间是指满足"加法"和"数乘"两种运算，并遵循八条公理的元素的集合。这些元素通常被称为向量，而运算则在给定的数域 F F F（如实数域 R \mathbb{R} R、复数域 C \mathbb{C} C）上进行。

设 V V V 为非空集合， F F F 为数域。定义 V V V 上的"加法"运算（记为 + + +，即对任意 α , β ∈ V \alpha, \beta \in V α,β∈V，有唯一 γ = α + β ∈ V \gamma = \alpha + \beta \in V γ=α+β∈V）和 F F F 与 V V V 间的"数乘"运算（记为 ⋅ \cdot ⋅，即对任意 k ∈ F k \in F k∈F、 α ∈ V \alpha \in V α∈V，有唯一 δ = k ⋅ α ∈ V \delta = k \cdot \alpha \in V δ=k⋅α∈V）。若两种运算满足以下八条公理，则称 V V V 为 F F F 上的线性空间（或向量空间）：

加法交换律 ：对任意 α , β ∈ V \alpha, \beta \in V α,β∈V，有 α + β = β + α \alpha + \beta = \beta + \alpha α+β=β+α。
加法结合律 ：对任意 α , β , γ ∈ V \alpha, \beta, \gamma \in V α,β,γ∈V，有 ( α + β ) + γ = α + ( β + γ ) (\alpha + \beta) + \gamma = \alpha + (\beta + \gamma) (α+β)+γ=α+(β+γ)。
加法零元存在 ：存在唯一元素 0 ∈ V 0 \in V 0∈V，对任意 α ∈ V \alpha \in V α∈V，有 α + 0 = α \alpha + 0 = \alpha α+0=α。该元素 0 0 0 称为 V V V 的零向量。
加法负元存在 ：对任意 α ∈ V \alpha \in V α∈V，存在唯一元素 β ∈ V \beta \in V β∈V，使得 α + β = 0 \alpha + \beta = 0 α+β=0。该元素 β \beta β 称为 α \alpha α 的负向量，记为 β = − α \beta = -\alpha β=−α。
数乘单位元存在 ：对任意 α ∈ V \alpha \in V α∈V，有 1 ⋅ α = α 1 \cdot \alpha = \alpha 1⋅α=α，其中 1 1 1 是数域 F F F 的乘法单位元。
数乘结合律 ：对任意 k , l ∈ F k, l \in F k,l∈F、 α ∈ V \alpha \in V α∈V，有 k ⋅ ( l ⋅ α ) = ( k ⋅ l ) ⋅ α k \cdot (l \cdot \alpha) = (k \cdot l) \cdot \alpha k⋅(l⋅α)=(k⋅l)⋅α。
数乘对加法的分配律 ：对任意 k ∈ F k \in F k∈F、 α , β ∈ V \alpha, \beta \in V α,β∈V，有 k ⋅ ( α + β ) = k ⋅ α + k ⋅ β k \cdot (\alpha + \beta) = k \cdot \alpha + k \cdot \beta k⋅(α+β)=k⋅α+k⋅β。
加法对数乘的分配律 ：对任意 k , l ∈ F k, l \in F k,l∈F、 α ∈ V \alpha \in V α∈V，有 ( k + l ) ⋅ α = k ⋅ α + l ⋅ α (k + l) \cdot \alpha = k \cdot \alpha + l \cdot \alpha (k+l)⋅α=k⋅α+l⋅α。

线性空间的定义核心是"运算"与"公理"的结合。仅存在元素的集合不足以构成线性空间，必须通过加法和数乘运算定义元素间的关系，并满足上述八条公理，才能形成具有几何意义（如向量叠加、缩放、线性变换）的线性结构。

（三）线性函数

线性函数是线性代数中的重要概念，其几何意义和代数意义如下：

几何意义：线性函数的几何意义表现为过原点的直线、平面或超平面。
代数意义 ：线性函数的代数意义体现在可加性与比例性两个方面。
- 可加性：线性的可加性指的是多个输入量共同作用时，总输出等于各个输入量单独作用时输出的总和。
- 比例性：比例性又名齐次性，其核心是输入量与输出量之间保持倍数关系。例如，在电路系统中，当没有输入量时输出也为零，当输入量变为原来的几倍时，输出量也恰好变为原来的几倍。
数学表达式
y = f ( x ) = K x y = f(x) = Kx y=f(x)=Kx
y = f ( x ) = ( y 1 y 2 ⋮ y m ) , K = [ k 11 k 12 ⋯ k 1 n k 21 k 22 ⋯ k 2 n ⋮ ⋮ ⋱ ⋮ k m 1 k m 2 ⋯ k m n ] , x = ( x 1 x 2 ⋮ x n ) y = f(x) = \begin{pmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \end{pmatrix}, \quad K = \begin{bmatrix} k_{11} & k_{12} & \cdots & k_{1n} \\ k_{21} & k_{22} & \cdots & k_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ k_{m1} & k_{m2} & \cdots & k_{mn} \end{bmatrix}, \quad x = \begin{pmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \end{pmatrix} y=f(x)= y1y2⋮ym ,K= k11k21⋮km1k12k22⋮km2⋯⋯⋱⋯k1nk2n⋮kmn ,x= x1x2⋮xn
其中， y y y 为 m m m 维输出向量， x x x 为 n n n 维输入向量， K K K 为 m × n m \times n m×n 维系数矩阵。
几何意义补充 ：当 m = n m = n m=n 时，线性函数对应的几何图形为直线；当 m ≠ n m \neq n m=n 时，线性函数对应的几何图形为平面或超平面。

（四）线性映射

线性映射是线性代数中的另一个重要概念，其基本性质如下：

基本性质
线性映射满足以下两个基本性质：
T ( α + β ) = T α + T β T ( k α ) = k T α T(\alpha + \beta) = T\alpha + T\beta\\ T(k\alpha) = kT\alpha T(α+β)=Tα+TβT(kα)=kTα
其中， α \alpha α、 β \beta β 是线性空间中的向量， k k k 是数域中的常数， T T T 在此处也被称为线性算子。
常见的线性算子包括微分算子、积分算子、拉普拉斯算子等，这些算子在数学分析、物理等领域有着广泛的应用。
二维线性映射 ：二维线性函数会构成两个二维平面之间的映射关系，该映射关系由矩阵 K = [ a 1 a 2 b 1 b 2 ] K = \begin{bmatrix} a_{1} & a_{2} \\ b_{1} & b_{2} \end{bmatrix} K=[a1b1a2b2] 确定，且满足以下两个条件：
- 映射关系满足可加性和比例性，符合线性映射的基本定义；
- 该映射实现了两个不同坐标系之间的转换，将一个二维坐标系中的向量映射到另一个二维坐标系中。

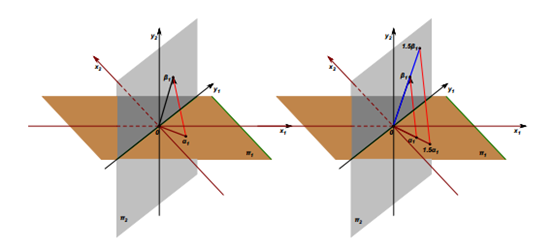
（五）线性变换

线性变换是线性映射的特例，其定义和性质如下：

定义：若线性映射发生在一个集合上的同一个坐标系中，那么这种线性映射就被称为线性变换。线性变换是线性映射的特例，其本质是将集合上原本可能存在的两个坐标系合并为一个坐标系。
示例：在直角坐标系下，通过线性变换可将一个圆形转化为一个椭圆，其中圆上的任意一个向量 α \alpha α，经过线性变换后会映射为椭圆上的对应向量 β \beta β。
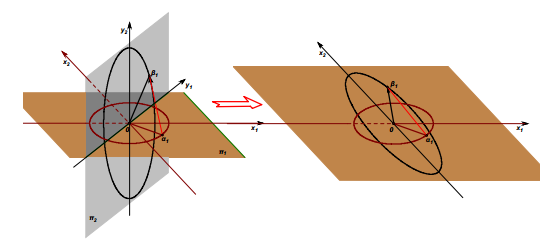
严格定义 ：设 V V V 是数域 F F F 上的线性空间， T T T 是 V V V 到自身的一个变换。若对于任意 α , β ∈ V \alpha, \beta \in V α,β∈V 和任意 k ∈ F k \in F k∈F，都满足以下两个条件：
T ( α + β ) = T α + T β T ( k α ) = k T α T(\alpha + \beta) = T\alpha + T\beta\\ T(k\alpha) = kT\alpha T(α+β)=Tα+TβT(kα)=kTα
则称 T T T 为 V V V 上的线性变换。
性质：与线性映射类似，线性变换能够将向量映射为另一个向量，或者说将"线"映射为"线"。在平面内，线性变换具有以下明确特性：
- 原点经过线性变换后仍映射为原点，即零点位置保持不变；
- 直线经过线性变换后仍映射为直线，不会发生弯曲；
- 平行线经过线性变换后仍保持平行关系；
- 平行四边形经过线性变换后仍映射为平行四边形。

二、向量的基本几何意义

（一）自由向量

自由向量具有大小和方向两个基本属性，这与物理学中的矢量概念一致。自由向量的特点是可以在空间中自由平移，平移后其大小和方向保持不变，仅位置发生改变。

（二）向量的数学表示

为了便于数学分析，可将空间中所有向量的尾部都平移至坐标原点，此时 N N N 维点空间与 N N N 维向量空间能够建立一一对应关系。具体来说，在 N N N 维点空间中，取点 ( 0 , 0 , 0 , ⋯ , 0 ) (0, 0, 0, \cdots, 0) (0,0,0,⋯,0) 作为原点，那么空间中的每一个点都可以与一个向量相对应，这个向量就是从坐标原点出发并指向该点的有向线段。

（三）向量加法的几何与物理意义

几何意义 ：向量加法遵循平行四边形法则和三角形法则。
- 平行四边形法则：以两个向量为邻边作平行四边形，从共同起点出发的对角线所对应的向量即为两个向量的和。
- 三角形法则：将第二个向量的起点与第一个向量的终点重合，从第一个向量的起点指向第二个向量的终点的向量即为两个向量的和。
物理意义：以船过河问题为例，船在河中行驶时，其实际位移由三个部分组成：一是船头的位移，由马达动力提供；二是流水影响的位移，由水流速度产生；三是船的真正位移，即前两个位移的向量和，该实例直观地体现了向量加法的物理意义。

（四）向量内积

数学表达式
向量内积有两种常见的数学表达式，分别从几何和代数角度描述内积运算：
a ⋅ b = ∣ a ∣ ∣ b ∣ cos ⁡ θ a ⋅ b = a x b x + a y b y + a z b z \begin{align} a \cdot b &= |a||b|\cos\theta \tag{1} \\ a \cdot b &= a_{x}b_{x} + a_{y}b_{y} + a_{z}b_{z} \tag{2} \end{align} a⋅ba⋅b=∣a∣∣b∣cosθ=axbx+ayby+azbz(1)(2)
其中，式（1）中 ∣ a ∣ |a| ∣a∣、 ∣ b ∣ |b| ∣b∣ 分别表示向量 a a a、 b b b 的模长， θ \theta θ 表示向量 a a a、 b b b 之间的夹角；
式（2）中 a x , a y , a z a_{x}, a_{y}, a_{z} ax,ay,az 和 b x , b y , b z b_{x}, b_{y}, b_{z} bx,by,bz 分别表示向量 a a a、 b b b 在 x x x、 y y y、 z z z 轴上的坐标分量。
定义解读
- 几何角度 ：向量 a a a 和 b b b 的内积等于两向量模长的乘积再乘以它们之间夹角的余弦值，该表达式直接反映了向量内积与向量长度、夹角之间的关系。
- 代数角度 ：向量 a a a 和 b b b 的内积等于两向量对应坐标分量乘积的和，该表达式为向量内积的计算提供了具体的代数方法。
几何与物理意义
- 几何意义 ：向量内积的几何解释是一个向量在另一个向量上的投影与被投影向量模长的乘积，即同方向上的乘积。特别地，若向量 a a a 是某一坐标轴的单位坐标向量，那么向量 a a a 与向量 b b b 的内积 a ⋅ b a \cdot b a⋅b 就等于向量 b b b 在该坐标轴上的坐标值，这一结论是傅立叶分析的重要理论基础。此外，通过向量内积的数值还可以判断两个向量在方向上的接近程度：
  - 当内积值为正值时，两个向量大致指向相同的方向，此时两向量夹角小于 9 0 ∘ 90^\circ 90∘；
  - 当内积值为负值时，两个向量大致指向相反的方向，此时两向量夹角大于 9 0 ∘ 90^\circ 90∘；
  - 当内积值为 0 0 0 时，两个向量互相垂直，此时两向量夹角等于 9 0 ∘ 90^\circ 90∘。
- 生活解释 ：在日常生活中，单价向量与数量向量的内积即为总价格。例如，若某商品单价向量为 ( p 1 , p 2 ) (p_1, p_2) (p1,p2)（ p 1 p_1 p1、 p 2 p_2 p2 分别为两种商品的单价），购买数量向量为 ( q 1 , q 2 ) (q_1, q_2) (q1,q2)（ q 1 q_1 q1、 q 2 q_2 q2 分别为两种商品的购买数量），则总价格为 p 1 q 1 + p 2 q 2 p_1q_1 + p_2q_2 p1q1+p2q2，即两个向量的内积。
- 物理解释 ：在物理学中，向量内积可用于计算力所做的功。例如，在斜坡上用 force F F F 斜向上拉一个物体，若物体的位移为 S S S（不考虑重力作用），则力 F F F 所做的功 W W W 为：
  W = F s ⋅ S = ∣ F ∣ ∣ S ∣ cos ⁡ θ W = F_s \cdot S = |F||S|\cos\theta W=Fs⋅S=∣F∣∣S∣cosθ
  其中， θ \theta θ 是力 F F F 与位移 S S S 之间的夹角。

（五）向量的外积（叉积）

数学表达式 ：设三维空间中的两个向量分别为 a = ( a x , a y , a z ) a = (a_{x}, a_{y}, a_{z}) a=(ax,ay,az) 和 b = ( b x , b y , b z ) b = (b_{x}, b_{y}, b_{z}) b=(bx,by,bz)，则向量 a a a 与 b b b 的外积（叉积）表达式为：
a × b = ( a y b z − a z b y a z b x − a x b z a x b y − a y b x ) a \times b = \begin{pmatrix} a_{y}b_{z} - a_{z}b_{y} \\ a_{z}b_{x} - a_{x}b_{z} \\ a_{x}b_{y} - a_{y}b_{x} \end{pmatrix} a×b= aybz−azbyazbx−axbzaxby−aybx

同时，向量外积也可以表示为：
a × b = ∣ a ∣ ∣ b ∣ sin ⁡ θ ⋅ N a \times b = |a||b|\sin\theta \cdot N a×b=∣a∣∣b∣sinθ⋅N

其中， ∣ a ∣ |a| ∣a∣、 ∣ b ∣ |b| ∣b∣ 分别为向量 a a a、 b b b 的模长， θ \theta θ 为向量 a a a、 b b b 之间的夹角， N N N 为垂直于向量 a a a 和 b b b 所展成平面的单位向量，其方向由右手定则确定。
几何与物理意义
- 几何意义 ：向量 a a a 与 b b b 的外积 a × b a \times b a×b 是一个新生成的向量，该向量垂直于由向量 a a a 和 b b b 展成的平面（即由线段 o a oa oa 和 o b ob ob 所确定的平面）；同理，向量 b b b 与 a a a 的外积 b × a b \times a b×a 也垂直于该平面，但方向与 a × b a \times b a×b 相反，即满足 a × b = − b × a a \times b = -b \times a a×b=−b×a。判断 a × b a \times b a×b 方向的右手定则为：将右手四指从向量 a a a 指向向量 b b b（沿小于 18 0 ∘ 180^\circ 180∘ 的角转动），此时大拇指所指的方向即为 a × b a \times b a×b 的方向。
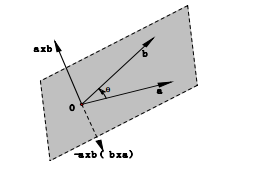
- 物理意义 ：向量外积在物理学中被称为轴向量，具有明确的物理应用场景，具体包括：
  1. 陀螺定向 ：高速旋转的陀螺具有定向特性，其定向方向与矢径向量 r r r 和线速度向量 v v v 的叉乘结果（角速度 ω \omega ω）方向一致。正是由于这种特性，陀螺常被用于导航、姿态控制等领域。
  2. 螺钉运动 ：螺钉通过左右旋转可在螺孔中实现前进或后退。以右螺旋螺钉为例，用螺丝刀沿 F + F_+ F+ 方向右旋螺钉时，扭力向量 F F F 与矢径向量 r r r 的叉乘结果即为力矩 M M M 的方向，螺钉会沿着力矩 M M M 的方向在螺母孔内前进；若反向旋转螺钉，则叉积方向改变，螺钉随之退出螺孔。这表明力矩（叉乘向量）的方向与螺钉螺旋前进的方向一致，且垂直于螺丝刀口和扭力的方向，即垂直于被叉乘的两个向量的方向。
  3. 自行车平衡：自行车静止时，人坐在车上容易摔倒；而当自行车骑行起来后，车子会保持平稳且不易左右倾倒，这一现象的本质与陀螺原理相同，均是向量外积的作用结果。骑行时，车轮的旋转产生了角动量，角动量的方向由车轮旋转的线速度向量与车轮半径向量（矢径向量）的叉乘确定，角动量的守恒性使得自行车能够保持平衡。

（六）向量混合运算的几何意义

向量加法结合律

向量加法结合律的数学表达式为：
( a + b ) + c = a + ( b + c ) (a + b) + c = a + (b + c) (a+b)+c=a+(b+c)

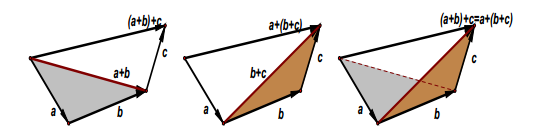
几何解释：从几何图形上可以直观地观察到，先将向量 a a a 与向量 b b b 相加得到向量 a + b a + b a+b，再将其与向量 c c c 相加，得到的结果向量 ( a + b ) + c (a + b) + c (a+b)+c；与先将向量 b b b 与向量 c c c 相加得到向量 b + c b + c b+c，再将其与向量 a a a 相加得到的结果向量 a + ( b + c ) a + (b + c) a+(b+c)，两者的终点完全重合，这表明向量加法满足结合律。
向量数乘分配律

向量数乘分配律的数学表达式为：
k ( a + b ) = k a + k b k(a + b) = ka + kb k(a+b)=ka+kb

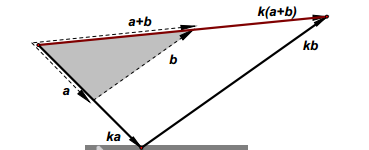
几何解释：在平面直角坐标系中，将向量 a + b a + b a+b 乘以常数 k k k 得到的向量 k ( a + b ) k(a + b) k(a+b)，与将向量 a a a、 b b b 分别乘以常数 k k k 得到向量 k a ka ka、 k b kb kb，再将 k a ka ka 与 k b kb kb 相加得到的向量 k a + k b ka + kb ka+kb 完全重合，这一几何现象验证了向量数乘分配律的成立。
向量点积分配律

向量点积分配律的数学表达式为：
a ⋅ ( b + c ) = a ⋅ b + a ⋅ c a \cdot (b + c) = a \cdot b + a \cdot c a⋅(b+c)=a⋅b+a⋅c

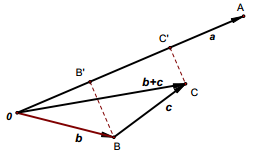
几何解释：根据向量点积的几何意义，向量 b + c b + c b+c 在向量 a a a 上的投影等于向量 b b b 在向量 a a a 上的投影与向量 c c c 在向量 a a a 上的投影之和。结合向量点积"投影与被投影向量模长的乘积"这一几何定义，可推出向量 a a a 与向量 b + c b + c b+c 的点积等于向量 a a a 与向量 b b b 的点积加上向量 a a a 与向量 c c c 的点积，从而证明向量点积分配律成立。
向量叉积分配律

向量叉积分配律的数学表达式为：
( a + b ) × c = a × c + b × c (a + b) \times c = a \times c + b \times c (a+b)×c=a×c+b×c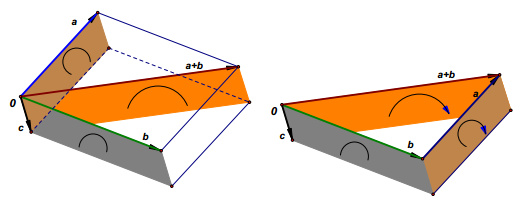

几何解释：从几何角度来看，向量的有向面积满足平行四边形法则和三角形法则。向量 ( a + b ) (a + b) (a+b) 与向量 c c c 的叉积对应的有向面积，等于向量 a a a 与向量 c c c 的叉积对应的有向面积加上向量 b b b 与向量 c c c 的叉积对应的有向面积，通过有向面积的叠加关系可验证向量叉积分配律。
向量混合积
- 基本关系 ：三向量的混合积满足轮换对称性，即
  ( a × b ) ⋅ c = ( b × c ) ⋅ a = ( c × a ) ⋅ b (a \times b) \cdot c = (b \times c) \cdot a = (c \times a) \cdot b (a×b)⋅c=(b×c)⋅a=(c×a)⋅b；
  同时，混合积还可以表示为
  ( a × b ) ⋅ c = ∣ a × b ∣ ∣ c ∣ cos ⁡ α (a \times b) \cdot c = |a \times b||c|\cos\alpha (a×b)⋅c=∣a×b∣∣c∣cosα，
  其中 α \alpha α 为向量 a × b a \times b a×b 与向量 c c c 之间的夹角。

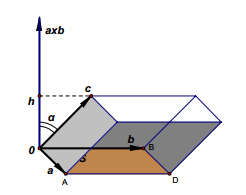
几何解释 ：以向量 a a a、 b b b、 c c c 为棱可以构成一个平行六面体，该平行六面体底面（由向量 a a a、 b b b 构成的平行四边形 O A D B OADB OADB）的面积 S S S 在数值上等于向量 a a a 与 b b b 外积的模长 ∣ a × b ∣ |a \times b| ∣a×b∣；平行六面体的高 h h h 等于向量 c c c 在向量 a × b a \times b a×b 上的投影，即 h = ∣ c ∣ cos ⁡ α h = |c|\cos\alpha h=∣c∣cosα。根据平行六面体体积公式 V = S ⋅ h V = S \cdot h V=S⋅h，可推出其体积为：
V = S ⋅ h = ∣ a × b ∣ ∣ c ∣ cos ⁡ α V = S \cdot h = |a \times b||c|\cos\alpha V=S⋅h=∣a×b∣∣c∣cosα
这表明三向量的混合积在数值上等于以这三个向量为棱的平行六面体的体积。

（七）向量的投影和几何解释

多个向量在任意轴上的投影和：多个或有限个向量的和在任意轴上的投影，等于各个向量在同一轴上投影的和。
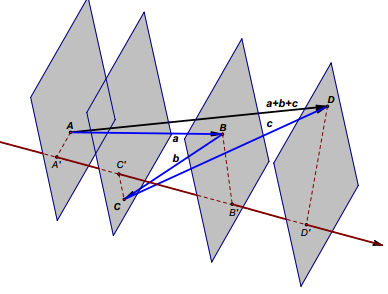
- 示例：在某一轴上，向量 a a a 的投影为 A ′ B ′ A'B' A′B′，向量 b b b 的投影为 B ′ C ′ B'C' B′C′，向量 c c c 的投影为 C ′ D ′ C'D' C′D′，则向量 a + b + c a + b + c a+b+c 的投影为 A ′ D ′ A'D' A′D′，且满足 A ′ B ′ + B ′ C ′ + C ′ D ′ = A ′ D ′ A'B' + B'C' + C'D' = A'D' A′B′+B′C′+C′D′=A′D′，该实例直观地验证了这一结论。
多个向量在任意平面上的投影和：多个或有限个向量的和在任意平面上的投影，等于各个向量在同一平面上投影的和。
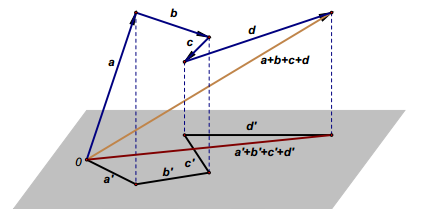
- 几何解释：将各个向量分别投影到指定平面上，得到对应的投影向量；将这些投影向量相加，其结果与先将原向量相加得到和向量，再将和向量投影到该平面上得到的投影向量完全相同，这一几何关系证明了该结论的正确性。

（八）变向量的几何意义

对于用数组 ( a 1 , a 2 , ⋯ , a n ) (a_{1}, a_{2}, \cdots, a_{n}) (a1,a2,⋯,an) 表示的向量 a a a，若数组中的元素部分或全部为变量，则该向量称为变向量。变向量在 n n n 维坐标系下会对应特定的几何图形，具体情况如下：

二维变向量的几何图形

在二维坐标系中，不同形式的变向量对应不同的几何图形：
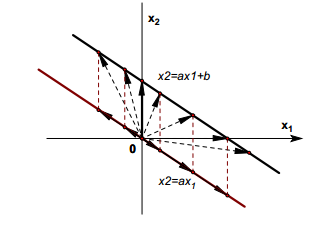
- 变向量 ( x 1 , x 2 ) (x_{1}, x_{2}) (x1,x2) 中， x 1 x_{1} x1 和 x 2 x_{2} x2 均为独立变量，其对应的几何图形为整个二维平面；
- 变向量 ( x 1 , a 2 ) (x_{1}, a_{2}) (x1,a2) 中， x 1 x_{1} x1 为变量， a 2 a_{2} a2 为常数，其对应的几何图形为平行于 x 1 x_1 x1 轴的直线 x 2 = a 2 x_{2} = a_{2} x2=a2；
- 变向量 ( x 1 , a x 1 + b ) (x_{1}, ax_{1} + b) (x1,ax1+b) 中， x 1 x_{1} x1 为变量， a a a、 b b b 为常数，其对应的几何图形为斜率为 a a a、截距为 b b b 的直线 x 2 = a x 1 + b x_{2} = ax_{1} + b x2=ax1+b；
- 变向量 ( x 1 , a x 1 ) (x_{1}, ax_{1}) (x1,ax1) 中， x 1 x_{1} x1 为变量， a a a 为常数，其对应的几何图形为过坐标原点、斜率为 a a a 的直线。
- 分解关系：变向量 ( x 1 , a x 1 + b ) (x_{1}, ax_{1} + b) (x1,ax1+b) 可分解为 ( x 1 , a x 1 ) + ( 0 , b ) (x_{1}, ax_{1}) + (0, b) (x1,ax1)+(0,b)。从向量角度解释，变向量 ( x 1 , a x 1 + b ) (x_{1}, ax_{1} + b) (x1,ax1+b) 是变向量 ( x 1 , a x 1 ) (x_{1}, ax_{1}) (x1,ax1) 与常向量 ( 0 , b ) (0, b) (0,b) 的和；从图形角度解释，直线 x 2 = a x 1 + b x_{2} = ax_{1} + b x2=ax1+b 是由过原点的直线 x 2 = a x 1 x_{2} = ax_{1} x2=ax1 沿向量 ( 0 , b ) (0, b) (0,b) 的方向平移 ∣ b ∣ |b| ∣b∣ 个单位得到的。
三维变向量的几何图形

在三维坐标系中，变向量的形式不同，对应的几何图形也不同：
- 变向量 ( x 1 , x 2 , a x 1 + b x 2 ) (x_{1}, x_{2}, ax_{1} + bx_{2}) (x1,x2,ax1+bx2) 中， x 1 x_{1} x1、 x 2 x_{2} x2 为独立变量， a a a、 b b b 为常数，可对其进行向量分解：
  ( x 1 , x 2 , a x 1 + b x 2 ) = ( x 1 , 0 , a x 1 ) + ( 0 , x 2 , b x 2 ) = x 1 ( 1 , 0 , a ) + x 2 ( 0 , 1 , b ) (x_{1}, x_{2}, ax_{1} + bx_{2}) = (x_{1}, 0, ax_{1}) + (0, x_{2}, bx_{2}) = x_{1}(1, 0, a) + x_{2}(0, 1, b) (x1,x2,ax1+bx2)=(x1,0,ax1)+(0,x2,bx2)=x1(1,0,a)+x2(0,1,b)
  该变向量对应的几何图形是一个向量空间，具体为由常向量 ( 1 , 0 , a ) (1, 0, a) (1,0,a) 和 ( 0 , 1 , b ) (0, 1, b) (0,1,b) 张成的向量平面空间，记为 Span { ( 1 , 0 , a ) , ( 0 , 1 , b ) } \text{Span}\{(1, 0, a), (0, 1, b)\} Span{(1,0,a),(0,1,b)}，因此存在等价关系：
  ( x 1 , x 2 , a x 1 + b x 2 ) ≅ Span { ( 1 , 0 , a ) , ( 0 , 1 , b ) } (x_{1}, x_{2}, ax_{1} + bx_{2}) \cong \text{Span}\{(1, 0, a), (0, 1, b)\} (x1,x2,ax1+bx2)≅Span{(1,0,a),(0,1,b)}
- 变向量 ( x 1 , x 2 , a x 1 + b x 2 + c ) (x_{1}, x_{2}, ax_{1} + bx_{2} + c) (x1,x2,ax1+bx2+c) 中， x 1 x_{1} x1、 x 2 x_{2} x2 为独立变量， a a a、 b b b、 c c c 为常数，第三个变元 x 3 x_3 x3 与 x 1 x_1 x1 、 x 2 x_2 x2 有线性关系： x 3 = a x 1 + b x 2 + c x_3 = ax_1 + bx_2 + c x3=ax1+bx2+c。对其进行向量分解可得：
  ( x 1 , x 2 , a x 1 + b x 2 + c ) = ( x 1 , 0 , a x 1 ) + ( 0 , x 2 , b x 2 ) + ( 0 , 0 , c ) = x 1 ( 1 , 0 , a ) + x 2 ( 0 , 1 , b ) + ( 0 , 0 , c ) (x_{1}, x_{2}, ax_{1} + bx_{2} + c) = (x_{1}, 0, ax_{1}) + (0, x_{2}, bx_{2}) + (0, 0, c) = x_{1}(1, 0, a) + x_{2}(0, 1, b) + (0, 0, c) (x1,x2,ax1+bx2+c)=(x1,0,ax1)+(0,x2,bx2)+(0,0,c)=x1(1,0,a)+x2(0,1,b)+(0,0,c)
  该变向量对应的几何图形仍为一个平面，但与变向量 ( x 1 , x 2 , a x 1 + b x 2 ) (x_{1}, x_{2}, ax_{1} + bx_{2}) (x1,x2,ax1+bx2) 对应的平面相比，其位置沿向量 ( 0 , 0 , c ) (0, 0, c) (0,0,c) 的方向平移了 ∣ c ∣ |c| ∣c∣ 个单位。
变向量与方程的关系 ：一个变向量可以与一个解析方程或方程组相对应，因此变向量和方程一样，都能够表示几何图形。

从函数角度来看，变向量也被称为向量函数，它将变量映射为向量，进而通过向量的几何意义呈现出对应的图形。

线性代数 · 几何意义 | 基础、向量、行列式与线性方程组（下篇）-CSDN博客
https://blog.csdn.net/u013669912/article/details/153281062

参考资料

【线性代数的几何意义】什么是线性代数 - AndyJee - 博客园 posted @ 2013-12-25 21:57 AndyJee
https://www.cnblogs.com/AndyJee/p/3491443.html
【线性代数的几何意义】向量的基本几何意义 - AndyJee - 博客园 posted @ 2013-12-25 22:04 AndyJee
https://www.cnblogs.com/AndyJee/p/3491458.html
【线性代数的几何意义】行列式的几何意义 - AndyJee - 博客园 posted @ 2013-12-25 22:17 AndyJee
https://www.cnblogs.com/AndyJee/p/3491487.html