1. 二叉搜索树介绍
今天来谈一下搜索二叉树，首先复习一下二叉树：它最多有两个孩子(度最多为2的树)。搜索二叉树是在该基础上加了一个特征：左子树的所有结点都小于根，右子树的所有结点都大于根，左右子树都满足以上条件：
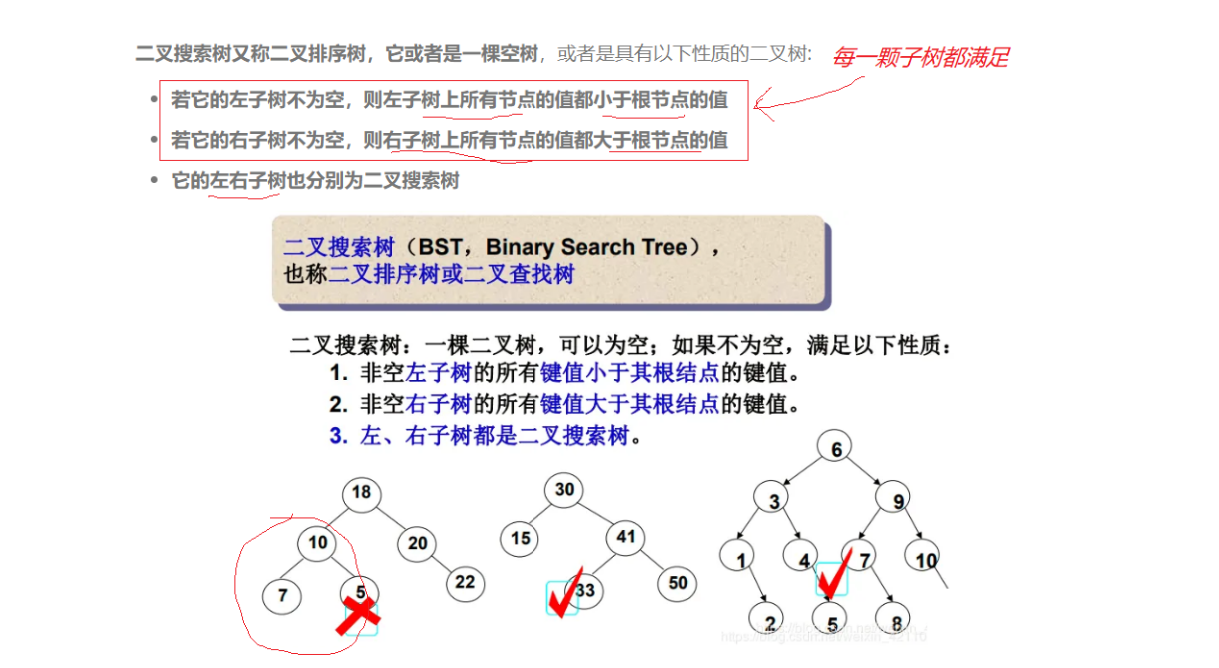
为啥叫搜索二叉树呢？左边比它小，右边比它大，这个东西天生方便搜索。比如上图中第三个树中要找7，7比6大就没必要在左树找；到右树去找，7比9小，没必要去右树找，在左树找。这里最多找高度次就可以找到，很多人会认为时间复杂度是O(logN)，这样是理想化的情况(满二树或完全二叉树)，因为可能会遇到这样的树：
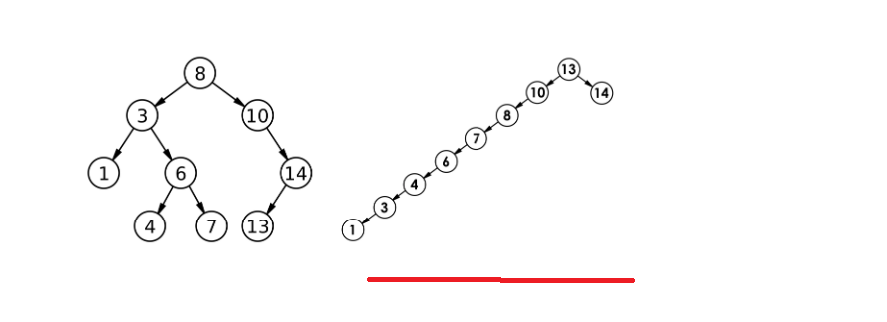
这也是一个搜索二叉树，此时的时间复杂度是O(N)。搜索二叉树也称二叉搜索树或二叉排序树，为啥叫二叉排序树？可以走中序试一试，发现是有序的。
2.二叉搜索树的实现
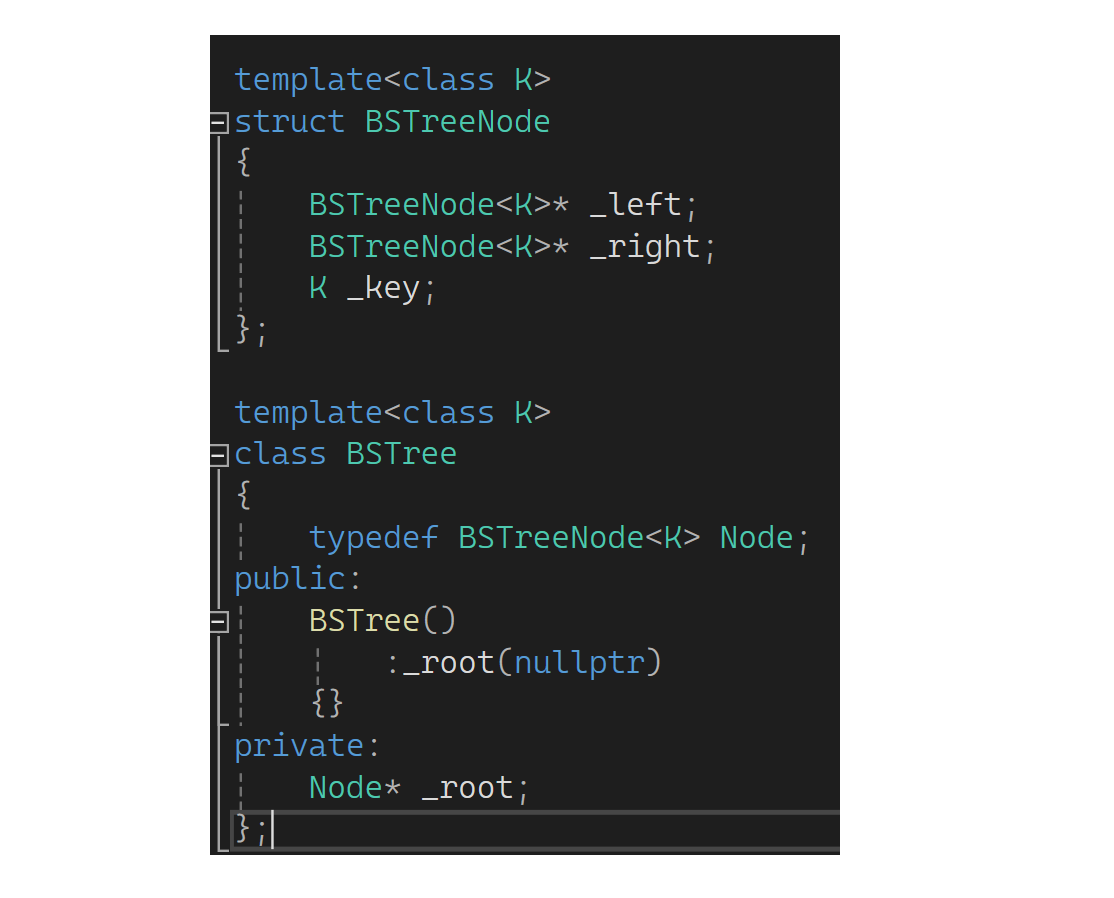
下面直接来实现(因为前面博客有详细介绍二叉树，这里直接搭起框架，不同的是结点用struct，以便后面使用)：
先来写一个Insert，比如插入这样一些值：
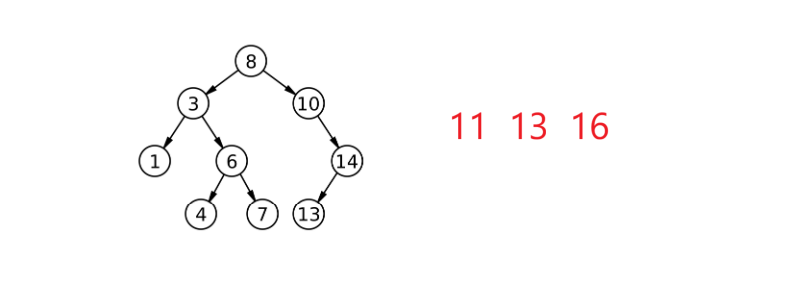
依次比着找：11比8大，比10大，比14小，比13小，找到一个空位置可完成插入；13经过找位置发现已经有了，插入失败；16比8大，比10大，比14大，找到空位插入：
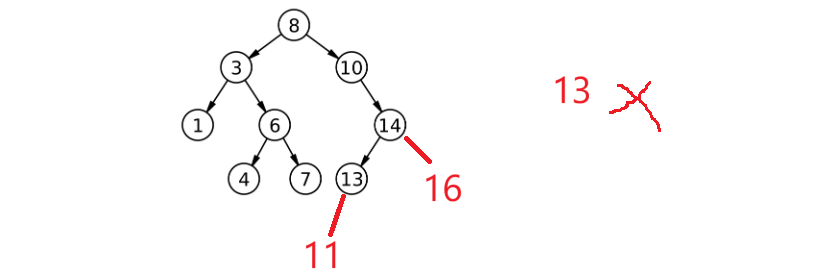
下面来实现，如果这棵树是空树，直接new一个给他就可以了，返回一个true；不是空树。先找位置，若插入值比当前位置大，就往右边走；若插入值比当前位置小，就往左边走；相等就返回false。当cur到空找到合适位置后，想链接还需要增加parent，每次更新cur和parent。此时不知道在哪边，最后再判断比一下：
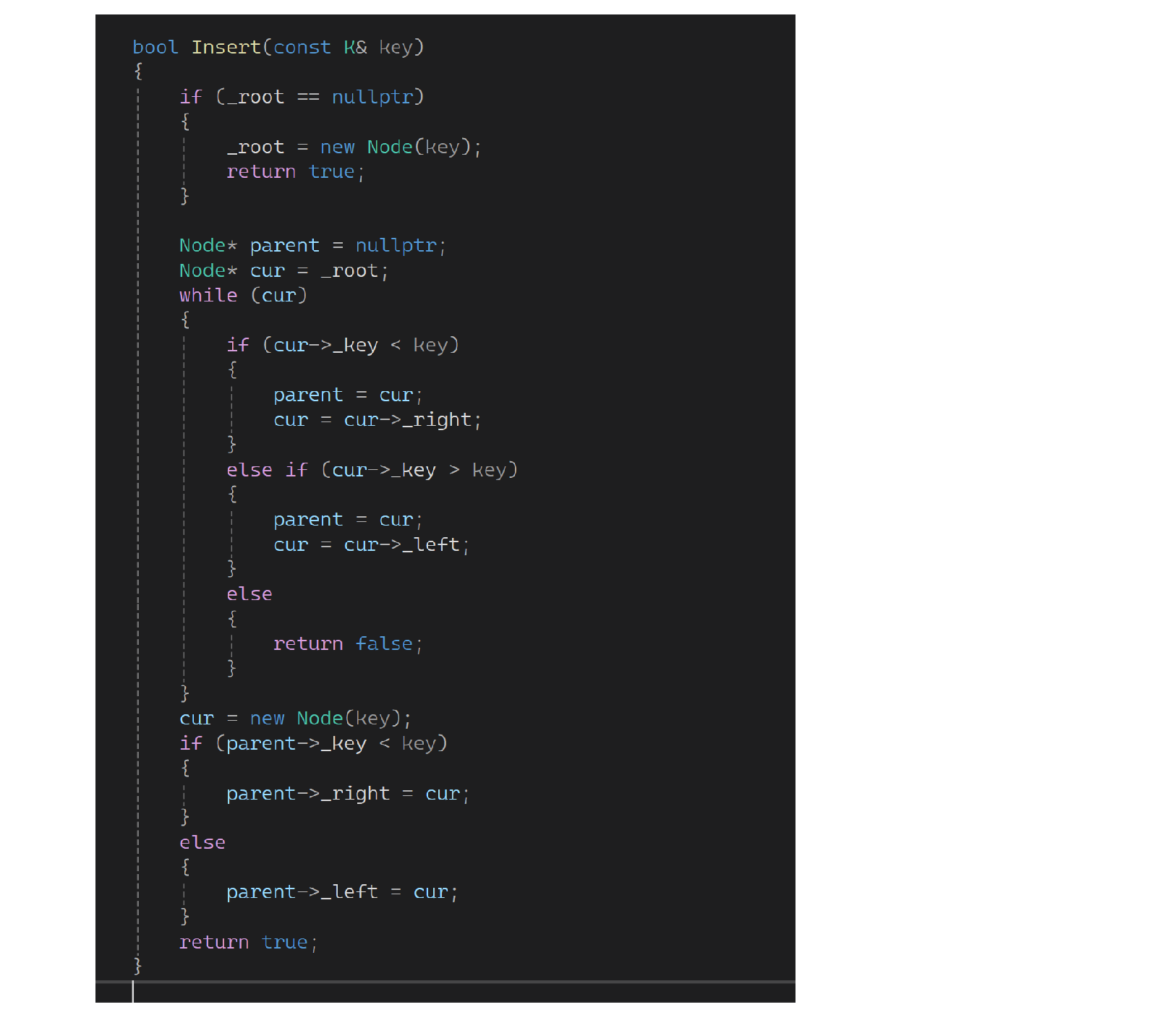
再来实现一个中序方便后面调试看：
下面走一颗数试一试：
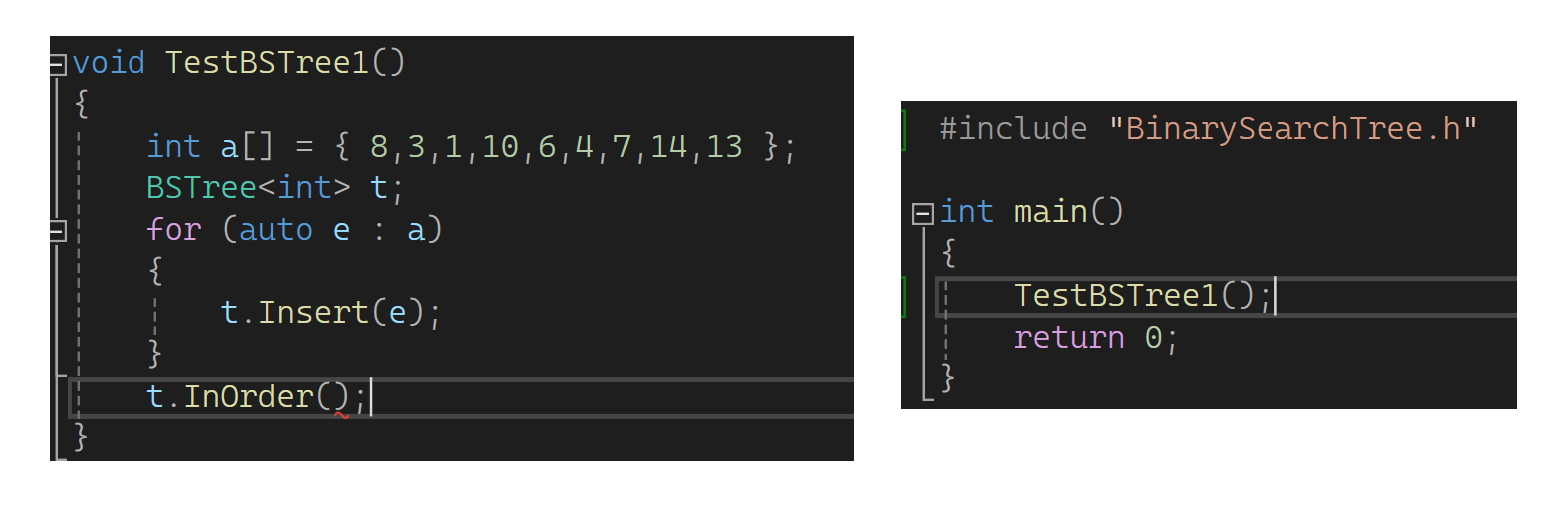
直接这样不太好调用，要传参数，最便捷的方式是再套一层(顺便补一下构造)：
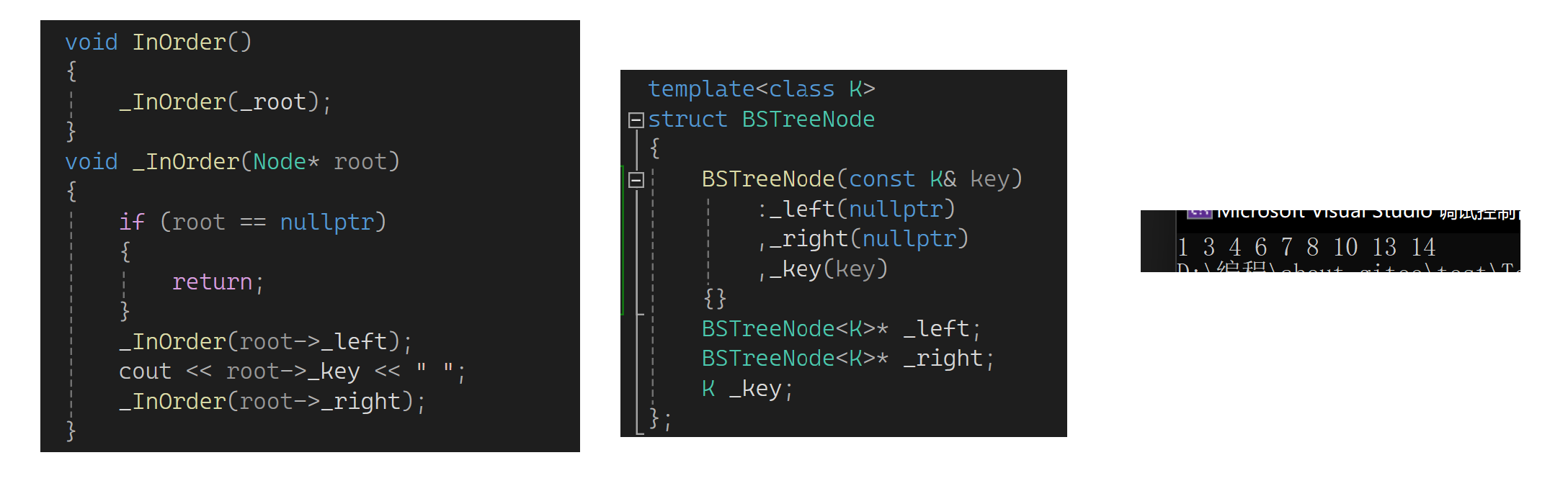
下面来写一下查找，比它大往右找，比它小往左走，找到了返回true，走到空还没有找到返回false：
这真正麻烦的是删除，比如这有一颗树：
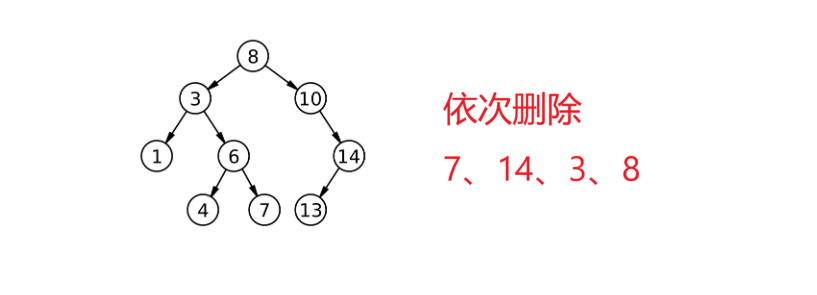
如果要删除7好不好删？可以通过规则找到7，找到后delete就行，然后把父亲指向7的改为指向空，因此叶子结点还是比较好删的：
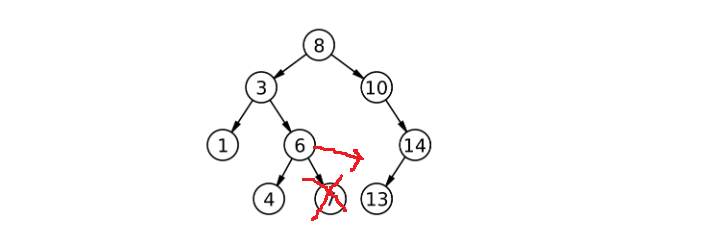
那14好删吗？也还可以，找到14把14delete了，然后父节点连14的子结点：
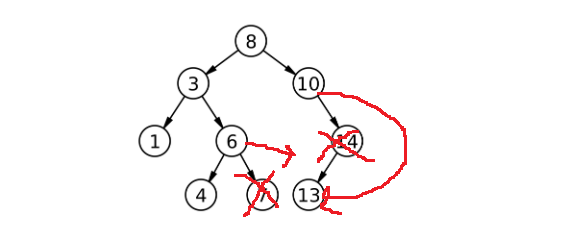
先总结一下上述：像7这样没孩子的删除最方便；像14这样的只有一个孩子，把孩子给14的父亲就行，14是10的右孩子，以14为根的树中所有的值都会比10大，让10的右指向14的一个孩子就行；没孩子和有一个孩子的情况都还好说。要删除3就麻烦了，这是两个孩子的情况怎么办？有一种方式是找个结点来替代要删除的结点，那谁可以替代？或者看要删除8，那谁可以替代8？替代后的要求是要仍然符合搜索二叉树，所以7和10是符合的。所以有两个孩子可以用替换法：找左子树的最大结点或右子树的最小结点，这样换下来符合搜索二叉树。左子树的最大结点是它的最右结点，右子树最小结点是它的最左结点。比如这里找7替换，先交换值，然后删了替换完的结点；替换完的结点一定是最右或最左结点，它最多只有一个孩子，肯定可以删：
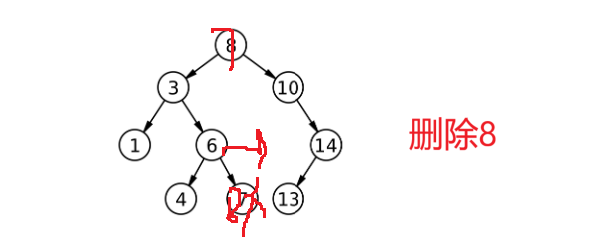
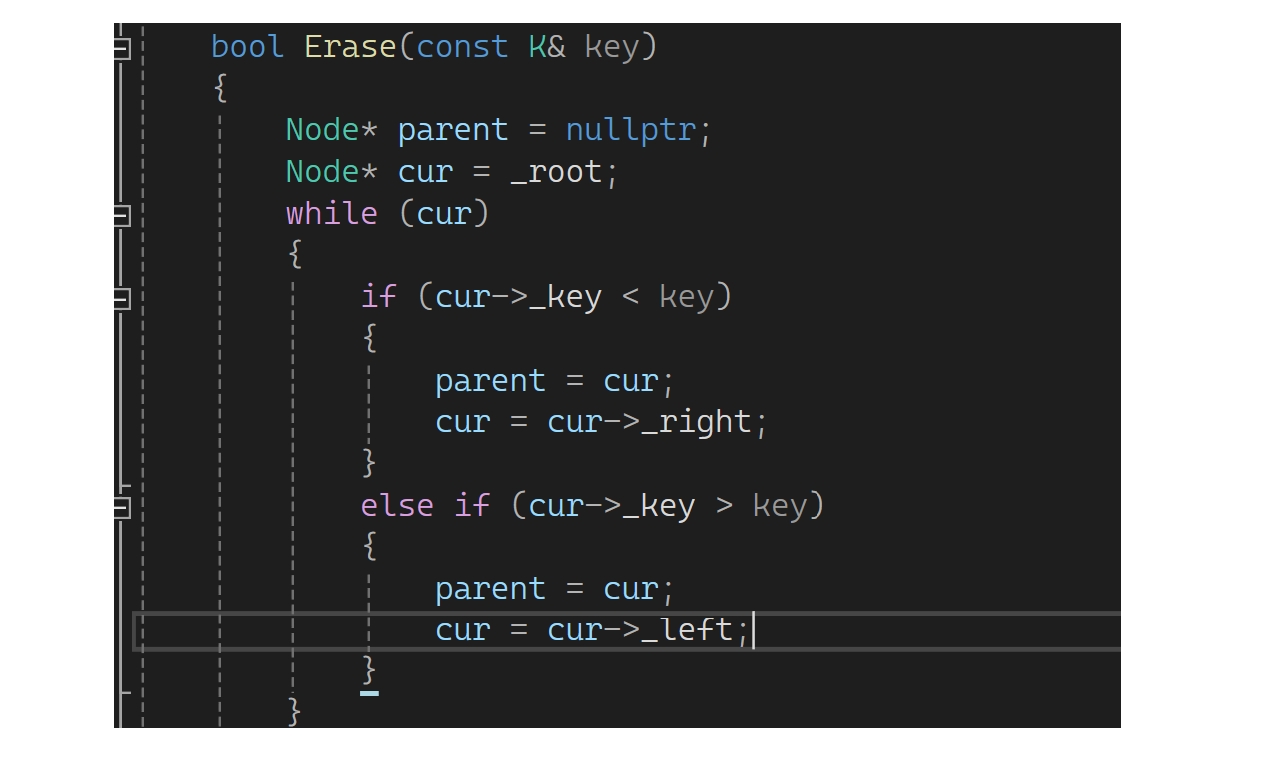
下面来实现：首先需要一个parent和cur(需要的parent的目的是找到后还要托孤)，大于往右找，同时更新parent；小于往左找，同时更新parent：
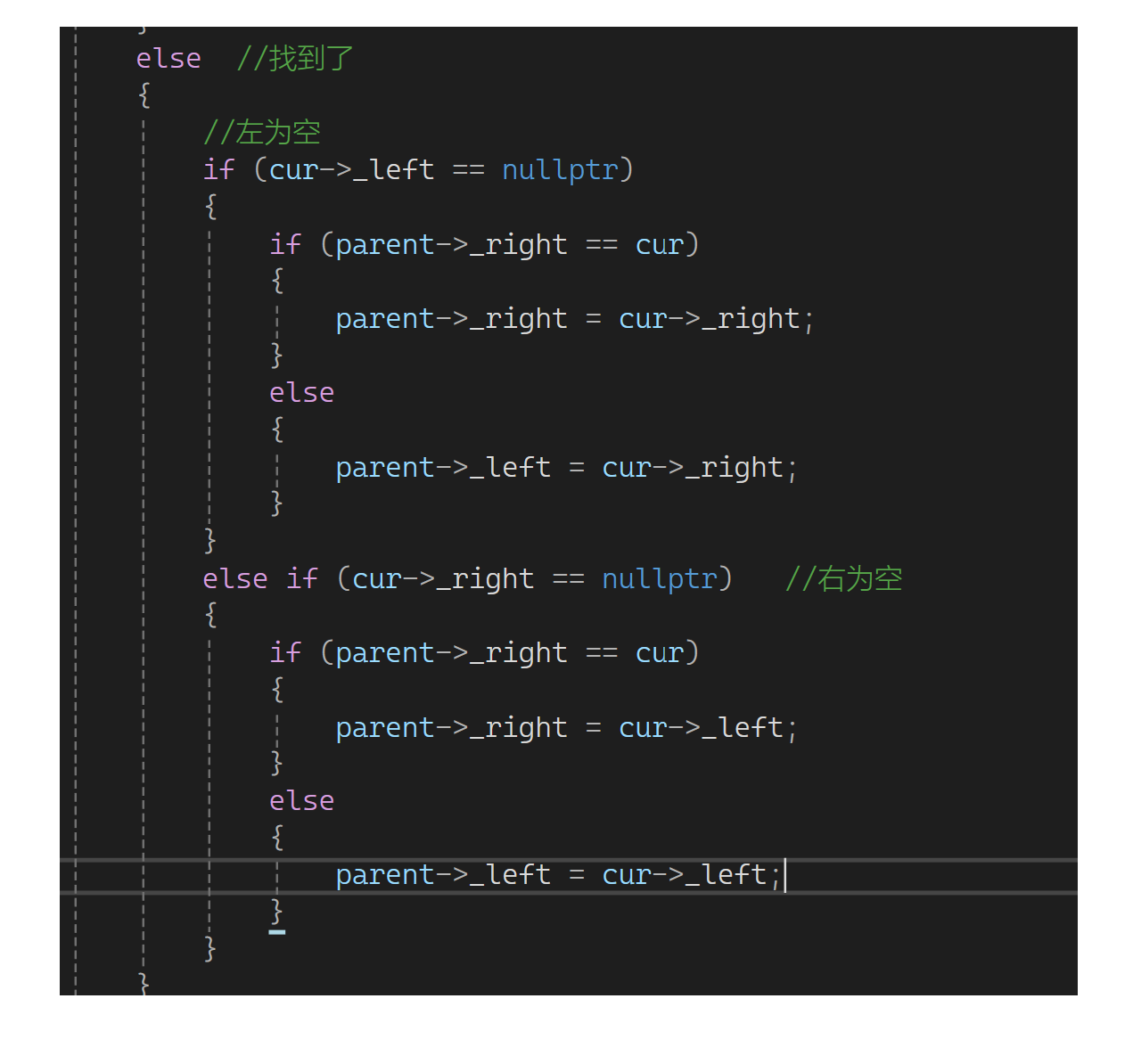
如果找到了，没孩子的和一个孩子的可以归为一类：左为空让父亲指向我的右，右为空让父亲指向我的左。那让父亲的什么指向我的左或右呢？假如是我左为空想让父亲指向我的右的情况：如果我是父亲的右，就让父亲的右指向我的右；如果我是父亲的左，就让父亲的左指向我的右。假如是我右为空让父亲指向我的左的情况：如果我是父亲的右，让父亲的右指向我的左；如果我是父亲的左，让父亲的左指向我的左：
但左为空和右为空这里还有个坑，如果cur是8就崩溃了，因为parent一直没有走是空：
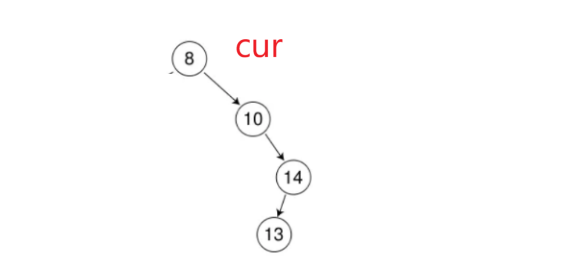
那这种情况如何处理？让根结点指向孩子位置就行：
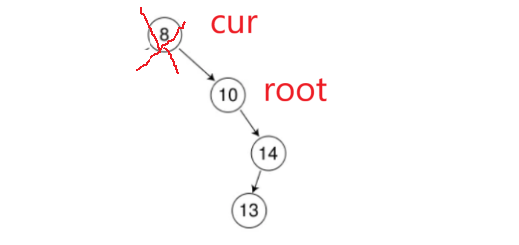
所以下面再补充一下：
现在处理左右都不为空的情况：先找替代结点，这里找左树的最大结点。我们先弄一个结点指针指向左树，然后一路向右走，找到最右结点完成交换(找最右结点的同时还要找到它的父亲，每次走之前更新父亲)：
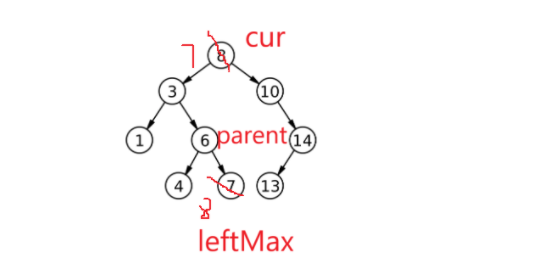
此时右为空，让父亲指向leftMax的左，但是父亲的谁指向我的左还要判断一下，因为还有一种极端情况：
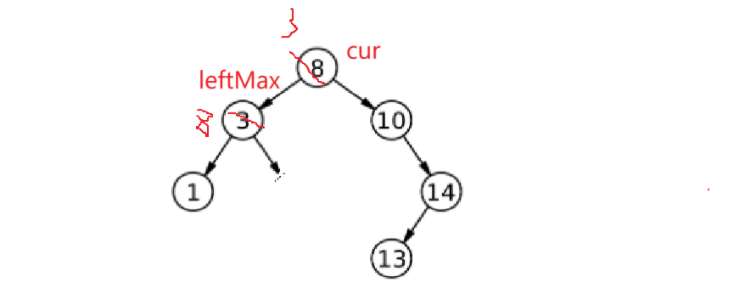
假如要删8，3是leftMax，这个是让父的左指向我的左。这里还有一个坑：leftMax并没有一直往右去找，所以parent一开始是空的。所以parent最开始给nullptr就坑了，最开始给cur，最后判断是parent的左指向我的左还是右指向我的左(因为我是最右，右肯定为空)。如果parent的左是leftMax，就让parent左指向leftMax的左；否则让parent的右指向leftMax的左。最后别忘了删除，把leftMax给cur，最后的地方删了：
下面测试一下：
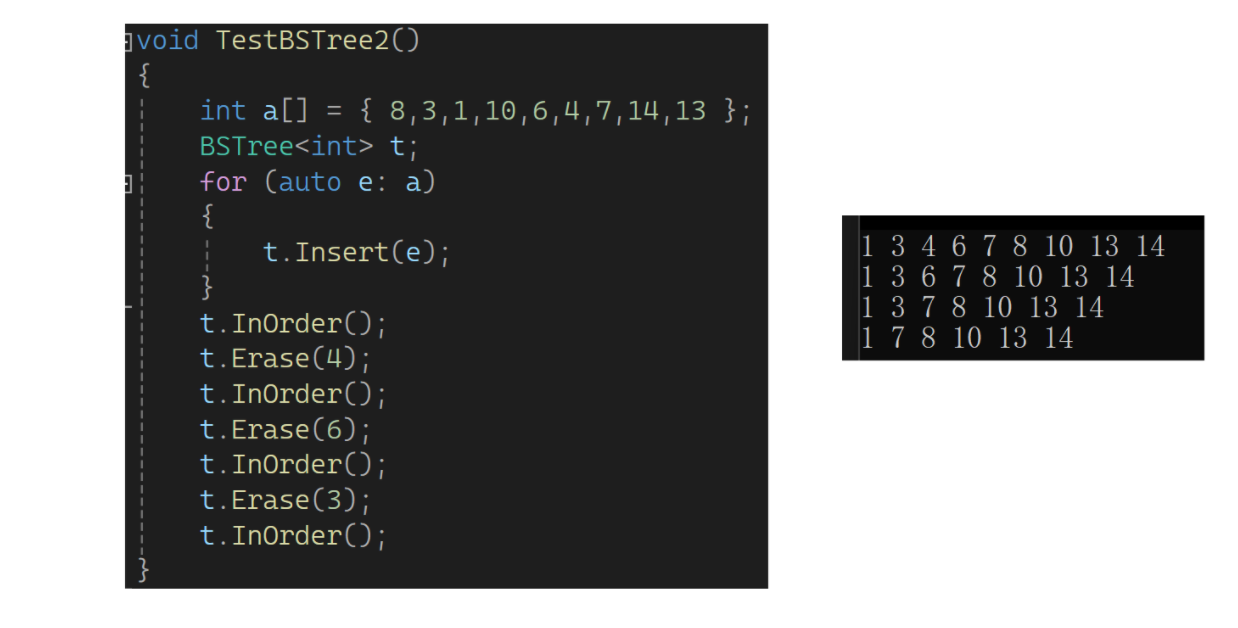
完整代码：
//.h
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode(const K& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //找到了
{
//左为空
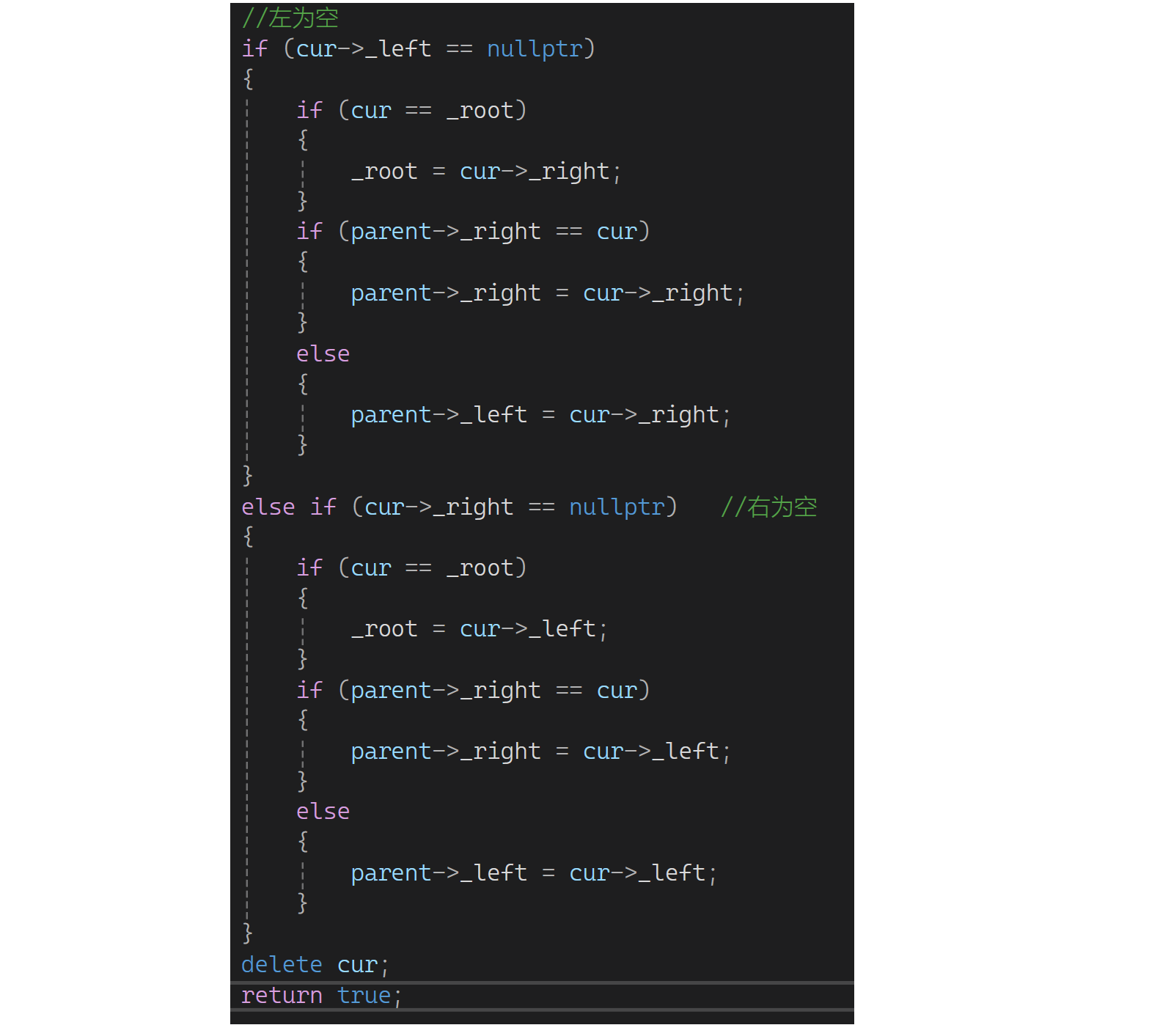
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
else if (cur->_right == nullptr) //右为空
{
if (cur == _root)
{
_root = cur->_left;
}
if (parent->_right == cur)
{
parent->_right = cur->_left;
}
else
{
parent->_left = cur->_left;
}
}
else
{
//找替代接结点
Node* parent = cur;
Node* leftMax = cur->_left;
while (leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
swap(cur->_key, leftMax->_key);
if (parent->_left == leftMax)
{
parent->_left = leftMax->_left;
}
else
{
parent->_right = leftMax->_left;
}
cur = leftMax;
}
delete cur;
return true;
}
}
}
private:
Node* _root;
};
void TestBSTree1()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
}
void TestBSTree2()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e: a)
{
t.Insert(e);
}
t.InOrder();
t.Erase(4);
t.InOrder();
t.Erase(6);
t.InOrder();
t.Erase(3);
t.InOrder();
}3.递归版本
下面来看看递归版本，首先说说Find，这里先插入一个小话题：C++里面凡是写递归都要单独写一个子函数：
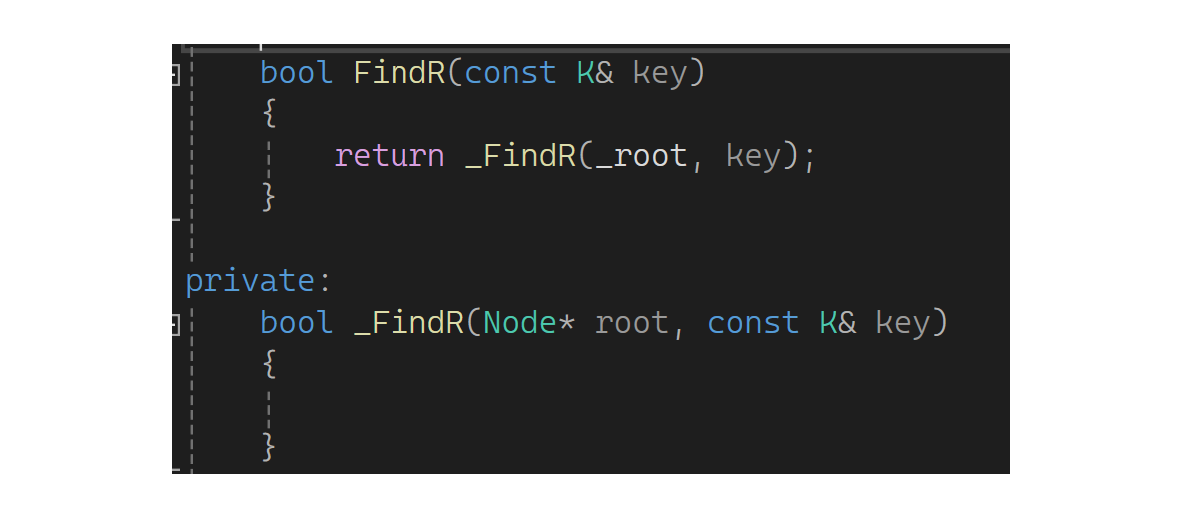
因为递归这里有参数的变化。那怎么写呢，以下图为例：
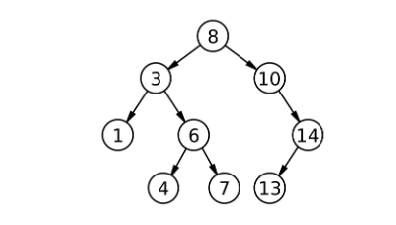
如果找的数一开始等于8就找到了，比8大转化到去右子树找，比8小转化到去左子树找。子树也是类似的过程，找到了层层返回，找不到也层层返回。下面来进行实现：如果root是空没找到返回false，如果比当前根大，到右子树去找；如果比当前根小，去左子树找；如果相等找到了返回true：
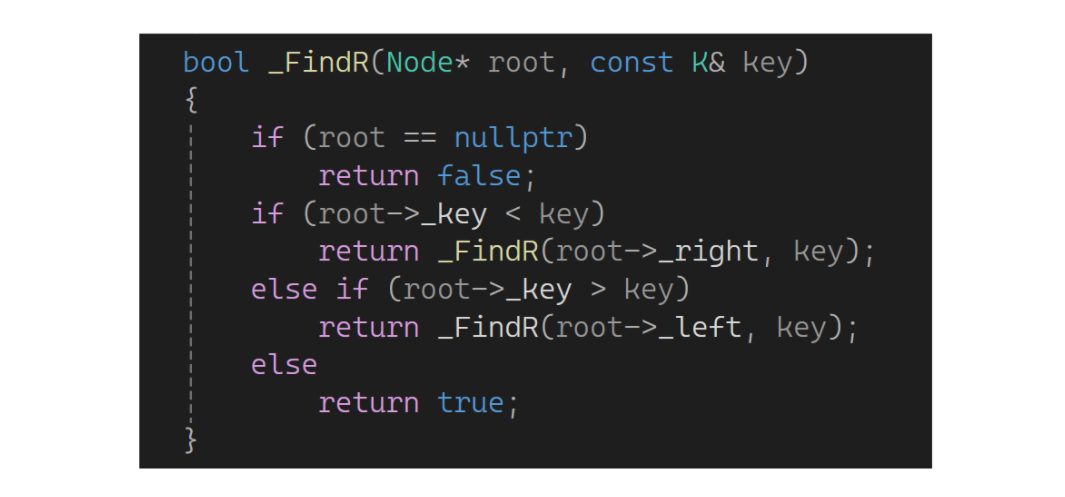
再来看插入，如果要插入的值比目前根所对应的小，就去左树插入；如果插入的值比当前根对应的大，就去右数插入；如果相等返回false；找到空就可以插入了：
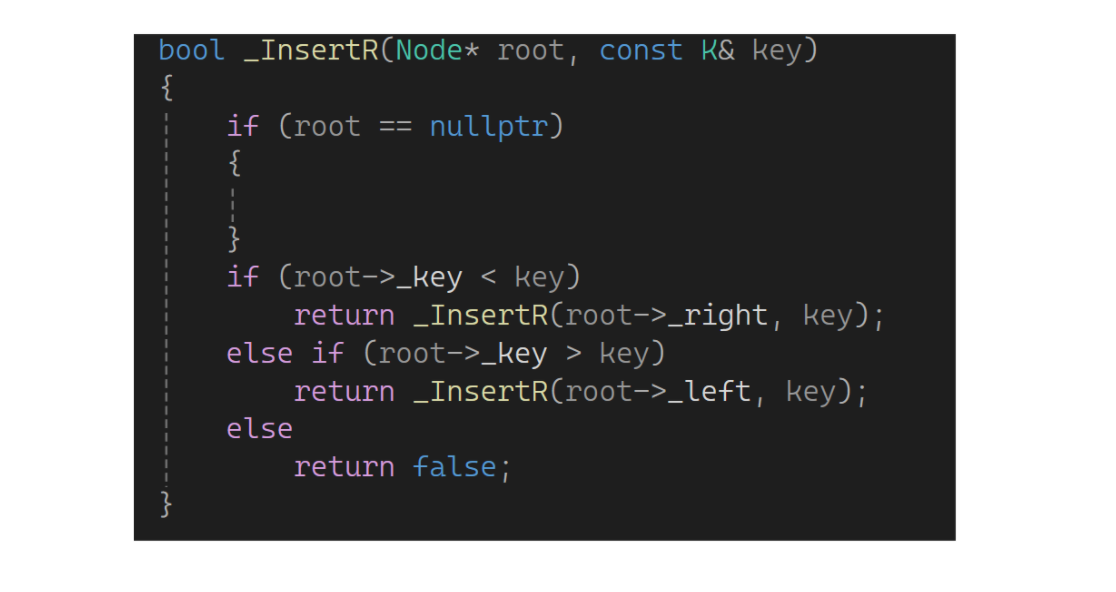
这里还是和以前一样面临找父亲的问题，可像以前一样添加paernt。但是还有个更简单的方式，加个引用：
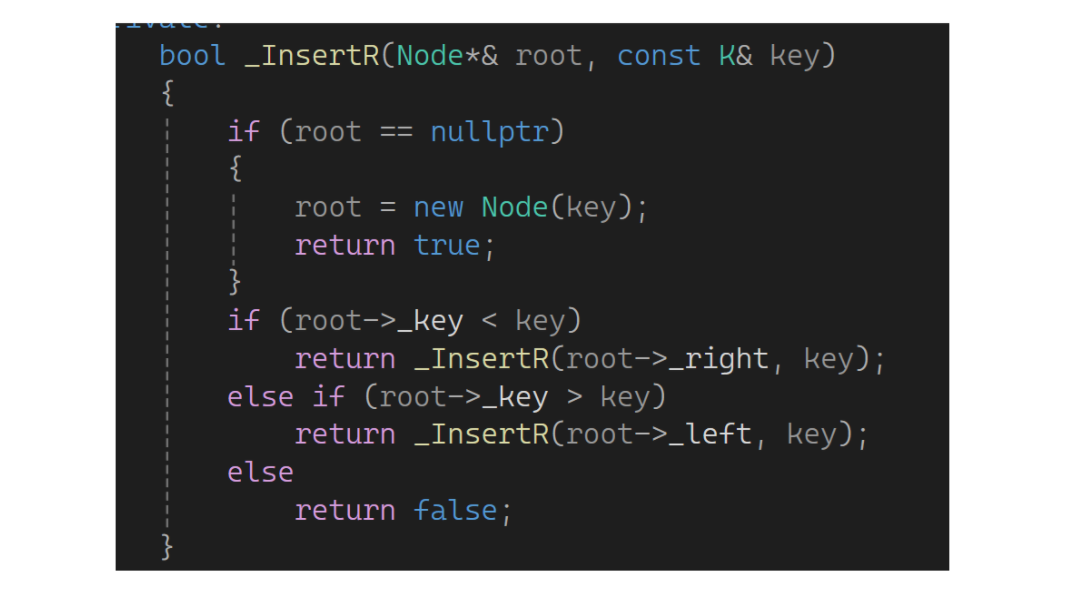
为啥要这样呢？
比如是空树，root是_root的别名，然后new一个结点就给_root了；比如结点到6了，，5比6小递归到6的左子树到4；5比4大，此时传4的右指针，root是4的右指针的别名，4的右指针是空，可以插入了；插入时new了一个结点直接给root，对root修改就是对4的右指针修改，所以这样就链接上了，不用找父亲和比较大小看连到父亲的谁了。
下面来实现删除，先弄好前置条件：如果root等于空返回false，说明找不到；如果要删的值比它大，转换成去右树删除；如果删的值比它小，转换成去左树删除；相等就要开始删这个值了：
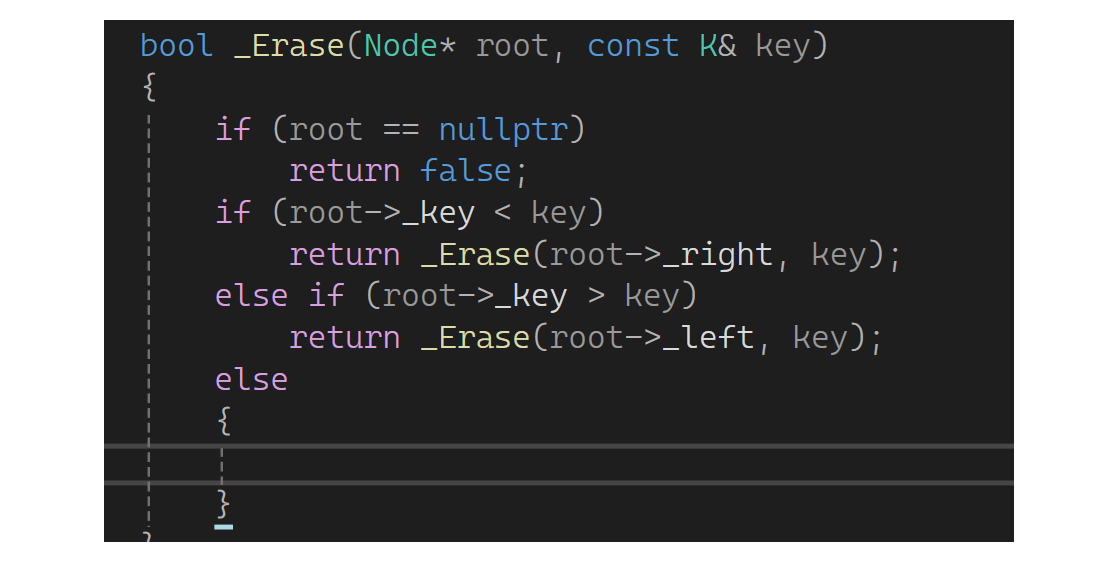
删除还是分三种情况：1.左为空 2.右为空 3.左右都不为空：
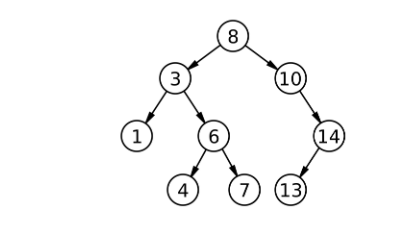
比如删14，比它大往右走，比它小往左走，找到后要删除：
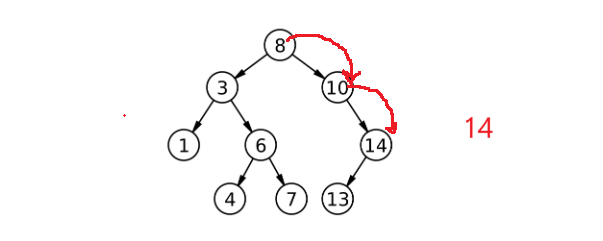
以前面对这些情况很繁琐：左为空让父亲指向右，右为空让父亲指向左，关键不知道让父亲的谁指向左和右；还有cur是root的情况。现在用引用是否会简化很多呢？左为空让父亲指向我的右，右为空让父亲指向我的左，剩下的都不管了(再此之前保存一下要删的结点，防止丢了没法删)：
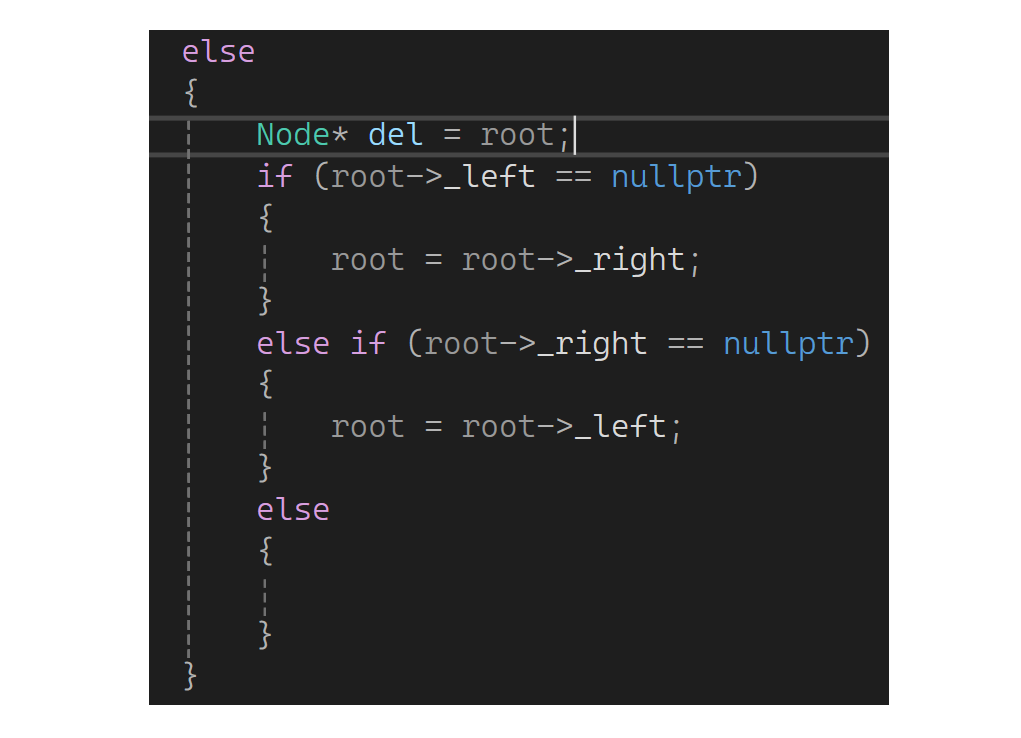
现在来体会：假设已经走到10了，删14；14比10大，再往下递归时，下一层的root是10的右指针14的别名；现在找到了，14是一个右为空，root的值是10的右指针，再取left是13，给root相当于10的右指针指向了13：
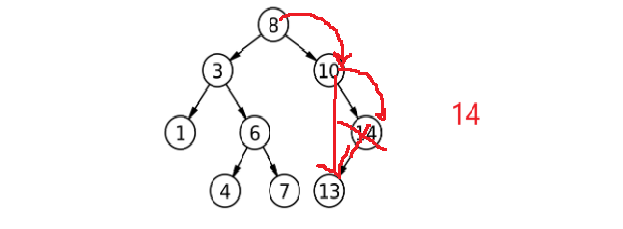
对于删8的这种情况：
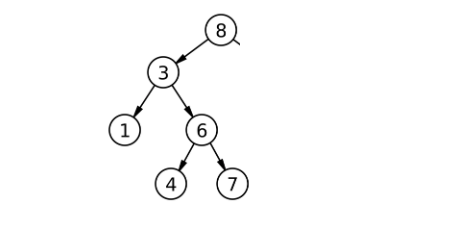
root是_root的别名，右为空，直接root = root->left。下面再来看左右都不为空的问题：
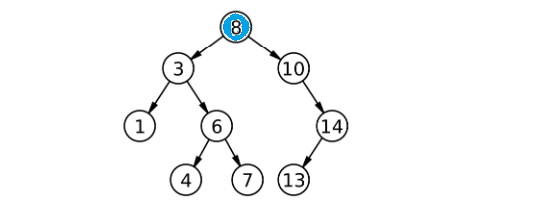
假设要删除的是8，用左树最大结点或右数最小结点替换：
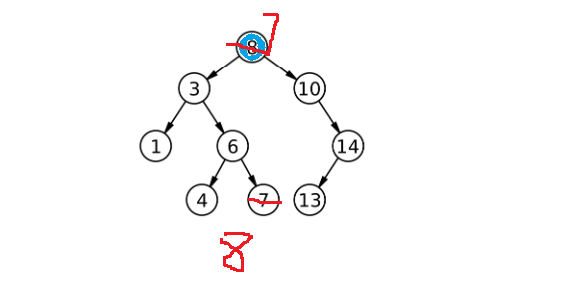
现在不能递归去删，因为结构变了，8比7大往右找，找不到8。在原有树删不行，可转化为去左树递归删除。下面来实现：找到要替换的结点，交换，转化为递归去左子树中删key：
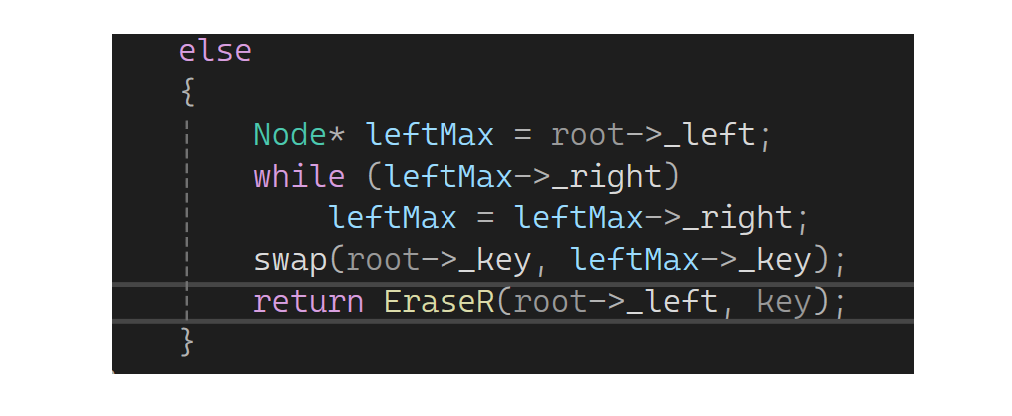
若成功删除了释放结点返回true：
bool _Erase(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
return _Erase(root->_right, key);
else if (root->_key > key)
return _Erase(root->_left, key);
else
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* leftMax = root->_left;
while (leftMax->_right)
leftMax = leftMax->_right;
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}下面来测试一下：
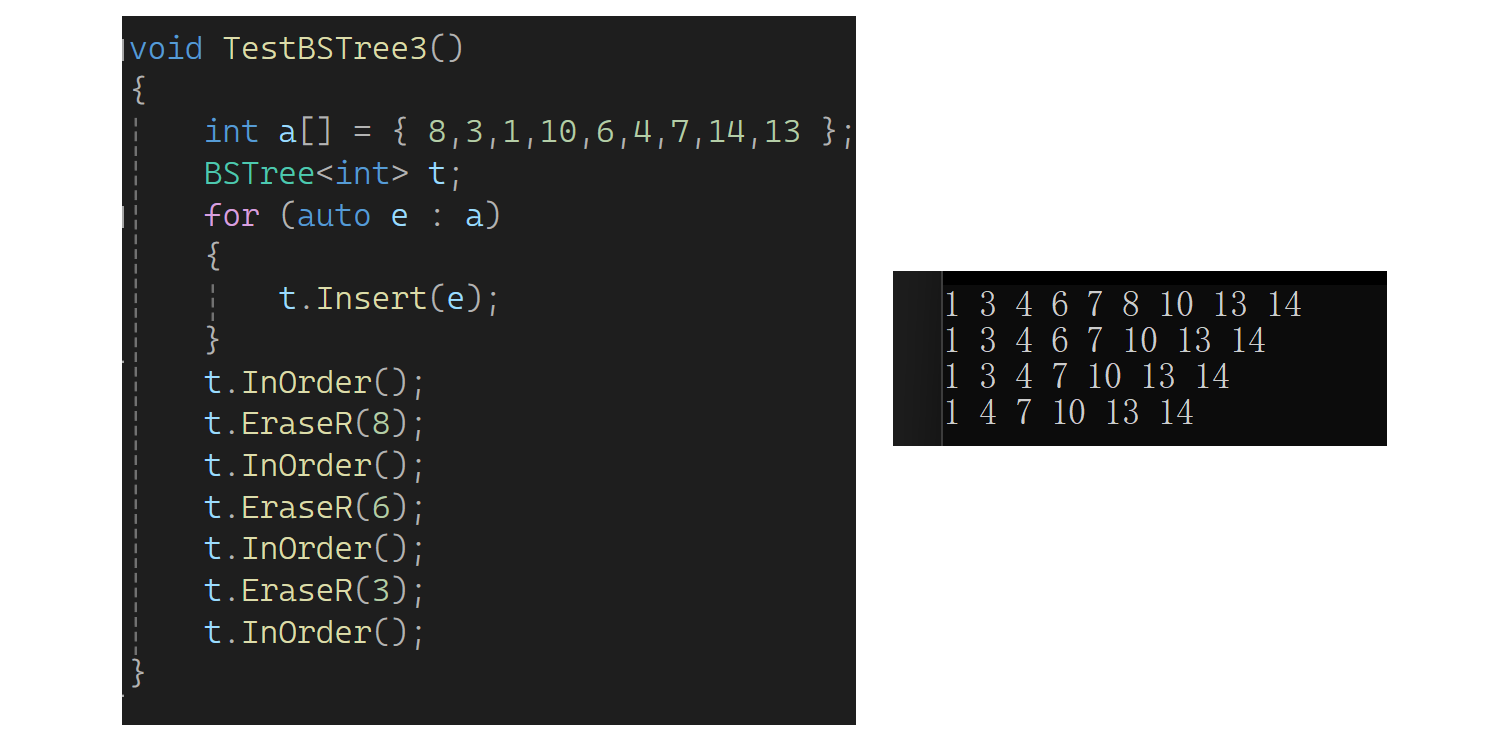
下面来完善一下，首先写一下析构，也需要子函数走递归。可以走个后续删除，加个引用，完成内部置空：
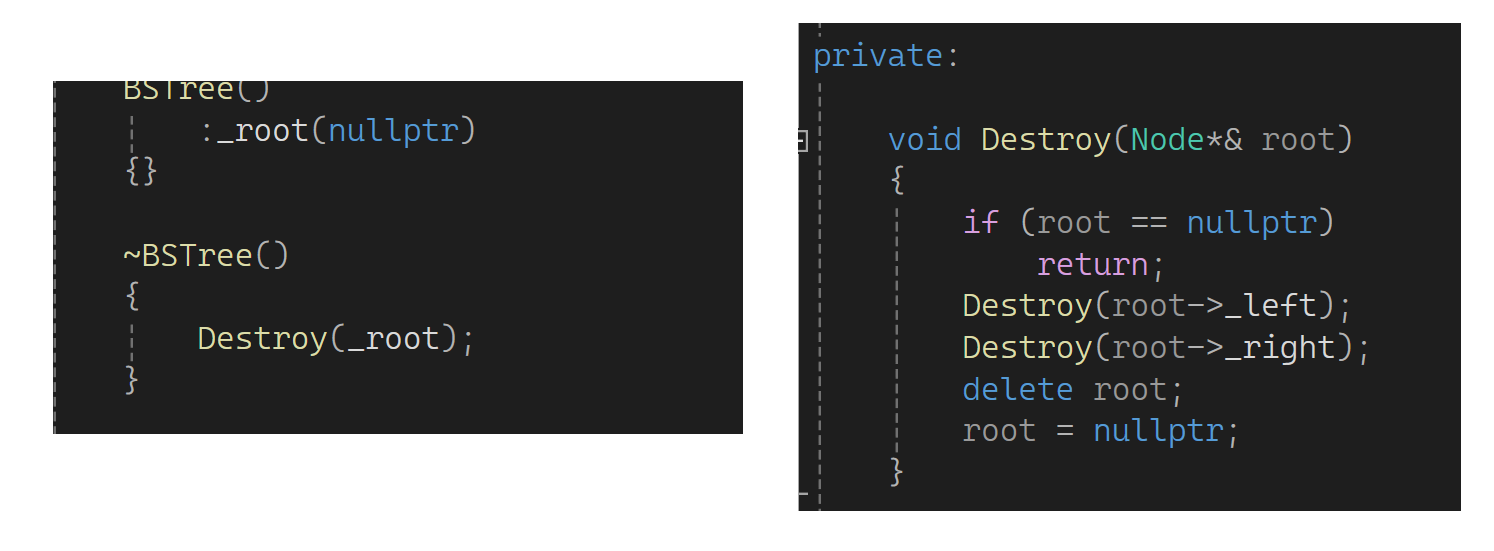
再来写个拷贝构造，有人会说拷贝可以由中序不断调insert来实现：
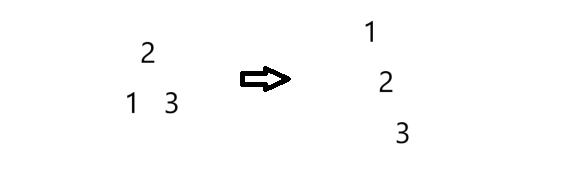
这样不能保证顺序。若直接这样：
上面是一个浅拷贝，会引发两次析构就崩溃了，所以要写一个深拷贝。这里需要写一个Copy函数，通过Copy来拷贝这个树，拷贝好后赋值给_root：
那Copy怎么写呢？
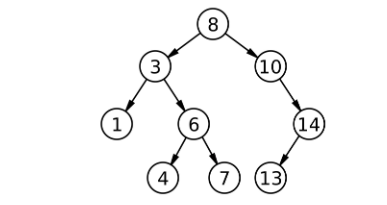
可以前序递归走，先遍历8就copy一个8出来；遇到3就copy一个3出来；遇到1就copy一个1出来；遇到空1左边链接一个空；遇到空1右边再链接一个空，弄完1就回去...下面来实现：遇到空就返回一个空，不是空就new一个结点出来；拷贝结点左边连左边拷贝好的，右边连右边拷贝好的，最后返回拷贝结点：
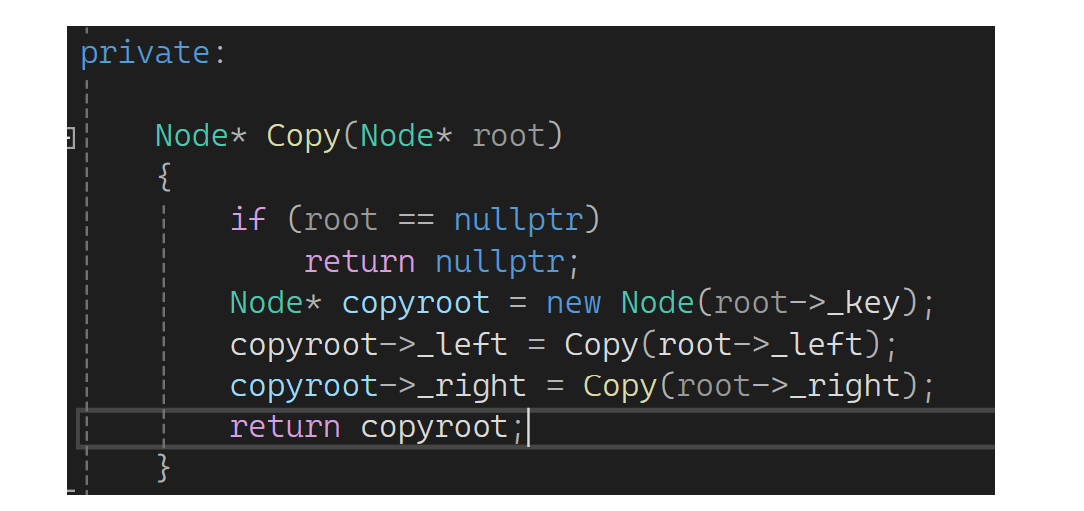
最后再来写一下赋值，这里用现代写法，直接传值然一交换：
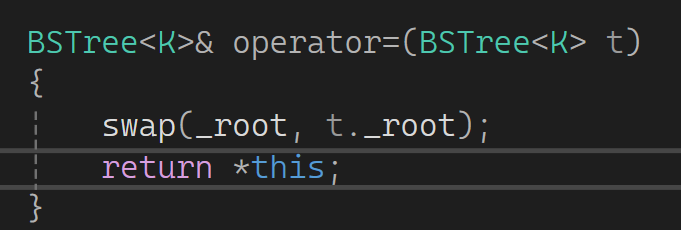
完整代码：
#pragma once
template<class K>
struct BSTreeNode
{
BSTreeNode(const K& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
~BSTree()
{
Destroy(_root);
}
BSTree(const BSTree<K>& t)
{
_root = Copy(t._root);
}
BSTree<K>& operator=(BSTree<K> t)
{
swap(_root, t._root);
return *this;
}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //找到了
{
//左为空
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
if (parent->_right == cur)
{
parent->_right = cur->_right;
}
else
{
parent->_left = cur->_right;
}
}
else if (cur->_right == nullptr) //右为空
{
if (cur == _root)
{
_root = cur->_left;
}
if (parent->_right == cur)
{
parent->_right = cur->_left;
}
else
{
parent->_left = cur->_left;
}
}
else
{
//找替代接结点
Node* parent = cur;
Node* leftMax = cur->_left;
while (leftMax->_right)
{
parent = leftMax;
leftMax = leftMax->_right;
}
swap(cur->_key, leftMax->_key);
if (parent->_left == leftMax)
{
parent->_left = leftMax->_left;
}
else
{
parent->_right = leftMax->_left;
}
cur = leftMax;
}
delete cur;
return true;
}
}
}
bool FindR(const K& key)
{
return _FindR(_root, key);
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
Node* Copy(Node* root)
{
if (root == nullptr)
return nullptr;
Node* copyroot = new Node(root->_key);
copyroot->_left = Copy(root->_left);
copyroot->_right = Copy(root->_right);
return copyroot;
}
void Destroy(Node*& root)
{
if (root == nullptr)
return;
Destroy(root->_left);
Destroy(root->_right);
delete root;
root = nullptr;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
return _EraseR(root->_right, key);
else if (root->_key > key)
return _EraseR(root->_left, key);
else
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* leftMax = root->_left;
while (leftMax->_right)
leftMax = leftMax->_right;
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}
bool _FindR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
return _FindR(root->_right, key);
else if (root->_key > key)
return _FindR(root->_left, key);
else
return true;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root;
};
void TestBSTree1()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e : a)
{
t.Insert(e);
}
t.InOrder();
}
void TestBSTree2()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e: a)
{
t.Insert(e);
}
t.InOrder();
t.Erase(4);
t.InOrder();
t.Erase(6);
t.InOrder();
t.Erase(3);
t.InOrder();
}
void TestBSTree3()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e : a)
{
t.InsertR(e);
}
t.InOrder();
t.EraseR(8);
t.InOrder();
t.EraseR(6);
t.InOrder();
t.EraseR(3);
t.InOrder();
}
void TestBSTree4()
{
int a[] = { 8,3,1,10,6,4,7,14,13 };
BSTree<int> t;
for (auto e : a)
{
t.InsertR(e);
}
BSTree<int> t1(t);
t.InOrder();
t1.InOrder();
}4.搜索二叉树的应用
下面来说说搜索二叉树的应用，它的应用场景有两个：第一个叫key的搜索模型，第二个叫key/value的搜索模型。key的搜索模型是日常快速判断在不在的场景，比如门禁系统，小区车辆出入系统等；再比如key模型可以检查一个英文文章单词是否拼写正确，通过读取词库放到一颗搜索树，读取单词看在不在树里，不在就拼写错误。key/value模型是日常通过一个值找另一个值，比如通过手机号查快递信息，商场通过车牌算停车时间来收费。那搜索二叉树怎样完成这样的场景呢？(key的就不说了，前面的实现其实就是key的)下面来看一下key/value的模型，用搜索二叉树如何做key/value模型？key/value就是通过key来找value，所以结点里面存两个值：
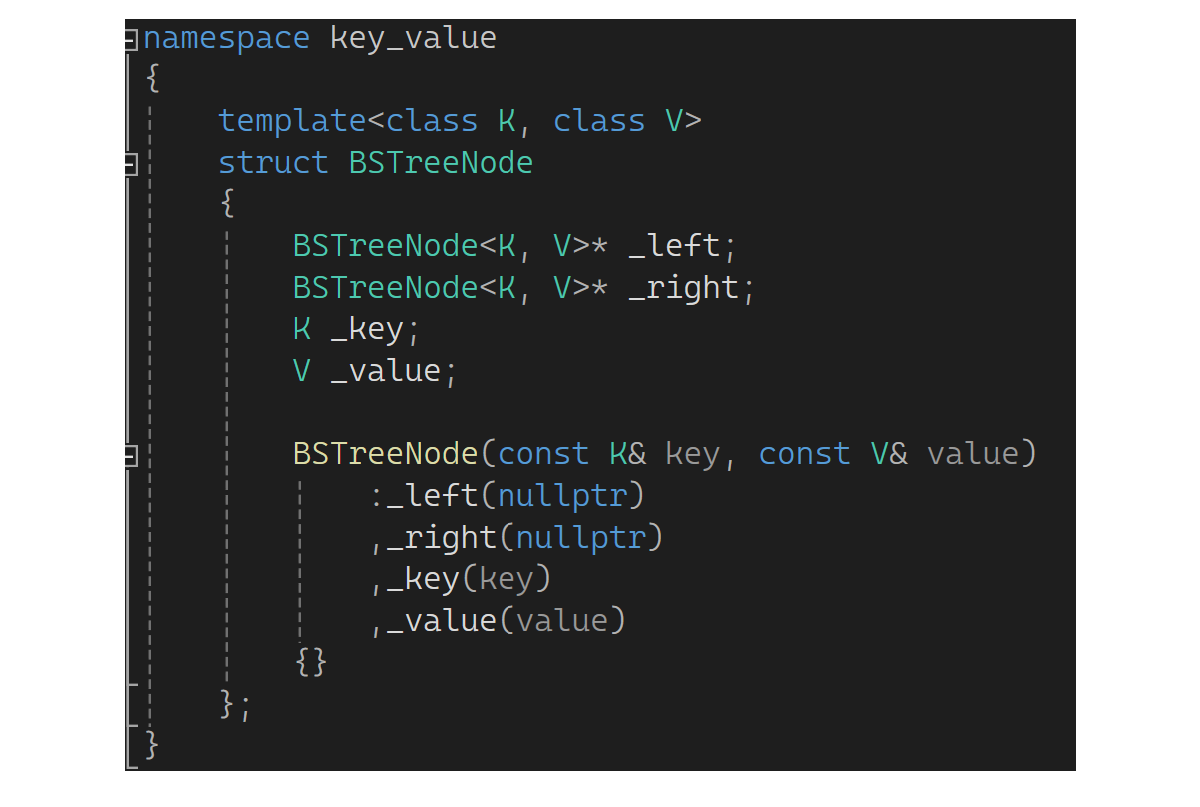
插入的时候除了key还有val，所以模板参数变为两个：
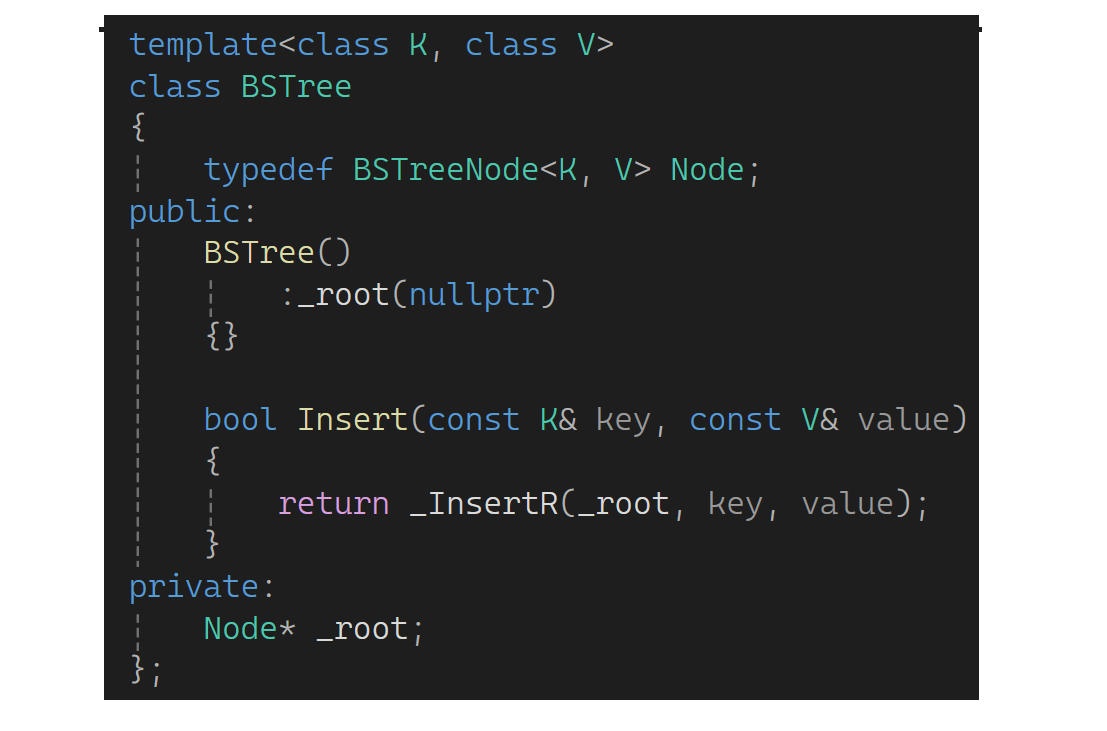
插入时比它大往右边走，比它小往左走，value不参与比较过程，还是依赖key走，value仅是为了找到存key位置存的时候把val也存进去：
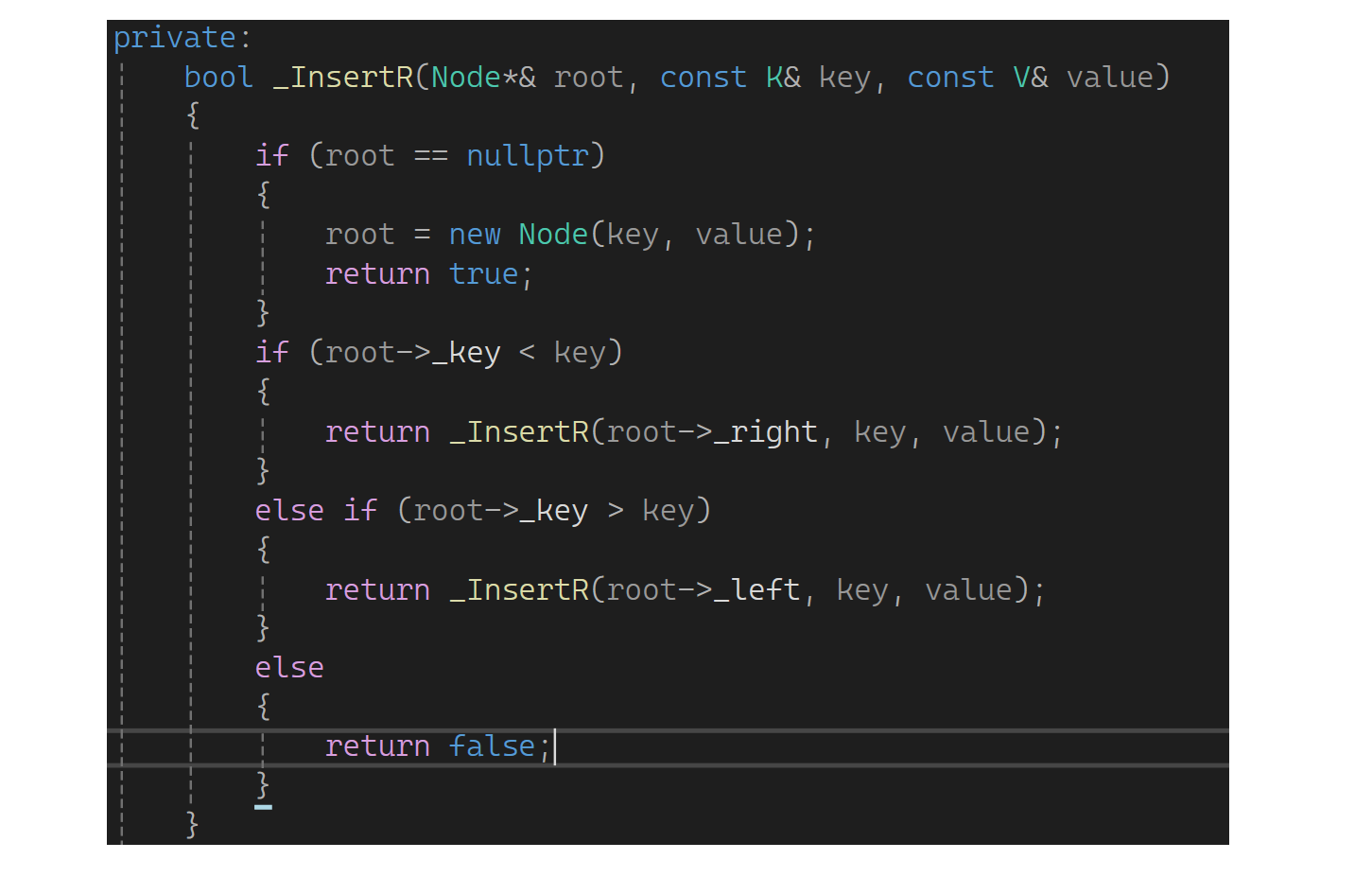
查找的时候比它大往右走，比它小往左走，搜索树的key是不可以修改的，因为如果修改了可能就不是搜索树了，但可以改val。所以find变一下，这里返回结点的指针，因为有结点指针就能弄很多东西，比如修改value：
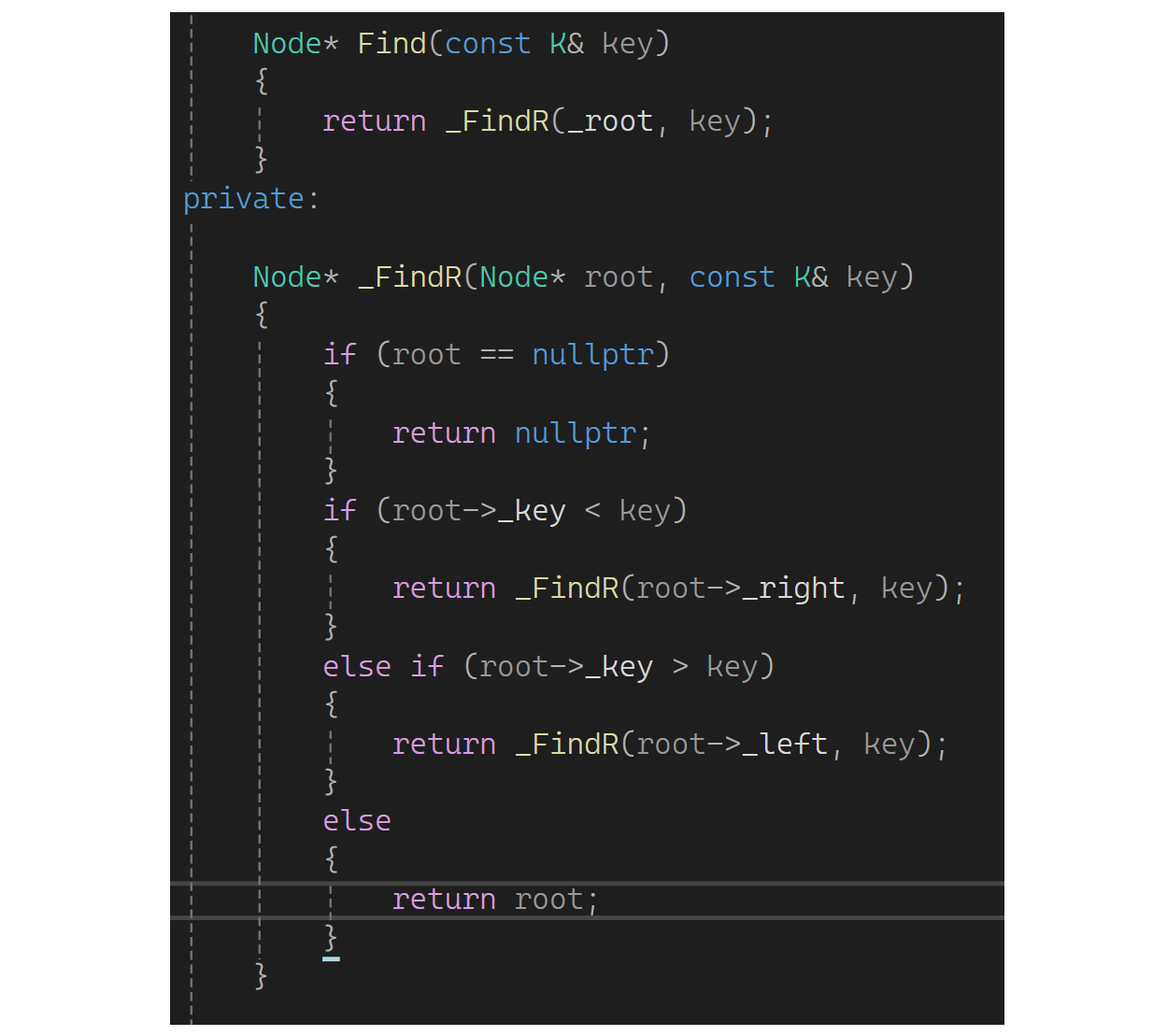
删除的时候要不要给value？不用给，但要删，因为主要以key为主，val是顺便的事：
namespace key_value
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value)
:_left(nullptr)
,_right(nullptr)
,_key(key)
,_value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool Insert(const K& key, const V& value)
{
return _InsertR(_root, key, value);
}
Node* Find(const K& key)
{
return _FindR(_root, key);
}
void Erase(const K& key)
{
_EraseR(_root, key);
}
private:
void _InOrder(Node* root)
{
if (root == NULL)
{
return;
}
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
bool _EraseR(Node* root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else
{
Node* del = root;
if (root->_left == nullptr)
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
Node* leftMax = root->_left;
while (leftMax->_right)
{
leftMax = leftMax->_right;
}
swap(root->_key, leftMax->_key);
return _EraseR(root->_left, key);
}
delete del;
return true;
}
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return root;
}
}
bool _InsertR(Node*& root, const K& key, const V& value)
{
if (root == nullptr)
{
root = new Node(key, value);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key, value);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key, value);
}
else
{
return false;
}
}
Node* _root;
};
}这里举一个中英互译的字典：
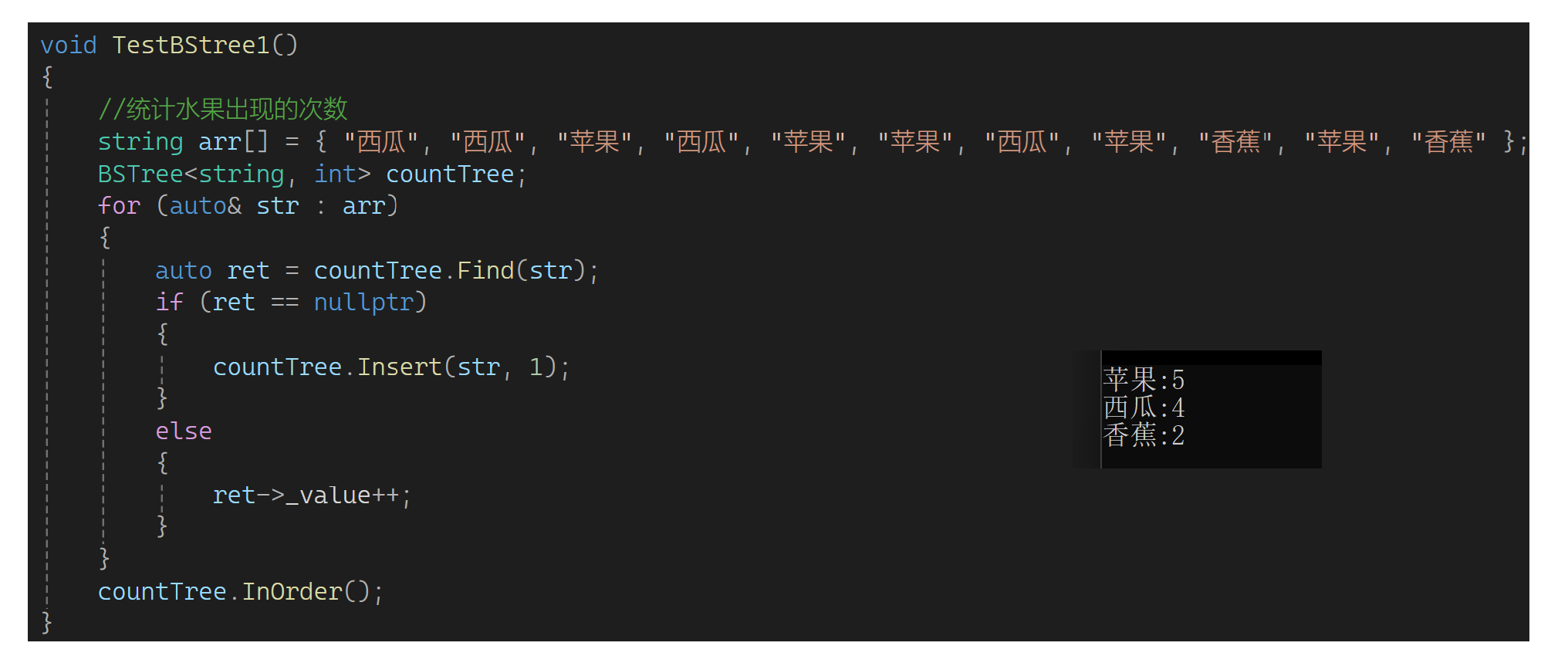
再看另一个场景，有一堆水果，想统计水果出现的次数怎么统计？
可以定义一颗树，树的king是string，val是int。遍历这里的水果，如果水果在树里面没有出现就插入，说明这个水果是第一次出现，此时key是水果，val是1。如果这个说过已经在树里面了，就让次数去++：
5.二叉树进阶题目
这道题要根据二叉树创建字符串，要求每一颗树里面左右子树用括号括起来，如：
(左图)先是根1，1完了后1的左子树要括起来，左子树根是2，2完了后再括2的左右子树；然后括1的右子树。其它空括号可以省略，但是如果左为空右不为空就不能省略，否则无法区分。题目要求是个前序遍历，只是左右子树用括号扩一下。下面来实现：如果root是空就返回空，不是空把这棵树前序遍历：根，左子树，在遍历左子树前给左括号，左子树完了给右括号；右数带括号是一样的逻辑：
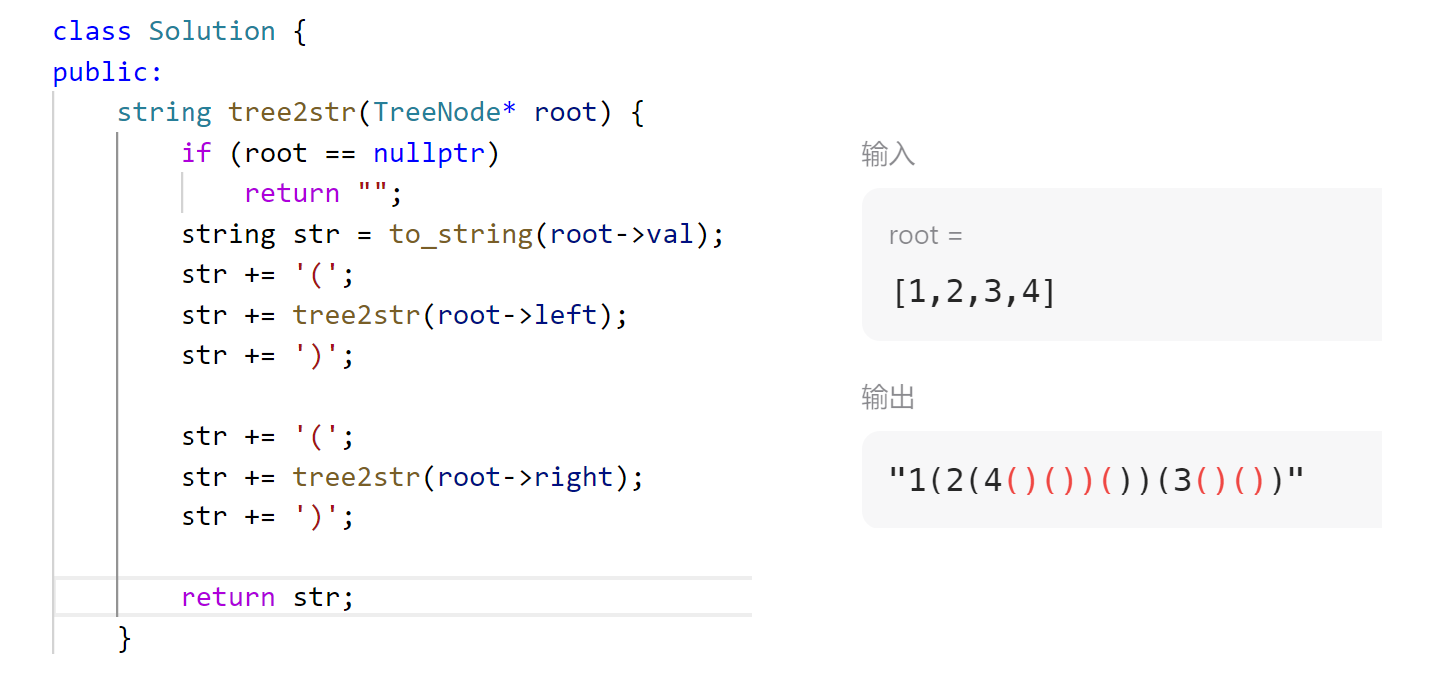
现在如果左为空，右为空，左右括号不保留；左不为空左括号保留，右为空也不需要保留右括号：
236. 二叉树的最近公共祖先 - 力扣（LeetCode）
https://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/description/沿着路径往根走的都可以认为它是祖先，如图：
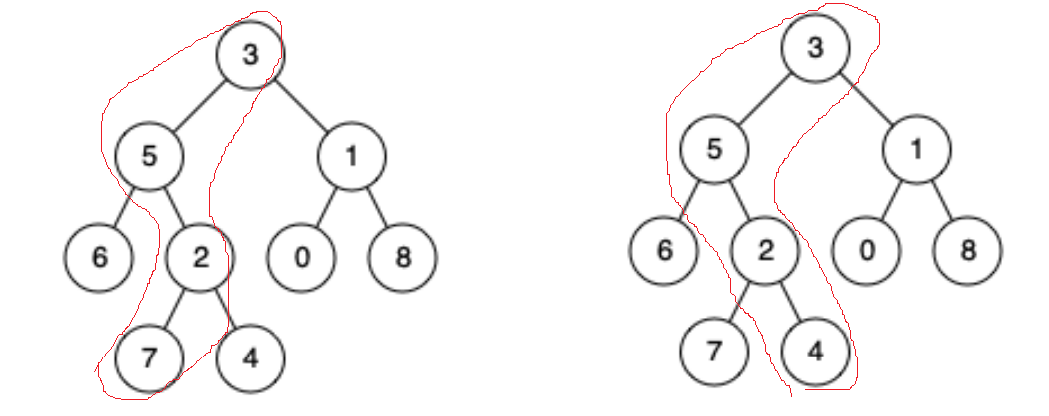
2，5，3是4和7的共有祖先，2是4和7的最近祖先。假如这个树是个三叉树(left，right，parent)，可转化为链表相交问题去找祖先。那普通树怎么找？可观察一下这些情况：
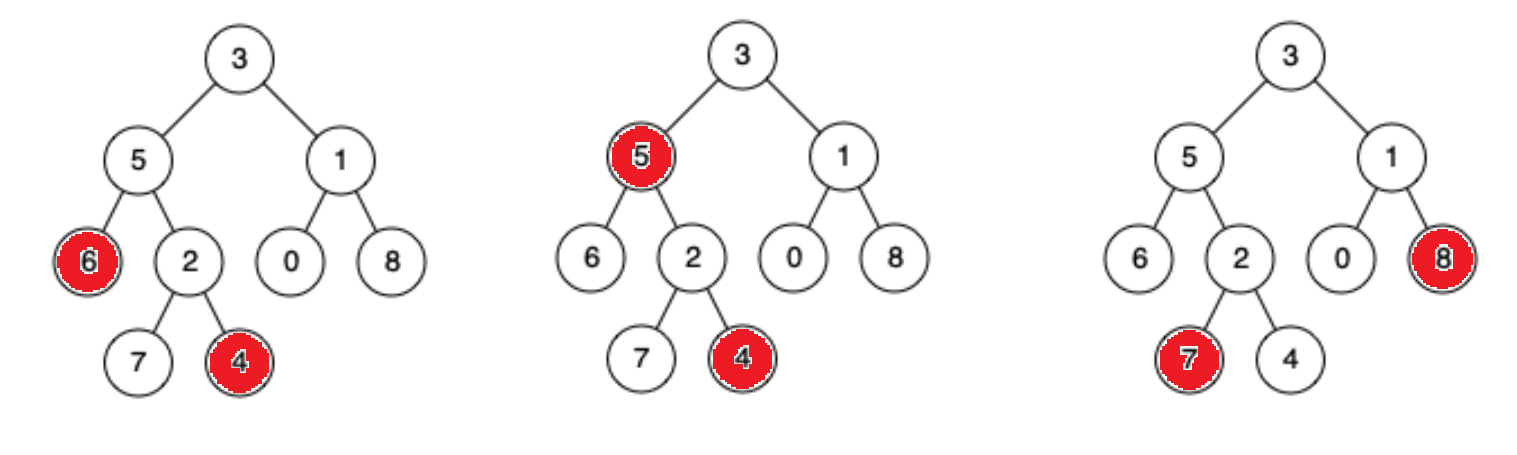
从第一个根开始看，一个在我的左子树，一个在我的右子树，那么当前根就是公共祖先；要是都在当前根的左树或右树就递归进去找看在不在递归树的左右。下面实现：如果root是空返回空，如果root是p或q就返回root。(还需要写个查找结点查在这棵树中有没有x结点，有返回true，没有返回false)定义pInleft，pInright，qInleft，qInright；先去左树查p，左边没找到就在右边，再去确认q以同样的方式。如果pq都在左边递归去左子树找，都在右边递归到右子树找；若在两边直接返回root公共祖先：
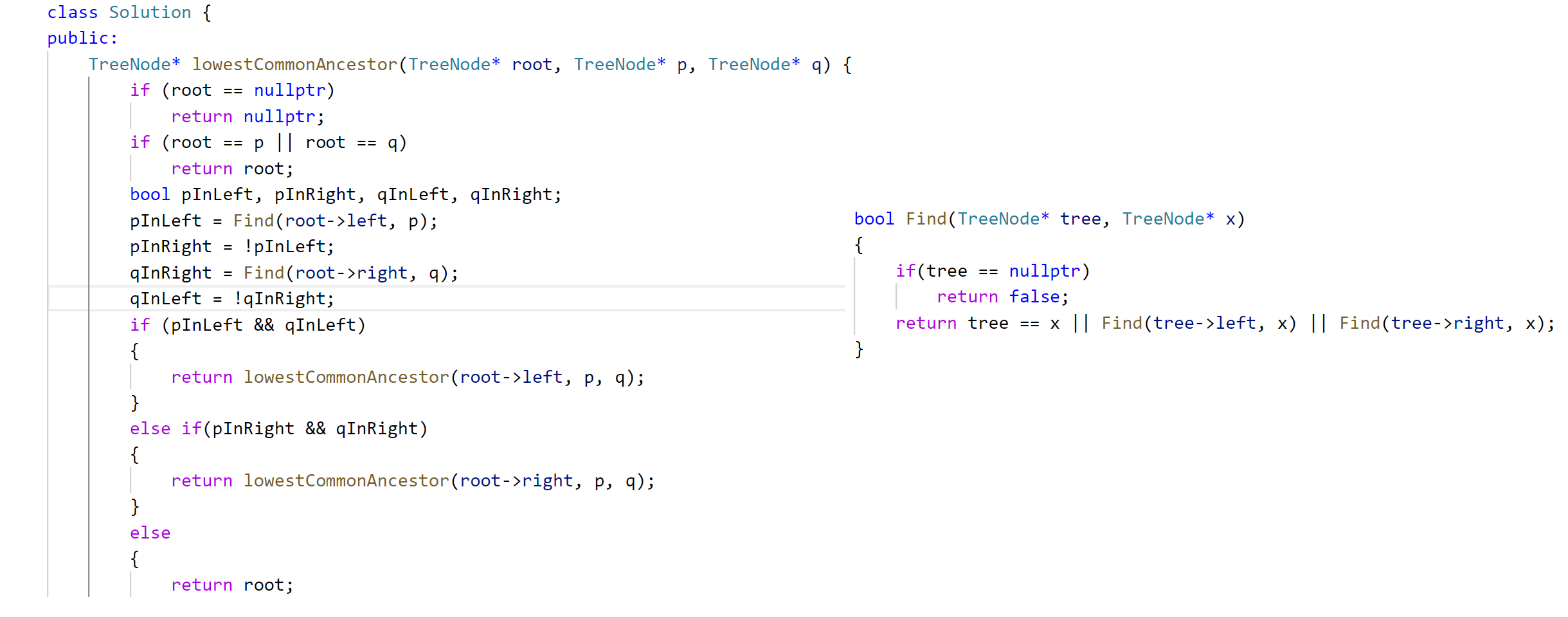
继续说公共祖先的问题，前面的解法时间复杂度是O(N^2)，如何优化到O(N)呢？如果不是普通树可以倒着走，类似于链表相交问题。但这里是普通树，可以想想理路径的方法，可以借助栈来求路径，如图：
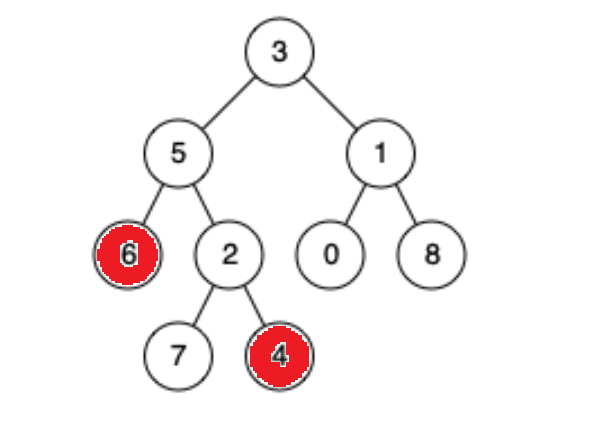
假设求6和4的路径怎么求？借助栈，前序走，不是要找的结点就直接入栈(先入栈，再判断是不是)，先来找6：3入栈，判断不是；5入栈，判断不是；6入栈，判断是，然后一路返回true。再来找4：3入栈，判断不是；5入栈，判断不是；6入栈判断不是；6左边没有返回false，6右边没有返回false，现在6的左右都没有，自己也不是要找的结点，6不可能是结点我们要找的结点中路径的一个，返回false同时把6pop掉。此时5的左边没有找到去右边找，2入栈，判断不是；7入栈，判断不是；7的左边没有返回false，7的右边没有返回false，7不可能是要找的结点返回false的同时pop一下。再去2的右边找，4是要找的结点，一路返回true：
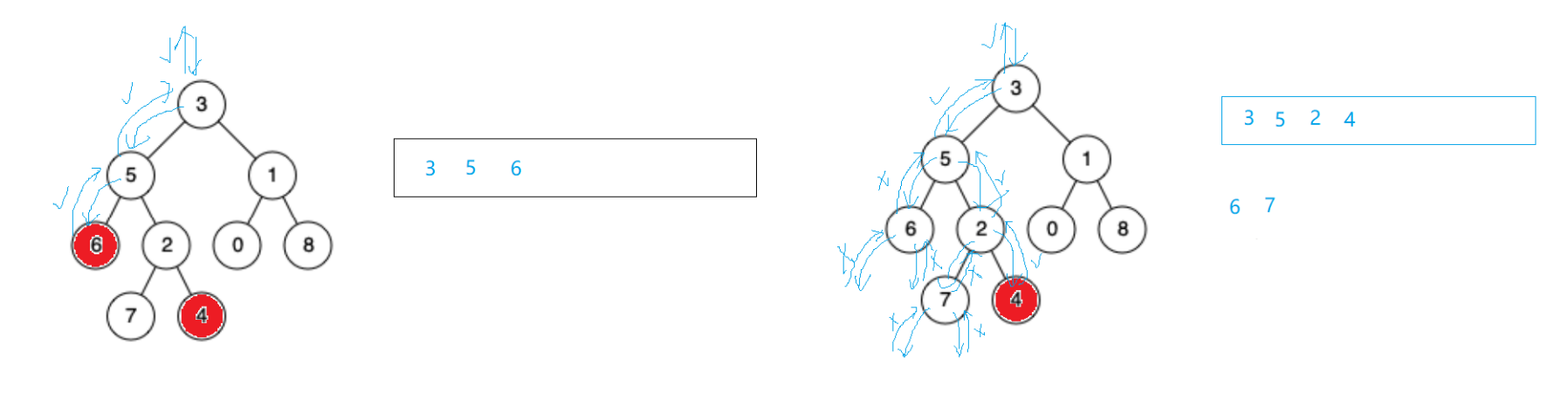
找节点过程把路径中的结点放到了一个栈里面，此时两个栈的size不相等，让大的那个pop，然后相等后比较，第一个相等的就是公共祖先O(N)。下面来实现：首先要找结点，如果root是空，返回false；若不是空，先把结点入进去，如果root==x，说明找到了返回true；若当前结点不是就递归到左边找，找到了就不去右边找，返回true；如果左边没找到递归右边找，找到了返回true；若当前结点左右都不是，pop一下，返回false给上一层。题目中说了p和q一定在，定义两个栈分别查找存，找完路径让长的先走；如果ppath大让它pop，qpath大让它pop；一样大后不相等pop，相等就是公共祖先：
二叉搜索树与双向链表_牛客题霸_牛客网 (nowcoder.com)https://www.nowcoder.com/practice/947f6eb80d944a84850b0538bf0ec3a5?tpId=13&&tqId=11179&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking题目要求把二叉搜索树变成有序双向链表；这道题如果没有没有其它要求可以放一个vector，中序遍历把二叉树的结点存起来，然后把前后结点都链接起来。但题目限制了条件，不能新建一个结点，要在原树上操作。那这道题怎么处理：
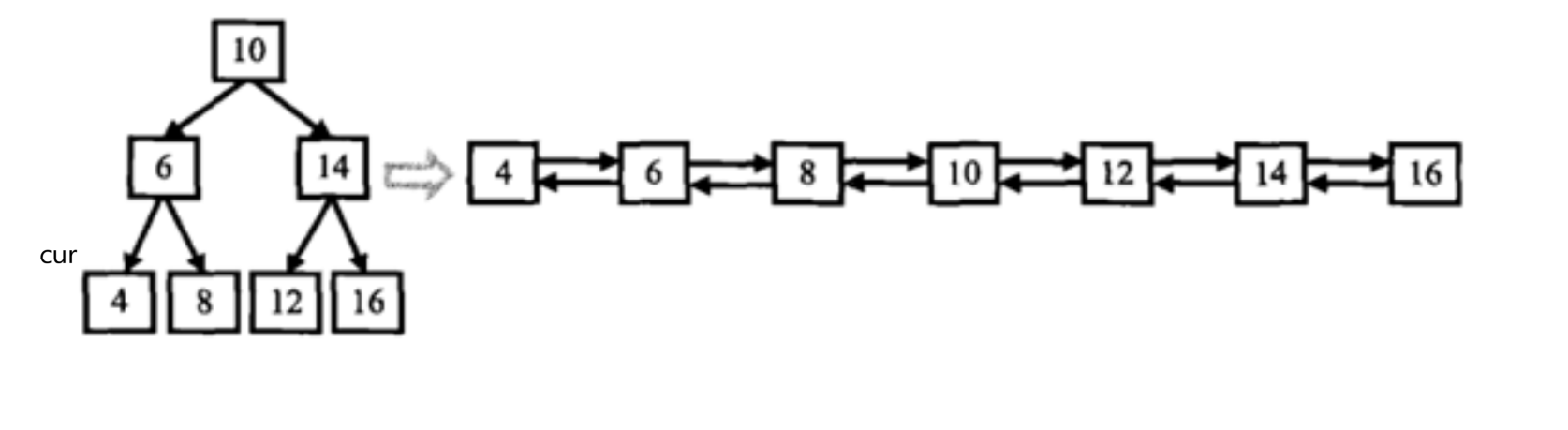
可以中序遍历走，让一个指针的right中序的下一个，left指向中序的上一个。先来写个中序：
cur在允许位置出现的顺序就是有序，现在要想办法让cur的left指向上一个，right指向下一个。那怎么知道上一个或下一个是谁呢？有这样一种方案，再给一个指针叫prev，用来指向上一个访问的结点。prev最开始是空的，在当前cur结点时让左指向prev，cur递归时把cur给prev，再让cur继续往下走，经过这样左指针就全搞定了(prev给引用，否则会坑，下一层指针改的时候不会影响上一层)。现在后继怎么办？这里虽然不知道cur的下一个是谁，但知道上一个的下一个是cur，如：
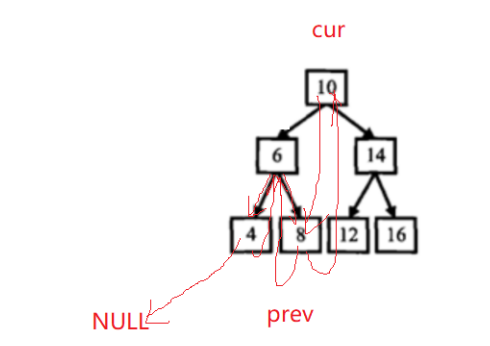
目前不知道10的右是谁，但知道prev(8)的下一个是10，所以可回到cur的上一个，让上一个的right指向cur。所以cur的左指向前一个，前一个的right指向cur，前一个可能为空，所以加一个判断，最后返回开始：
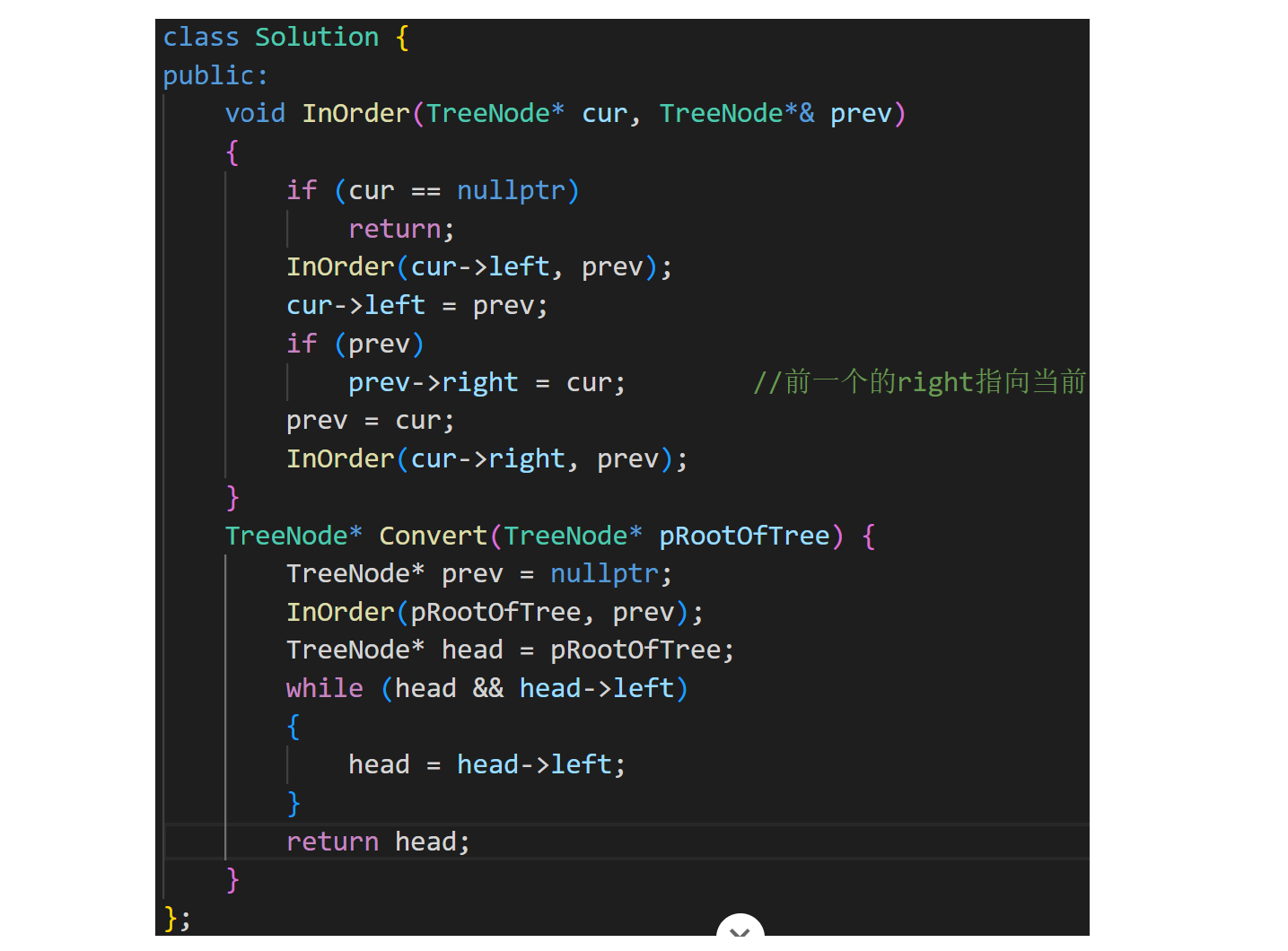
105. 从前序与中序遍历序列构造二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/description/题目要求给了一个前序和中序来构造二叉树。前序可以可以确定根，中序可以分开左右子树区间：
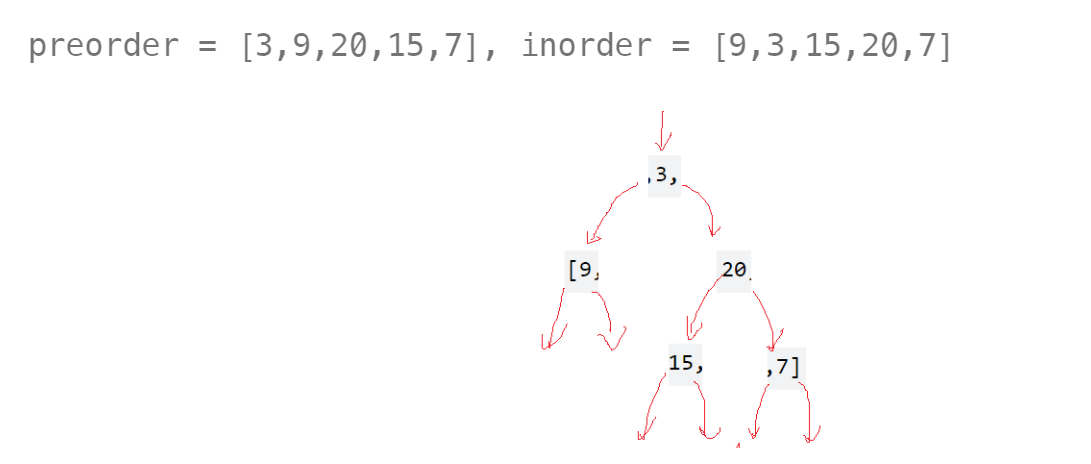
上面根据前序的3确定了根，进而根据中序分出了左子树和右子树区间，此时可通过前序去递归：前序确定根，先递归创建左子树，若为空递归创建右子树。下面来实现：需要一个子函数，因为需要下标，前序用一个下标直接走就行，中序用一个区间。前序进来是根，区分时先找到根这个值的位置，找到后中序被分为三部分：[inbegin, rooti-1] rooti [rooti+1, inend]，好了后++prei，然后递归创建左子树，递归创建右子树，最后返回root。如果中序区间不存在，就不用构建返回空：
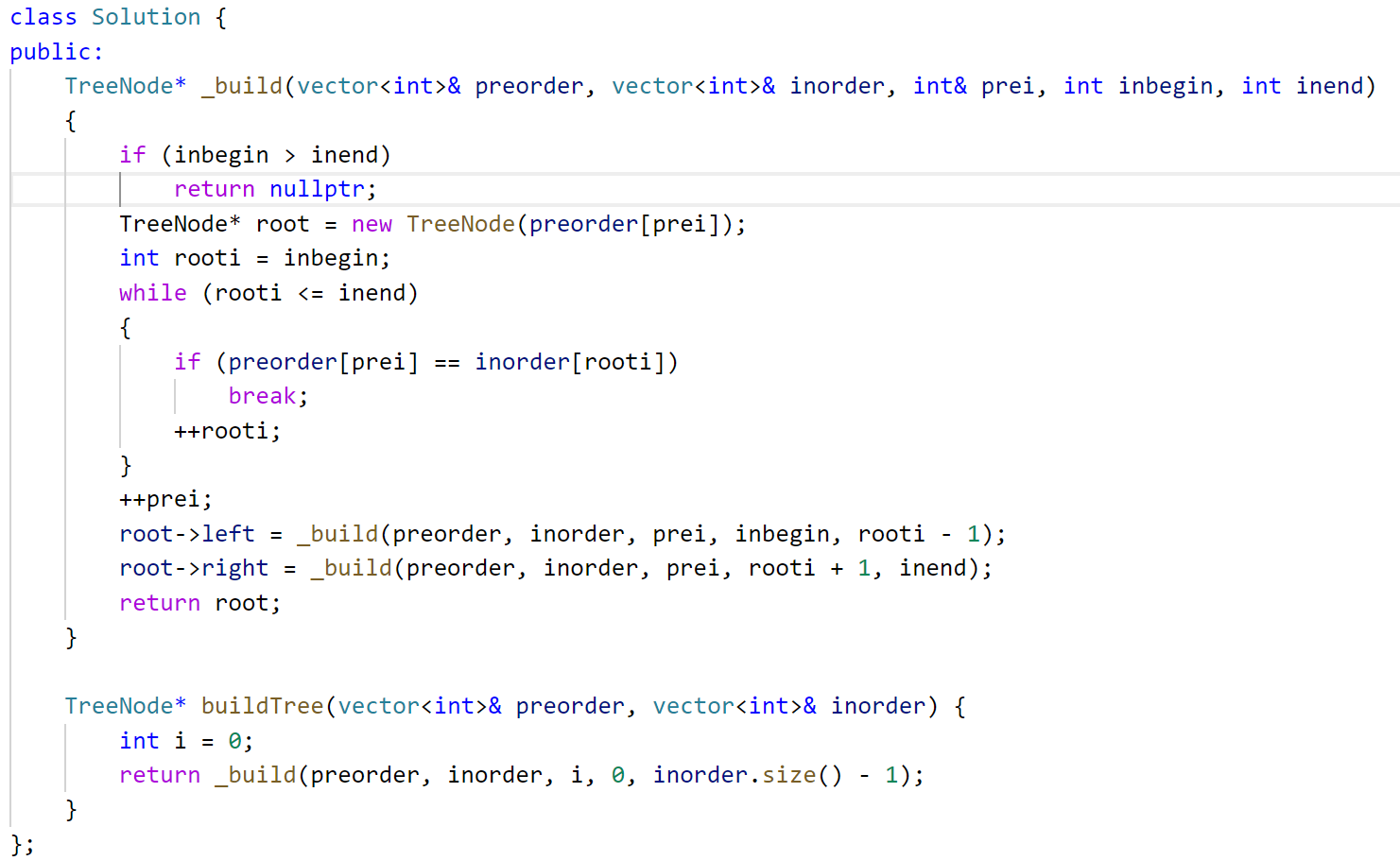
106. 从中序与后序遍历序列构造二叉树 - 力扣（LeetCode）https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal/description/和上一题很像，后序反着来就行：
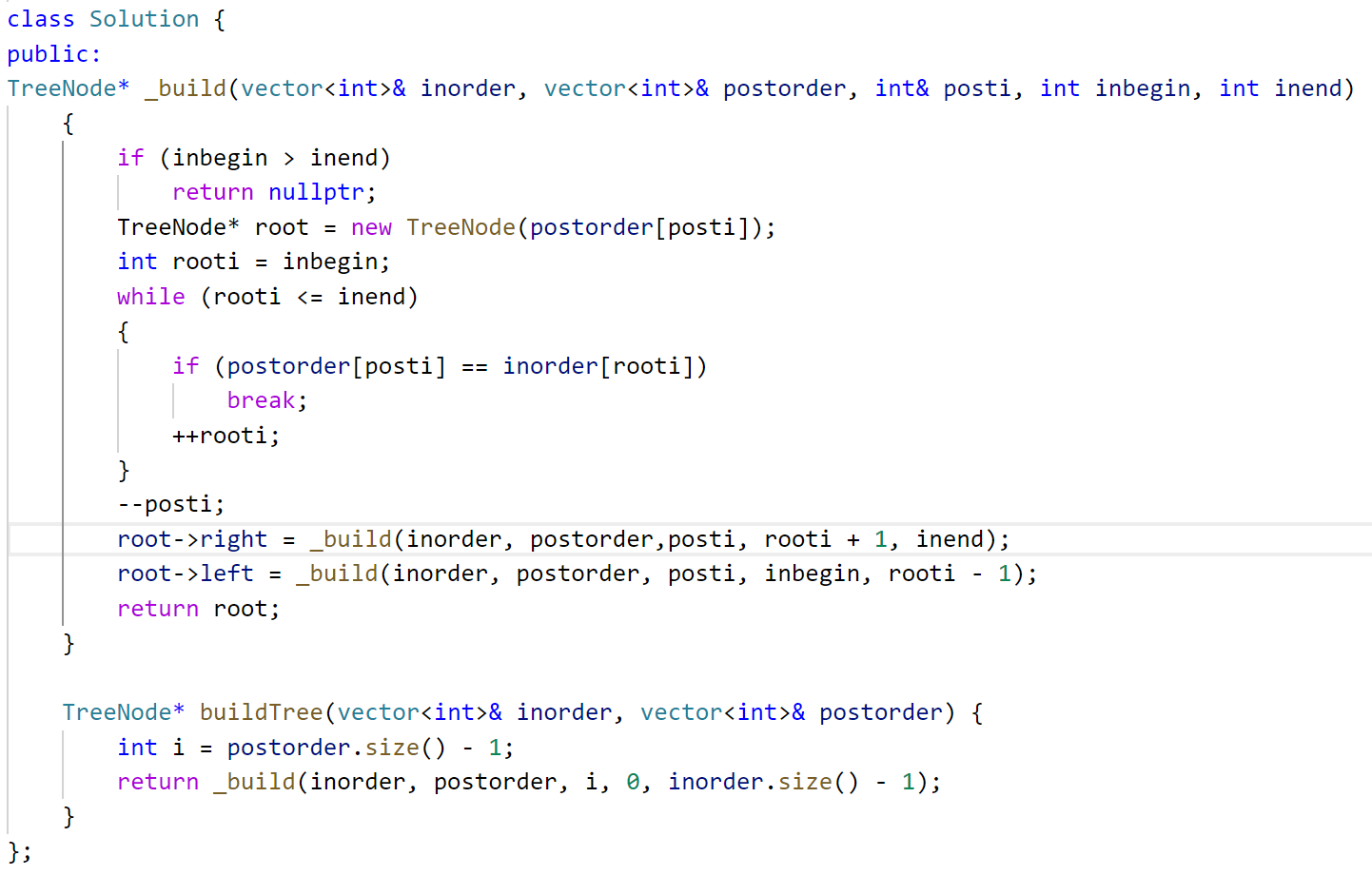
144. 二叉树的前序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-preorder-traversal/description/（非递归）如图：
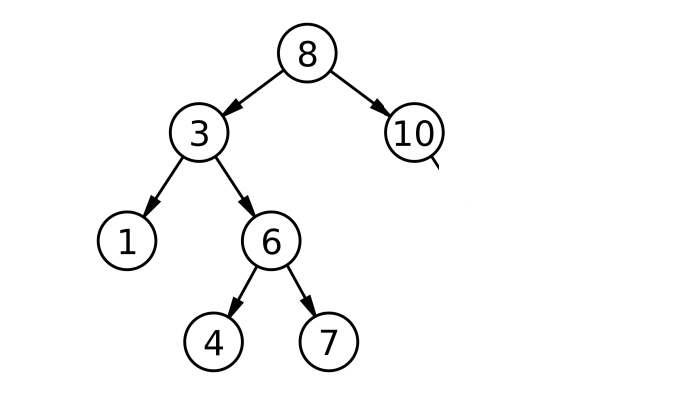
首先一棵树在前序里面能快速访问的是左路结点，剩下没有被访问的是左路结点的右子树。8，3，1完了后访问1的右子树，再访问3的右子树，再访问8的右子树就结束了，那怎样去做呢？可以存到栈里面，第一步访问左路结点同时把左路结点入栈( [8 3 1] )，取结点访问右子树时继续分为访问左路结点和左路结点的右子树，栈为空意味着结束：
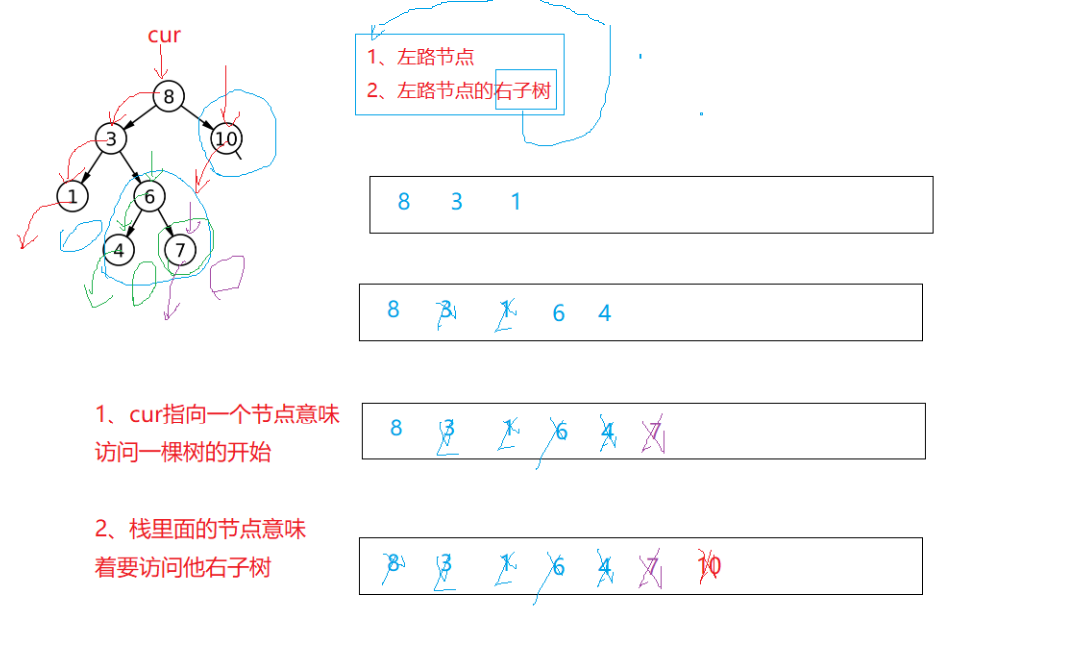
(1.cur指向一个结点意味着访问一棵树的开始。2.栈里面的结点意味着要访问右子树)下面来实现：定义栈，定义cur指向树的开始。循环开始，访问一棵树的开始，先访问左路结点且左路结点入栈，后续依次访问左路结点的右子树，把结点往vector里放同时入栈。入栈的意义是保证依次访问右子树，访问右子树转化为上面的子问题，cur为空不访问，栈不为空就继续：
94. 二叉树的中序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-inorder-traversal/description/中序要左子树访问完才访问右子树，还是分为左路结点和右子树，现在不能访问左路结点，但还得把左路结点入栈。从栈里面取一个结点意味着这个结点左子树已经访问完了，取出来访问结点及结点右子树：
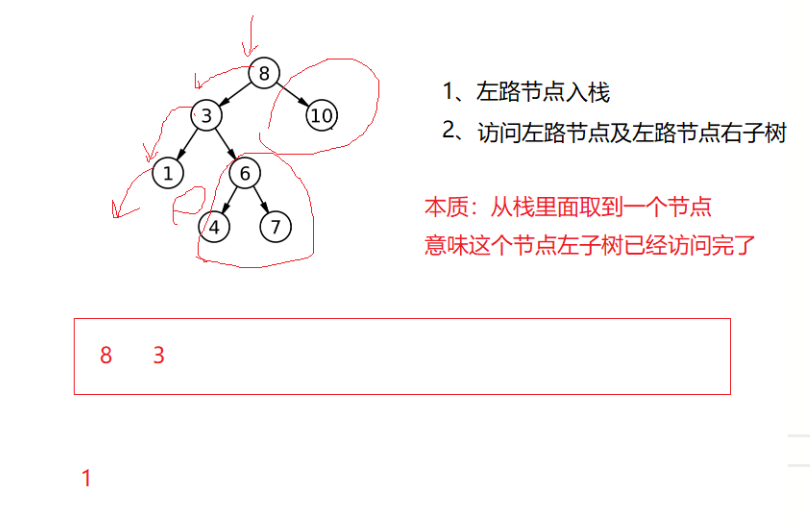
变一下时机就行：
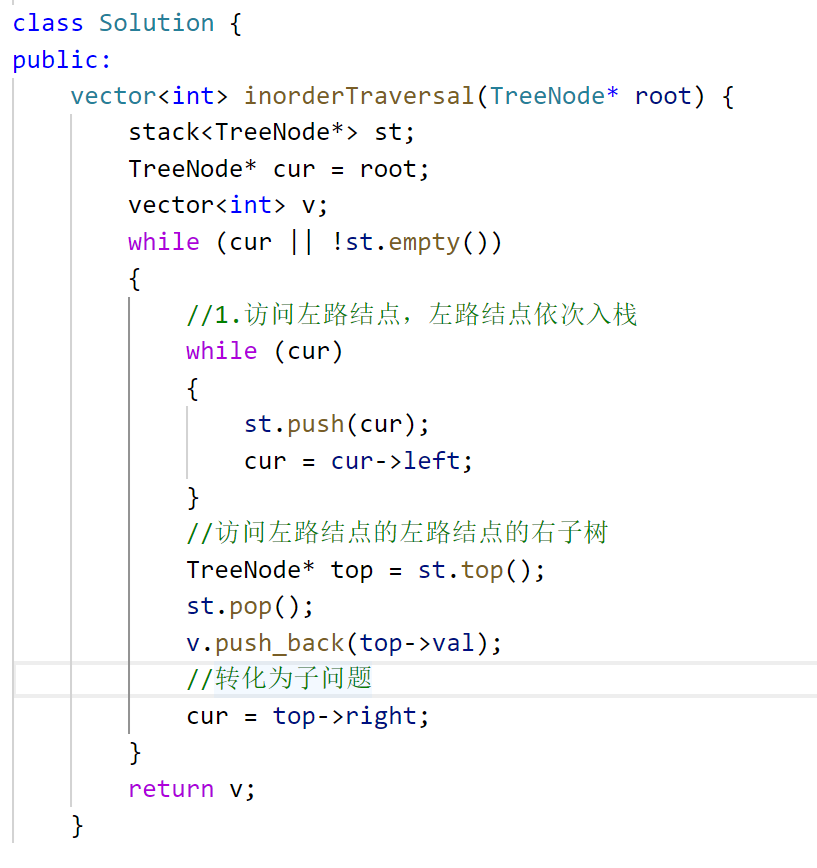
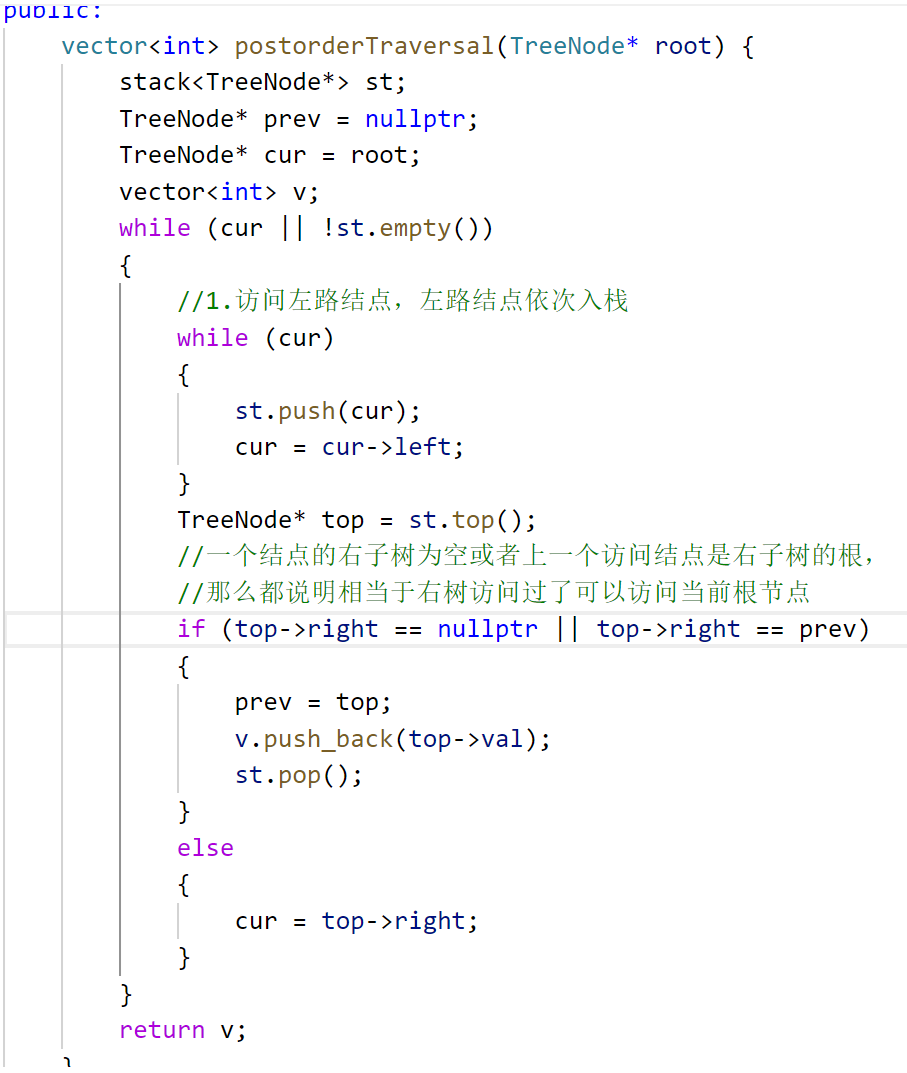
145. 二叉树的后序遍历 - 力扣（LeetCode）https://leetcode.cn/problems/binary-tree-postorder-traversal/description/再看看后续遍历，前面还是一样，左路结点不能访问入栈，但中序出左路结点及左路结点右树，后序呢？后序要把右子树访问完了才能进行访问，如图：
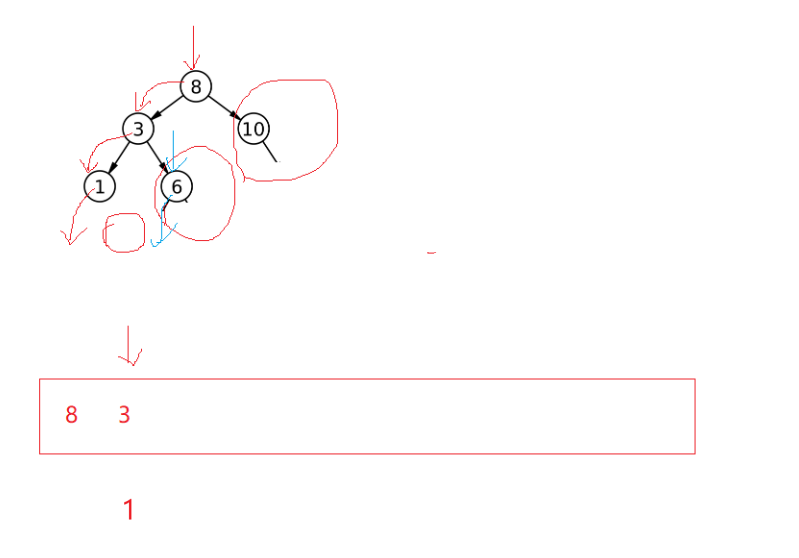
1的右是空1可以访问；3的右不是空要去访问3的右，把6入栈，在栈取6，6的右是空取6。再次到3，这怎么知道3的右已经访问过了？
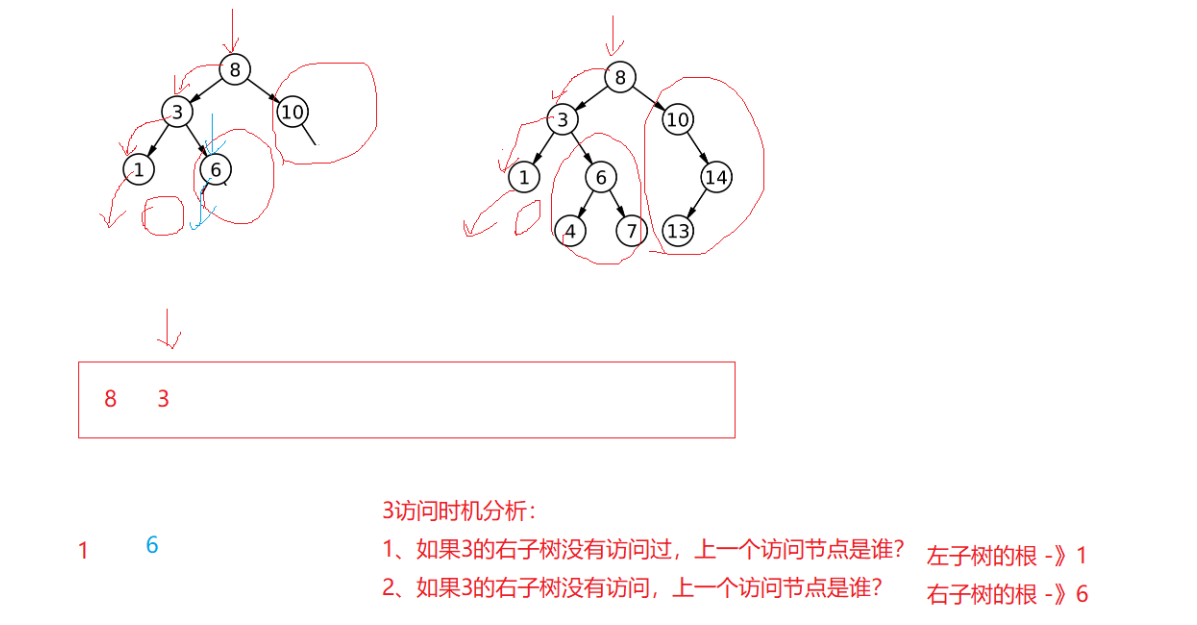
下面来实现：这需要记录前缀结点，遇到左路结点先入栈，然后取栈顶结点，取到这个结点意味着左树访问完了；如果右数为空可以访问，同时把结点从栈里pop掉，每次一个结点要访问先给prev，若不为空先访问右：
