一元函数微分学
一元函数微分学相关命题的常见反例
- 狄利克雷函数: f ( x ) f(x) f(x)不连续
- sin 1 x \sin\frac{1}{x} sinx1(震荡间断点)
下面这题选B,请你为其他三个选项分别举出反例
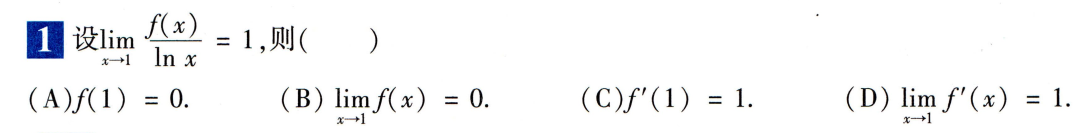

曲率计算公式
直角坐标下的曲率计算公式
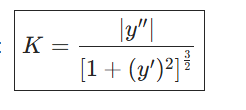
参数方程的曲率计算公式
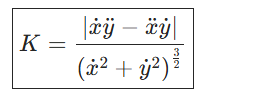
推导过程如下
极坐标下的曲率计算公式
这个我们就是用上面的参数方程公式来做的

微分方程
伯努利方程
伯努利方程的标准形式
一阶伯努利方程的严格定义需满足以下形式:
d y d x + P ( x ) y = Q ( x ) y n \frac{dy}{dx} + P(x)y = Q(x)y^n dxdy+P(x)y=Q(x)yn
伯努利方程的求解关键是通过变量代换 消去非线性的 y n y^n yn项,将其转化为一阶线性方程。具体步骤分为3步,逻辑清晰且具有通用性:
步骤1:消去方程右边的 y n y^n yn项
方程两边同时除以 y n y^n yn(需注意 y ≠ 0 y≠0 y=0,后续需验证y=0是否为解),将方程改写为:
y − n d y d x + P ( x ) y 1 − n = Q ( x ) y^{-n}\frac{dy}{dx} + P(x)y^{1-n} = Q(x) y−ndxdy+P(x)y1−n=Q(x)
步骤2:引入变量代换,转化为线性方程
观察上式, y − n d y d x y^{-n}\frac{dy}{dx} y−ndxdy 可表示为某一新变量导数的"常数倍"。定义新变量:
z = y 1 − n z = y^{1-n} z=y1−n
对z关于x求导(利用复合函数求导法则):
d z d x = ( 1 − n ) y − n d y d x \frac{dz}{dx} = (1-n)y^{-n}\frac{dy}{dx} dxdz=(1−n)y−ndxdy
将 d y d x = 1 1 − n y n ⋅ d z d x \frac{dy}{dx} = \frac{1}{1-n}y^n \cdot \frac{dz}{dx} dxdy=1−n1yn⋅dxdz 代入步骤1的方程,化简后得到:
1 1 − n d z d x + P ( x ) z = Q ( x ) \frac{1}{1-n}\frac{dz}{dx} + P(x)z = Q(x) 1−n1dxdz+P(x)z=Q(x)
两边同乘 ( 1 − n ) (1-n) (1−n),最终转化为一阶线性非齐次微分方程 的标准形式:
d z d x + ( 1 − n ) P ( x ) z = ( 1 − n ) Q ( x ) \frac{dz}{dx} + (1-n)P(x)z = (1-n)Q(x) dxdz+(1−n)P(x)z=(1−n)Q(x)
步骤3:求解线性方程并回代
此时方程已转化为关于 z ( x ) z(x) z(x)的一阶线性方程,记为:
d z d x + P ∗ ( x ) z = Q ∗ ( x ) \frac{dz}{dx} + P^*(x)z = Q^*(x) dxdz+P∗(x)z=Q∗(x)
其中 P ∗ ( x ) = ( 1 − n ) P ( x ) P^*(x) = (1-n)P(x) P∗(x)=(1−n)P(x), Q ∗ ( x ) = ( 1 − n ) Q ( x ) Q^*(x) = (1-n)Q(x) Q∗(x)=(1−n)Q(x)。
这类线性方程的解法是"常数变易法 ",其通解公式为:
z = e − ∫ P ∗ ( x ) d x [ ∫ Q ∗ ( x ) e ∫ P ∗ ( x ) d x d x + C ] z = e^{-\int P^*(x)dx} \left[ \int Q^*(x) e^{\int P^*(x)dx} dx + C \right] z=e−∫P∗(x)dx[∫Q∗(x)e∫P∗(x)dxdx+C]
将 z = y 1 − n z = y^{1-n} z=y1−n回代到上述通解中,即可得到原伯努利方程关于 y ( x ) y(x) y(x)的通解。
最后需补充:若 y = 0 y=0 y=0满足原方程(代入后左右两边均为0),则 y = 0 y=0 y=0也是方程的一个解,需根据初始条件判断是否纳入最终结果。
欧拉方程
1. 标准形式(二阶)
对于自变量 x > 0 x > 0 x>0,方程形式为:
x 2 y ′ ′ + p x y ′ + q y = 0 x^2 y'' + p x y' + q y = 0 x2y′′+pxy′+qy=0
其中:
- y = y ( x ) y = y(x) y=y(x) 是待求函数, y ′ y' y′、 y ′ ′ y'' y′′ 分别是一阶、二阶导数;
- p p p、 q q q 是常数(与 x x x 无关)。
2. 求解方法:变量代换
令 t = ln x t = \ln x t=lnx(即 x = e t x = e^t x=et),将自变量从 x x x 转化为 t t t,利用复合函数求导法则:
- y ′ = d y d x = d y d t ⋅ d t d x = 1 x ⋅ d y d t y' = \frac{dy}{dx} = \frac{dy}{dt} \cdot \frac{dt}{dx} = \frac{1}{x} \cdot \frac{dy}{dt} y′=dxdy=dtdy⋅dxdt=x1⋅dtdy;
- KaTeX parse error: Expected group as argument to '\left' at end of input: ...c{1}{x^2} \left\frac{d2y}{dt2} - \frac{dy}{dt} \right)$。
代入原方程后,可转化为常系数线性微分方程 :
d 2 y d t 2 + ( p − 1 ) d y d t + q y = 0 \frac{d^2y}{dt^2} + (p-1)\frac{dy}{dt} + q y = 0 dt2d2y+(p−1)dtdy+qy=0
再通过求解特征方程(如 r 2 + ( p − 1 ) r + q = 0 r^2 + (p-1)r + q = 0 r2+(p−1)r+q=0)得到通解,最后代回 t = ln x t = \ln x t=lnx 即可。