面试150——动态规划

279.完全平方数

思路

将n看成背包，1~n看成是物品，可重复，完全背包，组合问题，要求恰好装满。

dp[i] = min(dp[i], dp[i - k * k] + 1)
代码

java 复制代码

class Solution {
    public int numSquares(int n) {
        int[] dp = new int[n + 1];
        Arrays.fill(dp, 100010);
        dp[0] = 0;
        for (int i = 1; i <= n; i ++) {
			for (int j = i * i; j <= n; j ++) {
				dp[j] = Math.min(dp[j], dp[j - i * i] + 1);
			}
		}
		return dp[n];
    }
}

139. 单词拆分

思路

字符串s当成是一个背包，字符串列表作为是物品。恰好装满背包，可重复使用则是完全能背包。字符串是由顺序的所以是排列。

代码

java 复制代码

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        // 去重
        Set<String> set = new HashSet<>(wordDict);
        int n = s.length(), m = set.size();
        boolean[] dp = new boolean[n + 1];
        dp[0] = true;
        for (int i = 1; i <= n; i ++) {
        	for(String word : set) {
                int l = word.length();
                if (l <= i) {
                    dp[i] = dp[i - l] & (word.equals(s.substring(i - l, i)));
                    if (dp[i]) break;
                }
        	}
        }
        return dp[n];
    }
}

97. 交错字符串

思路

这也是一道背包题目，s3作为背包。排列s1和s2中的字符（其中交错的是字符串，所以不论怎么），并判断是否能排列成s3。设dp[i, j]表示s1,的1~i, s2的1~j是否能交错组成s3的i + j 。

代码

java 复制代码

class Solution {
    public boolean isInterleave(String s1, String s2, String s3) {
        int n = s1.length(), m = s2.length();
        if ((n + m) != s3.length()) return false;
        boolean[][] dp = new boolean[n + 1][m + 1];
        for (int i = 0; i <= n; i ++) {
            for (int j = 0; j <= m; j ++) {
                int p = i + j - 1;
                if (i == 0 && j == 0) dp[i][j] = true;
                else {
                    if (i - 1 >= 0) dp[i][j] |= (dp[i - 1][j] && s1.charAt(i - 1) == s3.charAt(p));
                    if (j - 1 >= 0) dp[i][j] |= (dp[i][j - 1] && s2.charAt(j - 1) == s3.charAt(p));
                }
            }
        }
        return dp[n][m];       
    }
}

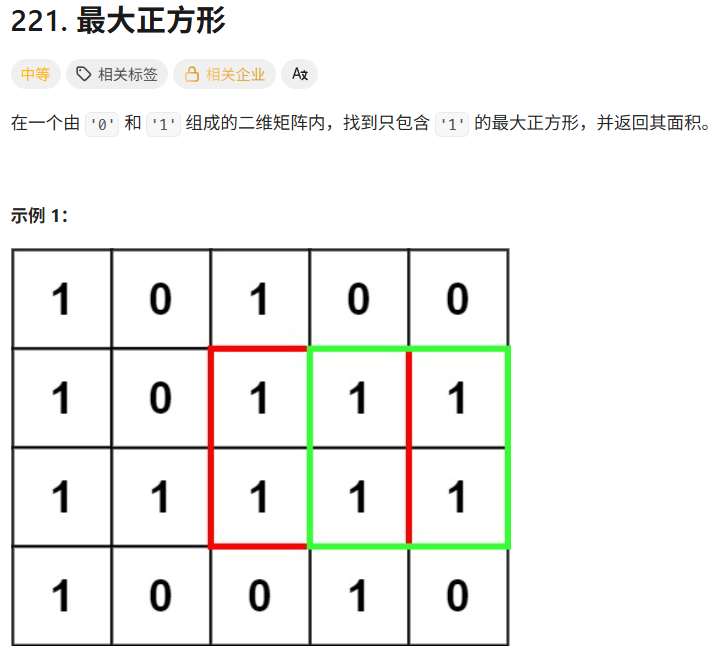
221. 最大正方形

思路

设dp[i, j] 为以(i, j)为右下角的正方形边长的集合。

如果matrix[i,j] = 0, 则dp[i, j] = 0;如果matrix[i, j] = 1，则dp[i, j] = min(dp[i - 1, j], dp[i, j - 1], dp[i - 1, j - 1]) + 1;初始化，将外围初始化为无穷大。

代码

java 复制代码

class Solution {
    public int maximalSquare(char[][] matrix) {
        int n = matrix.length, m = matrix[0].length, MAX_VALUE = Integer.MAX_VALUE - 10, res = 0;
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 0; i <= n; i ++)  Arrays.fill(dp[i], -MAX_VALUE);
        for (int i = 0; i < n; i ++) {
        	for (int j = 0; j < m; j ++) {
        		if (i == 0 && j == 0) dp[i + 1][j + 1] = matrix[i][j] - '0';
        		else {
        			if (matrix[i][j] == '0') dp[i + 1][j + 1] = 0;
        			else {
						int minm = Math.min(dp[i + 1][j], Math.min(dp[i][j + 1], dp[i][j]));
						dp[i + 1][j + 1] = minm < 0 ? 1 : minm + 1;
					}
        		}
                res = Math.max(res, dp[i + 1][j + 1]);  
        	}    		
        }
        return res * res;
        
    }
}

123. 买卖股票的最佳时机 III

思路

状态机模型，dp[i, 0~3]表示第i天的状态，0代表第一次交易持有股票，1代表第一次交易后不持有股票，2表示第二次交易持有股票，3代表第二次交易后不持有股票

dp[i, 0] = max(dp[i - 1, 0), - prices[i]), dp[i, 1] = max(dp[i - 1, 1], dp[i - 1, 0] + prices[i]), dp[i, 2] = max(dp[i - 1, 2], dp[i - 1, 1] - prices[i]), dp[i, 3] = max(dp[i - 1, 3], dp[i - 1, 2] + prices[i])

代码

java 复制代码

// 二维
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length, MAX_INT = 1000010;
        int[][] dp = new int[n + 1][4];
        for (int i = 0; i <= n; i ++) Arrays.fill(dp[i], -MAX_INT);
        for (int i = 1; i <= n; i ++) {
        	dp[i][0] = Math.max(dp[i - 1][0], -prices[i]);
        	dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] + prices[i - 1]);
        	dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] - prices[i - 1]);
        	dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] + prices[i - 1]);
        }
        return Math.max(0, Math.max(dp[i][1], dp[i][3]));
    }
}
// 降维
class Solution {
    public int maxProfit(int[] prices) {
        int n = prices.length, MAX_INT = 1000010;
        int[] dp = new int[4];
        Arrays.fill(dp, -MAX_INT);
        for (int i = 1; i <= n; i ++) {
            dp[3] = Math.max(dp[3], dp[2] + prices[i - 1]);
            dp[2] = Math.max(dp[2], dp[1] - prices[i - 1]);
            dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
        	dp[0] = Math.max(dp[0], -prices[i - 1]);
        }
        return Math.max(0, Math.max(dp[1], dp[3]));
    }
}

188. 买卖股票的最佳时机 IV

思路

也是状态机，只不过天数灵活。定义dp[i, j, 0/1]表示第i天进行第j次交易持有/不持有股票的利润集合

dp[i, j, 0] = max(dp[i - 1, j, 0], dp[i - 1, j - 1, 1] - prices[i]);

dp[i, j, 1] = max(dp[i - 1, j, 1], dp[i - 1, j, 0] + prices[i]);

代码

java 复制代码

class Solution {
    public int maxProfit(int k, int[] prices) {
        int n = prices.length, INT_MAX = -1000010, res = 0;
        int[][][] dp = new int[n + 1][k + 1][2];
        for (int i = 0; i <= n; i ++) 
        	for (int j = 0; j <= k; j ++) {
                Arrays.fill(dp[i][j], INT_MAX);
                dp[i][0][1] = 0;
                }

        for (int i = 1; i <= n; i ++) {
        	for (int j = 1; j <= k; j ++) {
                dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j][0] + prices[i - 1]);
        		dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j - 1][1] - prices[i - 1]);
        		res = Math.max(dp[i][j][1], res);
        	}
		}
		return res;
    }
}