统计学---2.描述性统计-参数估计

总体、个体与样本：
总体，是包含我们要研究的所有数据，总体中的某个数据，就是个体。总体是所有个体构成的集合。从总体中抽取部分个体，就构成了样本，样本是总体的⼀个子集。样本中包含的个体数量，称为样本容量。

**推断统计：**研究如何根据样本数据去推断总体数量特征的方法。它是在对样本数据进行描述的基础上，对统计总体的未知数量特征做出以概率形式表述的推断。

**推断统计意义：**我们为什么要进⾏推断呢？因为在实际的研究中，获取总体数据通常⽐较困难，甚⾄也许是不可能完成的任务。因此，我们就需要对总体进⾏抽样，通过样本的统计量去估计总体参数。也就是说，总体的参数往往是未知的，我们为了获取总体的参数，就需要通过样本统计量来估计总体参数。

点估计与区间估计：

**点估计：**就是使用样本的统计量去代替总体参数。例如，我们要求鸢尾花的平均花瓣⻓度，就可以使⽤样本的均值来估计总体的均值。

点估计实现简单，但是容易受到随机抽样的影响，可能⽆法保证结论的准确性。但是，点估计也并⾮完全⼀⽆是处，因为样本来⾃于总体，样本还是能够体现出总体的⼀些特征的。
**区间估计：**区间估计根据样本的统计量，计算出⼀个可能的区间与概率（信心指数值），表示总体的参数会有多少概率位于该区间中。区间估计指定的区间，我们称为置信区间，而区间估计指定的概率，我们称为置信度。例如，鸢尾花花瓣长度有70%的可能性在3.4cm ~ 3.8cm之间，3.4cm ~ 3.8cm就是置信区间，而70%就是置信度。
点估计与区间估计的说明如：
1. 点估计是使用⼀个值来代替总体参数值：
  1. 优点：能够给出具体的估计值。
  2. 缺点：缺乏准确性。
    python 复制代码
```
# 导入数据，处理数据
data = load_iris()
data = np.concatenate([data.data, data.target.reshape(-1, 1)], axis=1)
data = pd.DataFrame(data, columns=['sepal_length','sepal_width','petal_length','petal_width','type'])

# 点估计
point_estimation = data['sepal_length'].mean()
# print(point_estimation)
```
2. 区间估计是使用⼀个置信区间与置信度，表示总体参数有多少可能（置信度）会在该范围（置信区间）内。
  1. 优点：能够给出合理的范围以及信⼼指数。
  2. 缺点：不能给出具体的估计值。

中⼼极限定理：

定理内容：要确定置信区间与置信度，我们⾸先要知道总体与样本之间，在分布上有着怎样的联系。在数学上，中⼼极限定理给出了很好的解释说明，内容如下：如果总体（分布不重要）均值为u ，⽅差为σ²，我们进⾏随机抽样，样本容量为n，当n增⼤时，则样本均值逐渐趋近服从正态分布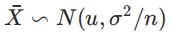：，关于中⼼极限定理，解释如下：

从总体中进⾏多次抽样，则每次抽样会得到⼀个均值，这些均值服从正态分布。

如果总体服从正态分布，则样本容量只需⼤于0即可。
如果总体不服从正态分布，则样本容量通常需要满⾜ n>= 30。
样本均值服从正态分布，该正态分布与总体的关系为：
1. 均值等于总体均值u 。
2. 标准差等于总体标准差σ 除以√n 。
样本均值分布的标准差，我们称为标准误差，简称标准误。

要能够区分总体的标准差，样本的标准差以及标准误。

python 复制代码

# 中心极限定理
# 模拟数据,生成服从对数正态分布的随机数,生成 10000个数据点，作为我们要研究的 "总体"
all_ = np.random.lognormal(size=10000)

# 定义绘图函数,获取样本均值的数据集进行可视化
def plot_dist(all_):
    # 设置不同的样本容量
    sample_num = [1,5,10,30,50,100]
    # 计算理论上的标准误差
    print(all_.std() / np.sqrt(sample_num))
    # 创建画布,3行2列的子图
    fig,ax = plt.subplots(3, 2)
    # 设置画布大小
    fig.set_size_inches(15, 8)
    # 将3x2的子图数组转为1维
    ax = ax.ravel()
    # 循环生成不同样本容量的样本均值分布
    for index, num in enumerate(sample_num):
        # 存储1000个样本均值的数组
        mean_arr = np.zeros(1000)
        for i in range(len(mean_arr)):
            # 每次从总体中随机抽取num个数据（有放回抽样），计算均值并存入mean_arr
            mean_arr[i] = np.random.choice(all_, size=num).mean()
        # 绘制样本均值的直方图和核密度曲线
        sns.histplot(mean_arr, ax=ax[index], kde=True, color='g', alpha=0.6)
        # 设置子图标题，显示样本容量、样本均值的均值、样本均值的标准差
        ax[index].set_title(f'样本容量：{num}\n样本均值的均值：{mean_arr.mean()}:.2f\n样本均值的标准差：{mean_arr.std()}:.2f')
    # 显示图像
    plt.show()
plot_dist(all_)

**正态分布的特性：**之前，我们提到过正态分布，我们知道，在正态分布中，均值，中位数与众数

是相等的。越靠近均值的数据越多，反之越少。接下来，我们来给出具体的分布比例情况，如下图：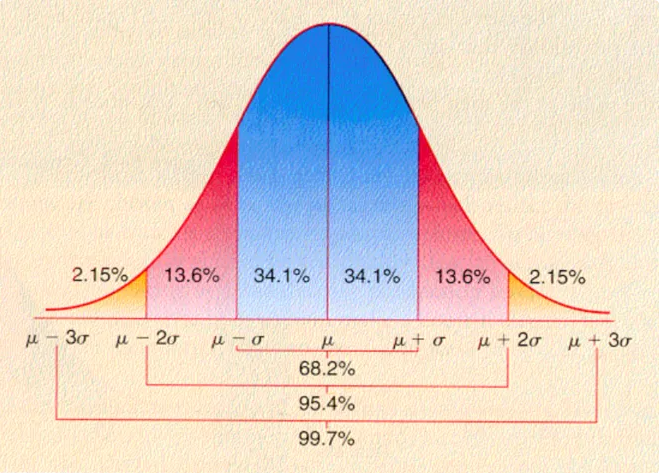

在正态分布中，数据的分布比例如下：

以均值为中心，在1倍标准差内，包含约68%的样本数据。
2. 以均值为中心，在2倍标准差内，包含约95%的样本数据。

以均值为中心，在3倍标准差内，包含约99.7%的样本数据。

python 复制代码

# 正态分布的概率
# 生成正态分布数据,设定标准差（σ）为50
scale = 50
# 生成10万个服从正态分布的随机数
x = np.random.normal(0, scale, size=100000)
# 循环计算不同倍数标准差范围内的数据比例，循环3次，分别计算1倍、2倍、3倍标准差范围
for i in range(1,4):
    # 筛选出落在 [-times*scale, times*scale] 范围内的数据
    y = x[(x > -i * scale) & (x < i * scale)]
    # 输出该范围内的数据占总数据的百分比
    print(f'{i}倍标准差')
    print(f'{len(y) * 100 / len(x)}%')

通常，我们以2倍标准差作为判定依据，则以样本均值为中心，正负2倍标准差构成的区间，就是置信区间。而2倍标准差包含了95%的数据，因此，此时的置信度为95%。换⾔之，我们有95%的信心认为，总体的均值会在置信区间之内。

python 复制代码

mean=np.random.randint(-10000,10000)
# 总体的标准差
std=50
# 总体
all_=np.random.normal(loc=mean,scale=std,size=10000)
# 从总体抽50个数据形成样本
sample=np.random.choice(all_,size=50)
# 样本的均值
sample_mean=sample.mean()
print('样本的均值:',sample_mean)
# 标准误差
se=std/np.sqrt(50)
# 求置信区间
min_=sample_mean-1.96*se 
max_=sample_mean+1.96*se
# print((min_,max_))