在机器学习/深度学习模型中,有两类参数:
| 类型 | 定义 | 例子 | 是否通过训练自动更新 |
|---|---|---|---|
| 模型参数(parameters) | 模型内部可学习的数值 | 权重、偏置 | 会被优化器更新 |
| 超参数(hyperparameters) | 训练前由人设定的控制变量 | 学习率、batch size、网络深度 | 不会自动更新,要人为选择 |
例如,神经网络中的学习率和神经元数量,或支持向量机中的核函数大小,都会显著影响模型的训练效果和泛化能力。
超参数调整 就是"如何最优地训练神经网络"的艺术与科学,目标就是 寻找一组最优的超参数 ,使 模型表现最好 的过程。
自动调参方法 :随机搜索、网格搜索、贝叶斯优化 等。
神经网络包含哪些超参数?
通常可以分为三类:网络参数、优化参数、正则化参数。
- 网络参数 :卷积核的数量 和 尺寸 (3×3、5×5)、全连接层节点数 、网络层数 (深度)和 激活函数 (ReLU、LeakyReLU、)、池化类型和参数 (最大池化、平均池化、步长)、层间连接方式 (串接 stacking、跳跃连接 residual、注意力机制)、嵌入维度 (Embedding size)、多头注意力的头数 、Transformer 层数 等。
- 优化参数 :学习率 (learning rate)、批样本数量 (batch size)、训练轮数 (epochs)、优化器选择 (SGD, Adam, AdamW, RMSProp)动量 (momentum,适用于 SGD 等优化器)、梯度裁剪(gradient clipping)阈值、部分损失函数的可调参数。
- 正则化参数 (用来控制过拟合):权重衰减 (weight decay / L2 正则化)、丢弃率 (dropout rate)、数据增强策略及参数 (如旋转角度、裁剪比例等)、早停 (early stopping)、指数移动平均(EMA)权重。
- 其他可能的超参数 :权重初始化方法 (Xavier、He 等)、嵌入/编码策略 (特别是 NLP 模型)、学习率 warm-up 参数 、混合精度训练(FP16)相关参数。
| 类别 | 超参数 | 常见选项 / 说明 | 作用 |
|---|---|---|---|
| 网络结构参数 | 层类型 | 卷积层、全连接层、循环层、注意力层等 | 决定网络结构和特征抽取方式 |
| 层数 | 1,2,...n | 控制网络深度和表达能力 | |
| 神经元/通道数 | 卷积核数量、全连接节点数 | 决定每层容量和特征维度 | |
| 卷积核大小 | 3×3, 5×5, 7×7 | 控制局部感受野 | |
| 激活函数 | ReLU, LeakyReLU, GELU, Sigmoid, Tanh | 引入非线性,提高表达能力 | |
| 层间连接方式 | 串接、残差、跳跃、注意力机制 | 控制信息流和梯度传播 | |
| 池化类型及参数 | 最大池化、平均池化、步长 | 降维和提取特征不变性 | |
| 嵌入维度 | Embedding size(NLP/图神经网络) | 决定特征表示维度 | |
| 注意力参数 | 多头数量、Transformer层数 | 控制全局信息交互能力 | |
| 优化参数 | 学习率 | 固定、衰减、cosine annealing、warm-up | 控制梯度更新幅度 |
| 优化器 | SGD, Adam, AdamW, RMSProp | 控制梯度更新策略 | |
| 批次大小 | 16, 32, 64, 128... | 控制训练稳定性和内存占用 | |
| 训练轮数 | epoch 数 | 决定训练迭代次数 | |
| 动量 | 0~1 | 平滑梯度更新,提高收敛速度 | |
| 梯度裁剪 | 阈值 | 防止梯度爆炸 | |
| 损失函数可调参数 | Focal Loss γ、α | 调整损失敏感度 | |
| 正则化参数 | 权重衰减 | L2 正则化系数 | 降低过拟合 |
| 丢弃率 | Dropout 0~1 | 随机屏蔽神经元,防止过拟合 | |
| 数据增强参数 | 翻转、裁剪、旋转、颜色扰动 | 提升模型泛化能力 | |
| 早停 | patience | 防止训练过度拟合 | |
| EMA | 指数移动平均权重 | 平滑模型参数,提高泛化 | |
| 归一化参数 | BatchNorm、LayerNorm momentum/eps | 稳定训练,部分起正则化作用 | |
| 其他超参数 | 权重初始化 | Xavier, He, Kaiming | 控制初始梯度分布 |
| 混合精度训练 | FP16/FP32 | 提升训练效率,减少显存占用 |
如何选择激活函数?
如果不确定哪一个激活函数效果更好,就都试试,在验证集评价选择表现更好的那个。
-
如果是 二分类问题 (输出是 0、1 值),输出层选择 sigmoid 函数 (常配合 二元交叉熵损失 Binary Cross-entropy 使用),其他的所有单元都选择 ReLU 函数。
-
如果 在隐藏层上不确定使用哪个激活函数,通常使用 ReLU 激活函数,有时也会使用 tanh 激活函数,但 ReLU 的一个优点是:当是负值时,导数等于 0。
- tanh 激活函数的输出在 -1 到 1 之间 ,中心化特性有助于梯度下降 ,但可能会出现 梯度消失问题。
- ReLU 在 负值区域导数为 0 ,这能带来 稀疏激活 的效果,训练更快且缓解梯度消失问题,但也容易导致 死神经元问题(某些神经元永远不更新)。
-
如果 遇到了一些死的神经元,可以使用
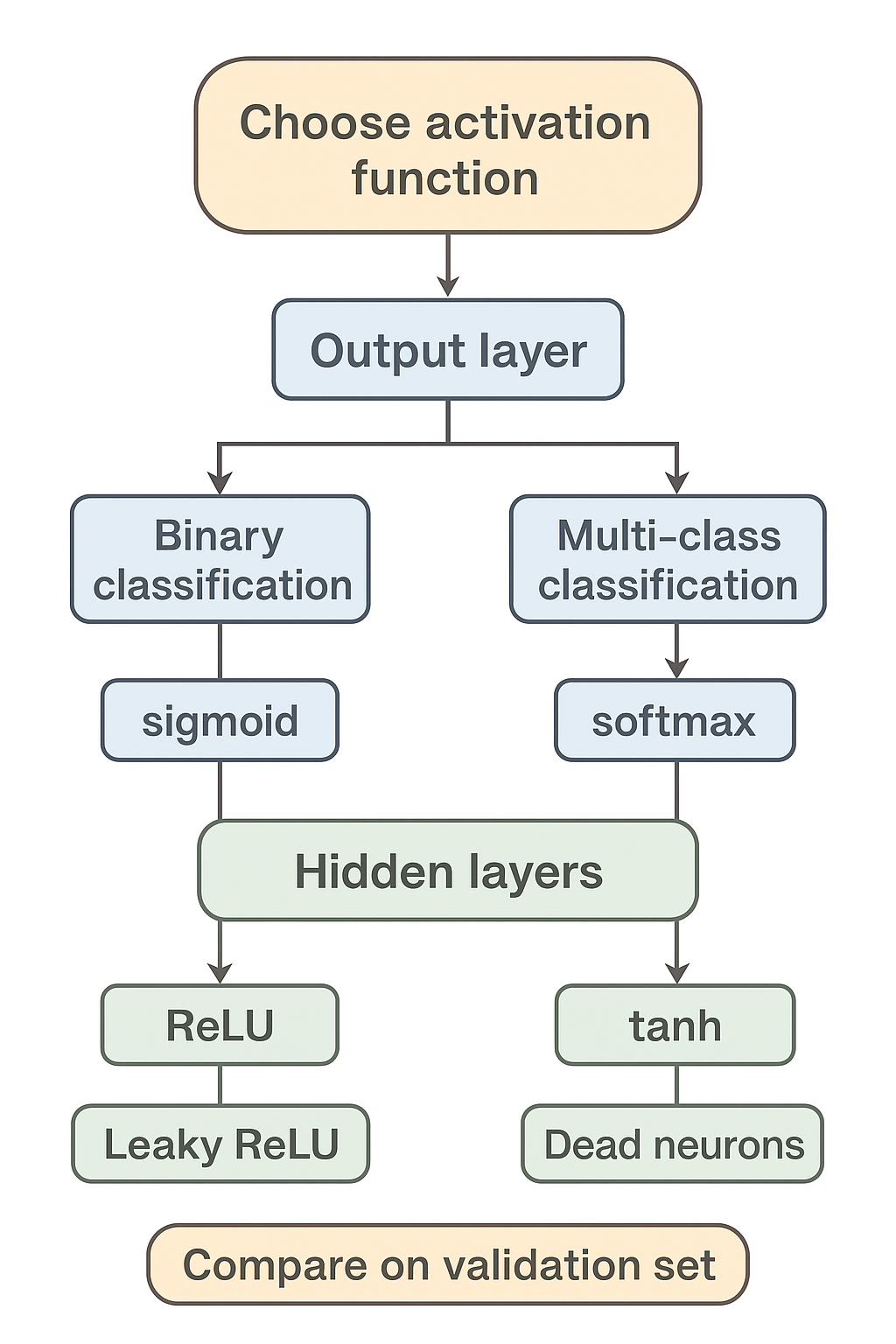
Leaky ReLU 函数 。Leaky ReLU 允许负值有一个很小的斜率(比如 0.01),避免神经元完全不更新。
如何调整 Batch Size?
Batch Size 是指 每次网络前向和反向传播中处理的数据样本数量。根据显卡显存情况,一般用 32/64 倍数调整。
- 随着 Batch Size 增大,处理相同数据量的训练速度越快 。
- 当 batch 很小的时候,GPU 的计算单元很多可能处于空闲状态,资源利用率低;当 batch 增大时,GPU 可以充分利用更多核心同时计算,从而整体吞吐量提升。
- 每个 batch 都要做一次数据加载、数据拷贝到 GPU 和内存管理。Batch 越大,单位样本的这些开销越小(因为多条数据一起处理)。
- Batch Size 大意味着 优化器每做一次梯度更新,可以覆盖更多样本。
- 随着 Batch Size 增大,达到相同精度所需要的 epoch 数量越多 。
-
小 Batch :梯度噪声大 → 参数更新轨迹更"抖动",带来随机扰动 → 有利于跳出局部最优,往往 泛化能力更好 → 少量 epoch 就能达到较高测试精度
-
大 Batch :梯度噪声小 → 参数更新稳定,轨迹平滑 → 容易陷入局部最优,泛化能力可能下降 → 收敛到的精度可能不如小 batch,需要更多 epoch 或特殊策略(如学习率衰减、warmup、动量修正)才能收敛到相同测试精度
-
这两种因素是矛盾的:一方面你想大 batch 提升速度,一方面又不能太大,否则泛化性能和最终精度下降。
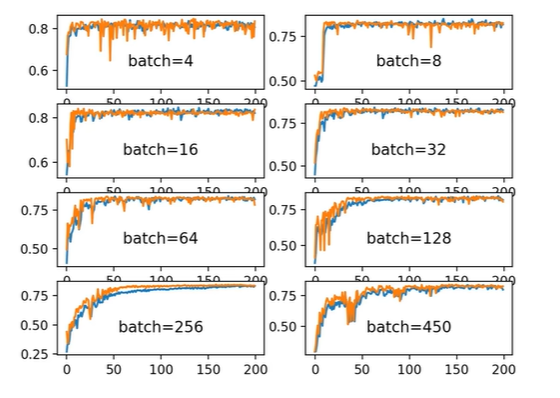
总结 :大 batch 提升的是 吞吐量 (单位时间处理样本多),但损失了 每步探索空间的随机性,所以总 epoch 数可能增加。
当显存不够大 batch 时,可以通过 梯度累积 模拟更大的 batch。
有效 batch =train_batch_size×gradient_accumulate_every
如何调整学习率?
学习率是模型的首要且最重要的参数之一,也是在开始构建模型时几乎必须立即考虑的参数。
梯度下降通过多次迭代,并在每一步中最小化成本函数来估计模型的参数。学习率控制 模型的学习进度。
扩散模型通常对学习率比较敏感,1e-4 是常见的起始值。
一旦确定了批量大小,就该选择与该值最匹配的学习率了。这是 一维参数搜索(即在优化问题中再进行一次优化),并且相对昂贵,因为每次调整学习率都需要重新训练整个网络一次。
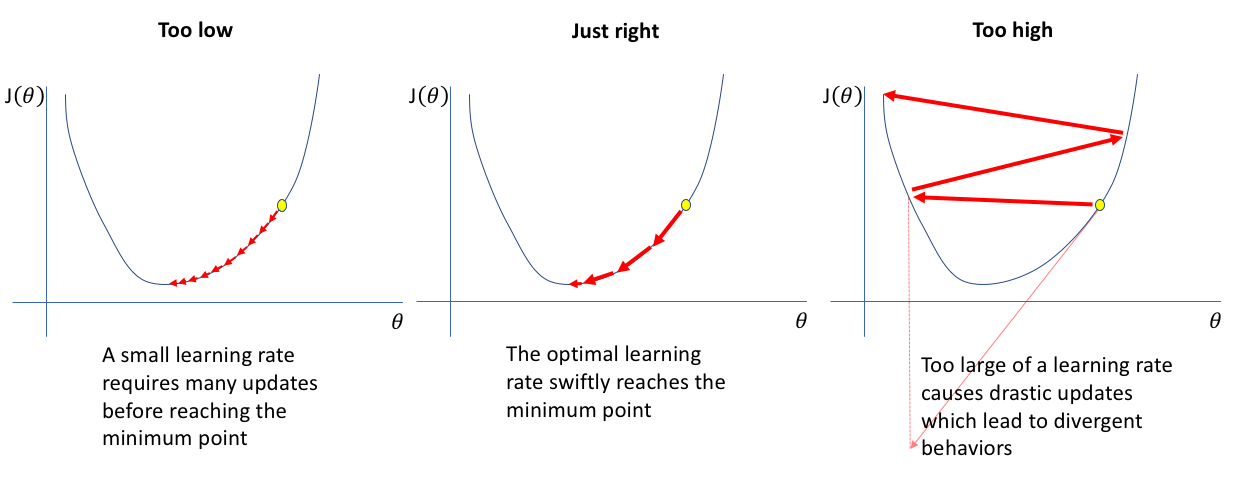
如果你选择一个特定的批量大小,然后绘制模型在使用一系列学习率完全训练后得到的整体损失,这就是你得到的曲线,

这条曲线由三个截然不同的部分组成:
- 学习率太慢,导致学习不足,且对模型没有任何帮助;
- 最陡下降区,最终引导至最佳或接近最佳的学习率。
- 越过曲线的边缘会出现噪声,最终导致发散(这时学习率过大)。
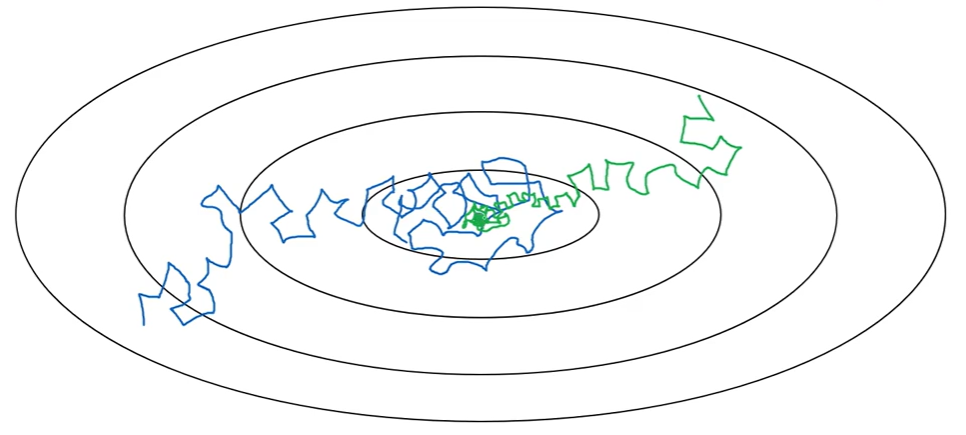
- 在迭代优化的前期,学习率较大则步长较长,可以较快地进行梯度下降;
- 而在迭代优化的后期,逐步减小学习率的值,减小步长,有助于算法的收敛,更容易接近最优解。
实例
下面是一个 Diffusion model 的训练配置,
python
train_batch_size = 16,
train_lr = 1e-4,
train_num_steps = 100000,
gradient_accumulate_every = 1,
ema_update_every = 16,
ema_decay = 0.995,
adam_betas = (0.9, 0.99),
# optimizer & scheduler
self.opt = Adam(diffusion_model.parameters(), lr = train_lr, betas = adam_betas)
self.scheduler = CosineAnnealingLR(self.opt, T_max=10000, eta_min=0) train_lr = 1e-4→ 学习率1e-4,学习率过大 → 容易发散;学习率过小 → 收敛慢 。扩散模型通常对学习率比较敏感,1e-4是常见的起始值。train_num_steps = 100000,总训练步数为 100,000。步数太少 → 模型未充分训练。步数过多 → 可能过拟合 或浪费计算资源。gradient_accumulate_every = 1:梯度累积次数。当显存不够大 batch 时,可以通过梯度累积模拟更大的 batch。这里为 1,表示每步梯度更新一次,不做累积。有效batch = train_batch_size × gradient_accumulate_every。
EMA (Exponential Moving Average) 参数:
ema_update_every = 16:每 16 步更新一次 EMA 权重。EMA 权重是模型参数的滑动平均,通常用于生成阶段,以提高样本质量。ema_decay = 0.995:EMA 衰减系数。EMA 新值 = decay × EMA_old + (1 - decay) × model_new,0.995 表示过去模型权重占比大,新权重占比小。值接近 1 → EMA 更平滑,保留长期历史。 值过小 → EMA 跟随模型波动太快,失去稳定性。
Adam 是常用优化器,结合了 动量 (momentum)和 自适应学习率(adaptive LR)。
Adam 优化器参数:
lr=train_lr→ 学习率 1e-4betas=(0.9, 0.99),0.9→ 一阶动量系数 (momentum),0.99→ 二阶动量系数(RMSprop 类似),beta1 控制梯度一阶矩估计的平滑程度,beta2 控制梯度二阶矩估计的平滑程度。
常用配置 (0.9, 0.99) 对生成模型训练稳定性较好。
CosineAnnealingLR :余弦退火学习率调度器,学习率按余弦曲线从初始 lr 降到 eta_min,然后可能重启。
T_max=10000→ 一个 完整周期的步数(cosine 完整下降周期)eta_min=0→ 最低学习率为 0
公式 :
l r t = η min + 1 2 ( l r initial − η min ) ( 1 + cos t π T max ) lr_t = \eta_{\min} + \frac{1}{2} (lr_{\text{initial}} - \eta_{\min}) \left(1 + \cos\frac{t \pi}{T_{\max}}\right) lrt=ηmin+21(lrinitial−ηmin)(1+cosTmaxtπ)
初期快速收敛,中期慢慢减小学习率,防止过冲。有助于训练生成模型的稳定性和收敛质量。
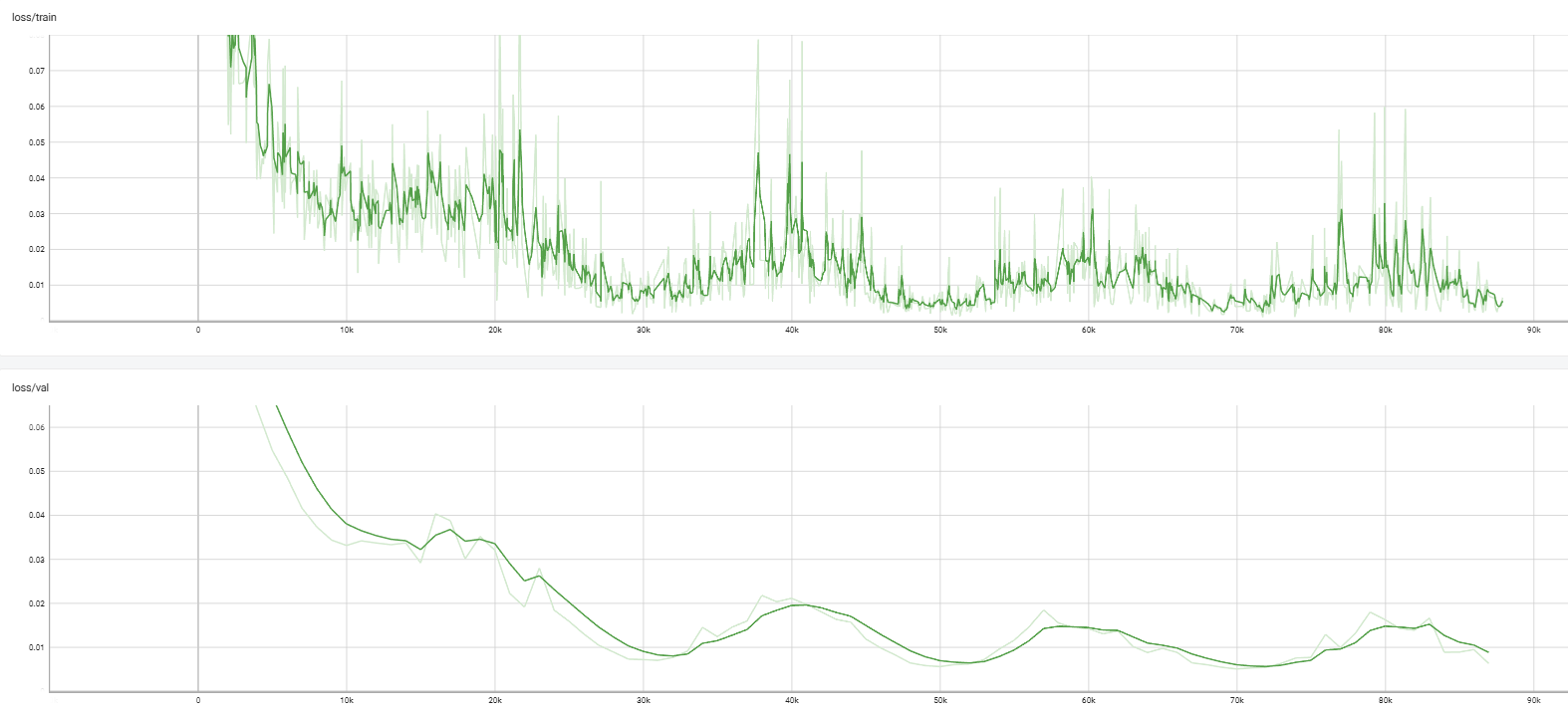
训练 loss:
-
前期下降快,之后出现明显波动。
-
后期仍有小幅度震荡,说明梯度噪声可能较大。
为什么 validation loss 会升高?可能原因如下:
| 原因 | 解释 |
|---|---|
| 过拟合 | 训练集学得太细,验证集误差反而变大 |
| 学习率过高 | 参数更新震荡,导致 loss 波动 |
| 验证集本身随机性 | diffusion loss 里有随机噪声采样,存在波动 |
| batch size 太小 | 统计不稳定导致波动 |
| 模型 capacity 大 | 参数多时过拟合更明显 |
Diffusion 训练里:每步随机采样 noise level t t t、每步加随机噪声 ϵ \epsilon ϵ,Loss 本身带随机性,会自然震荡,所以 diffusion loss 不会线性下降,是波浪下降。
小 batch 会增加梯度噪声,导致训练 loss 波动明显。令 train_batch_size = 128,
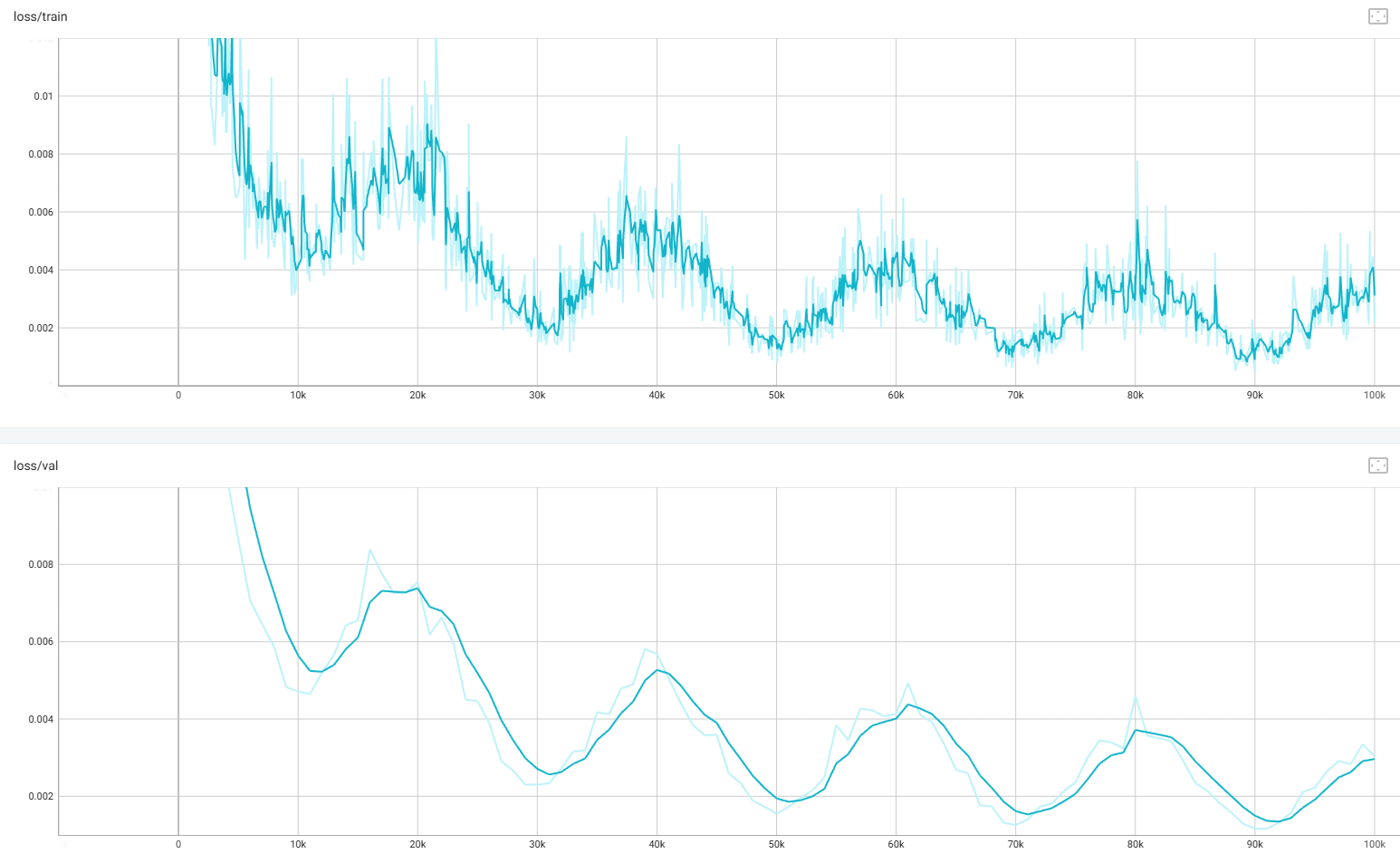
判断训练 diffusion model(或其他深度模型)轮次是否足够,不能只看 epoch 数,训练 loss & 验证 loss 都不再明显下降 (前期下降较快,到中后期变缓,后期几乎横盘 or 小抖动),如果 val loss 先降后升 → 过拟合开始,训练足够了(或早停)。
Diffusion 很关键的一点:最终看生成效果,不只看 loss 。Loss 有时不变,但生成质量仍继续提升,这一点 diffusion 很典型。
| 阶段 | Loss 变化 | 解释 |
|---|---|---|
| 停在局部最优 | 稳定/轻微波动 | 模型"卡住"了 |
| 跳出局部最优 | 短暂上升 | 参数离开局部谷底 |
| 找到更好方向 | 下降 | 进入更深的"谷底" |
| 没找到更好方向 | 继续震荡或更差 | 可能进入另一个次优状态 |