面试150——字典树

208. 实现 Trie (前缀树)

思路

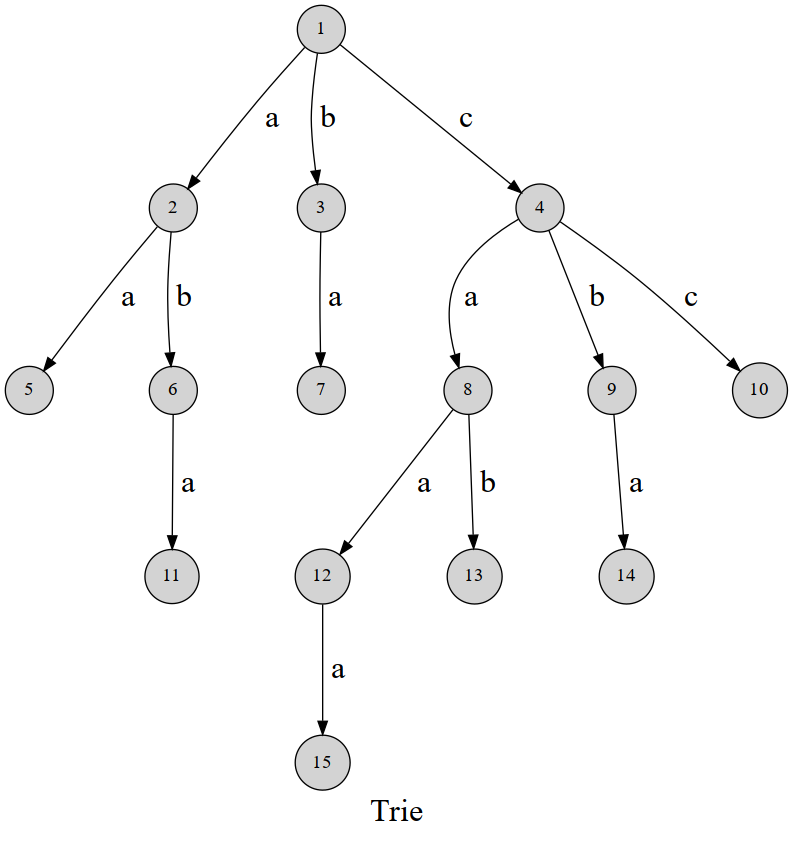
字典树的每条边代表一个字符，从根节点到某一节点的路径表示一个字符串。如果某节点被标记为结束节点，则表示该路径对应的字符串存在于集合中。

代码

java 复制代码

class Trie {
    Trie[] children;
    boolean isEnd;
    public Trie() {
        children = new Trie[26];
        isEnd = false;
    }
    
    public void insert(String word) {
        Trie node = this; // 获取当前节点
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.children[index] == null) node.children[index] = new Trie();
            node = node.children[index];
        }
        node.isEnd = true;
    }
    
    public boolean search(String word) {
        Trie node = this;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.children[index] == null) return false;
            node = node.children[index];
        }
        return node.isEnd;
    }
    
    public boolean startsWith(String prefix) {
        Trie node = this;
        for (char c : prefix.toCharArray()) {
            int index = c - 'a';
            if (node.children[index] == null) return false;
            node = node.children[index];
        }
        return true;
    }
}

211. 添加与搜索单词 - 数据结构设计

思路

addWord就是正常的insert方法，search由于存在'.'代表任何一个数字，因此需要特判，分多种情况往下搜索dfs。
代码

java 复制代码

class WordDictionary {
    WordDictionary[] children;
    boolean isEnd;
    public WordDictionary() {
        children = new WordDictionary[26];
        isEnd = false;
    }
    
    public void addWord(String word) {
        WordDictionary node = this;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.children[index] == null) node.children[index] = new WordDictionary();
            node = node.children[index];
        }
        node.isEnd = true;
    }
    
    public boolean search(String word) {
        return dfs(this, word, 0);
    }

    public boolean dfs(WordDictionary root, String word, int index) {
        if (index == word.length()) {
            return root.isEnd;
        }
        char c = word.charAt(index);
        boolean flag = false;
        if (c != '.') {
            int i = c - 'a';
            if (root.children[i] == null) flag |= false;
            else flag |= dfs(root.children[i], word, index + 1);
        } else {
            for (int i = 0; i < 26; i ++) {
                if (root.children[i] == null) flag |= false;
                else flag |= dfs(root.children[i], word, index + 1);
            }
        }
        return flag;
    }
}

212. 单词搜索 II

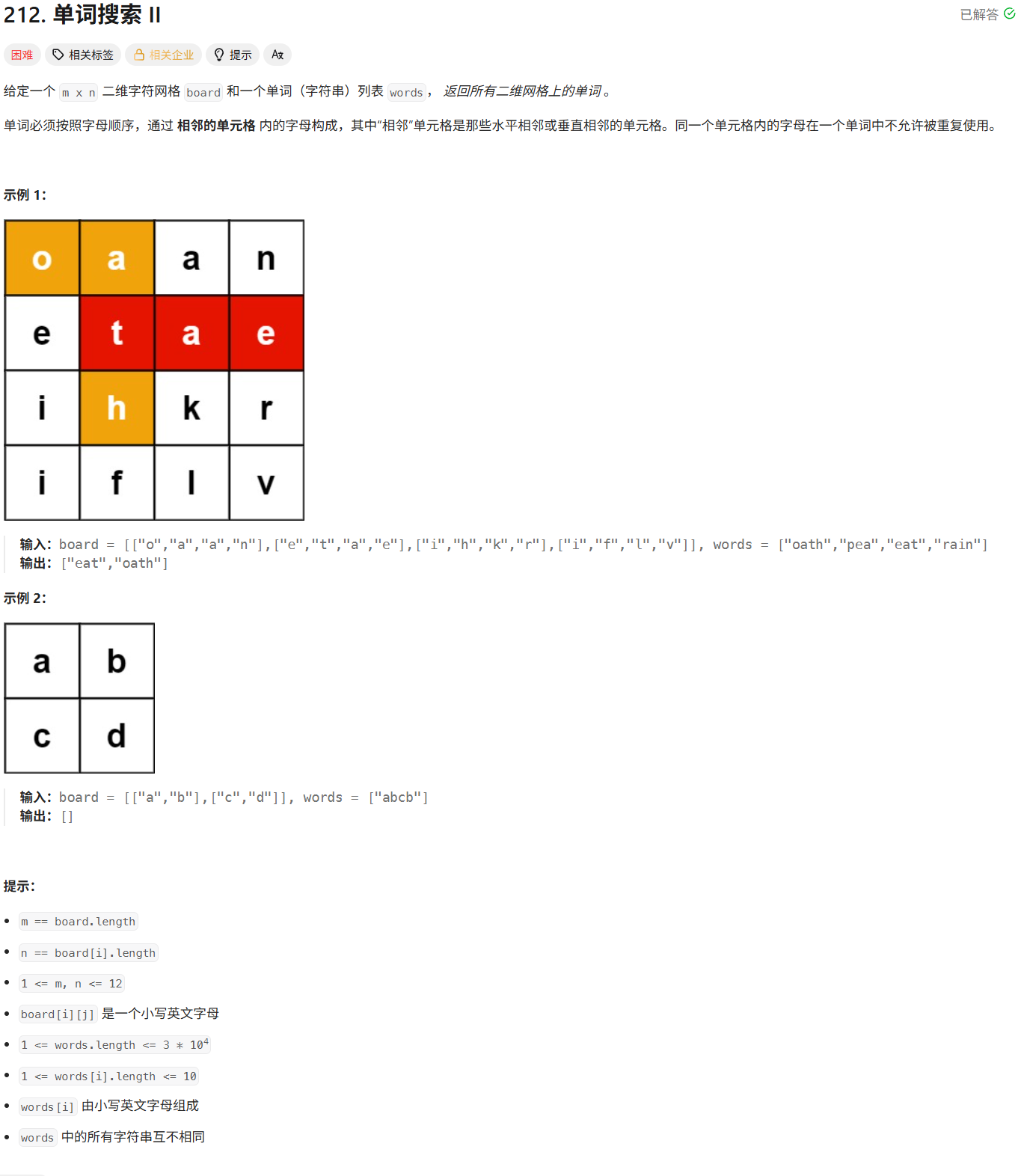
思路

创建字典树，将单词列表的单词都添加到字典树中。之后在网格中全局搜索，以某个位置为起点搜索全网格，之后判断当前字符串是否在字典树中。
代码

java 复制代码

class Solution {
    Set<String> res;
    StringBuilder path;
    Trie trie; 
    int[][] directions = new int[][] {{-1, 0}, {1, 0}, {0, 1}, {0, -1}};
    boolean[][] used;
    public List<String> findWords(char[][] board, String[] words) {
        int n = board.length, m = board[0].length;
        path = new StringBuilder();
        trie = new Trie();
        res = new HashSet<>();
        used = new boolean[n][m];
        for (String word : words) trie.insert(word);
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < m; j ++) {
                char c = board[i][j];
                int index = c - 'a';
                if (trie.children[index] != null) {
                    used[i][j] = true;
                    path.append(c);
                    backtrace(board, i, j, trie.children[index]);
                    path.deleteCharAt(path.length() - 1);
                    used[i][j] = false;
                }
            }
        }
        return new ArrayList<>(res);
    }

    void backtrace(char[][] board, int x, int y, Trie cur) {
        int n = board.length, m = board[0].length;
        if (cur.isEnd) {
            res.add(path.toString());
        }

        for (int[] direction : directions) {
            int i = x + direction[0], j = y + direction[1];
            if (i >= 0 && i < n && j >= 0 && j < m && ! used[i][j]) {
                char c = board[i][j];
                int index = c - 'a';
                if (cur.children[index] == null) continue;
                else {
                    used[i][j] = true;
                    path.append(c);
                    backtrace(board, i, j, cur.children[index]);
                    path.deleteCharAt(path.length() - 1);
                    used[i][j] = false;
                }
            }
        }
    }

}

class Trie {
    Trie[] children;
    boolean isEnd;
    Trie() {
        this.children = new Trie[26];
        this.isEnd = false;
    }
    void insert(String word) {
        Trie node = this;
        for (char c : word.toCharArray()) {
            int index = c - 'a';
            if (node.children[index] == null) node.children[index] = new Trie();
            node = node.children[index];
        }
        node.isEnd = true;
    }
}