LeetCode 面试经典 150_二叉搜索树_二叉搜索树的最小绝对差(85_530_C++_简单)
题目描述:
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
输入输出样例:
示例 1:
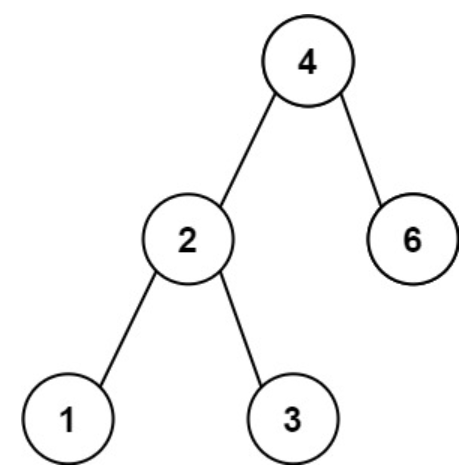
输入 :root = [4,2,6,1,3]
输出:1
示例 2:
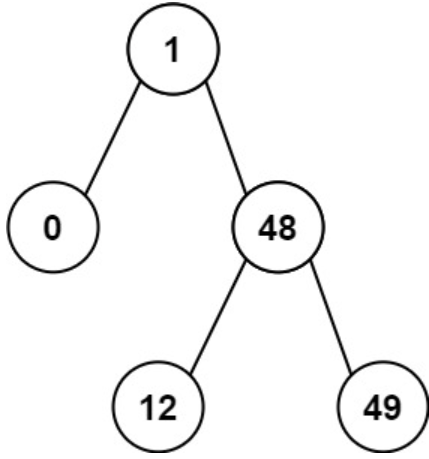
输入 :root = [1,0,48,null,null,12,49]
输出:1
提示:
树中节点的数目范围是 [2, 104]
0 <= Node.val <= 105
题解:
解题思路:
思路一(中序遍历+数组):
1、二叉搜索树 所以其中序遍历 为有序 序列。可以采用中序遍历将数据存储在数组 中,再求相邻结点的差。两结点的最小的差只能是中序遍历的相邻结点。
2、复杂度分析:
① 时间复杂度:O(n),中序遍历二叉树的每个结点O(n),遍历一遍n个元素的数组O(n)。
② 空间复杂度:O(n),递归的中序遍历二叉树为O(log n),使用数组来存储每个结点的值O(n)。
思路二(中序遍历:DFS):
1、只使用递归,不使用额外的数组。
2、复杂度分析
① 时间复杂度:O(n),结点的个数。
② 空间复杂度:O(log n),递归的深度。
代码实现
代码实现(思路一(中序遍历+数组)):
cpp
class Solution1 {
private:
vector<int> inorderNums; // 用于存储二叉树的中序遍历结果
// 中序遍历二叉树并将节点值存入inorderNums中
void inorder(TreeNode *root) {
if (root == nullptr) return; // 如果当前节点为空,返回
inorder(root->left); // 递归遍历左子树
inorderNums.push_back(root->val); // 将当前节点的值加入中序遍历结果中
inorder(root->right); // 递归遍历右子树
}
public:
// 获取二叉树中任意两个节点值的最小绝对差
int getMinimumDifference(TreeNode* root) {
inorder(root); // 通过中序遍历填充inorderNums
int ans = INT_MAX; // 初始化答案为一个最大值,后续会通过min函数更新
for (int i = 1; i < inorderNums.size(); i++) {
// 计算相邻两个节点之间的差,并更新答案为最小差值
ans = min(inorderNums[i] - inorderNums[i - 1], ans);
}
return ans; // 返回最小的差值
}
};代码实现(思路二(中序遍历:DFS)):
cpp
class Solution2 {
private:
// 中序遍历二叉树并计算相邻节点值的最小绝对差
void inorder(TreeNode *root, int &pre, int &ans) {
if (root == nullptr) return; // 如果当前节点为空,返回
inorder(root->left, pre, ans); // 递归遍历左子树
// 处理当前节点的值
if (pre == -1) {
// 这是树中的第一个节点,记录该节点值
pre = root->val;
} else {
// 计算当前节点与前一个节点的绝对差,并更新最小差值
ans = min(root->val - pre, ans);
// 更新前一个节点的值为当前节点的值
pre = root->val;
}
inorder(root->right, pre, ans); // 递归遍历右子树
}
public:
// 获取二叉树中任意两个节点值的最小绝对差
int getMinimumDifference(TreeNode* root) {
int pre = -1; // pre用于记录前一个节点的值,初始设为-1
int ans = INT_MAX; // 初始化最小差值为最大整数,表示初始时无差值
inorder(root, pre, ans); // 通过中序遍历计算最小差值
return ans; // 返回最小的绝对差值
}
};以思路二为例进行调试
cpp
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode():val(0),left(nullptr),right(nullptr){}
TreeNode(int x):val(x),left(nullptr),right(nullptr){}
TreeNode(int x,TreeNode *left,TreeNode *right):val(x),left(left),right(right){}
};
//建立二叉树,注意数组中-1为null
TreeNode *createTree(vector<int> &nums){
if (nums.empty()) return nullptr;
queue<TreeNode *> Q;
TreeNode *root=new TreeNode(nums[0]);
Q.push(root);
int i=1;
while (i<nums.size()){
TreeNode *node=Q.front();
Q.pop();
if (i<nums.size() && nums[i]!=-1){
node->left=new TreeNode(nums[i]);
Q.push(node->left);
}
i++;
if (i<nums.size() && nums[i]!=-1){
node->right=new TreeNode(nums[i]);
Q.push(node->right);
}
i++;
}
return root;
}
//中序遍历验证二叉树是否创建成功
// void inorder(TreeNode *root){
// if(root==nullptr) return;
// inorder(root->left);
// cout<<root->val<<" ";
// inorder(root->right);
// }
//方法二:只使用递归,不使用额外的数组
//时间复杂度是O(n),结点的个数
//空间复杂度是O(log n),递归的深度
class Solution2 {
private:
// 中序遍历二叉树并计算相邻节点值的最小绝对差
void inorder(TreeNode *root, int &pre, int &ans) {
if (root == nullptr) return; // 如果当前节点为空,返回
inorder(root->left, pre, ans); // 递归遍历左子树
// 处理当前节点的值
if (pre == -1) {
// 这是树中的第一个节点,记录该节点值
pre = root->val;
} else {
// 计算当前节点与前一个节点的绝对差,并更新最小差值
ans = min(root->val - pre, ans);
// 更新前一个节点的值为当前节点的值
pre = root->val;
}
inorder(root->right, pre, ans); // 递归遍历右子树
}
public:
// 获取二叉树中任意两个节点值的最小绝对差
int getMinimumDifference(TreeNode* root) {
int pre = -1; // pre用于记录前一个节点的值,初始设为-1
int ans = INT_MAX; // 初始化最小差值为最大整数,表示初始时无差值
inorder(root, pre, ans); // 通过中序遍历计算最小差值
return ans; // 返回最小的绝对差值
}
};
int main(int argc, char const *argv[])
{
vector<int> nums={4,2,6,1,3};
TreeNode* root= createTree(nums);
//验证二叉树是否创建成功
//inorder(root);
Solution2 s2;
cout<<s2.getMinimumDifference(root)<<endl;
return 0;
}LeetCode 面试经典 150_二叉搜索树_二叉搜索树的最小绝对差(85_530)原题链接
欢迎大家和我沟通交流(✿◠‿◠)