0. 前言(Introduction)
在光伏系统建模与性能评估中,光伏阵列表面辐照度(Plane of Array Irradiance, POA) 是最关键的输入之一。
POA 表示光伏组件表面实际接收到的太阳辐射总量,直接决定了组件输出功率的瞬时水平和能量产出。由于太阳辐射在空间分布上受太阳位置、大气散射、地面反射及阵列几何姿态的共同影响,因此需要对不同辐照分量进行分解与几何投影计算。
PVlib 是一个开源的光伏建模与仿真库,其 pvlib.irradiance.get_total_irradiance() 函数实现了多种经典辐照度模型(包括 Isotropic、Hay & Davies、Perez 等),可精确计算光伏阵列在任意方位与倾角下的 POA 辐照度。
本报告从 PVlib 源码出发,系统推导了 POA 直射分量、天空散射分量、地面反射分量 的计算公式,给出了完整的数学表达式、参数定义以及数值示例,从而为后续光伏输出建模和能量优化提供理论基础。
1. POA全局辐照度的定义
POA辐照度表示光伏阵列表面接收到的总太阳辐照度,由三部分组成:
- 直射分量(POA Direct):太阳直射光在阵列平面的投影。
- 天空散射分量(POA Sky Diffuse):大气散射的太阳光在阵列平面的分布。
- 地面反射分量(POA Ground Diffuse):地面反射的太阳光在阵列平面的贡献。
公式表达 :
POAglobal=POAdirect+POAsky_diffuse+POAground_diffusePOA_{global} = POA_{direct} + POA_{sky\diffuse} + POA{ground\_diffuse}POAglobal=POAdirect+POAsky_diffuse+POAground_diffuse
2. 光伏阵列表面各分量的计算公式
2.1. 直射分量(POA Direct)
直射分量是DNI(法向直射辐照度)在阵列平面上的投影,受太阳入射角(AOI)影响:
POAdirect=DNI×cos(AOI)POA_{direct} = DNI \times \cos(AOI)POAdirect=DNI×cos(AOI)
- DNI:法向直射辐照度(W/m²)。
- AOI :太阳光线与阵列平面法线的夹角(度),通过以下公式计算:
AOI=arccos[cos(β)cos(θz)+sin(β)sin(θz)cos(ϕs−ϕ)] AOI = arccos[\cos(\beta)\cos(\theta_{z}) + \sin(\beta) \sin(\theta_{z} )\cos(\phi_{s} - \phi)] AOI=arccos[cos(β)cos(θz)+sin(β)sin(θz)cos(ϕs−ϕ)]- θz\theta_{z}θz :太阳天顶角,solar_zenith。
- β\betaβ :光伏阵列倾角(度),surface_tilt。
- ϕs\phi_{s}ϕs :太阳方位角,solar_azimuth。
- ϕ\phiϕ :阵列方位角(北极为0°,南极为180°,东为90°),surface_azimuth。
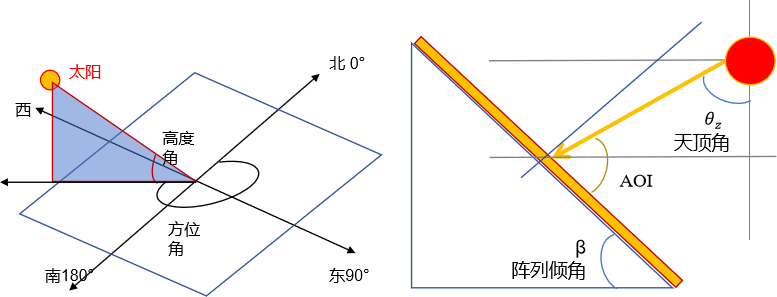
注:把 cos(AOI)cos(AOI)cos(AOI) 截断为非负 :当太阳在模块背面或入射角大于 90° 时,(cos(AOI))(\cos(AOI))(cos(AOI)) 为负,工程计算中通常用
POAdirect=DNI⋅max(cos(AOI),0)POA_{direct} = DNI \cdot \max(\cos(AOI),0)POAdirect=DNI⋅max(cos(AOI),0)同时当太阳在地平线下时也应处理 DNI=0。pvlib 的相关函数在返回投影量时需要对负值做处理(用户常把负值设为 0)
2.1. 天空散射分量(POA Sky Diffuse)
天空散射模型可选 Isotropic、Hay Davies、Perez 等,PVlib 默认支持多种模型。
2.1.1. Isotropic模型
本文天空散射分量采用Isotropic模型 计算,考虑天空亮度分布和阵列倾角:
POAsky_diffuse=DHI×1+cos(β)2POA_{\text{sky\_diffuse}} = DHI \times \frac {1 + \cos(\beta)} {2}POAsky_diffuse=DHI×21+cos(β)
- DHI:水平散射辐照度(W/m²)。
- β\betaβ : 光伏阵列的倾角。
- Isotropic模型:该模型假设天空散射均匀分布于整个半球,适用于全阴天或天空散射辐射分布均匀的场景。
参考文献:
1\] Loutzenhiser P.G. et. al. "Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation" 2007, Solar Energy vol. 81. pp. 254-267 \[2\] Hottel, H.C., Woertz, B.B., 1942. Evaluation of flat-plate solar heat collector. Trans. ASME 64, 91.
2.1.2. Hay Davies模型
天空散射分量采用Hay Davies模型计算:
POAsky_diffuse=DHI[(1−F)1+cosβ2+FRb]POA_{sky\_diffuse} = DHI\left[(1-F)\frac{1+\cos\beta}{2} + F R_b\right]POAsky_diffuse=DHI[(1−F)21+cosβ+FRb]
- Hay Davies模型:各向异性天空模型,与Isotropic模型对比,引入 Rb 项,考虑向日增强。
- 其中 (RbR_bRb) 是倾斜面与水平面直射投影比(即 ( cos(AOI)/cosθz)\cos(AOI)/\cos\theta_z )cos(AOI)/cosθz)),(FFF) 为非等向性因子(与天空清澈度相关)。
2.3. 地面反射分量(POA Ground Diffuse)
地面反射分量与地面反射率(Albedo)和光伏阵列倾角相关:
POAground_diffuse=GHI×ρ×1−cos(β)2POA_{ground\_diffuse} = GHI \times \rho \times \frac{1 - \cos(\beta)}{2} POAground_diffuse=GHI×ρ×21−cos(β)
- GHI:水平全局辐照度(W/m²)。
- ρ\rhoρ:地面反射率(默认0.2,根据地表类型调整,如雪地为0.8),Albedo。
- (1−cos(β)2)(\frac{1 - \cos(\beta)}{2})(21−cos(β)):光伏阵列倾角的几何投影因子。
参考文献:
Loutzenhiser P.G. et. al. "Empirical validation of models to compute solar irradiance on inclined surfaces for building energy simulation" 2007, Solar Energy vol. 81. pp. 254-267.
3. 最终POA Global公式
将三部分合并,得到POA全局辐照度的完整公式 :
POAglobal=DNI×cos(AOI)+DHI×1+cos(β)2+GHI×Albedo×1−cos(β)2 POA_{global} = DNI \times \cos(AOI) + DHI \times \frac {1 + \cos(\beta)} {2}+ GHI \times Albedo \times \frac{1 - \cos(\beta)}{2} POAglobal=DNI×cos(AOI)+DHI×21+cos(β)+GHI×Albedo×21−cos(β)
4. 关键参数说明
| 参数 | 单位 | 默认值 | 说明 |
|---|---|---|---|
| DNI | W/m² | - | 法向直射辐照度,需通过太阳位置算法计算 |
| DHI | W/m² | - | 水平散射辐照度 |
| GHI | W/m² | - | 水平全局辐照度 |
| β\betaβ | 度 | 用户输入 | 光伏阵列与水平面的夹角 |
| ϕ\phiϕ | 度 | 用户输入 | 阵列方位角(北为0°,东为90°,南为180°) |
| ρ\rhoρ | - | 0.25 | 地面反射率(草地0.2,雪地0.8,水面0.06) |
5. 实际应用示例
假设在正午时分:
- DNI=800W/m2DNI = 800 W/m^2DNI=800W/m2, DHI=100W/m2DHI = 100 W/m^2DHI=100W/m2, GHI=700W/m2GHI = 700 W/m^2GHI=700W/m2,
- 阵列倾角 θtilt=30∘\theta_{tilt} = 30^\circθtilt=30∘, 方位角 ϕazimuth=180∘\phi_{azimuth} = 180^\circϕazimuth=180∘(正南),
- 太阳天顶角 θzenith=30∘\theta_{zenith} = 30^\circθzenith=30∘, 太阳方位角 ϕsolar_azimuth=180∘\phi_{solar\_azimuth} = 180^\circϕsolar_azimuth=180∘,
- 地面反射率 Albedo=0.25Albedo = 0.25Albedo=0.25。
计算步骤:
-
直射分量:
- 计算AOI:
cos(AOI)=cos(30∘)cos(30∘)+sin(30∘)sin(30∘)cos(180∘−180∘)=(0.866×0.866)+(0.5×0.5×1)=0.75+0.25=1.0AOI=arccos(1.0)=0∘ \begin{aligned} \cos(AOI) &= \cos(30^\circ)\cos(30^\circ) + \sin(30^\circ)\sin(30^\circ)\cos(180^\circ - 180^\circ) \\ &= (0.866 \times 0.866) + (0.5 \times 0.5 \times 1) \\ &= 0.75 + 0.25 = 1.0 \\ AOI &= \arccos(1.0) = 0^\circ \end{aligned} cos(AOI)AOI=cos(30∘)cos(30∘)+sin(30∘)sin(30∘)cos(180∘−180∘)=(0.866×0.866)+(0.5×0.5×1)=0.75+0.25=1.0=arccos(1.0)=0∘ - 计算直射辐照度:
POAdirect=800×cos(0∘)=800×1.0=800 W/m2 POA_{\text{direct}} = 800 \times \cos(0^\circ) = 800 \times 1.0 = 800\ \text{W/m}^2 POAdirect=800×cos(0∘)=800×1.0=800 W/m2
- 计算AOI:
-
天空散射分量 :
POAsky_diffuse=100×1+cos(30∘)2=100×1+0.8662=93.3 W/m2 POA_{\text{sky\_diffuse}} = 100 \times \frac{1 + \cos(30^\circ)}{2} = 100 \times \frac{1 + 0.866}{2} = 93.3\ \text{W/m}^2 POAsky_diffuse=100×21+cos(30∘)=100×21+0.866=93.3 W/m2 -
地面反射分量 :
POAground_diffuse=700×0.25×1−cos(30∘)2=700×0.25×1−0.8662=11.7 W/m2 POA_{\text{ground\_diffuse}} = 700 \times 0.25 \times \frac{1 - \cos(30^\circ)}{2} = 700 \times 0.25 \times \frac{1 - 0.866}{2} = 11.7\ \text{W/m}^2 POAground_diffuse=700×0.25×21−cos(30∘)=700×0.25×21−0.866=11.7 W/m2 -
总POA辐照度 :
POAglobal=800+93.3+11.7=905.0 W/m2 POA_{\text{global}} = 800 + 93.3 + 11.7 = 905.0\ \text{W/m}^2 POAglobal=800+93.3+11.7=905.0 W/m2
6. 总结(Conclusion)
通过对 PVlib 源码与辐照度物理模型的分析,可以明确:光伏阵列表面接收的总辐照度(POA Global) 是由三个主要部分组成的:
- 太阳直射光在阵列平面的投影(Direct Component);
- 大气散射辐射在阵列平面的分布(Sky Diffuse Component);
- 地面反射光对阵列的附加辐射(Ground Reflected Component)。
本文采用 Isotropic 等向散射模型 对天空辐射进行近似,结合几何投影关系推导了完整的 POA 计算公式。
推导结果与 PVlib 的默认实现一致,能够较好地反映不同倾角、方位角以及太阳位置变化对阵列辐照度的影响。
在实际工程应用中,值得注意的是:
- 应根据天空条件(晴天/阴天)选择更精确的模型(如 Hay & Davies 或 Perez);
- 应在直射分量计算中处理负值截断(当太阳位于背面时);
- 并结合入射角修正(IAM)与遮挡效应,获得更接近实际功率输出的结果。
总体而言,POA 计算构成了光伏建模链条的基础环节,其精度直接影响到组件输出估算、系统设计与经济性分析的可靠性。
本文所推导的公式与计算流程可为后续的能量仿真、控制策略设计及优化分析提供清晰的理论依据与实现参考。