从傅里叶时钟到混合尺度：解构 RoPE 位置编码的演进之路

摘要

自 Transformer 架构诞生以来，位置编码一直是其核心组件之一。旋转位置编码 (RoPE) 利用傅里叶变换的"时移-相旋"特性，通过"旋转"而非"相加"的方式，将相对位置信息优雅地集成到注意力机制中，成为当今大语言模型 (LLM) 的基石。

然而，RoPE 的一个核心限制是其**"长度外推性" (Length Extrapolation) 失败**。当模型需要处理比训练时更长的序列时，其性能会急剧下降。本文将深入探讨这一问题的根源，并详细梳理从标准位置插值 (PI) 到 NTK 感知缩放 ，再到 YaRN 的完整技术演进。

我们将引入一个核心比喻------ "多频傅里叶时钟" ------来揭示为何一个看似简单的"外推"问题，需要一个"高频外推、低频内插"的精妙混合策略来解决。

1. RoPE 的核心隐喻："多频傅里叶时钟"

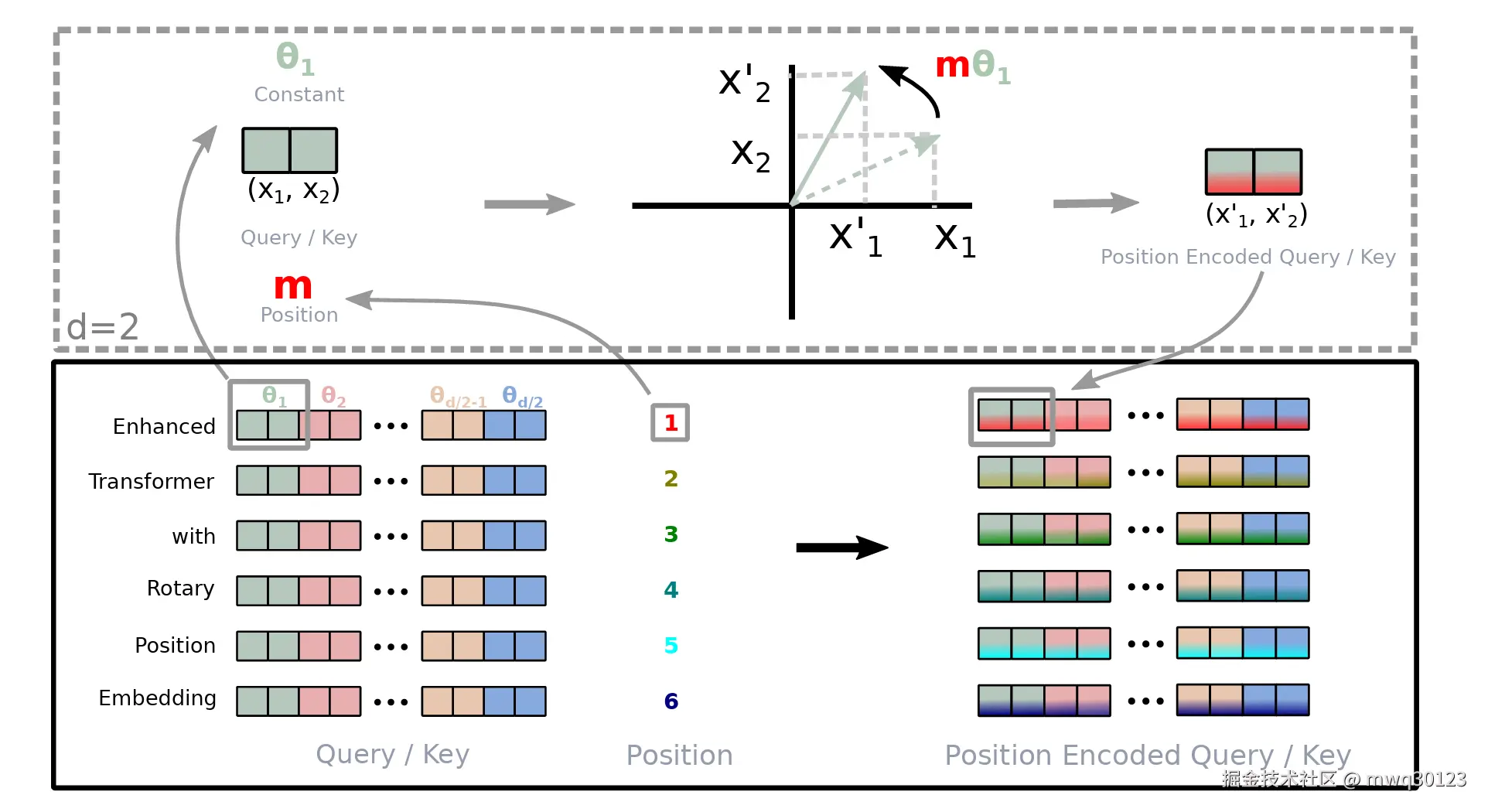
要理解 RoPE 的一切演进，我们必须首先理解它的工作原理。RoPE 将 <math xmlns="http://www.w3.org/1998/Math/MathML"> d d </math>d 维的词向量分为 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 对，每一对 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i , i + 1 ) (i, i+1) </math>(i,i+1) 都被视为一个复数（或一个 2D 向量），并根据其位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 进行旋转。

其旋转的"基准角速度"（频率）为： <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i = 1000 0 − 2 i / d \theta_i = 10000^{-2i/d} </math>θi=10000−2i/d

我们可以将这 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 对维度想象成一个**"多频傅里叶时钟"**，它有 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 根指针，每根指针 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( i ) (i) </math>(i) 都以自己不同的速度 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( θ i ) (\theta_i) </math>(θi) 转动。

1.1 高频维度："秒针" (The Second Hand)

对应： <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 值较小（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> i = 0 , 1 , . . . i=0, 1, ... </math>i=0,1,...）
特性： <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i \theta_i </math>θi 值大（接近 1），旋转极快。
作用： 在 4096 步的训练中，这根"秒针"可能已经转了成百上千圈。它不携带任何有意义的"绝对位置"信息。
模型学到了什么： 它只关心极短距离的相对位置 。例如，模型学到 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 10 m=10 </math>m=10 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 11 m=11 </math>m=11 之间，秒针旋转了（比如）90度。这个"90度"就是模型心中"相邻"的定义。
特性总结： 周期性 (Cyclical)、鲁棒 (Robust)、只关心局部相对关系。

1.2 低频维度："时针" (The Hour Hand)

对应： <math xmlns="http://www.w3.org/1998/Math/MathML"> i i </math>i 值较大（例如 <math xmlns="http://www.w3.org/1998/Math/MathML"> i = d / 2 − 1 i=d/2 - 1 </math>i=d/2−1）
特性： <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i \theta_i </math>θi 值极小（接近 0.0001），旋转极慢。
作用： 在 4096 步的训练中，这根"时针"可能只从 12:00 缓慢转到了 1:00。
模型学到了什么： 它在训练范围内是近似单调的 。模型用它来感知全局的、粗粒度的绝对位置。例如，"12:00" 意味着"文档开头"，"12:30" 意味着"中段"，"1:00" 意味着"训练过的最末尾"。
特性总结： 单调性 (Monotonic)、脆弱 (Fragile)、承载全局绝对关系。

2. 问题的出现："外推"为何会失败？

当模型在 0-4096 长度上训练后，我们让它去处理一个位于 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 5000 m=5000 </math>m=5000 的词符时：

"秒针"（高频）的反应：

它继续旋转。在 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 5000 m=5000 </math>m=5000 时，它可能指向"4:30"。这对它来说不是问题，因为在训练的几百圈里，它已经见过"4:30"无数次了。这不是"分布外"(OOD) 数据。
"时针"（低频）的反应：

它被迫从"1:00"（训练终点）继续转向"1:15"。这是灾难性的 OOD。模型在训练中从未见过"1:00"之外的角度，它的大脑"短路"了。它不知道这个"1:15"的向量代表什么，导致模型对全局位置的理解彻底崩溃。

结论： RoPE 的外推失败，根本上是低频维度的 OOD 灾难。

3. 演进一：位置插值 (PI) ------ "匀速放慢时钟"

位置插值 (Position Interpolation, PI) 是一种简单而巧妙的"作弊"手段。

思想： 我们不"外推"到 8192，而是把 0-8192 的坐标系 ，"压缩"回 0-4096 的安全区。
方法： <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = m × L t r a i n L n e w m' = m \times \frac{L_{train}}{L_{new}} </math>m′=m×LnewLtrain。例如，缩放因子 <math xmlns="http://www.w3.org/1998/Math/MathML"> s = 4096 / 8192 = 0.5 s = 4096 / 8192 = 0.5 </math>s=4096/8192=0.5。
输入： 当真实位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 8192 m=8192 </math>m=8192 时，模型计算的是 <math xmlns="http://www.w3.org/1998/Math/MathML"> R o P E ( m ′ = 4096 ) RoPE(m' = 4096) </math>RoPE(m′=4096)。当真实位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 10 m=10 </math>m=10 时，模型计算的是 <math xmlns="http://www.w3.org/1998/Math/MathML"> R o P E ( m ′ = 5 ) RoPE(m' = 5) </math>RoPE(m′=5)。
比喻： 我们把整个"傅里叶时钟"的运行速度调慢了 2 倍。

3.1 PI 的成功与"致命缺陷"

成功：

它完美解决了低频 OOD 灾难。"时针"现在在 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 8192 m=8192 </math>m=8192 时，刚好指向它熟悉的"1:00"终点，永远不会越界。
致命缺陷：

"秒针"也被迫放慢了 2 倍！
- 模型原本学到的是： <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 10 m=10 </math>m=10 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> m = 11 m=11 </math>m=11（相邻） <math xmlns="http://www.w3.org/1998/Math/MathML"> → \rightarrow </math>→ "秒针"转 90 度。
- 现在模型看到的是： <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = 5 m'=5 </math>m′=5 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = 5.5 m'=5.5 </math>m′=5.5（内插后） <math xmlns="http://www.w3.org/1998/Math/MathML"> → \rightarrow </math>→ "秒针"只转了 45 度！
- 模型对"相邻"这个最基本概念的感知被稀释和破坏了。这导致模型在局部语法、近距离依赖任务上性能急剧下降，变得"模糊"不清。

4. 演进二：NTK 感知缩放 ------ "高频外推、低频内插"的觉醒

PI 的缺陷在于它对所有频率"一刀切"。NTK (Neural Tangent Kernel) 理论启发我们：高频和低频分量在神经网络中扮演不同角色，高频对精细结构至关重要。

NTK 感知缩放 (NTK-aware Scaling) 认识到，我们不应该去压缩位置索引 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m，而应该去改变时钟的"齿轮" ，即改变基准角 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i \theta_i </math>θi。

思想： 我们希望"时针"被压缩（内插），但"秒针"保持原速（外推）。
方法：它不缩放 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m，而是去缩放旋转频率的"基座" (Base)。

原始基座 <math xmlns="http://www.w3.org/1998/Math/MathML"> b = 10000 b = 10000 </math>b=10000。 <math xmlns="http://www.w3.org/1998/Math/MathML"> θ i = b − 2 i / d \theta_i = b^{-2i/d} </math>θi=b−2i/d。

新基座 <math xmlns="http://www.w3.org/1998/Math/MathML"> b ′ = b × s ( d / ( d − 2 ) ) b' = b \times s^{(d/(d-2))} </math>b′=b×s(d/(d−2))（ <math xmlns="http://www.w3.org/1998/Math/MathML"> s s </math>s 是缩放系数）。
比喻： 我们不是"放慢时间"，而是**"更换了时钟的内部齿轮" 。通过改变基座 <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b，我们巧妙地拉平了频率谱**。其效果是：
1. 低频（时针）： 频率被大幅压缩，等效于"内插"。
2. 高频（秒针）： 频率几乎不变（或变化很小），等效于"外推"。

结论： NTK 方案是第一个在数学上实现"高频外推、低频内插"原则的方案，它通过修改频率基座 <math xmlns="http://www.w3.org/1998/Math/MathML"> b b </math>b 来代替修改位置 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m。

5. 演进三：YaRN ------ "混合动力时钟"的最终形态

NTK 方案虽然原理精妙，但仍有损失。YaRN (Yet another RoPE extension method) 采取了一种更直接、更激进、也更符合直觉的策略，它完美地实现了我们讨论的混合方案。

YaRN 结合了 PI 和 NTK 的思想，并做出了关键改进：

频率分离 (Frequency Splitting)：

YaRN 显式地将 <math xmlns="http://www.w3.org/1998/Math/MathML"> d / 2 d/2 </math>d/2 个维度分为"高频"（秒针）和"低频"（时针）。
混合插值 (Hybrid Interpolation)：
- 对于低频（时针）维度： 执行"内插" 。 <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = m × s m' = m \times s </math>m′=m×s。
- 对于高频（秒针）维度： 执行"外推" 。 <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = m m' = m </math>m′=m。
- （注：YaRN 的实现比这更平滑，它使用了一个插值函数从 <math xmlns="http://www.w3.org/1998/Math/MathML"> m m </math>m 过渡到 <math xmlns="http://www.w3.org/1998/Math/MathML"> m × s m \times s </math>m×s，但其核心思想就是区别对待）
注意力缩放 (Attention Scaling)：

YaRN 发现，当上下文变长时，注意力 logits 的方差会改变。因此，它引入了一个与缩放因子 <math xmlns="http://www.w3.org/1998/Math/MathML"> s s </math>s 相关的温度系数 <math xmlns="http://www.w3.org/1998/Math/MathML"> t t </math>t，来动态调整 Attention Softmax，防止其过于"尖锐"或"平坦"。 <math xmlns="http://www.w3.org/1998/Math/MathML"> A t t e n t i o n ( Q , K ) = Softmax ( Q K T t d k ) Attention(Q, K) = \text{Softmax}(\frac{QK^T}{t \sqrt{d_k}}) </math>Attention(Q,K)=Softmax(tdk QKT)。

YaRN 的比喻："混合动力时钟"

如果说 PI 是"匀速慢放"，NTK 是"更换齿轮"，那么 YaRN 就是一个**"混合动力时钟"**：

它告诉**"时针" ："你必须使用 内插时间**（ <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = m × s m' = m \times s </math>m′=m×s），以确保你永远在 12:00 到 1:00 的安全区内，保证全局位置感不错乱。"
它告诉**"秒针" ："你必须使用 真实时间**（ <math xmlns="http://www.w3.org/1998/Math/MathML"> m ′ = m m' = m </math>m′=m），以确保你保持原有的转速，完美保留'相邻'90度的局部感知力。"

结论

RoPE 的演进之路，是一场在"保留局部细节"与"维持全局稳定"之间不断权衡的博弈。

RoPE：利用傅里叶思想，创造了"多频时钟"。
外推失败：暴露了"时针"（低频）的 OOD 脆弱性。
PI：通过"匀速慢放"（内插）解决了 OOD，但牺牲了"秒针"（高频）的局部精度。
NTK/YaRN ：最终的领悟------我们必须区别对待：
- 用"内插"保护脆弱的低频，维持全局稳定。
- 用"外推"释放鲁棒的高频，保留局部细节。

这种"高频外推、低频内插"的混合策略，是目前 LLM 突破上下文窗口限制的最优解，它充分利用了傅里叶分解下不同频率分量的独特数学特性。