前言
🔥个人主页:不会c嘎嘎
📚专栏传送门:《数据结构》 、【C++】 、【Linux】、【算法】、【MySQL】
🐶学习方向:C++方向学习爱好者
⭐人生格言:谨言慎行,戒骄戒躁每日一鸡汤:
"别怕走得慢,只怕停下来。每一个不曾起舞的日子,都是对生命的辜负。你流下的每一滴汗水,都会在未来某个时刻开花结果。即使现在看不到希望,也要相信,黑夜再长,也挡不住黎明的光。坚持下去,不是因为看见了希望才努力,而是努力了,才能看见希望。"


1.合并区间
题目描述:
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
示例 1:
**输入:**intervals = [[1,3],[2,6],[8,10],[15,18]]
输出:[[1,6],[8,10],[15,18]]
**解释:**区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
算法原理:
这道题目需要我们先排序, 我们要按照区间的左端点(start)从小到大排序。这样排完以后,相邻两个区间只要有重叠,就一定能被发现并且连续合并(因为左端点更大的区间肯定在后面)。
核心判断:两个区间什么时候需要合并? 假设当前已经合并好的区间右端点是 currEnd,下一个区间的左端点是 nextStart: → 如果 nextStart ≤ currEnd(注意是 ≤,端点相等也要合并!),说明这两个区间有交集,必须合并。 → 合并的方式非常简单:左端点保持不变,只把右端点更新为两者更大的那个(max(currEnd, nextEnd))。 (因为已经排好序,左端点不可能变小)
具体遍历过程(以 [[1,3],[2,6],[8,10],[15,18]] 为例)先排序(本来已经有序):
初始化:currStart = 1, currEnd = 3(取第一个区间)。
1.看第2个区间 [2,6]:2 ≤ 3 → 重叠 → 把 currEnd 更新为 max(3,6)=6。现在当前合并区间变成 [1,6]。
2.看第3个区间 [8,10]:8 > 6 → 不重叠 → ① 把之前合并好的 [1,6] 加入答案数组 ② 开始新一轮合并:currStart = 8, currEnd = 10。
3.看第4个区间 [15,18]:15 > 10 → 不重叠 → ① 把 [8,10] 加入答案 ② currStart = 15, currEnd = 18。
4.遍历结束 → 别忘了把最后一个正在合并的区间 [15,18] 加入答案!这是最容易忘的一步(你已经发现了!) 循环结束后,无论最后几个区间是否发生过合并,最后一个"正在进行中的合并区间"都还没有来得及放入结果数组,所以必须在循环外再 push 一次。这也是这道题最常见的 bug 点。


时间复杂度:排序 O(n log n) + 一次遍历 O(n) → 总体 O(n log n) 空间复杂度:O(1)(不计算输出数组)
合并区间的经典解法思路:
1.先按区间的左端点从小到大排序。
2.维护当前已合并区间的"右边界" currEnd。
3.遍历每个区间:如果当前区间的左端点 ≤ currEnd → 有重叠 → 把 currEnd 更新为更大的右端点。否则 → 前面的合并结束了,把 [currStart, currEnd] 加入答案,并用当前区间开始新一轮合并。
4.遍历结束后,把最后一个合并区间加入结果
具体代码:
cpp
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
if (intervals.empty()) return {}; // 边界1:空输入
// 1. 按起点升序排序(如果起点相同,终点小的放前面更优,但不影响正确性)
sort(intervals.begin(), intervals.end());
vector<vector<int>> result;
// 用第一个区间初始化当前合并区间
int currStart = intervals[0][0];
int currEnd = intervals[0][1];
// 从第2个区间开始遍历
for (int i = 1; i < intervals.size(); ++i) {
int nextStart = intervals[i][0];
int nextEnd = intervals[i][1];
if (nextStart <= currEnd) { // 有重叠
// 合并:更新当前区间的右端点为更大的那个
currEnd = max(currEnd, nextEnd);
} else {
// 无重叠,当前合并区间结束,加入结果
result.push_back({currStart, currEnd});
// 开始新的合并区间
currStart = nextStart;
currEnd = nextEnd;
}
}
// 把最后一个合并好的区间加入结果
result.push_back({currStart, currEnd});
return result;
}
};2.连续数组
题目描述:
给定一个二进制数组 nums , 找到含有相同数量的 0 和 1 的最长连续子数组,并返回该子数组的长度。
算法原理:
核心 : 把所有 0 改成 -1 ,把所有 1 保持为 1 。 这样一来,一个子数组中 0 的个数 == 1 的个数 ⇔ 该子数组的元素和 == 0。问题转化为:求最长的子数组,其元素和为 0。
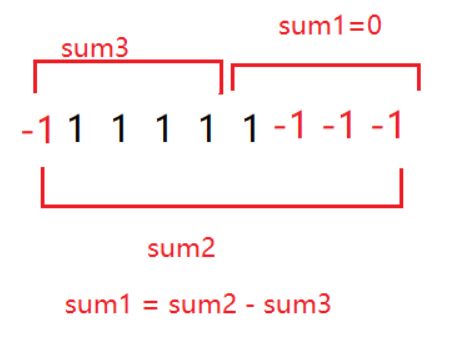
前缀和经典变形: 定义 prefix[i] 表示从头到下标 i(包含 i)的元素和(0 改 -1 后的和)。 则子数组 nums[l+1 ... r] 的和 = prefix[r] - prefix[l] 我们要它等于 0 ⇒ prefix[r] == prefix[l]。
结论:如果两个前缀和相等,那么它们之间的子数组和就是 0 → 0 和 1 数量相等!
如何用哈希表找到最长这样的最长区间?
用一个哈希表 map<前缀和, 最早出现的下标>。
初始化:map[0] = -1; (表示在下标 0 之前,前缀和为 0,这能处理从头开始的合法子数组),遍历数组,维护当前前缀和 sum。
对每个位置 i:先查表:如果 sum 已经在哈希表中出现过,说明从 map[sum]+1 到 i 这个子数组和为 0 → 用 i - map[sum] 更新答案最大值再插入/更新:只有当 sum 还没出现过时才插入! → 保证相同前缀和只记录最早的下标,这样算出来的区间才最长!
为什么必须"先查后插"? 如果你先插再查,当 sum 第一次出现时,会错误地把自己当成"之前出现过的",导致算出长度为 0 的无效区间。
为什么只保留第一次出现的下标? 因为我们追求的是最长子数组,左端点越靠左,长度越长。所以同前缀和只保留最早的那个。
具体代码:
cpp
class Solution {
public:
int findMaxLength(vector<int>& nums) {
unordered_map<int, int> firstOccur; // 前缀和 → 最早下标
firstOccur[0] = -1; // 关键初始化!
int sum = 0; // 当前前缀和(0算-1)
int ans = 0;
for (int i = 0; i < nums.size(); ++i) {
// 核心:0 → -1, 1 → 1
sum += (nums[i] == 0 ? -1 : 1);
// 先查:是否见过这个前缀和
if (firstOccur.count(sum)) {
ans = max(ans, i - firstOccur[sum]);
// 再插:只在第一次见到时插入(保证最长)
else {
firstOccur[sum] = i;
}
}
return ans;
}
};3.结语
"世界不会辜负每一个用力奔跑的人,你写下的每一行字、熬过的每一个深夜,都在悄悄为你铺就一条通往星辰的路。别怕终点遥远,只要脚步不停,终有一天,你会站在自己点亮的光里,回望来路,满眼繁花。"
以上就是本期博客的全部内容,感谢各位的阅读以及观看。如果内容有误请大佬们多多指教,一定积极改进,加以学习。
