技术背景
在分子动力学模拟所使用的分子力场中,可以大致的分为成键相互作用、非成键相互作用和多体相互作用。在上一篇文章中,我们介绍了成键相互作用力中的键能和键角能这两项,其代表的分别是两体成键相互作用和三体成键相互作用,本文主要介绍二面角项Dihedral Energy,也是四体成键相互作用中的一种(另有一种Improper Dihedral Energy,暂不在这里进行介绍)。
二面角能量项的定义
要构成一个二面角,一般需要4个原子\(i,j,k,l\)。因为二面角是力场中的成键相互作用,因此在一个二面角中至少存在这三根键:\(b_{ij},b_{jk},b_{kl}\)。我们知道,由三个不在一条直线上的点,就可以确定一个平面。在二面角中,所谓的"二面",指的是\(P_{ijk}\)和\(P_{jkl}\)这两个平面。换句话说,计算二面角,就是计算\(P_{ijk}\)和\(P_{jkl}\)这两个平面的夹角\(\psi\)。
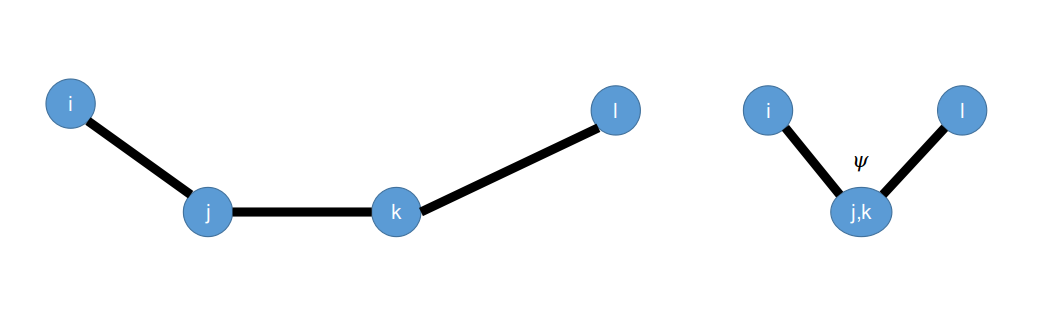
一般的计算流程就是,先计算出来平面\(P_{ijk}\)和\(P_{jkl}\)的法向量,然后求两个法向量之间的夹角\(\phi\),就可以得到两个平面之间的夹角\(\psi=\pi-\phi\)。那么,首先我们要使用\(i,j,k,l\)四个点的位置信息\(\textbf{r}_i,\textbf{r}_j,\textbf{r}k,\textbf{r}l\)去计算平面法向量\(\textbf{n}{ijk},\textbf{n}{jkl}\)。根据右手螺旋定则,我们调整一下原子序号的顺序,这样可以使得计算二面角的时候免去符号计算的问题,那么有:
\[\textbf{n}{kji}=\frac{\textbf{r}{kj}\times \textbf{r}{ji}}{\left|\textbf{r}{kj}\times \textbf{r}{ji}\right|},\textbf{n}{jkl}=\frac{\textbf{r}{jk}\times \textbf{r}{kl}}{\left|\textbf{r}{jk}\times \textbf{r}{kl}\right|} \]
然后可以计算得二面角:
\[\psi=\pi-\phi=\pi-arccos(\textbf{n}{kji}\cdot\textbf{n}{jkl}) \]
然后使用二面角势能项计算相应势能:
\[E(\psi)=k_{\psi}[1+cos(n\psi-\psi_p)] \]
其中\(n\)是一个正整数,\(k_{\psi}\)和\(\psi_p\)都是常数。当然,二面角的计算可能会有其他形式的公式,但这里我们只介绍这一种比较常用的二面角计算形式。
二面角作用力计算
二面角能量项计算之后,是要作用到每一个对应的原子上的,一共会产生四个作用力:\(\textbf{F}_i,\textbf{F}_j,\textbf{F}_k,\textbf{F}_l\),其中需要满足相互作用力之和为0的约束条件:
\[\textbf{F}_i+\textbf{F}_j+\textbf{F}_k+\textbf{F}_l=0 \]
但是需要特别说明的是,二面角作用力是力矩不守恒的,也就是二面角会使得相应的原子进行旋转操作。根据相互作用力的微分形式定义有:
\[\textbf{F}_i=-\frac{\partial E}{\partial \textbf{R}_i}=-\frac{d E}{d \psi}\frac{\partial \psi}{\partial \textbf{R}_i} \]
其中前半部分有:
\[-\frac{\partial E}{\partial \psi}=nk_{\psi}sin(n\psi-\psi_p) \]
后半部分涉及到对向量的求导,因为在\(\psi\)的计算表达式中,只有\(\textbf{n}_{kji}\)跟\(\textbf{R}_i\)有关联,因此又需要做几步链式法则(这里用到了矩阵点乘的求导法则):
\[\frac{\partial \psi}{\partial \textbf{R}i}=\frac{\partial \psi}{\partial \textbf{n}{kji}}\frac{\partial \textbf{n}{kji}}{\partial \textbf{R}i}\\ \frac{\partial \psi}{\partial \textbf{n}{kji}}=\frac{\textbf{n}{jkl}}{\sqrt{1-(\textbf{n}{kji}\cdot\textbf{n}{jkl})^2}} \]
后半部分还需要再做一次链式法则:
\[\frac{\partial \textbf{n}{kji}}{\partial \textbf{R}i}=\frac{\partial \textbf{n}{kji}}{\partial \textbf{e}{ji}}\frac{\partial\textbf{e}{ji}}{\partial\textbf{r}{ji}}\frac{\partial \textbf{r}{ji}}{\partial \textbf{R}i}=\frac{\partial \textbf{n}{kji}}{\partial \textbf{e}{ji}}\frac{\partial\textbf{e}{ji}}{\partial\textbf{r}{ji}}\textit{I} \]
最前面的这一项是一个雅克比矩阵的形式:
\[\frac{\partial \textbf{n}{kji}}{\partial \textbf{e}{ji}}=\left( \begin{matrix} 0&&z_j-z_k&&y_k-y_j\\ z_k-z_j&&0&&x_j-x_k\\ y_j-y_k&&x_k-x_j&&0 \end{matrix} \right) \]
归一化部分对应的雅克比矩阵为:
\[\frac{\partial\textbf{e}{ji}}{\partial\textbf{r}{ji}}=\left( \begin{matrix} \frac{1}{|\textbf{r}{ji}|}-\frac{x^2}{|\textbf{r}{ji}|^3}&&-\frac{xy}{|\textbf{r}{ji}|^3}&&-\frac{xz}{|\textbf{r}{ji}|^3}\\ -\frac{xy}{|\textbf{r}{ji}|^3}&&\frac{1}{|\textbf{r}{ji}|}-\frac{y^2}{|\textbf{r}{ji}|^3}&&-\frac{yz}{|\textbf{r}{ji}|^3}\\ -\frac{xz}{|\textbf{r}{ji}|^3}&&-\frac{yz}{|\textbf{r}{ji}|^3}&&\frac{1}{|\textbf{r}{ji}|}-\frac{z^2}{|\textbf{r}{ji}|^3} \end{matrix} \right)=\frac{1}{|\textbf{r}_{ji}|^3}\left( \begin{matrix} y^2+z^2&&-xy&&-xz\\ -xy&&x^2+z^2&&-yz\\ -xz&&-yz&&x^2+y^2 \end{matrix} \right) \]
整理可得:
\[\textbf{F}i=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta||\textbf{N}{kji}|}(\textbf{n}{jkl}-\textbf{n}{kji}\cos\theta)\times\textbf{r}_{kj} \]
其中
\[\textbf{N}{kji}=\textbf{r}{kj}\times\textbf{r}{ji}\\ \textbf{N}{jkl}=\textbf{r}{jk}\times\textbf{r}{kl} \]
是平面法向量的非标准化结果。那么类似的道理,可以得到原子\(l\)的作用力:
\[\textbf{F}l=-\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta||\textbf{N}{jkl}|}(\textbf{n}{kji}-\textbf{n}{jkl}\cos\theta)\times\textbf{r}_{kj} \]
比较关键的是\(j\)和\(k\)两个原子的受力,会包含多项:
\[\begin{align*} \textbf{F}j&=-\frac{\partial E}{\partial \textbf{R}j}=-\frac{\partial E}{\partial \psi}\frac{\partial\psi}{\partial\textbf{R}j}\\ &=nk\sin(n\psi-\psi_p)\left(\frac{\partial\psi}{\partial\textbf{n}{kji}}\frac{\partial\textbf{n}{kji}}{\partial\textbf{R}j}+\frac{\partial\psi}{\partial\textbf{n}{jkl}}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{R}j}\right)\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\left(\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}\frac{\partial\textbf{r}{kj}}{\partial\textbf{R}j}+\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{ji}}\frac{\partial\textbf{r}{ji}}{\partial\textbf{R}j}\right)+\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}\frac{\partial\textbf{r}{jk}}{\partial\textbf{R}{j}}\right]\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\left(\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}-\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{ji}}\right)-\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}\right]\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left(\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}-\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}\right)-\textbf{F}i\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[-\frac{1}{\left|\textbf{N}{kji}\right|}\left(\textbf{n}{jkl}-\cos\theta\textbf{n}{kji}\right)\times\textbf{r}{ji}+\frac{1}{\left|\textbf{N}{jkl}\right|}\left(\textbf{n}{kji}-\cos\theta\textbf{n}{jkl}\right)\times\textbf{r}{kl}\right]-\textbf{F}_i \end{align*} \]
此处用到一个化简,如果有\(\textbf{r}=\textbf{r}_1\times\textbf{r}_2\),则:
\[\textbf{e}\frac{\partial\textbf{r}}{\partial\textbf{r}_1}=-\textbf{e}\times\textbf{r}_2\\ \textbf{e}\frac{\partial\textbf{r}}{\partial\textbf{r}_2}=\textbf{e}\times\textbf{r}_1 \]
那么使用类似的方法也可以计算得原子\(k\)上的作用力:
\[\begin{align*} \textbf{F}k&=\frac{\partial E}{\partial \textbf{R}k}=-\frac{\partial E}{\partial\psi}\frac{\partial\psi}{\partial\textbf{R}k}\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}\frac{\partial\textbf{r}{kj}}{\partial\textbf{R}k}+\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\left(\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}\frac{\partial\textbf{r}{jk}}{\partial\textbf{R}{k}}+\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{kl}}\frac{\partial\textbf{r}{kl}}{\partial\textbf{R}{k}}\right)\right]\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[-\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}+\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\left(\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}-\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{kl}}\right)\right]\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left(\textbf{n}{kji}\frac{\partial\textbf{n}{jkl}}{\partial\textbf{N}{jkl}}\frac{\partial\textbf{N}{jkl}}{\partial\textbf{r}{jk}}-\textbf{n}{jkl}\frac{\partial\textbf{n}{kji}}{\partial\textbf{N}{kji}}\frac{\partial\textbf{N}{kji}}{\partial\textbf{r}{kj}}\right)-\textbf{F}l\\ &=\frac{nk\sin(n\psi-\psi_p)}{|\sin\theta|}\left[-\frac{1}{|\textbf{N}{jkl}|}(\textbf{n}{kji}-\cos\theta\textbf{n}{jkl})\times\textbf{r}{kl}+\frac{1}{|\textbf{N}{kji}|}(\textbf{n}{jkl}-\cos\theta\textbf{n}{kji})\times\textbf{n}{ji}\right]-\textbf{F}_l \end{align*} \]
那么到这里为止,我们就得到了所有的二面角的四个顶点原子的作用力。
总结概要
接前面一篇关于键长和键角的相互作用力计算的文章,本文简单的计算了一下传统分子力场项中常见的二面角项的相互作用力。
版权声明
本文首发链接为:https://www.cnblogs.com/dechinphy/p/dihedral-1.html
作者ID:DechinPhy
更多原著文章:https://www.cnblogs.com/dechinphy/
请博主喝咖啡:https://www.cnblogs.com/dechinphy/gallery/image/379634.html