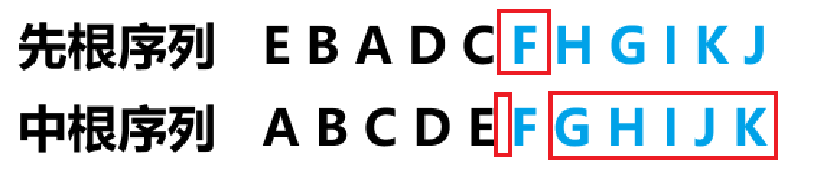1.二叉树遍历方式
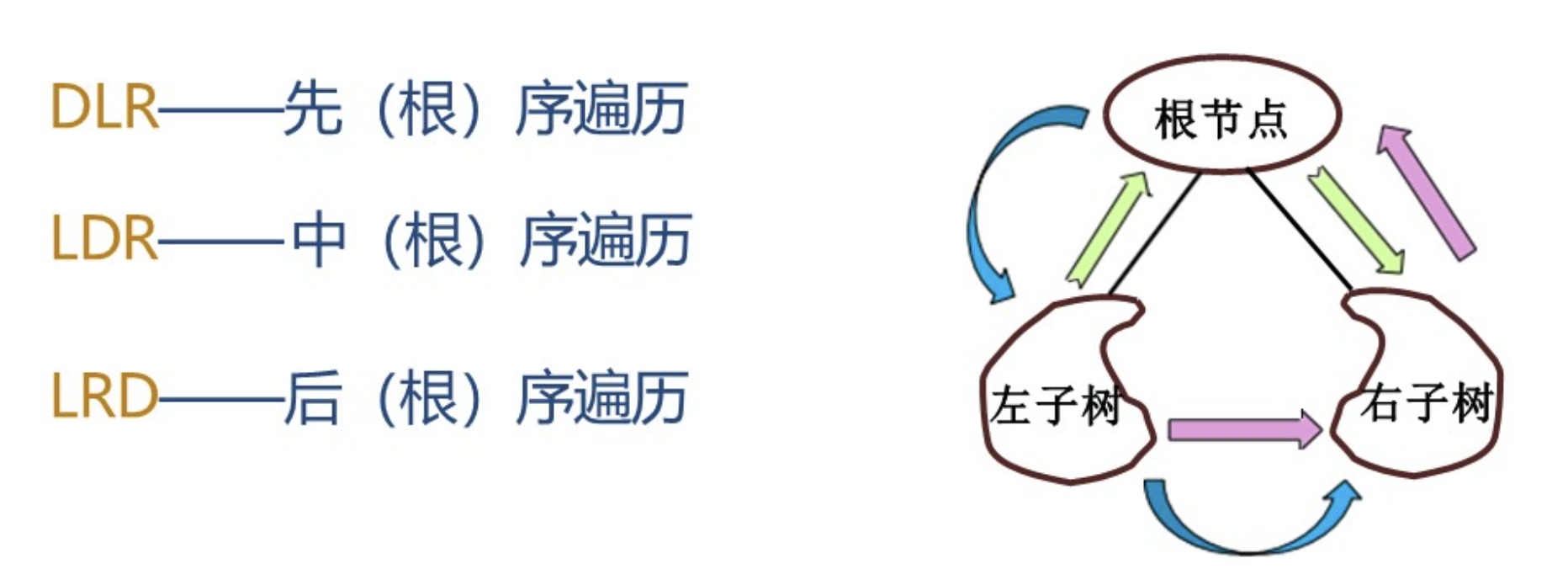
1.1 先序遍历
- 访问根节点
- 先序遍历左子树
- 先序遍历右子树
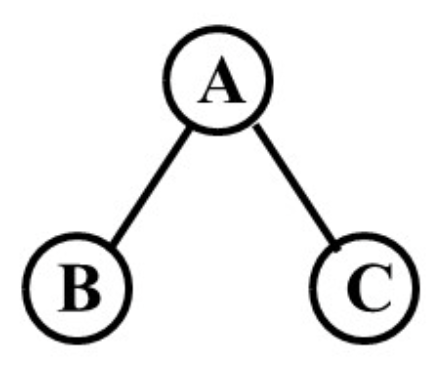
图中遍历顺序为A,B,C
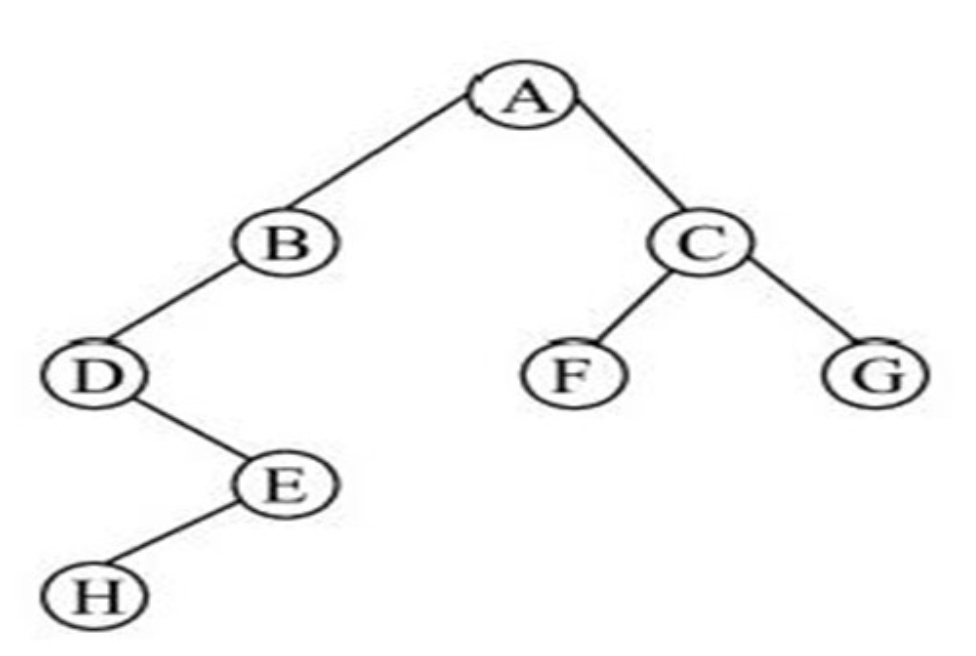
- 按照先序遍历思想,先访问根结点,再访问左子树,最后访问右子树,即根左右的顺序。
- 该二叉树的根结点为 A 结点,则 A 结点先被访问,继续访问 A 结点的左子树。
- A 结点左子树依然先访问根结点 B,然后继续递归访问 B 结点的左子树,访问 B 结点的左子树根结点 D,继续访问 D 结点的左子树,左子树为空,继续访问 D 结点右子树,访问完其根结点 E 后继续访问 E 的左子树,左子树根结点为 H 结点。至此,以 A 结点为根的左子树全部访问完毕。
- 继续访问该二叉树右子树。首先访问根结点 C,继续访问其左子树根结点 F,至此,A 子树结点访问完毕,继续访问右子树根结点 G。
- 可得二叉树的先(前)序遍历序列为 A、B、D、E、H、C、F、G。
1.2 中序遍历
- 中序遍历左子树
- 访问根节点
- 中序遍历右子树
图中遍历顺序为B,A,C

- 按照中序遍历思想,先访问左子树,再访问根、结点,最后访问右子树,即左根右的顺序。
- 从根结点向左下方寻找,直到某一结点没有左子树为止。
- 因 D 结点左子树为空,则访问它自身,而后继续访问 D 结点的右子树。
- 其右子树中也是顺着左下方寻找,发现 H 结点不再有左子树,故 D 结点的左子树中先访问 H 结点,继续访问 H 所在子树的根结点,即 B 结点。B 结点右孩子为空,至此,以 A 结点为根的左子树全部访问完毕。
- 继续访问根结点 A,再访问其右子树。右子树中还是向左下方寻找,F 结点没有左孩子,则先访问它,再访问 F 所在子树的根结点 C,后访问 C 的右孩子。
- C 右孩子的左子树为空,再先访问右孩子的根结点 G,G 结点的右孩子为空,则该树访问完毕。
- 故可得二叉树的中序遍历序列为 D、H、E、B、A、F、C、G。
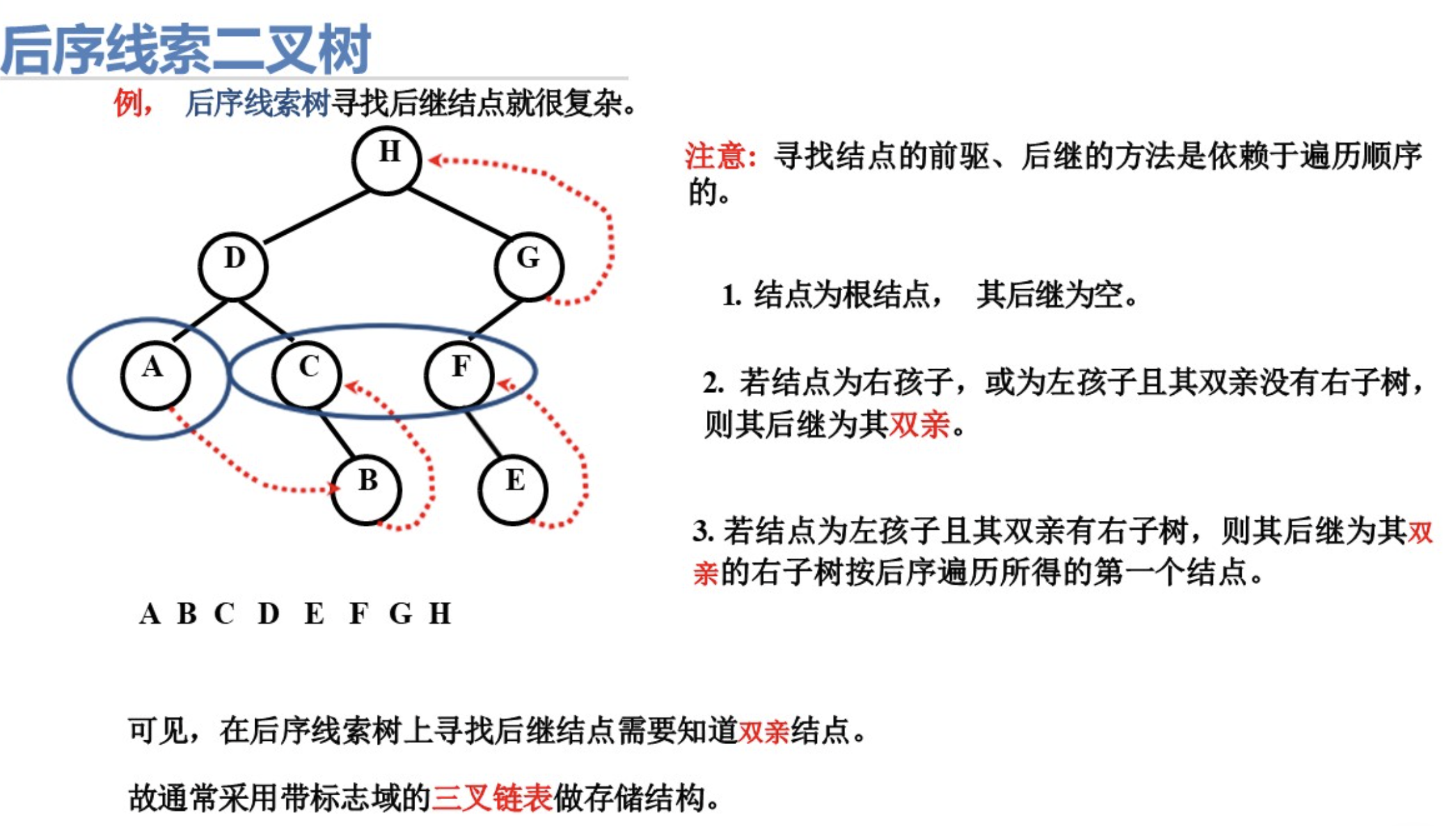
1.3 后序遍历
- 后序遍历左子树
- 后序遍历右子树
- 访问根节点
图中遍历顺序为B,C,A

- 按照后序遍历思想,先访问左子树,再访问右子树,最后访问根结点,即左右根的顺序。
- 从根结点向左下方寻找,直到某一结点没有左子树为止。
- 因 D 结点左子树为空,再访问其右子树,右子树中依旧先访问其左子树;结点 H 不再有左子树,故先访问它,再访问以 E 结点为根的右子树,B 结点的右子树为空,则访问它本身。后访问 E 结点的根结点 D,再访问 D 的根结点 B 结点。
- 至此,A 结点的左子树访问完毕。继续访问 A 结点的右子树。沿着右子树的左下方访问,C 结点的左孩子 F 结点没有左孩子,则访问它。后访问 C 结点的右子树。
- G 结点左右孩子为空,则访问 G 结点。至此,C 结点的左右子树均访问完毕,继续访问 C 结点。A 的右子树也访问完毕,最后访问根结点 A。
- 故可得二叉树的后序遍历序列为H、E、D、B、F、G、C、A。
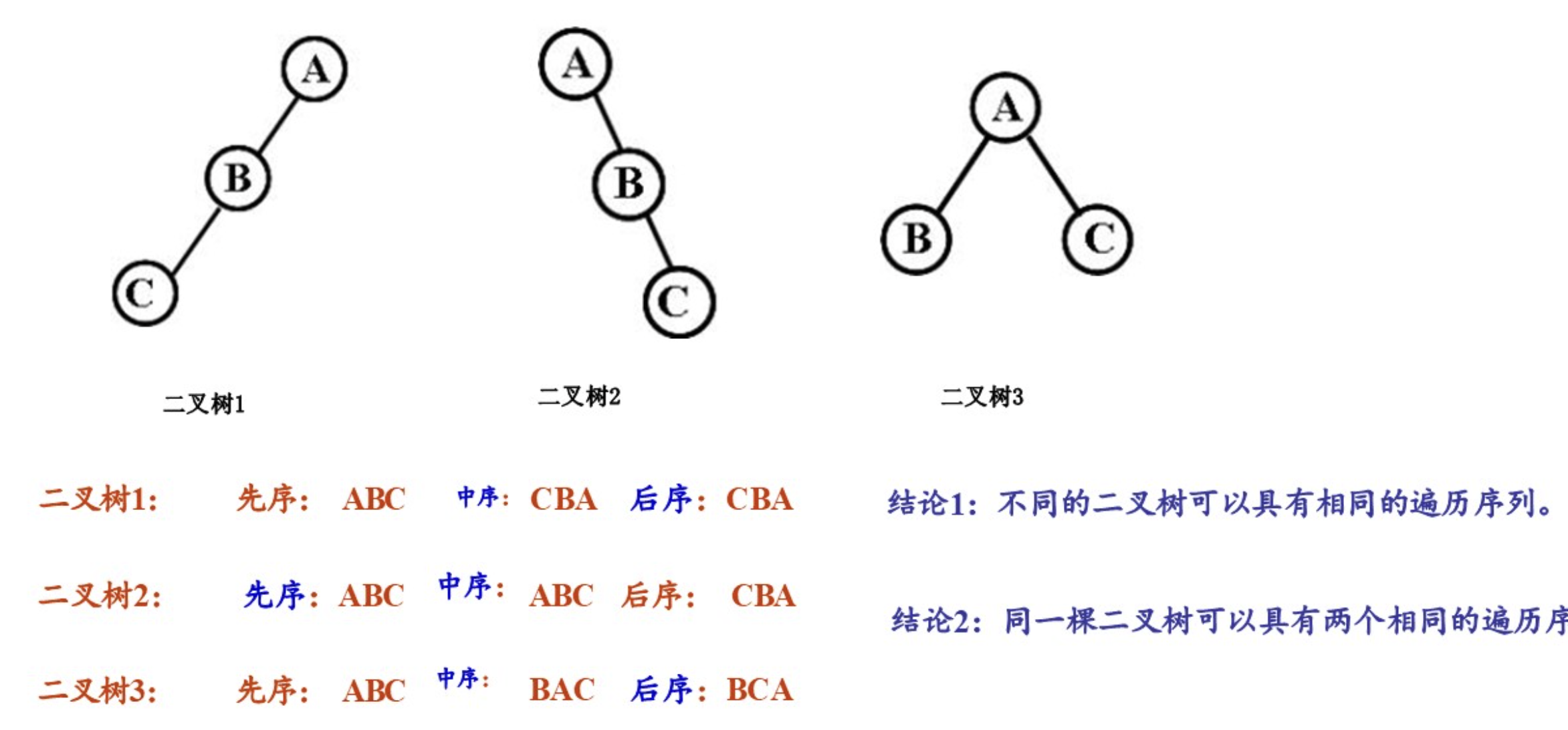
2.例题练习
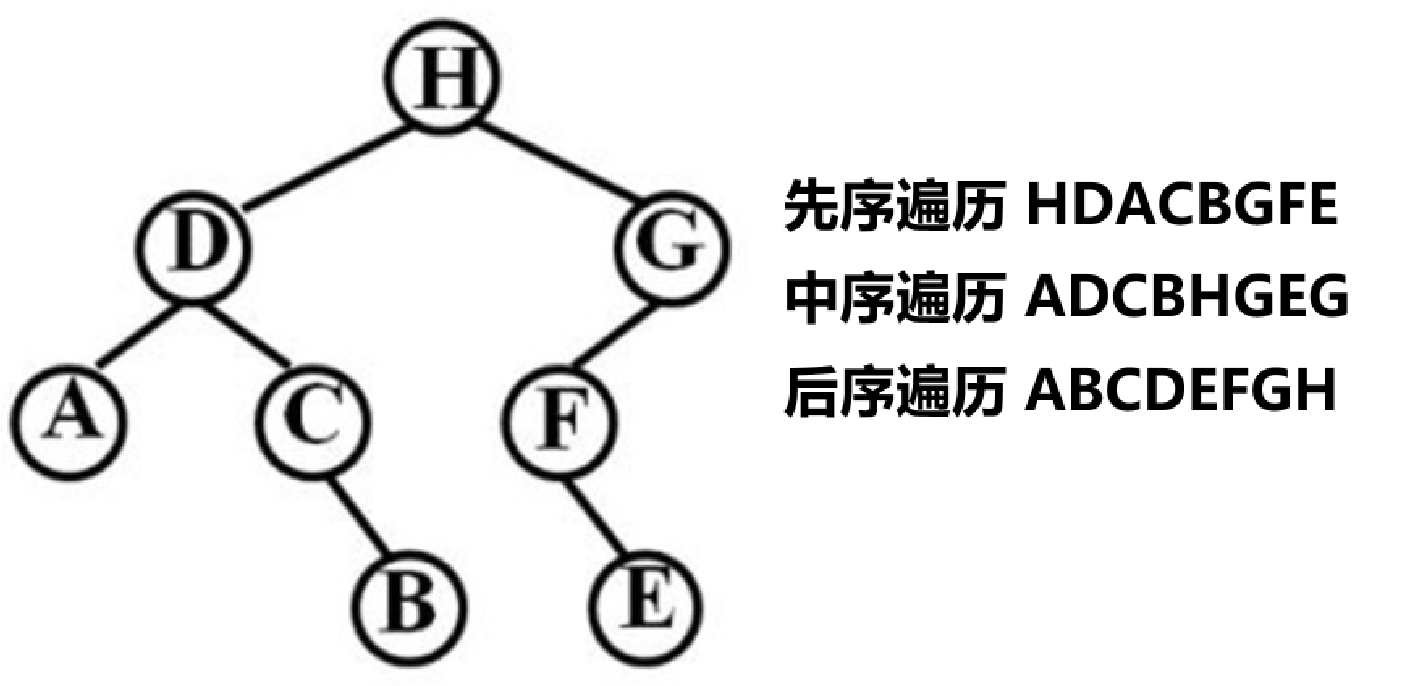
3.由遍历序列构造二叉树
先序确定根(开头元素),中序分左右
后序确定根(末尾元素),中序分左右
3.1 先序与中序序列
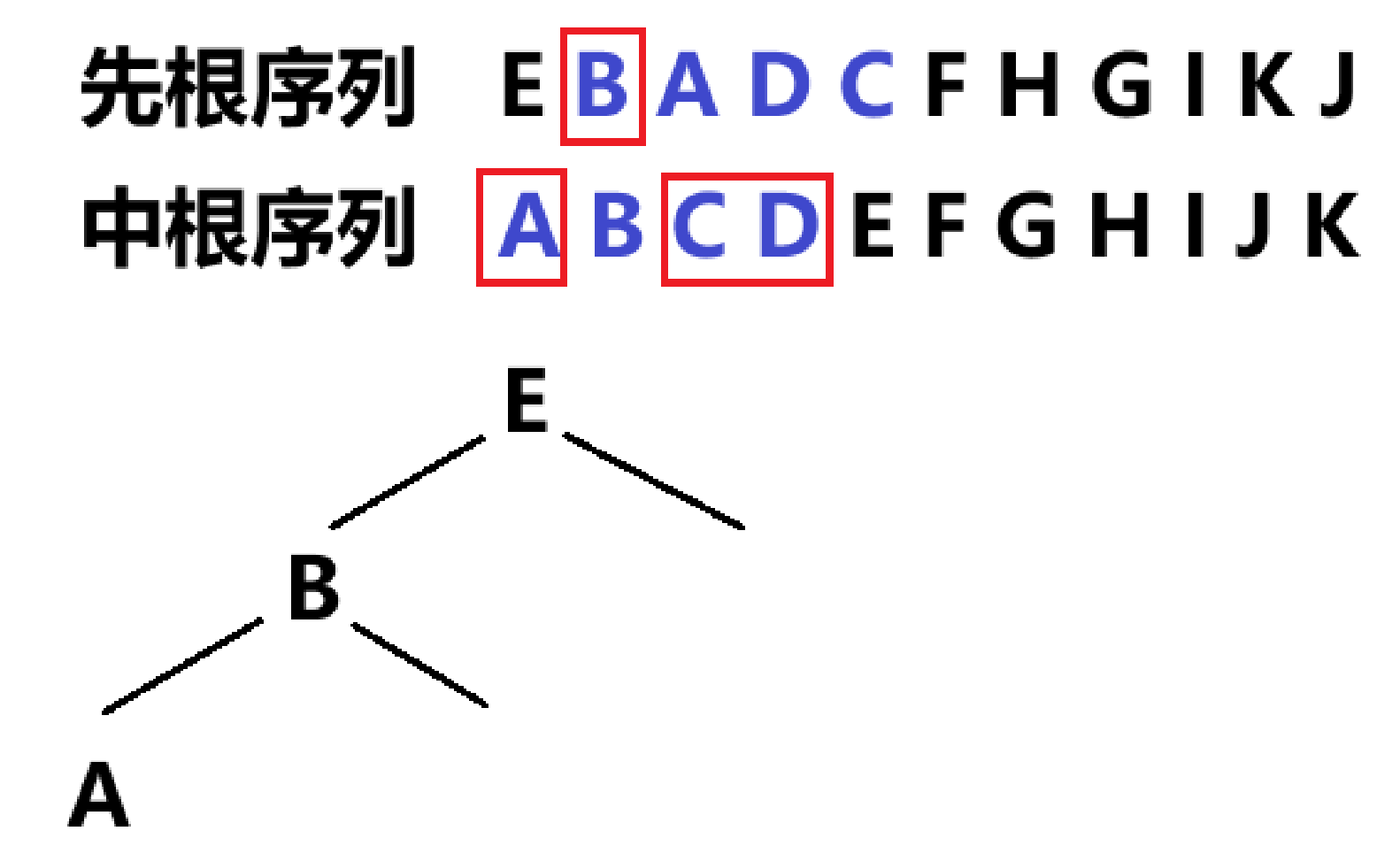
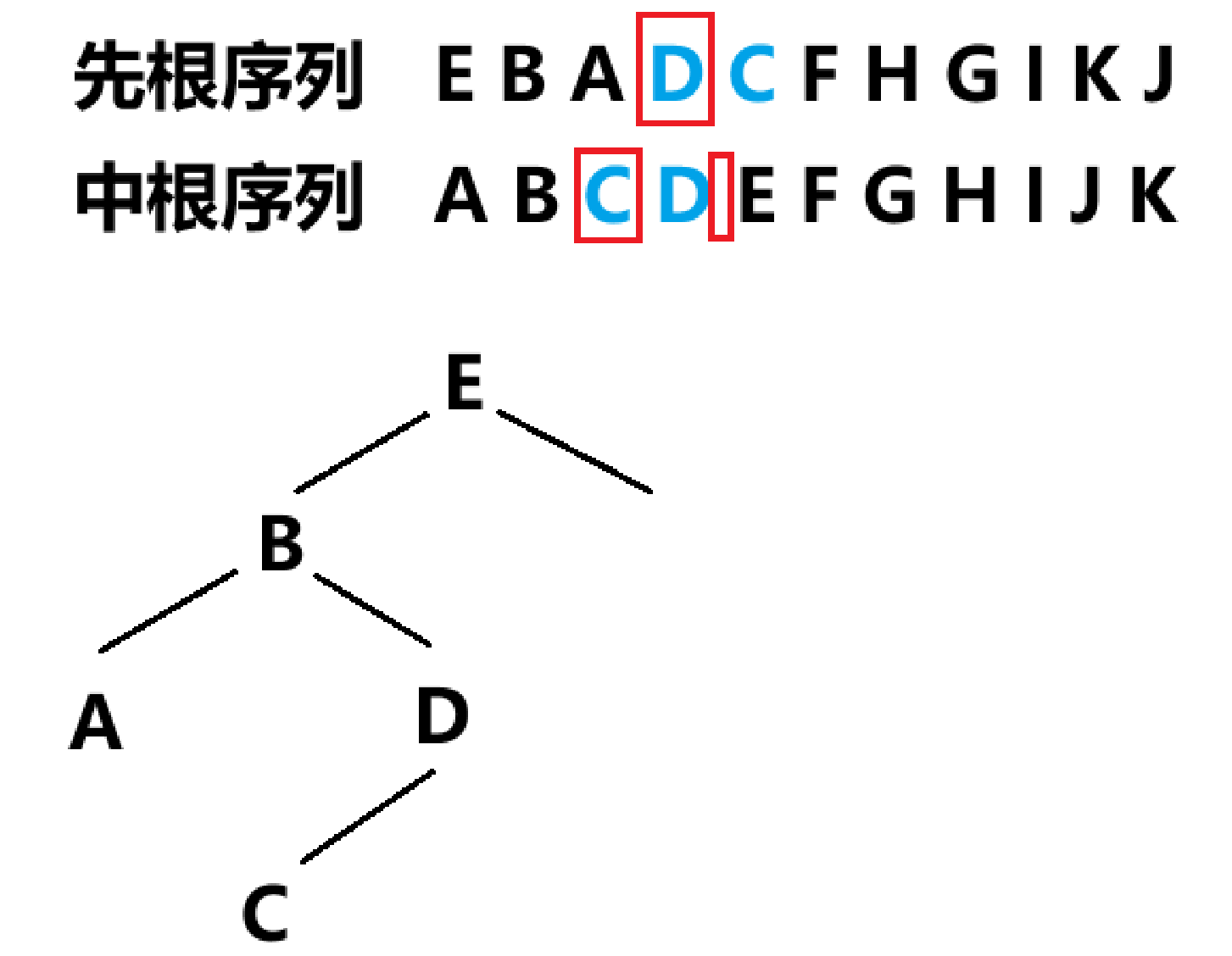
已知一棵二叉树的先根序列为EBADCFHGIKJ ,中根序列为 ABCDEFGHIJK试画出这棵二叉树。
- 在先根序列中找到头元素E,在中根序列中以E为中心分割
- 在先根序列中对应找到 BADC,B在首位,则B为左子树的头元素
- 回归到中根序列,元素B将ABCD分割成A与CD两部分,对应左右子树
- 单独对右子树CD进行分析,在先根序列中对应找到 DC,D为头元素
- 回归到回归到中根序列,元素D左侧为C,右侧为空
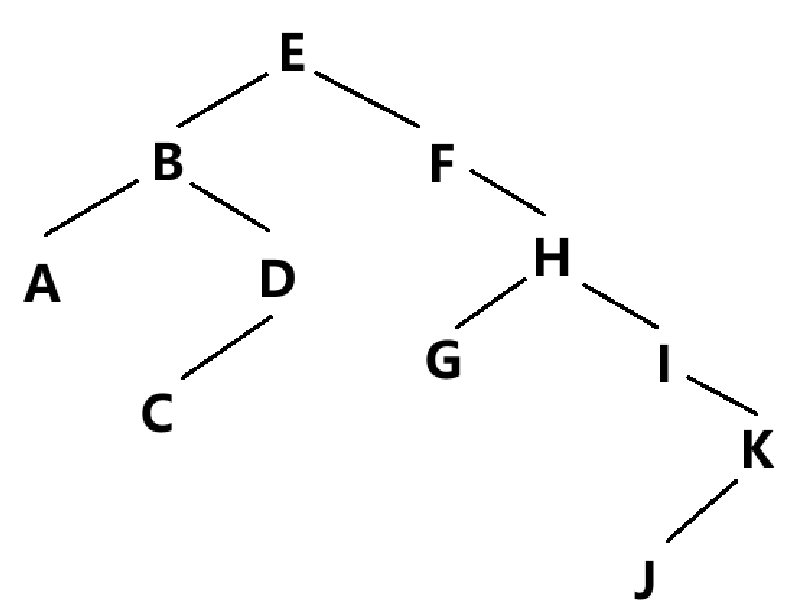
- 同理,运用以上方法对右子树进行分析,在先根序列中确定头元素,在中根序列中区分左右子树,依次循环往复
最终得到完整的二叉树,如图所示
3.2 后序与中序序列
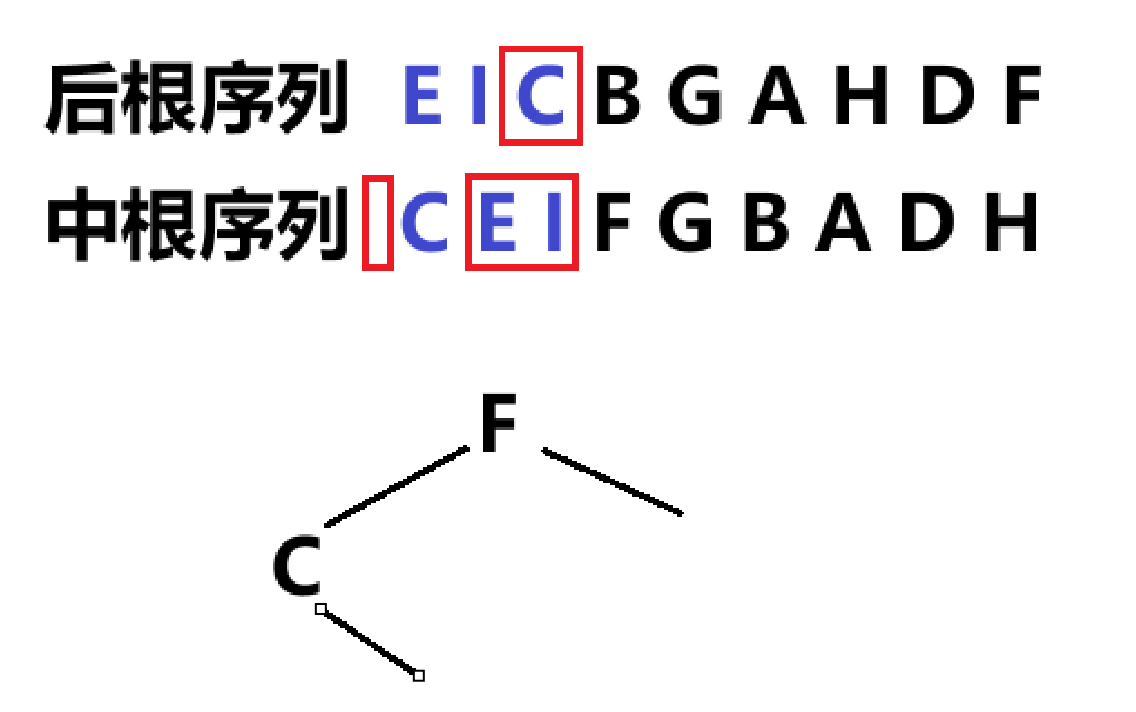
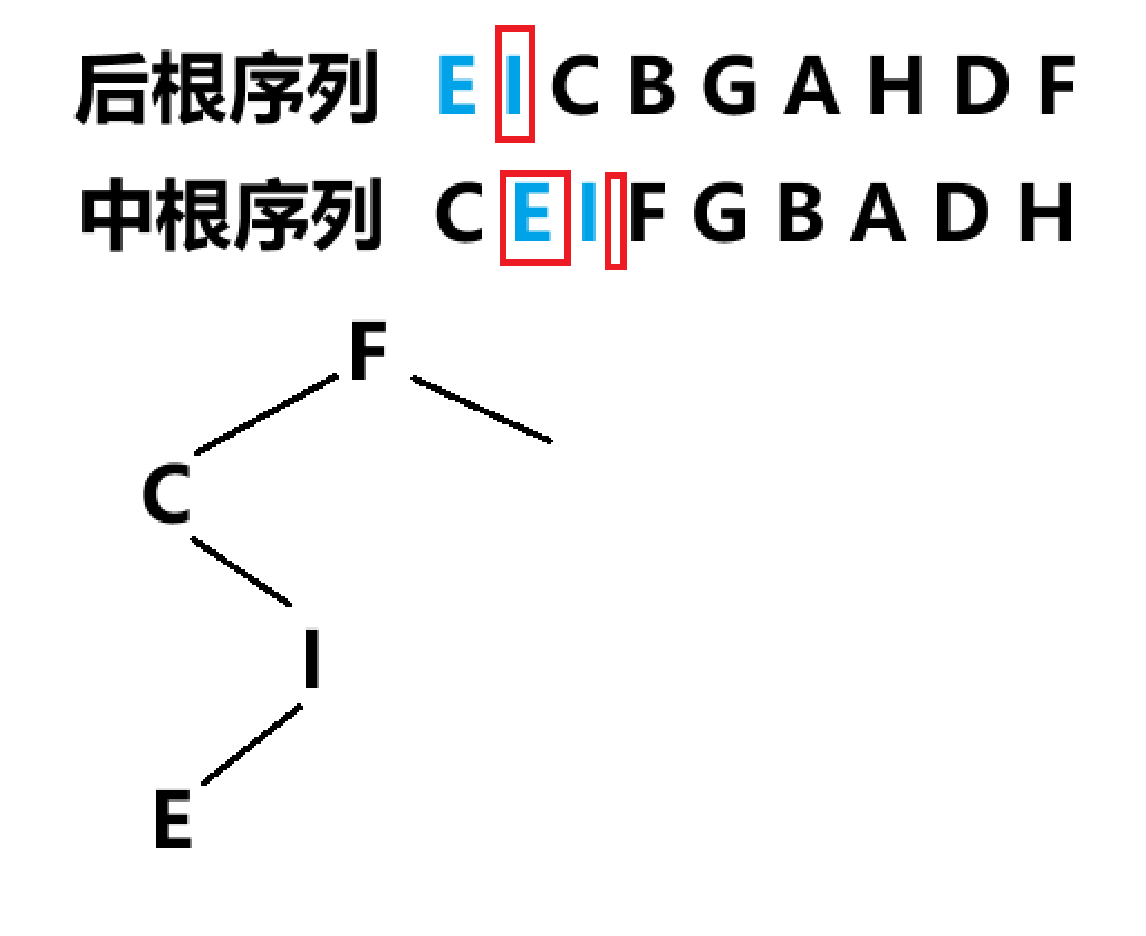
已知一棵二叉树的后根遍历序列为 EICBGAHDF ,同时知道该二叉树的中根遍历序列为CEIFGBADH,试画出该二叉树
后根遍历序列中,头元素位于末端
- 根据后根序列,找到头元素F,在中根序列中分割成CEI与GBADH两部分
- 单独定位CEI进行分析,由后根序列可知C为头元素
- 回归到中根序列,C左子树为空,右子树为EI
- 单独定位EI,由后根序列可知I为头元素
- 回归到中根序列,I左子树为E,右子树为空
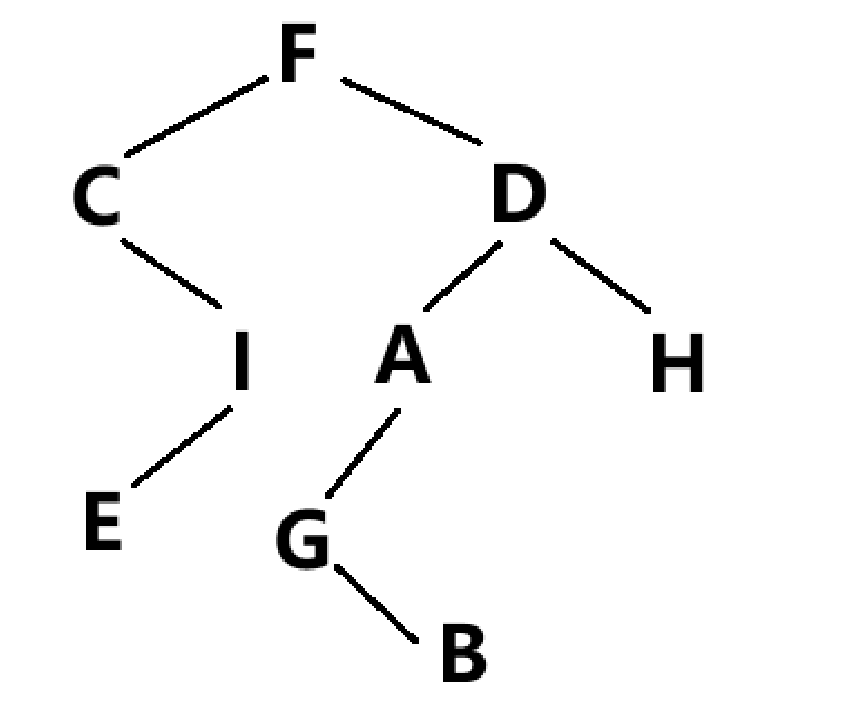
- 同理,运用以上方法对右子树进行分析,在后根序列中确定头元素,在中根序列中区分左右子树,依次循环往复,最终二叉树如图所示
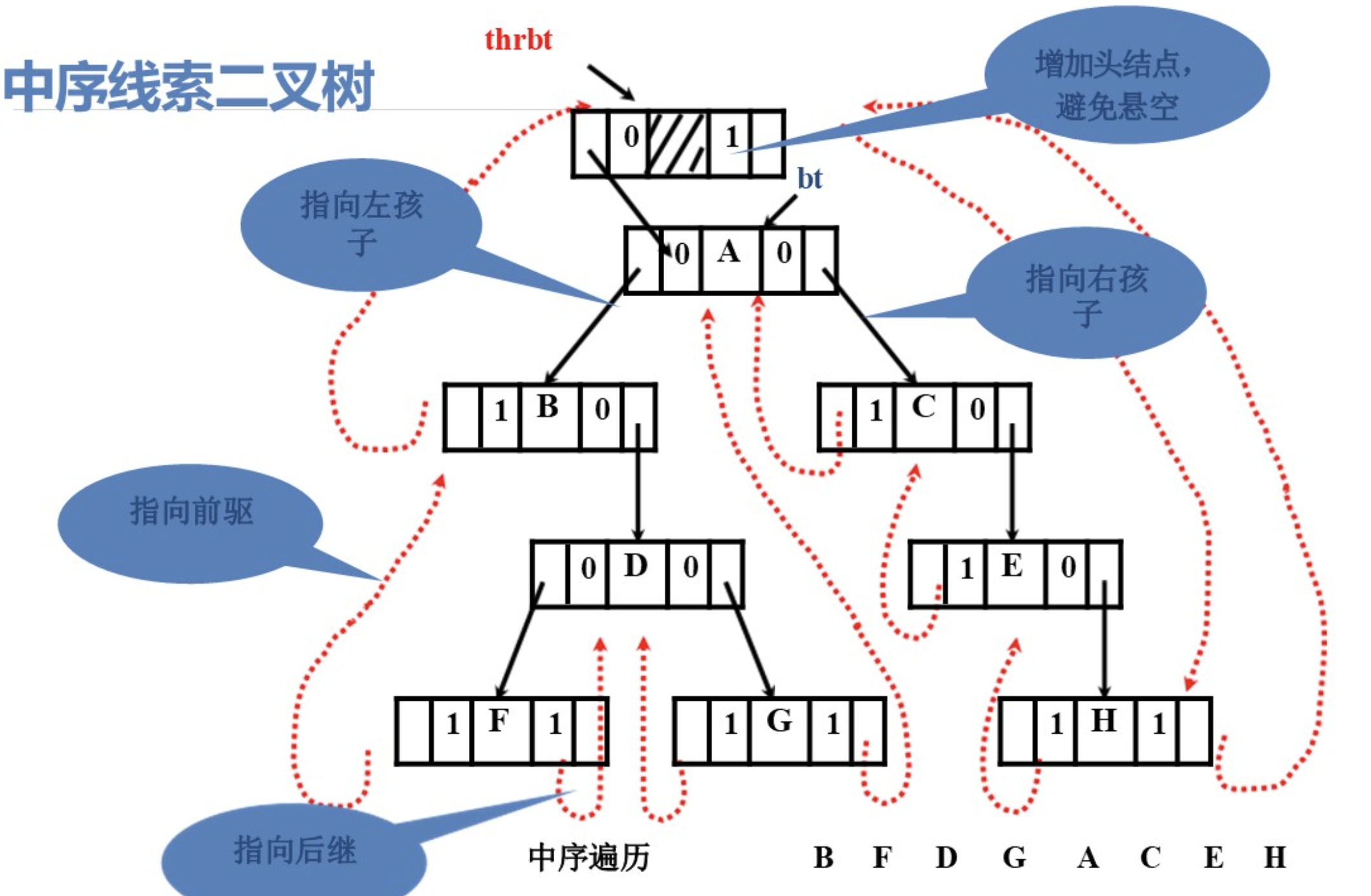
4.线索二叉树
4.1 概念定义
在普通二叉树中,存在大量空指针 (叶子节点的左右指针为空,非叶子节点的某侧子树为空时也会有空指针)。线索二叉树通过利用这些空指针存储遍历序列的前驱或后继节点信息,将二叉树 "线索化",从而实现高效的遍历(无需递归或栈,直接通过线索找到前驱 / 后继)。
二叉树的遍历实现了对一个非线性结构进行线性化的操作,从而使每个结点在线性序列中有且仅有一个直接前驱和直接后继。
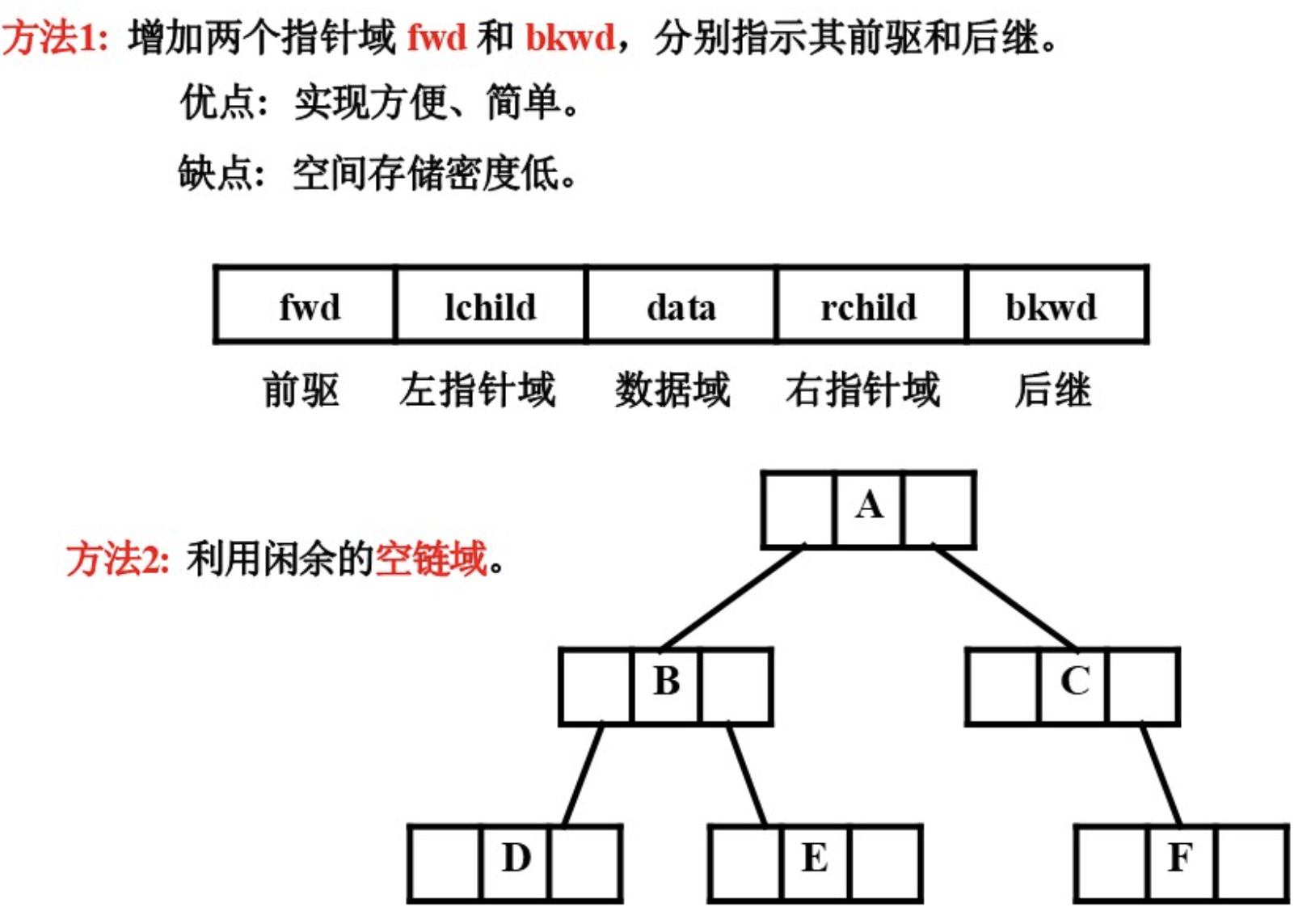
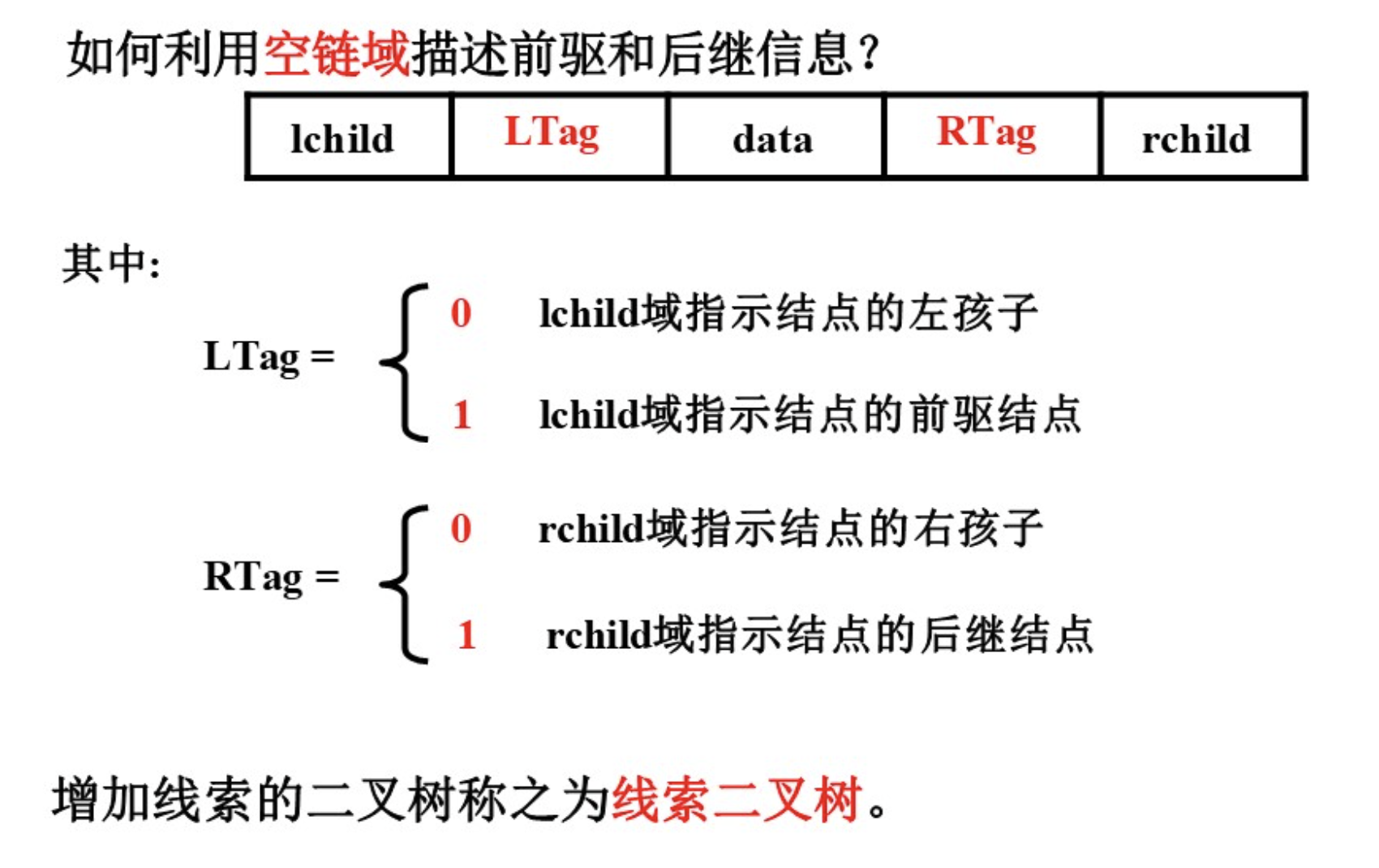
4.2 线索二叉树画法
先写出中序遍历序列,根据前驱与后继画图