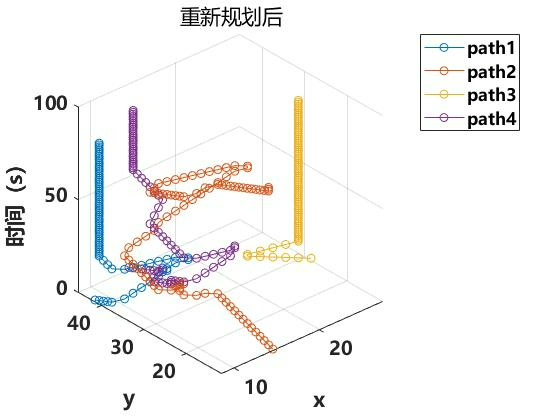
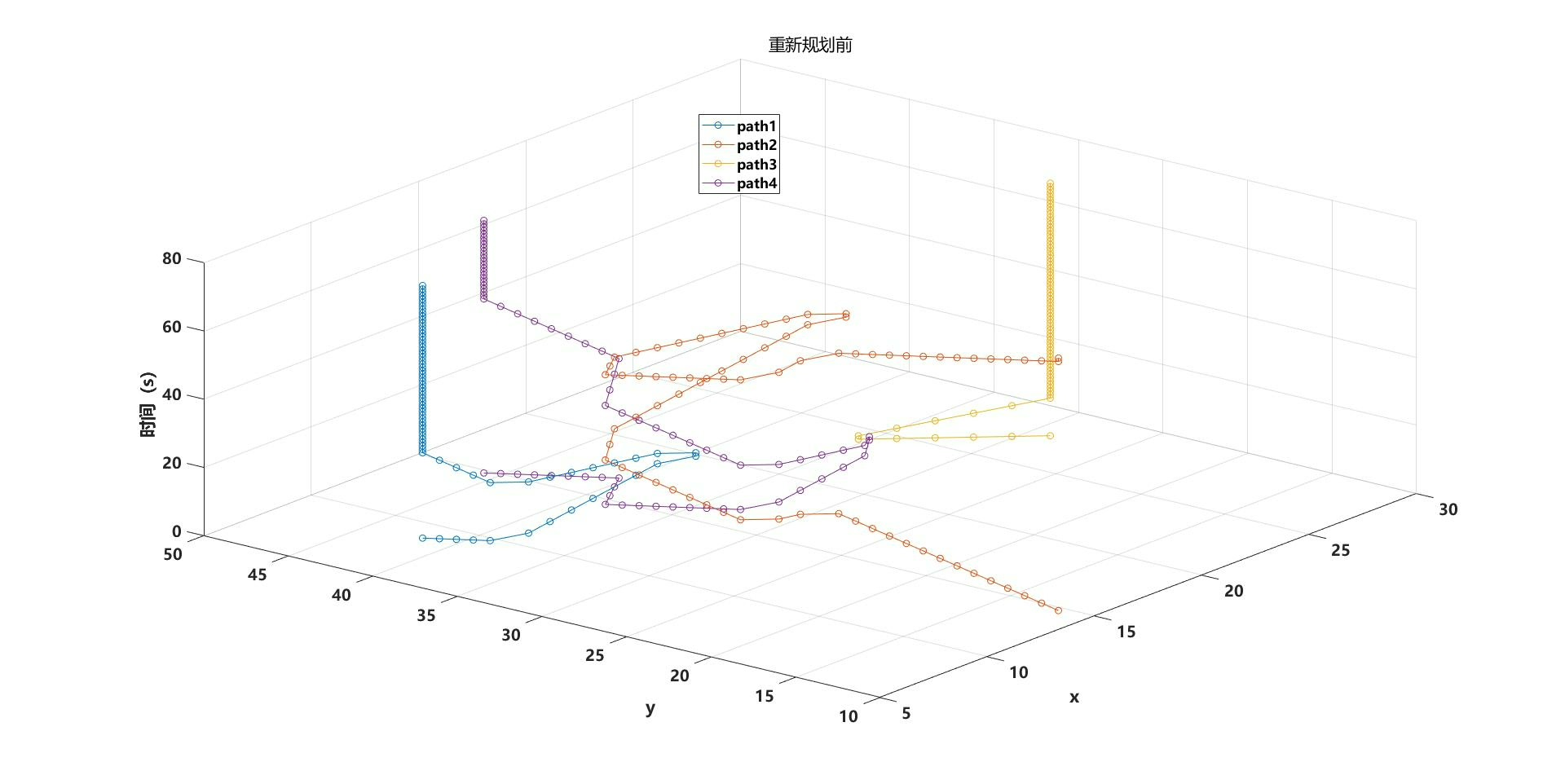
使用Matlab基于A星算法的多任务多AGV路径规划系统优化

使用matlab基于a星算法的多任务多AGV路径规划系统优化，环境是一个仓库，多个agv可以自由移动，考虑到通道占用问题，使用路径规划方法实现避障及最短路规划。关键词:多任务多agv 避障

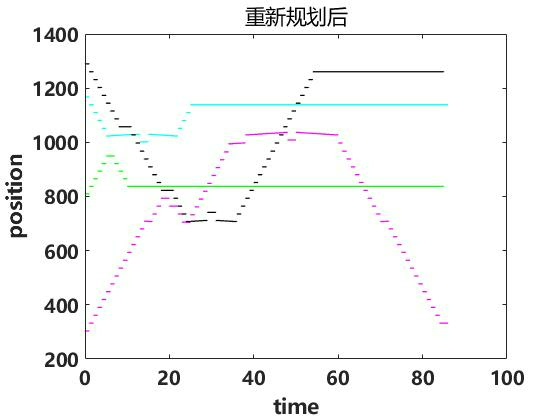
在现代化的仓储物流场景中，多AGV（自动导引车）协同完成多任务的情况越来越常见。为了提升效率并避免冲突，基于A星算法的路径规划系统优化就显得尤为重要。今天咱们就来聊聊在Matlab环境下，针对仓库场景，如何实现这个优化。

仓库环境建模

仓库环境可以看作是一个二维的网格地图。我们可以用一个矩阵来表示这个地图，矩阵中的每个元素代表地图中的一个网格单元。0表示可通行区域，1表示障碍物区域。比如：

matlab 复制代码

% 创建一个简单的仓库地图示例
warehouseMap = [0 0 0 0 0;
                0 1 0 1 0;
                0 0 0 0 0;
                0 1 0 1 0;
                0 0 0 0 0];

这里我们构建了一个5x5的简单仓库地图，其中1所在位置就是障碍物。

A星算法核心原理与代码实现

A星算法是一种启发式搜索算法，用于在加权图中寻找从起始节点到目标节点的最短路径。它结合了Dijkstra算法的广度优先搜索策略和最佳优先搜索策略。其核心思想是通过评估函数 f(n) = g(n) + h(n) 来选择下一个要扩展的节点，其中 g(n) 是从起点到节点 n 的实际代价，h(n) 是从节点 n 到目标节点的估计代价。

matlab 复制代码

function [path, cost] = aStarSearch(map, start, goal)
    % 初始化
    openSet = [start];
    cameFrom = containers.Map;
    gScore = containers.Map(num2cell(start), 0);
    fScore = containers.Map(num2cell(start), heuristic(start, goal));

    while ~isempty(openSet)
        % 找到fScore最小的节点
        [~, bestIndex] = min([fScore.values{:}]);
        current = openSet(bestIndex);
        openSet(bestIndex) = [];

        if isequal(current, goal)
            % 找到路径，回溯
            path = reconstructPath(cameFrom, current);
            cost = gScore(num2cell(current));
            return;
        end

        % 扩展当前节点
        neighbors = getNeighbors(current, map);
        for i = 1:size(neighbors, 1)
            neighbor = neighbors(i, :);
            tentativeGScore = gScore(num2cell(current)) + 1;

            if ~gScore.isKey(num2cell(neighbor)) || tentativeGScore < gScore(num2cell(neighbor))
                cameFrom(num2cell(neighbor)) = current;
                gScore(num2cell(neighbor)) = tentativeGScore;
                fScore(num2cell(neighbor)) = tentativeGScore + heuristic(neighbor, goal);
                if ~ismember(neighbor, openSet, 'rows')
                    openSet = [openSet; neighbor];
                end
            end
        end
    end

    % 没有找到路径
    path = [];
    cost = Inf;
end

function h = heuristic(node, goal)
    % 曼哈顿距离作为启发函数
    h = abs(node(1) - goal(1)) + abs(node(2) - goal(2));
end

function neighbors = getNeighbors(node, map)
    % 获取邻居节点
    neighbors = [];
    rows = size(map, 1);
    cols = size(map, 2);
    for i = -1:1
        for j = -1:1
            if ~(i == 0 && j == 0)
                neighbor = node + [i j];
                if neighbor(1) >= 1 && neighbor(1) <= rows && neighbor(2) >= 1 && neighbor(2) <= cols && map(neighbor(1), neighbor(2)) == 0
                    neighbors = [neighbors; neighbor];
                end
            end
        end
    end
end

function path = reconstructPath(cameFrom, current)
    % 回溯路径
    path = current;
    while cameFrom.isKey(num2cell(current))
        current = cameFrom(num2cell(current));
        path = [current; path];
    end
end

上述代码实现了A星算法的核心部分。aStarSearch 函数实现了整个搜索流程，heuristic 函数定义了启发式函数（这里使用曼哈顿距离），getNeighbors 函数用于获取当前节点的邻居节点，reconstructPath 函数则是在找到目标节点后回溯路径。

多AGV路径规划与避障

对于多AGV系统，我们不仅要为每个AGV规划路径，还要考虑通道占用和避障问题。一种简单的方法是为每个AGV依次规划路径，并在规划过程中，将已规划路径上的节点标记为临时障碍物，避免后续AGV重复经过。

matlab 复制代码

% 假设多个AGV的起点和终点
startPoints = [[1, 1]; [1, 5]];
goalPoints = [[5, 5]; [5, 1]];
numAGVs = size(startPoints, 1);
map = warehouseMap;

for k = 1:numAGVs
    [path, ~] = aStarSearch(map, startPoints(k, :), goalPoints(k, :));
    if ~isempty(path)
        % 将路径上的点标记为临时障碍物，避免其他AGV走
        for i = 1:size(path, 1)
            map(path(i, 1), path(i, 2)) = 1;
        end
    end
end

这段代码展示了如何为多个AGV依次规划路径，并在规划过程中考虑避障。每个AGV规划完路径后，将路径上的网格标记为障碍物，防止其他AGV再次经过。

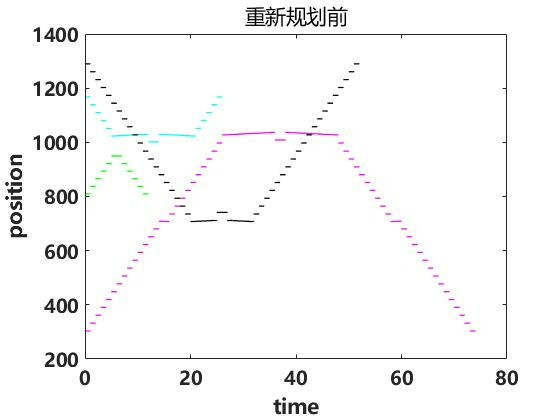
通过以上在Matlab环境下基于A星算法的多任务多AGV路径规划系统优化，我们可以有效解决仓库场景下多AGV自由移动中的避障和最短路规划问题，提升仓储物流的运作效率。当然，实际应用中还需要考虑更多的复杂因素，比如AGV的速度控制、实时动态环境变化等，这就有待我们进一步探索和优化啦。