自动潜航器的高效控制：修正C/GMRES算法探秘

用于自动潜航器快速非线性模型预测跟踪控制的修正 C/GMRES 算法-306

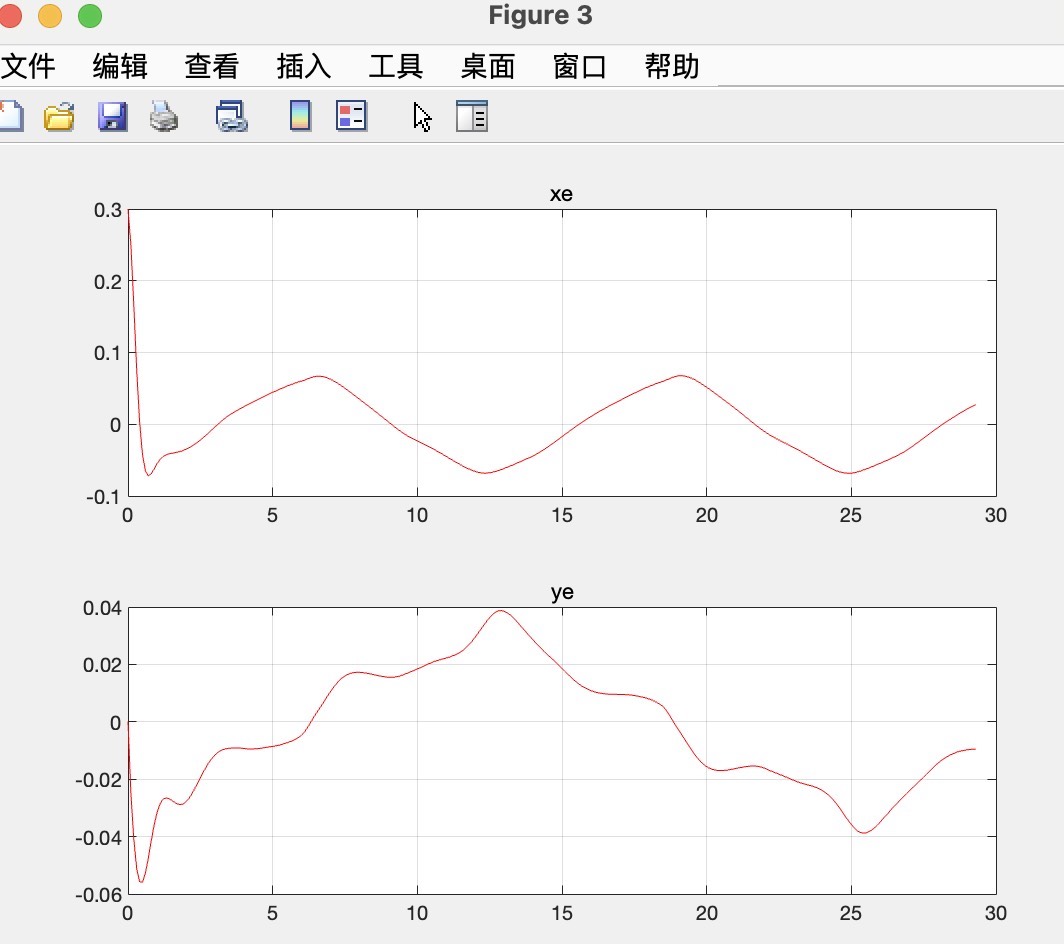
在自动潜航器（AUV）的控制领域，快速且精准的非线性模型预测跟踪控制至关重要。今天咱们就来深入聊聊用于此的修正C/GMRES算法。

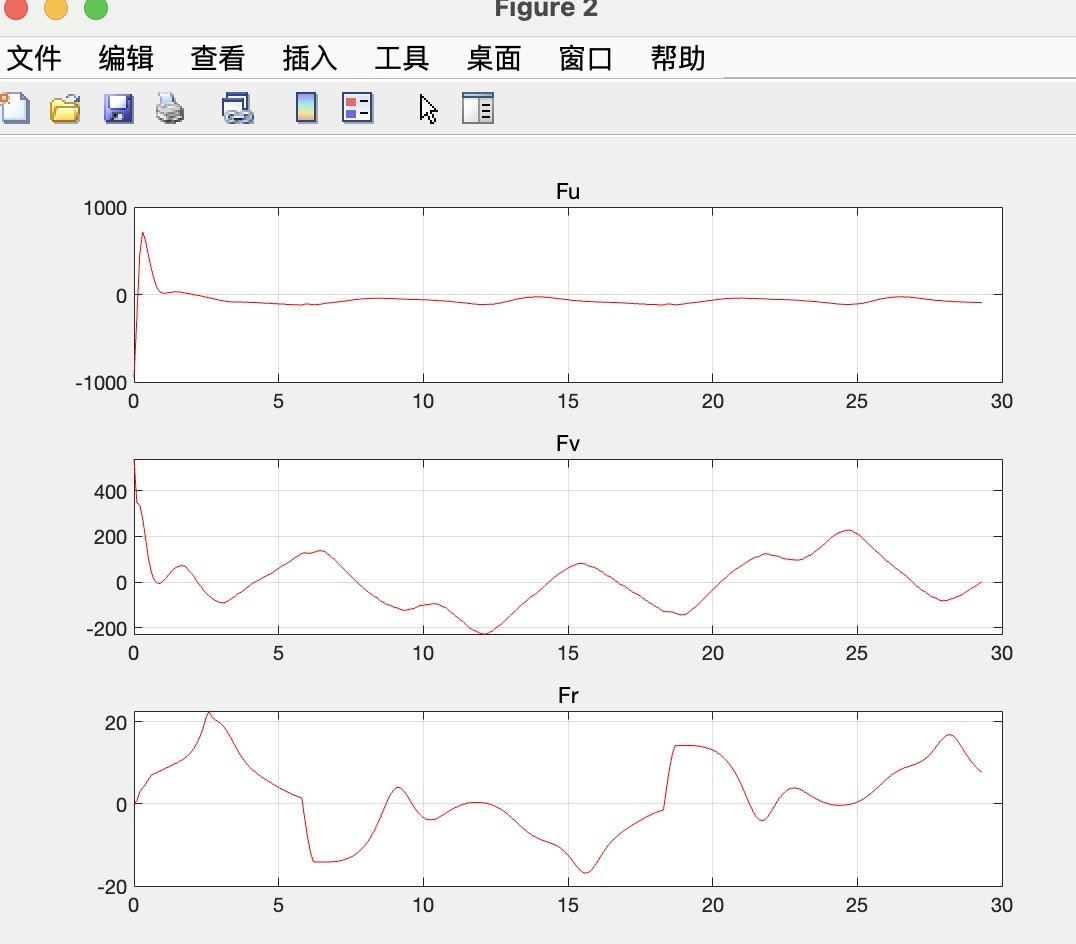
AUV在水下复杂环境中运行，其运动控制面临诸多挑战。非线性模型预测控制（NMPC）旨在通过对系统未来动态的预测，优化控制输入，以实现期望的轨迹跟踪。然而，传统算法在处理这类复杂的非线性优化问题时，计算量较大，效率难以满足实际应用需求，特别是在对实时性要求极高的AUV控制场景中。

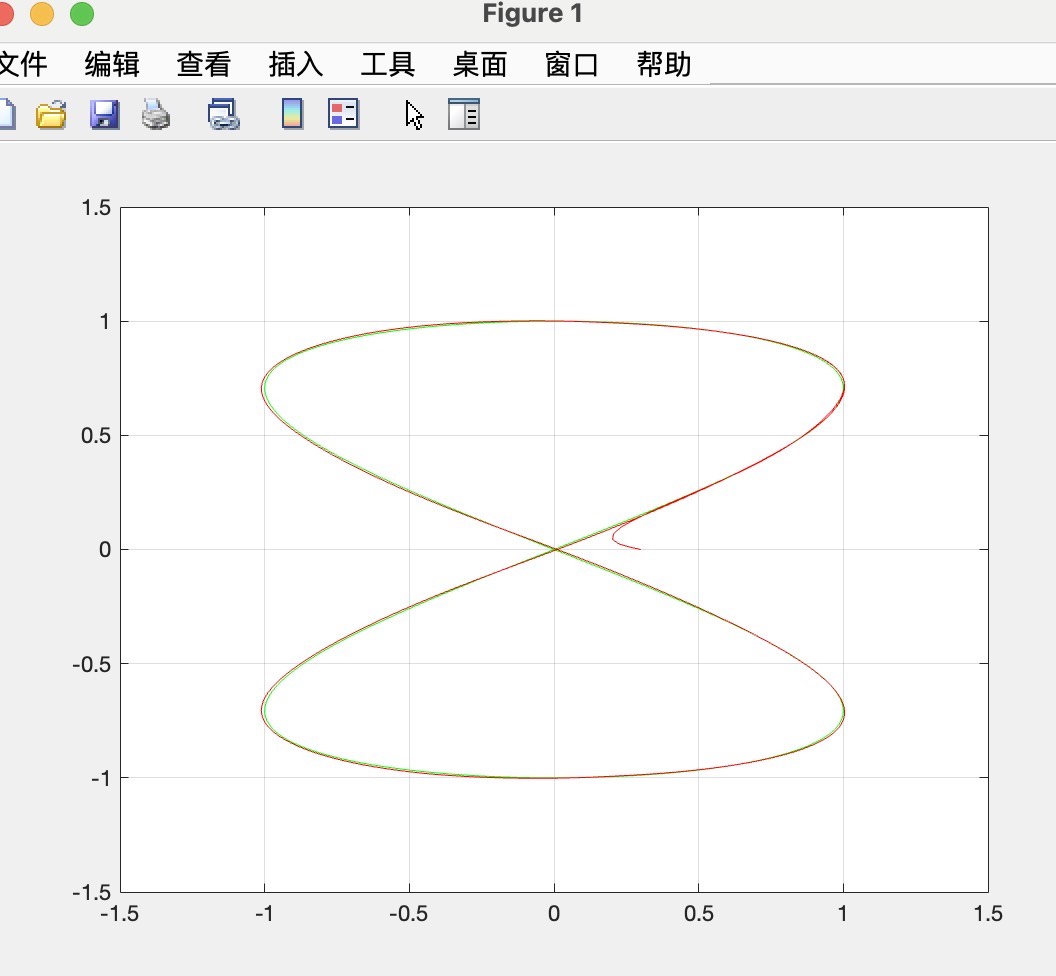
这时候，修正C/GMRES算法就闪亮登场啦。GMRES（广义极小残差法）原本是用于求解大型稀疏线性方程组的迭代方法。但在AUV的非线性模型预测跟踪控制场景下，对其进行修正以适应特定需求就显得尤为重要。

我们来看看简单的代码示例（这里以Python伪代码为例帮助理解，实际应用可能用更适合的语言和库）：

python 复制代码

import numpy as np


# 定义一些假设的系统参数
n = 100  # 假设的系统维度
A = np.random.rand(n, n)  # 系统矩阵
b = np.random.rand(n)  # 右侧向量


def gmres(A, b, max_iter=100, tol=1e - 6):
    m = len(b)
    x = np.zeros(m)
    r = b - np.dot(A, x)
    beta = np.linalg.norm(r)
    V = np.zeros((m, max_iter + 1))
    V[:, 0] = r / beta
    H = np.zeros((max_iter + 1, max_iter))
    for k in range(max_iter):
        w = np.dot(A, V[:, k])
        for j in range(k + 1):
            H[j, k] = np.dot(V[:, j].T, w)
            w = w - H[j, k] * V[:, j]
        H[k + 1, k] = np.linalg.norm(w)
        if H[k + 1, k] < tol:
            break
        V[:, k + 1] = w / H[k + 1, k]
    # 计算最小二乘解
    y = np.linalg.lstsq(H[:k + 2, :k + 1], beta * np.vstack((np.eye(k + 1), np.zeros((1, k + 1)))), rcond=None)[0]
    x = x + np.dot(V[:, :k + 1], y)
    return x


# 这里假设修正部分是对系统矩阵A进行预处理
def precondition_A(A):
    # 简单示例：这里可以是复杂的预处理操作，这里假设是取A的对角矩阵作为预处理器
    return np.diag(np.diag(A))


preconditioned_A = precondition_A(A)
solution = gmres(preconditioned_A, b)

在这段代码中，我们首先定义了一个基本的GMRES函数来求解线性方程组Ax = b。在AUV的应用场景里，这个方程组可能是由非线性预测模型离散化后得到的。而修正部分，我们通过precondition_A函数对系统矩阵A进行预处理，以加速GMRES的收敛速度。在实际的AUV控制中，预处理操作可能基于对AUV动力学模型的深入理解和分析，通过巧妙地构造预处理器，让GMRES算法在更少的迭代次数内达到收敛，从而满足快速控制的需求。

修正C/GMRES算法通过对传统GMRES算法的适应性改进，为AUV的非线性模型预测跟踪控制提供了更高效的解决方案，助力AUV在复杂水下环境中更加敏捷、精准地执行任务。它就像是给AUV装上了一个智能的"导航大脑"，在提升控制性能的同时，也为水下探索等相关领域的发展注入了新的活力。

希望通过今天的分享，大家对用于自动潜航器快速非线性模型预测跟踪控制的修正C/GMRES算法有了更直观的认识。后续有机会咱们可以继续深挖更多相关的有趣技术点。