目录
摘要
今天学习了K-means算法初始化和聚类数选择的关键问题。在初始化方面,我理解了随机选择k个训练样本作为初始聚类中心的方法,以及通过多次随机初始化来避免局部最优解的技巧。对于聚类数的选择,认识到这往往没有标准答案,需要根据数据特性和应用需求来判断。通过可视化不同k值下的聚类效果,我明白了肘部法则等选择聚类数的实用方法。
Abstract
Today's lesson focused on two crucial aspects of K-means algorithm: initialization and cluster number selection. For initialization, I learned the method of randomly selecting k training samples as initial centroids and the technique of multiple random initializations to avoid local optima. Regarding cluster number selection, I recognized that there's often no definitive answer, requiring judgment based on data characteristics and application needs. Through visualizing clustering effects under different k values, I understood practical methods like the elbow method for determining the optimal number of clusters.
一、初始化K-means
K-means聚类算法的第一步是选择随机位置作为初始猜测的K-聚类中心,并选择μ1到μk,但我们实际上如何进行这个随机猜测呢,以及如何对μ1到μk的初始猜测进行多次尝试,从而找到更好的聚类集合,让我们来看看
这里再次展示了K-means算法

在这个小节中,让我们看看如何实现第一步
运行K-means时,我们几乎总是应该选择聚类数k小于训练样本数m,当k>m时,那样会导致没有足够的训练样本来保证每个聚类中心至少有一个训练样本
为了选择聚类中心,最常见的方法是随机选择k个训练样本,所以这里有一个训练集,如果我们随机选择两个训练样本
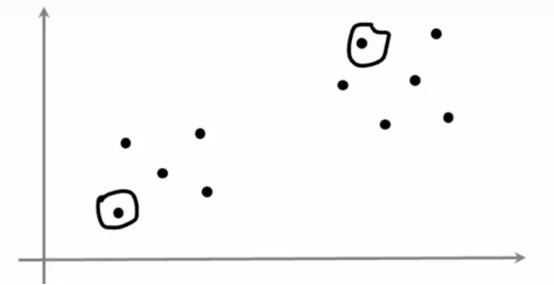
然后我们将μ1到μk设置为k个训练样本,所以我们可能会在这里初始化我们的红色聚类中心,并在这个例子中初始化我们的蓝色聚类中心
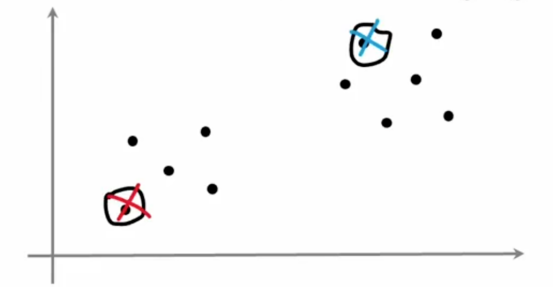
其中k = 2
事实证明,如果这是我们随机初始化并且我们运行K-means,我们会发现K-means决定这些是数据集中的两个聚类,请注意,这种初始化聚类中心的方法与我们在之前小节中的插图中使用的方法有所不同
在之前的视频中,我们将聚类中心μ1和μ2初始化为随机点,而不是位于特定的训练样本上,而这节中,我们会学习一种更常用的初始化聚类中心的方法,有可能我们会得到一个聚类中心的初始化,其中红色的交叉点在这里

根据我们选择随机初始聚类中心的方式,K-means最终会为我们的数据选择一个不同的聚类
让我们看一个更加复杂的例子,我们将查看这个数据集并尝试找到三个聚类,所以在这个数据中,k=3

如果我们用一个随机初始化的聚类中心运行K-means
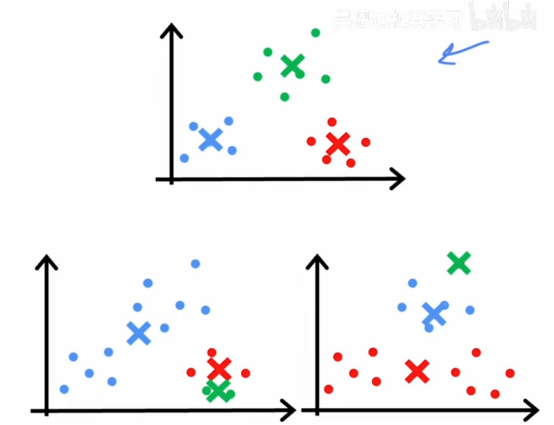
我们发现上面那个表现好像还不错,但如果我们使用不同的初始化,我们会得到不同的初始化结果,比如左下角的和右下角的结果,左下角的这个结果是一个局部最优解,K-means在尝试最小化失真成本函数,但如果随机初始化不太走运,也会导致右下角这个局部最小值的情况,这两个一打眼就知道没有上面那个表现好,所以如果我们想让K-means多次尝试找到最好的局部最优解,尝试多次随机初始化,以增加找到上面那个好聚类的机会,我们可以做的另一件事是多次运行K-means然后尝试找到最好的局部最优解
那么选择三个解决方案的一种方法是计算这三个解决方案的代价函数j,K-means找到的三个聚类方案中的所有这些选择,然后根据哪个给出最低的代价函数来选择这三个解决方法,事实上,如果我们看看上面的一组聚类,这个绿色叉号有相对较小的平方距离,红色叉号在红色点有相对较小的平方距离,同样蓝色叉号也是如此,所以说在这个例子中,代价函数j会相对较好,但是我们看到左下角这个例子,蓝色叉号到所有蓝色点的距离较大,右下角的红色叉号到所有红色点的距离较大,会导致很大的代价函数,这就是我们根据代价函数的大小来选择解决方案的途径
以上都是直观的理解,现在让我们更加正式地写出这个算法,我们会多次运行K-means使用不同的随机初始化,如果我们想为K-means使用100次随机初始化

二、选择聚类的个数
K-means算法需要输入参数k,但我们怎样才能知道该如何决定使用多少聚类呢?这就是我们这个小节需要讨论的问题
对于许多聚类问题,如果我们向不同的人展示同一个数据集,然后问他们你看到了多少个聚类
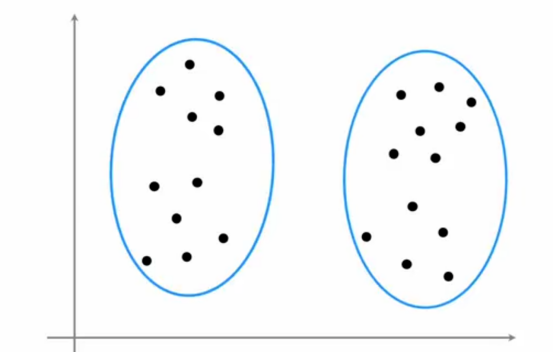
一定会有人说,我看到两个聚类,这是没问题的
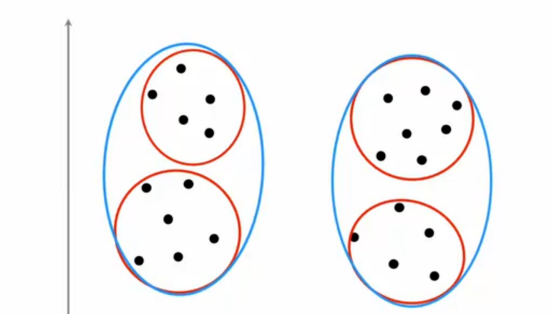
但是肯定也有人说,这肯定是四个聚类,这也是没毛病的,因为聚类是一种无监督的学习算法,所谓的正确答案是通过特定标签来复制的,因此在许多应用中,数据本身并没有明确指出有多少个聚类,在我看来,这个数据究竟是两个、四个还是三个聚类确实是模棱两可的
总结
今天的学习让我对K-means算法的实际应用有了更深入的理解。初始化不再是随便选几个点那么简单,而是要通过多次尝试来找到更好的聚类结果,这就像做实验时要重复多次取平均值一样重要。聚类数k的选择让我意识到机器学习中很多问题都没有唯一正确答案,需要结合具体场景来分析。肘部法则虽然简单但很实用,通过观察成本函数的变化趋势来做出相对合理的选择。这些知识让我明白,在实际应用中,算法参数的选择往往需要结合业务理解和多次实验,不能完全依赖自动化的方法。